Разработка модели разваривания зернового замеса

В технологии производства пищевого спирта важная роль принадлежит процессу разваривания зерна. Исследования ведутся в направлении изучения влияния степени измельчения, температур, ферментов и других способов воздействия на зерно и зерновые замесы. Можно отметить, что успехи в снижении энергозатрат и улучшении качества бражки достигнуты за счет снижения тем ператур при использовании гидродинамической ферментативной обработки (ГДФО) и механико-ферментативного разваривания. Научные исследования этих вопросов обобщаются в виде эмпирических соотношений и оптимизации технологических режимов [1]. Обобщающие эмпирические уравнения и теоретические обобщения экспериментального материала нуждаются в дальнейшем развитии. Обычно разваривание осуществляется в несколько стадий: смешения с водой при температурах 40-50 °С, в том числе с добавлением разжижающих ферментов, последующего по- вышения температуры и разваривания в две-три стадии. Поэтому при математическом описании этого процесса необходимо учитывать изменение температур и концентраций влаги в частичках материала. Диффузионное насыщение влагой частиц зерновой крупки может быть описано с использованием уравнений нестационарной диффузии и решено численным методом, разработанным нами для описания сушки барды [2]. В настоящей работе рассмотрена задача диффузионного разваривания зерновой крупки, которая учитывает процесс диффузии влаги в материале, кинетику набухания крах мальных гранул и переменную температуру.

Математичекое описание процесса осуществлялось с использованием уравнения нестационарной диффузии в частных производных (1):

д Cд

= D (t      ,(1)

дт где С - влажность материала, изменяющаяся во времени и в пространстве, м3 влаги/м3 влажного материала; т - время, с; x - коорди ната в направлении, перпендикулярном к слою, м; D(t) - коэффициент диффузии воды в материале, м2/с.

Влияние температуры на процесс учитывалось через коэффициент диффузии:

D ( t ) = D о d e — E ad / RT ,            (2)

где Dоd - предэкспоненциальный множитель (фактор диффузии); Ead - энергия активации для диффузии адсорбированной воды, Дж/моль; T - абсолютная температура, К; R - газовая постоянная, R = 8,314 Дж/(молыК); индекс d - диффузия.

Как следует из уравнения (2) с ростом температуры величина экспоненты быстро стремится к единице. Поэтому величина D о найдена нами по данным [3] путем экстраполяции. Величина D о составила 5,5-10 " ⁹ м²/с. Величина энергии активации найдена путем идентификации математической модели нестационарной диффузии E_ad = 21,75 кДж/моль [4].

Поскольку решение уравнения (2) проводилось численными методами, то по заданной в процессе разваривания крупки температуре как функции времени определялась температура на каждом временном слое интегрирования, и по ней рассчитывался коэффициент диффузии.

Решение уравнения нестационарной диффузии (1) осуществлялось методом сеток. Для исключения расходимости вычислений применена неявная схема (рисунок 1), изложенная в работе [5] и реализованная нами в [2].

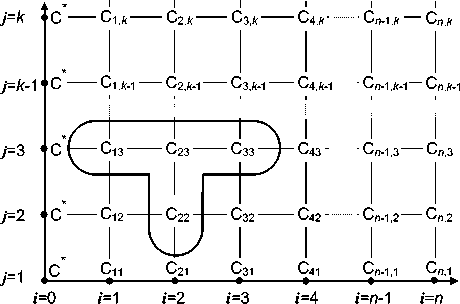
Рисунок 1. Трафарет неявной схемы

Через i обозначены слои по координате, через j - по времени. В узлах сетки располагаются значения влажности и температуры. Значения влажности на нижнем временном слое известны, на верхнем слое - подлежат определению. Полученная на каждом временном слое система линейных уравнений с трехдиагональной матрицей решалась методом последовательного исключения переменных.

Уравнение (1) в конечных разностях имеет вид:

C , j + 1 — C , j       С и j + 1 — С , j + 1Н С , j + 1 - С и j + 1 )

= Dt '          й •⁽³⁾

После преобразований получим:

- Fo - C - 1, j + 1 + ( 1 + 2Fo ) C , j + 1 - Fo - C + 1, j + 1 = C , j , (4)

где

D ( t ) At

Fo = Tv .           ⁽⁵⁾

Начальные условия: т = 0 C i ,1 = C ₀.

Учтем, что C 0, j = C и получим:

B ‘ C 1,2 + DC 2,2 = 8 1                          (10)

A 2 ^C 1,2 ^{+ B} 2 ^C 2,2 ⁺ D 2 ^C 3,2 = ⁸ 2             ⁽¹¹⁾

Граничные условия:

на границе соприкосновения с водой:

x = 0         C0, j = C *, в центре частицы:

- x ~          n n-1,j n,j,j , где С0 – начальная влажность крупки

( С ₀ = 0,194 об. дол. или 0,147 мас. дол.);

С ^* – равновесная концентрация влаги в твердом теле на границе раздела фаз (найдена при идентификации и составила 0,888 об. дол. или

0,85 мас. дол.); при x = — производная ^- = 0, 2              dx т.е. Cn-1,j = Cn,j .

Ниже представлен алгоритм решения системы линейных уравнений с трехдиагональной матрицей, получаемых при использовании неявной схемы при разбиении пространственной координаты на n участков и числе шагов интегрирования по времени равном k .

Для начального временного слоя ( j = 1) и второго слоя ( j = 2) при n шагах интегрирования по координате уравнение (4) принимает вид системы уравнений с трехдиагональной матрицей:

- Fo • C 0,2 + ( 1 + 2Fo ) C i,2 - Fo • C 2,2 = C^ (6) - Fo • C 1,2 + ( 1 + 2Fo ) C 2,2 - Fo C 3,2 = C 2,1 (7)

A n - 1 C n - 2,2 + B n - 1 C n - 1,2 + D n - 1 C n ,2 =8 n (12)

C n - 1,1 =8 n (13)

Решим систему (10)-(13) следующим образом.

Умножая каждое слагаемое уравнения (10) на A ₂ / B ₁ , получим (14):

AA

A 2 C1,2 + D1 T"C 2,2 =T81.

B1

Из уравнения (11) вычтем уравнение (14):

B 2 - D 1 A -) C 2,2 + D 2 C 3,2 = 8 2 - A - 8 1 . (15)

V       B1J

Обозначим:

B 2 = B 2 - D 1 A 2 ;    8 2 = 8 2 - A 2 8 1 . (16)

B1

С учетом выражений (16) уравнение (15) примет вид:

b 2 c2,2 + d 2 C3,2 = 82.(17)

После преобразований получена следующая система уравнений:

B‘C1,2 + D1C2,2 = 81;(18)

B 2 C2,2 + D 2 C3,2 =82;(19)

Bn-1Cn-1,2 + Dn-1Cn ,2 =8 n-1.(20)

Так как C_n - 1, ₂ = C_n , ₂, то из уравнения (20)

определена концентрация C_n - 1, ₂ , из уравнения

(19) – концентрация С _2,2 , из уравнения (18) –

- Fo ^ C n - 2,2 + ( 1 + 2Fo ) C n - 1,2 - Fo C n ,2 = C n - 1,1 (8)

C n - 1,1 = C n ,1 (9)

Строго говоря, на соседних временных слоях величины температур различны, а по-

D ( t ) ^Д т n этому различны и величины Fo = —    . Од-

( A x )

нако на соседних временных слоях температура отличается на 0,05 º С, и этим различием можно пренебречь. При переходе же на последующий слой осуществляется пересчет температуры и величины Fo .

Обозначим:

A i =- Fo; B i = ( 1 + 2Fo ) ; D =- Fo; 8 1 = C _u;

концентрация С _1,2 . Таким образом, из системы

уравнений (18)-(20) найдены концентрации на 2-м временном слое:

^Cn - 1,2

⁸ n - 1        .

B n - 1 + D n - 1 ’

^C 2,2 =

—

D 2 C 3,2

B 2

;

^C 1,2 =

—

D 1 C 2,2

B 1

.

Аналогичным путем осуществлен пере-

⁸ 2 = ^C 2,1 ;   ⁸ 3 = ^C 3,1 ; ... ⁸ n - 1 = ^Cn - 1,1 ;   ⁸ n = ^Cn ,1 ^;

8 1 = 8 1 - AC ; B ‘ = B 1 .

ход от второго слоя к третьему и т.д., вплоть до определения концентрации во всех узлах сетки. Распространяя полученный результат на i = 1... n - 2 и j = 2... k , имеем

r = 8i - DiCi+1,j i, j            Bi        ,

Для i = n и i = n - 1 имеем:

С 1

C n - 1, j

^£ n - 1        .

B n - 1 + D n -1’

• n , j ^П - 1, j •

Коэффициенты определены следующими уравнениями:

А

B i = B i - D - - i -,        (25)

B i - 1

где i = 2... n ; B ‘ = B 1 ; £‘ = £ 1 - A 1 C .

A

^£ i =^£ i ^- r' ^£ ‘ - 1 ,               ⁽²⁶⁾

B i - 1

где i = 2... n - 1.

По вышеизложенной методике определяются концентрации влаги C i , j в узлах сетки

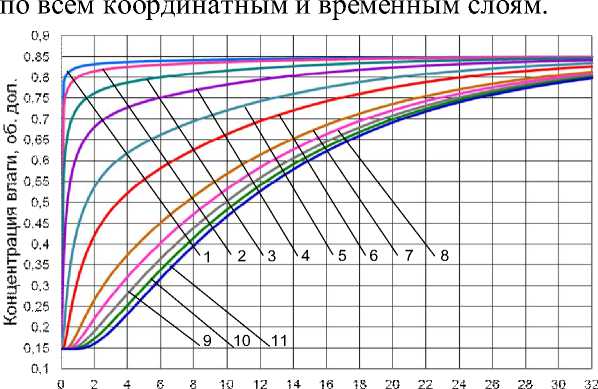
Продолжительность разваривания, ч

Номер слоя: 1 - 1; 2 - 2; 3 - 5; 4 - 10; 5 - 20;

6 - 30; 7 - 50; 8 - 60; 9 - 70; 10 - 80; 11 - 100

Рисунок 2. Расчет по диффузионной модели

Как видно из рисунка 2, концентрация влаги изменяется в пространстве и во времени. График построен при следующем температурном режиме: первые 30 минут температура равна 50 °С, от 30 до 50 минут температура изменялась от 50 до 70 °С со скоростью 1 °/мин и при времени, большем, чем 50 мин температура оставалась постоянной, равной 70 °С. Таким образом, чисто диффузионная модель, учитывающая изменение температуры, дает время разваривания крупки, имеющей толщину 1 мм, равное 32 ч, вто время как реальный процесс разваривания был завершен за 225 мин. С целью выявления причин существенного отклонения теоретических данных от экспериментальных был проведен эксперимент по развариванию при температуре 90 °С пшеничной крупки, полученной после дробилки и вальцов, размером порядка 1 мм. Частицы были замочены водой, температура которой 40 °С, суспензия быстро разогрета до 90 °С и выдержана при этой температуре в течение 1 часа. Под микроскопом были сфотографированы края сухой и разваренной частиц (рисунок 3).

Из рисунка 3 видно, что сухая частица состоит из крахмальных гранул, размер которых в пересчете на эквивалентный диаметр составил 18 мкм. После разваривания размер гранул увеличился до 31,4-31,45 мкм. В среднем при размере 31,42 гранулы разрывались и крайний крахмальный слой переходил в жидкую фазу. В соответствии с этой картиной разбухшая гранула в момент отрыва слоя имела концентрацию воды порядка 80 % мас.

твердой

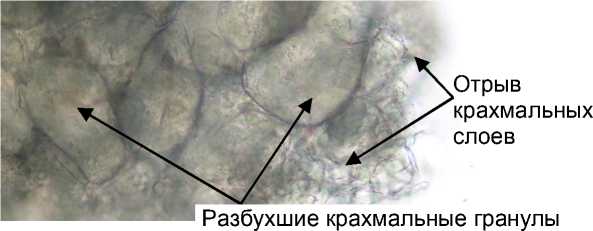
в твердой фазе

Рисунок 3. Внешний вид сухой и разваренной частиц крупки

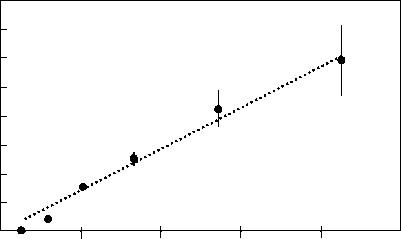
Для моделирования описанного процесса была рассмотрена теория набухания крахмальных гранул. По процессу набухания накоплен обширный экспериментальный материал, результаты которого обработаны с использованием модели химических реакций 1-го [6-8], 2-го [9-11] и 3-го [7] порядка. Экспериментальные результаты авторов вместе с собственными экспериментальными данными [9] обобщены в виде графика, представленного на рисунке 4.

На рисунке 4: D 0 — диаметр исходной (сухой) гранулы крахмала, мкм; D m — максимальный диаметр набухшей гранулы крахмала, мкм; D t — текущий диаметр гранулы крахмала (при набухании), мкм, V — предэкспоненци-альный множитель, с^-1 , E a — энергия активации, Дж/моль; R = 8,314 — универсальная газовая постоянная, Дж/(молыК); T — температура, К; т — время, с.

Q

6 Q

1·10-12    2·10-12     3·10-12   4·10-12   5·10-12

J exp k- RE w)'^T

Рисунок 4. Зависимость ( D t - D ₀ ) / ( D m - D t ) как

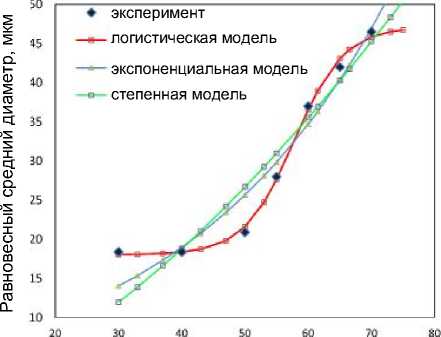
При низких температурах диаметр возрастает медленно, затем в диапазоне температур от 45 ºС до 65 ºС изменение диаметра происходит практически по прямой, а при более высоких температурах кривая асимптотически приближается к 40 мкм.

Обзор последующих работ по набуханию крахмальных гранул выполнен в работе [12]. Приведены данные по равновесному ср едн ему диаметру. Рекомендована сигмообразная модель для вычисления равновесного среднего диаметра [13]. На рисунке 6 представлены также расчеты по другим моделям [14-15], которые имеют большее отклонение от экспериментальных данных.

функция от J

exp

—

k

E a

RT ( t )

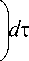
По этим данным определена величина энергии активации реакции набухания крахмальных гранул E a = 84,8 кДж/моль, и множитель V ₀ , равный 2,84·1012 с^-1. В р езультате

получено уравнение [9]:

D t — D о

D m - D t

V о J exp RTTyd'

Из уравнения (27) найдена величина D_t

Температура, ºС

Рисунок 6. Изменение равновесного среднего диаметра крахмальной гранулы в зависимости от температуры

^D 0 + D m

D t =--------- ^:

1 + V о

V 0

!T

.

По уравнению (28) путем численного интегрирования проведен расчет зависимости диаметра крахмальной гранулы от температуры. Температура изменялась от 20 ºС до 120 ºС со скоростью 1 ºС/с. Результаты представлены на рисунке 5.

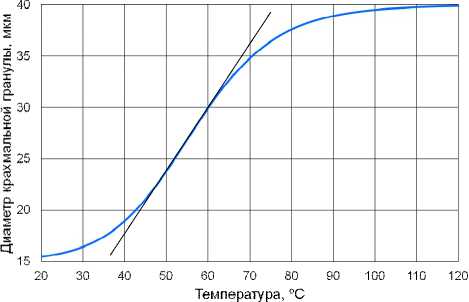
Рисунок 5. Изменение диаметра крахмальной гранулы в зависимости от температуры

В связи с тем, что по результатам работы [9] получается качественно такая же зависимость, как и представленная на рисунке 6, в дальнейшем для моделирования процесса набухания крахмальных гранул использовано уравнение (28).

В качестве экспериментальных данных для моделирования взяты результаты работы [16] по развариванию ячменной крупки. В эксперименте [16] проводилось разваривание в соответствии с температурным режимом, представленным при построении зависимостей на рисунке 2.

Процесс диффузионного насыщения протекает одновременно с процессом набухания гранул. Расчет должен проводиться по лимитирующему, т.е. более медленному, процессу. При математическом моделировании была использована сетка с 4800 слоями по времени и 100 слоями по координате.

Сначала была рассчитана кинетика набухания гранул. Время до разрыва крахмальных гранул и отрыва крахмального слоя оказалось равным 40 мин. Аналогичное время для диффузионного процесса оказалось рав -ным 24,5 мин. Так как эти процессы идут независимо друг от друга, то вплоть до времени 40 мин расчет проводился по набуханию. В это время 2-й слой насыщался до концентрации влаги, равной 75 % мас. После отрыва 1-го слоя начинался более быстрый рост концен- дели полное разваривание частичек материала произошло за время 225 мин, что согласуется с

Номер слоя: 1 – 1; 2 – 2; 3 – 5; 4 – 10; 5 – 20; 6 – 30; 7 – 540; 8 – 50; 9 – 60; 10 – 70; 11 – 80; 12 – 90; 13 – 100

Рисунок 7. Расчет по разработанной модели

Таким образом, разработана модель разваривания зернового замеса, учитывающая разрыв крахмальных гранул при набухании и отрыв слоя, граничащего с жидкой фазой, до