Разработка модуля оптимизации рецептур продовольственных продуктов в составе автоматизирован-ной информационной системы

Постоянное обновление ассортимента продовольственных продуктов, растущая потребность в продуктах функционального назначения, разнообразие предложений на рынке сырьевых ингредиентов актуализируют вопросы проектирования новых рецептур продовольственных продуктов, их оперативной коррекции в зависимости от колебаний параметров сырья, требований к функциональности продуктов питания и конъюнктуры рынка.

В разработанной авторами автоматизированной информационной системе (АИС) предусм отрены следующие возможности : работа с базой данных пищевых ингредиентов; эволюция процедурных моделей; оптимизация рецептур продуктов питания по сов окупности заданных критериев; формирование результатов расчета в форме стандартных отчетов [1].

При разработке АИС использовался объектно-ориентированный подход, основным достоинством которого является возможность наследования свойств и методов расчета, что связано с возможностью добавления новых формул в процессе эволюции процедурных моделей [2]. В частности, может быть поставлена и решена задача проектирования состава

Толстых С.Г., Толстых С.С., 2013

сложных многокомпонентных пищевых систем с заданными характеристиками в условиях множества альтернатив ингредиентного состава и взаимозаменяемости сырья с допустимым (или минимальным) уровнем себестоимости.

АИС состоит из трех модулей: информационного, расчетного и оптимизации. Информационный модуль включает совокупность данных о компонентах и полуфабрикатах рецептур. В расчетном модуле осуществляется выборка и коррекция исходных данных, производятся расчеты продовольственных продуктов со сложным сырьевым составом, а также пищевой, биологической и энергетической ценности этих продуктов. В модуле оптимизации производится подбор компонентов рецептуры по совокупности критериев пищевой, биологической и энергетической ценности, а также себестоимости продукта.

Описание структуры информационного и расчетного модулей, используемых алгоритмов, программного обеспечения, предназначенного для расчета рецептур со сложным сырьевым составом, изложено в наших работах [1-4]. В данной статье формулируется задача многокритериальной оптимизации рецептуры продовольственных продуктов, описаны алгоритм ее решения и структура модуля оптимизации в составе АИС.

Далее представлена постановка задачи оптимизации рецептур продовольственных продуктов.

Пусть нам известен набор альтернативных вариантов сырьевых ингредиентов и эскизная технологическая схема (основные стадии) производства нового продукта питания (готового продукта). Требуется определить рецептуру x = ( x 1 ,x ₂,.... x n ) готового продукта, при которой основные потребительские характеристики (пищевая, биологическая, энергетическая ценность и др.) и себестоимость готового продукта F ( x ) = ( f . ( x ), f >  ( x ),..., f m ( x )) достигают оптимальных значений, а другие потребительские характеристики (например, микробиологические показатели, срок хранения и т.п.) g j ( x ) , j = 1, r удовлетворяют требованиям технического задания на разработку рецептуры нового продукта питания, т.е. g j ( x ) <  0, j = 1, r .

Математическая постановка задачи проектирования оптимальной рецептуры имеет следующий вид:

x * = argmin{ F ( x )},              (1)

x e X                           ^{v 7}

при связях в форме иерархической модели продукта питания со сложным сырьевым составом (рисунок 1).

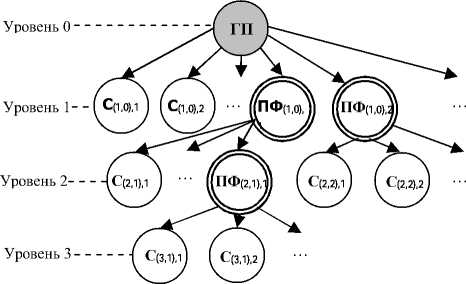
Рисунок 1 - Иерархическая структура рецептуры пищевого продукта (ГП - готовый продукт; С - сырьевой ингредиент; ПФ - полуфабрикат; нижние индексы - номера иерархическим уровней).

и ограничениях на другие потребительские характеристики готового продукта:

g j ^{( x )} <  ⁰, ^j = 1» ^r ,                  (2)

и соотношения сырьевых ингредиентов и полуфабрикатов:

x < x < x, i = 1, n .               (3)

Поясним индексы на рисунке 1, где показана трехуровневая иерархическая модель сложного пищевого продукта. В этой модели нумерация сырьевых компонент и полупродуктов ведется отдельно на каждом уровне. Готовый продукт имеет индекс 0. Индексация ингредиентов представлена в виде (i,j),k, где i - номер иерархического уровня; j - номер полуфабриката; k - номер ингредиента.

Сформулированная задача относится к классу многокритериальных задач линейного или нелинейного программирования. Поставленную задачу предлагается решать на основе максимально-информативного представления искомой области компромиссных решений точками, заполняющими параллелепипед (3) по методике И. М. Соболя. [5]. Изложим алгоритм решения задачи (1)-(3).

Шаг 1 . Формирование допустимой области D рецептурных ингредиентов.

Заполнение n -мерного параллелепипеда (3) осуществляется путем генерирования точек LP _T - последовательности по формуле:

x ( k ) = x ⁽ k F + ^ ( i , k ) ( x i — x i ) , i = 1, n , k = 1, N , где k - число точек k = 1, N ; i - координата k - ой                                точки;

^ (i, j ) = £ 2k-1 Г1 £| 2 fj 2-1 ] II 2 Г R 2-( 1+1-k)! | k=1         21=kL 1          1 J L i j               i J

L'J, F'l - соответственно, целая и дробная части вещественного числа; R - целочислен-jl ные табличные значения, числа Соболя И.М.; Р =1 + Llog2j J .

Для каждой сгенерированной точки x ^{( k} ) параллелепипеда (3) осуществляется проверка ограничений на потребительские характеристики готового продукта: g j ( x ^{( k} ) ) <  0, j = 1, r . Если все r условий выполнены, точка считается допустимой, т.е. она принадлежит области D . На рисунке 2 показаны точки LP _T -последовательности в проекции на плоскость x i ® x j e R .

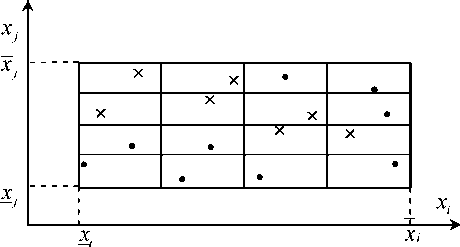
Рисунок 2 - Точки LP _T - последовательности: х — точки, принадлежащие допустимой области D.

Шаг 2. Расчет основных потребительских характеристик и себестоимости (критериев оптимизации) функционального продукта питания.

Для каждой точки области D осуществляется расчет основных потребительских характеристик и себестоимости. При этом фор- мируется множество точек в критериальном пространстве {f (x(k)), k = 1, ND}, где ND - чис ло допустимых точек в LPT - последователь- ности.

Шаг 3. Формирование области Парето Q .

Производится попарное сравнение всех допустимых точек из области D по значениям критериев путем проверки выполнения условий:

^{3 v:} f V ( x ^{( k 1 )} ) < ^f v ( x ^{( k 2 )} ) ,^v = 1, m ; k i = 1, N D ;

k ₂ = 1, N D ; k 1 A k ₂;

3 u : f„ ( x ^{( k 1} ) ) > f ( x ^{( k 2 )} ) aV h A u : f_h ( x ^{( k 1 )}) >  f_h ( x ⁽ k ² ) ), (5) u , h = 1, m ; k 1 = 1, ND ; k ₂ = 1, ND ; k 1 A k ₂.

Если условие (4) выполняется, точка x ^{( k 1 )} остается до следующей пров ерки в циклах по k 1 и k ₂, условие (5) не проверяется. Если не найдется такого v, при котором выполняется (4), производится проверка условия (5) и, если оно выполняется, точка x ^{( k 1 )} помечается как «бесперспективная» и не участвует в дальнейших сравнениях в циклах по k 1 и k ₂. B результате, после отбрасывания всех точек, помеченных как «бесперспективные», в области D остаются только те точки, которые принадлежат области Парето Q .

Шаг 4. Окончательное решение из множества эффективных точек Парето выбирается в зависимости от дополнительной информации (например, функциональности продукта питания, органолептической оценки готового продукта, конъюнктуры рынка и т.д.).

Далее дано описание модуля оптимизации рецептур. Модуль оптимизации состоит из двух блоков: блока исходных данных и расчетного блока. Первый блок формируется интерактивно, второй методологически поддерживается на уровне библиотеки классов, созданных для решения поставленной задачи. B блоке исходных данных интерактивно задается вся необходимая информация для решаемой задачи, а в расчетном блоке с использованием алгоритма решения задач (1)(3) осуществляется вывод на экран эффективных точек множества Парето, анализ которых позволяет эксперту сделать выбор окончательного решения. Интерфейс программы представлен на рисунке 3.

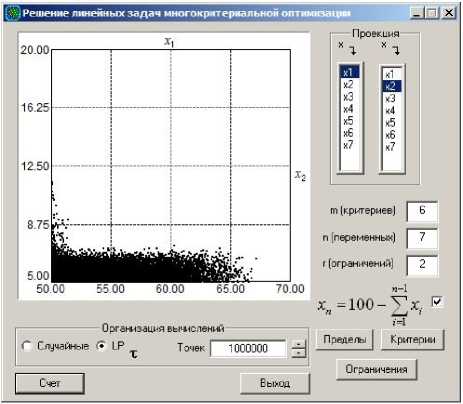
Рисунок 3 - Интерфейс модуля оптимизации

Для запуска модуля оптимизации АИС пользователь должен задать исходные данные и выбрать метод решения задачи оптимизации рецептур из числа методов, включенных в модуль оптимизации АИС. Далее он нажимает кнопку «Пуск» и через некоторое время получает проекции области Парето на экране. После окончания расчета для эксперта формируется специальный файл, где содержатся все расчетные данные, необходимые для принятия окончательного решения.

Приведем примеры решения задач оптимизации рецептур продовольственных продуктов.

1. Задача оптимизации рецептуры пастообразных продуктов на основе меда по пяти критериям ( f ( x ) - себестоимость готового продукта, f , ( x ) - энергетическая ценность, f ₃ ( x ) - содержание витаминов, f ₄ ( x ) - содержание макроэлементов, f ₅ ( x ) - содержание микроэлементов). Набор рецептурных ингредиентов и их характеристики представлены в таблице 1.

Таблица 1

Данные о рецептурных ингредиентах медовых паст

Наименование сырья, область допустимых значений, %	Содержание				Энергетическая ценность, ккал	Стоимость, руб.
	Сухие вещества, %	Витамины, мг	Макроэлементы, мг	Микроэлементы, мг
1. Ядро арахиса, 0-25	92,1	102,7	1289,0	11,3	127	60
2. Семена тыквы, 0-25	93,0	68,0	2577,0	25,4	541	190
3. Чернослив, 0-15	75,0	8,2	1139,0	3,0	256	110
4. Курага, 0-15	80,0	20,8	2015,0	3,2	232	90
5. Мед, 50-90	82,6	2,8	101,0	1,3	328	150

Целевые функции вычисляются по фор

мулам:

^fi ( x ) = 2 c j x j ⁺ c i,5

j = 1

(

100 - 2 x j

V         j = 1

, i = 1,6 ,

где Xj, j = 1,4 - процентное содержание ядер арахиса, семян тыквы, чернослива, кураги, соответственно; cx j, j = 1,5 - закупочные цены на ингредиенты медовой пасты, руб.; c2j , j = 1,5 — энергетическая ценность состав ляющих продукта, ккал; c3 j, j = 1,5 - содер жание витаминов, мг; c4j, j = 1,5 - содержание макроэлементов, мг; c5j, j = 1,5 - содержание микроэлементов, мг.

В результате решения многокритериальной задачи оптимизации (1)-(3) с ограничениями на содержание ингредиентов в рецептуре и сухих веществ было определено множество эффективных точек, принадлежащих области Парето, из которых выбиралось окончательное решение путем привлечения дополнительной информации. Варианты рецептур из множества оптимальных точек по Парето представлены ниже:

• 1)    Х = (24,38; 0,31; 9,92; 14,97; 50,42)

F = (115,24; 258,16; 30,58; 787,71; 4,27)

• 2)    Х = (24,6; 0,04; 11,54; 13,33; 50,49)

F = (115,27; 257,55; 30,42; 769,2; 4,22)

• 3)    Х = (24,98; 10,17; 13,75; 1,04; 50,24)

F = (125,46; 288,55; 35,32; 812,27; 6,5)

• 4)    Х = (5,21; 24,9; 5,14; 14,75; 50)

F = (144,36; 352,69; 27,17; 1115,02; 8,19)

• 5)    X = (9,53; 24,63; 13,48; 1,95; 50,41)

• 2.    Задача оптимизации печеночного паштета, набор рецептурных ингредиентов которого представлен в таблице 2, по шести критериям ( f ( x ) - себестоимость готового

F = (144,71; 349,73; 29,46; 1001,54; 8,46)

Окончательный выбор рецептуры из вышеприведенных вариантов производили, исходя из соотношения цена - качество с уче том органолептической оценки продукта. В данном случае можно предположить, что производитель, скорее всего, отбросит варианты рецептур с максимальным содержанием макро- и микроэлементов, себестоимость которых значительно выше (более чем на 25 %) рецептуры с минимальной себестоимостью, и выберет вариант рецептуры пасты с максимальным содержанием витаминов - х= (24,98; 10,17; 13,75; 1,04; 50,24); F*= (125,46; 288,55; 35,32; 812,27; 6,5).

продукта, f, (x) - энергетическая ценность, f3 (x) - содержание витаминов, f4 (x) - со держание макроэлементов, f5 (x) - содержа ние микроэлементов, f 6(x) - содержание не заменимых аминокислот).

Целевые функции вычисляются по фор- мулам:

f i ^{( x )} = 2 ^cij x j + ^ci7

j = 1

100 - 2 x j , i

V         j ^{= 1} J

= 1,6 ,

где Xj j = 1,6 - процентное содержание печени говяжьей, масла сливочного, молока сухого, белка сухого, яичного желтка, лука репчатого, соответственно; c1j, j = 1,7 - закупочные цены на ингредиенты паштета, руб.; c2j, j = 1,7 -энергетическая ценность составляющих продукта, ккал; c3 j, j = 1,7 - содержание витами нов, мг; c4j, j = 1,7 - содержание макроэлементов, мг; c5j., j = 1,7 - содержание микро элементов, мг; c6 j, j = 1,7 - содержание незаменимых аминокислот, г.

Т а б л и ц а 2

Данные о рецептурных ингредиентах печеного паштета

Наименование сырья, область допустимых значений, % Содержание Энергетическая ценность, ккал Стоимость, руб. Сухие вещества, % Жир, г Витамины, мг Макроэлементы, мг Микроэлементы, мг Незаменимые аминокислоты, г 1. Печень говяжья, 40-70 28,3 17,9 722,0 1061 16,5 8,1 127 150 2. Масло сливочное, 5-20 84,0 82,5 2,3 53 0,3 0,2 748 90 3.Молоко сухое, 5-10 96,0 1,0 38,9 4040 1,5 14,2 361 125 4.Яичный желток, 5-10 92,5 52,2 814,0 2002 15,6 6,6 612 160 5. Белок соевый, 0-20 94,5 0,8 0 2 0 21,8 338 86 6. Мука пшеничная, 0-20 96,0 1,8 102,5 460 10,6 33,0 324 10 6. Лук репчатый, 1-3 14,0 0,2 11,1 372 1,9 0,2 41 20 7. Вода, 0-10 0 0 0 0 0 0 0 0,1 та, f ,(x) - энергетическая ценность, f3 (x)-

В результате решения многокритериальной задачи оптимизации (1)-(3) с ограничениями на содержание ингредиентов в рецептуре, влаги и жира были определены эффективные точки области Парето. Варианты рецептур из множества оптимальных точек по Парето представлены ниже:

1) x = (57,29;6,21;5,15;6,71;0,17;12,27; 2,64; 9,56)

F = (129,89; 262,12; 470,39; 953,96; 10,6; 11,2) 2) Х = (69,89; 5,11; 7,29; 5,12; 3,6; 0,79; 2,02; 6,18)

F = (137,56; 227,2; 549,22; 1141,28; 12,45; 9,79) 3) Х = (69,99; 9,8; 5,87; 9,79; 0,75; 0,85; 2,39; 0,56)

F = (140,72;258,68;587,51; 1180,82; 13,19;8,16) 4) Х = (69,27; 5,51; 9,9; 8,97; 1,77; 0,89; 1,94; 1,75)

F = (141,05; 241,29; 577,09; 1317,51; 12,99; 9) 5) X =(60,12; 5,33; 5,13; 5,12; 4,61; 8,35;1,58; 9,76)

F = (248,23; 477,85; 951,07; 10,81; 11,24)

Поскольку оптимальные по каждому из заданных критериев рецептуры печеночного паштета незначительно отличаются по биологической и энергетической ценности можно рекомендовать вариант с минимальной себестоимостью готового продукта - x = (57,29;6,21;5,15; 6,71;0,17;12,27; 2,64; 9,56), F * = (129,89; 262,12; 470,39; 953,96; 10,6; 11,2)

• 3.    Задача оптимизации плавленого сыра с растительным наполнителем по пяти критериям ( f ( x ) - себестоимость готового продук

содержание витаминов, f4 (x)- содержание макроэлементов, f5 (x) - содержание микро элементов). Набор рецептурных ингредиентов и их характеристики представлены в таблице 3.

Целевые функции вычисляются по фор- мулам:

ft ^{( x )} = £ c j x j + c i ,8

j = 1

100 - £ x j

<          ^j = i >

i = 1,5,

где Xj j = 1,7 - процентное содержание брынзы, растительного жира, тыквенного пюре, сахара, соли-плавителя, молока сухого и воды, соответственно; c1 j, j = 1,8 - закупочные цены на ингредиенты сыра, руб.; c2j, j = 1,8 - энергетическая ценность составляющих продукта, ккал; c3 j, j = 1,8 - содержание витаминов, мг;

c ₄ j -, j = 1,8 - содержание макроэлементов, мг;

c₅ j , j = 1,8 - содержание микроэлементов, мг.

В результате решения многокритериальной задачи оптимизации (1)-(3) с ограничениями на содержание ингредиентов в рецептуре, сухих веществ и жира были определены эффективные точки области Парето, из которых экспертом было выбрано окончательное решение.

Т а б л и ц а 3

Данные о рецептурных ингредиентах плавленого сыра с растительным наполнителем

Наименование сырья, область допустимых значений, %	Содержание					Энергетическая ценность, ккал	Стоимость, руб.
	Сухие вещества, %	Жир, г	Витамины, мг	Макроэлементы, мг	Микроэлементы, мг
1	2	3	4	5	6	7	8
1. Брынза, 20 - 30	48	40	7,1	2545	0,7	262	170
2. Растительный жир, 0-15	100	100	0	0	0	898	40

Продолжение табл. 3

1	2	3	4	5	6	7	8
3. Тыквенное пюре, 20-30	14	0	11,9	309	0,9	22	60
4. Сахар, 15-30	100	0	0	0	0	399	27
5. Крахмал картофельный, 1-2	80	0	0	138	0	313	20
6. Соль-плавитель, 2-2,5	100	0	0	0	0	0	50
7. Молоко сухое, 0-10	96	1	38,9	4040	1,5	361	125
8. Вода, 10-20	0	0	0	0	0	0	0,1

Варианты рецептур, оптимальных по каждому из заявленных критериев, представлены ниже:

• 1)    x ˆ =(20,08;12,29;20,11;17,13;1,67;2,17;8,29;18,2) F ^ˆ = (61,82; 330,85; 3,82; 615,13; 0,32)

• 2)    x ˆ=(29,82;8,13;29,8;16,05;1,72;2,11;0,01;12,3) F ^ˆ = (79,39; 272,43; 5,66; 873,26; 0,48)

• 3)    x ˆ=(29,87;8,37;29,82;15,01;1,31;2,05;2,95;10,62) F ^ˆ = (79,45; 272,88; 5,67; 875,59; 0,48)

При решении задачи оптимизации плавленого сыра с растительным наполнителем получаем две близкие по составу рецептуры, удовлетворяющие четырем из пяти заданных критериев, однако с высокой (на 28,5 % выше минимальной) себестоимостью. В этом случае целесообразен выбор компромиссных вариантов рецептур из области Парето, например, следующего варианта рецептуры: x* =(20,04;12,94; 25,2;17,67;1,29; 2,16;1,94;8,76), F* = (63,96; 320,35; 5,42; 621,14; 0,37). В этом случае себестоимость сырного продукта вырастет незначительно – на 3,5%, а содержание витаминов будет близко к максимальному.

В заключение можно сказать, что разработанная АИС позволяет проектировать рецептуры продовольственных продуктов со сложным сырьевым составом с заданной пищевой, биологической и энергетической ценностью с учетом себестоимости готового продукта. Модуль оптимизации рецептур можно использовать также для создания функциональных продуктов питания, отвечающих физиологическим потребностям конкретных групп населения.