Разработка трехмерных моделей для учебно-тренировочных средств космического комплекса

толок а.в.

бронников С.в.

павлов д.в.

кузин С.а.

разумовСкий а.и.

ромакин в.а.

локтев м.а.

плакСин а.м.

В учебно-тренировочных средствах (УТС) космических комплексов (КК) [1] широко используются трехмерные модели внешнего вида и внутреннего интерьера космических аппаратов (КА) [2, 3] в целом, а также их элементов. К УТС относятся технические средства обучения, предназначенные для изучения устройства, принципа действия и правил эксплуатации КА, а также предназначенные для формирования, поддержания и совершенствования у персонала управления КК навыков эксплуатации КА [4].

Модели для УТС разрабатываются на основе конструкторской документации, которая создается с использованием систем разработки конструкторской документации ( CAD –систем) [5].

Модель КА в CAD –формате не может использоваться в УТС КК в реальном масштабе времени. Для этой цели необходима полигональная модель КА, позволяющая, например, реализовать качественное освещение с учетом движения КА по орбите, производить сложное текстурирование и выполнять анимирование элементов модели.

Полигональные модели могут быть получены путем трансляции имеющейся CAD–модели КА в формат пакета для 3D–моделирования (например, Autodesk 3ds Max) путем автоматического экспорта из CAD–системы [6]. Однако, характеристики быстродействия современных персональных компьютеров, используемых для создания УТС, либо не позволяют обеспечить визуализацию модели КА при моделировании в реальном масштабе времени в связи с большим количеством полигонов, либо, если увеличить сжатие модели при ее экспорте из CAD– формата в полигональную модель для уменьшения количества полигонов, изображения ряда важных для функционирования УТС элементов КА получаются слишком грубыми, неудовлетворительными [7].

Основным вариантом формирования трехмерной модели для УТС является разработка полученной полигональной модели вручную в пакете для трехмерного моделирования. При этом разработчик вручную создает модель, используя CAD –модель для формирования представления и определения размеров элементов КА.

Невозможность автоматического преобразования CAD –модели КА в полигональную связано с тем, что КА состоит из большого количества разномасштабных элементов, которые имеют различную значимость для задач УТС. Имеются элементы, которые требуется воспроизвести в УТС с высокой точностью (например, мишень для выполнения ручной стыковки). Имеются также элементы, которые персонал КК не использует в процессе управления полетом КА, и которыми можно пренебречь.

Поэтому для автоматизированного получения трехмерных моделей для УТС КК является актуальным создание программного обеспечения, которое позволяет в интерактивном и итеративном режимах управлять процессом преобразования трехмерной модели КА из формата CAD в полигональную форму с возможностью выбора различной степени автоматического уменьшения количества полигонов для каждого элемента трехмерной модели КА. В настоящее время аналоги подобного программного обеспечения отсутствуют.

Постановка задачи: разработать систему адаптации графического пакета (САГП), позволяющую сократить количество полигонов в отображаемом объекте с учетом обеспечения требуемой степени визуального подобия модели КА и каждого ее элемента.

САГП предназначена для загрузки в автоматизированном режиме полигональной трехмерной модели КА в формате VRML (подготовленной в PTC Creo ), проведения необходимых операций по упрощению отдельных элементов модели КА и последующего конвертирования в формат VRML пакета Autodesk 3ds Max .

САГП при преобразовании модели должна обеспечить:

• •    сохранение структуры трехмерной модели;

• •    инструмент управления элементами структуры модели;

• •    управление процентом количества сокращаемых полигонов (уменьшение количества полигонов в заданной пропорции во всей модели или в указанном ее элементе).

В технологию создания трехмерной модели КА для УТС, описанную выше, вводится дополнительная операция «автоматизированная адаптация графического пакета». Эта операция предшествует операции «доработка трехмерной модели вручную».

В настоящее время трехмерная модель для УТС разрабатывается вручную. При этом CAD –модель, а также фотографии КА используются в качестве исходных данных для получения размеров, внешнего вида КА и его составных частей.

Технологию ( Т ) для создания трехмерной модели для УТС формально можно представить в виде двух процессов:

T = {A , M}, где A — получение CAD–модели, фотографий КА; M — процесс ручной разработки модели.

При этом основное и значительное время занимает именно процесс ( M ), требующий кропотливой переработки основной геометрической информации и ручного труда по вводу данных и созданию модели.

С применением САГП предлагается дополнить технологию создания трехмерной модели инструментом адаптации модели КА:

T = { A , X , [ P_in , S_a , S_h , P_out ], M ′}, где A — получение CAD –модели, фотографий КА; X — экспорт CAD –модели в VRML –формат; [ P_in , S_a , S_h, P_out ] — подтехнология САГП (здесь P_in — преобразование формата VRML в формат САГП; S_a — автоматизированный процесс сокращения количества полигонов; S_h — ручное удаление выбранных полигонов; P_out — преобразование формата САГП в VRML –формат); M ′— ручная доработка трехмерной модели.

Предложенная технология не исключает процесса ручной доработки модели на стадии построения УТС, однако трудоемкость процесса M ′ существенно меньше, чем трудоемкость процесса M .

САГП предназначена для расширения средств по применению компьютерной конструкторской документации, создаваемой в PTC Creo [8] для задач построения УТС, где выдвигается требование к структурно управляемому сокращению количества элементов сетки в отображаемом объекте с учетом сохранения его визуального восприятия.

Комплексный подход САГП заключается в организации взаимодействия двух систем: PTC Creo и 3ds Max [3], так как создание исходной конструкторской модели средствами PTC Creo и моделей для УТС средствами 3ds Max осуществляется различными группами специалистов. Попытки организации взаимодействия перечисленных систем на уровне открытых файлов ожидаемых результатов не дают, что приводит к множеству операторных вмешательств в подготовку входных данных.

Эскиз планируемой архитектуры проекта системы адаптации графического пакета представлен на рис. 1.

Центральным элементом САГП является блок управления, объединяющий в себе весь операционный и диспетчерский функционал.

Блоки чтения, интерфейса, адаптации, хранения, преобразования данных и визуализации играют служебные роли отдельных, в значительной степени обособленных, операционных элементов. Блок возможной непосредственной интеграции с системами PTC Creo или 3ds Max также обособляется от прочих блоков для осуществления большей гибкости и мобильности коррекции результирующего программного решения.

Блок управления исполняет роль аккумулятора и диспетчера всех операций программного решения. Блоки чтения, сохранения и адаптации данных вынесены в отдельные динамически подгружаемые библиотеки, как и другие блоки

(хранения и визуализации), кроме блока взаимодействия с пользователем — блока интерфейса.

Визуализация САГП может производиться как в одном, так и в нескольких окнах (рис. 2).

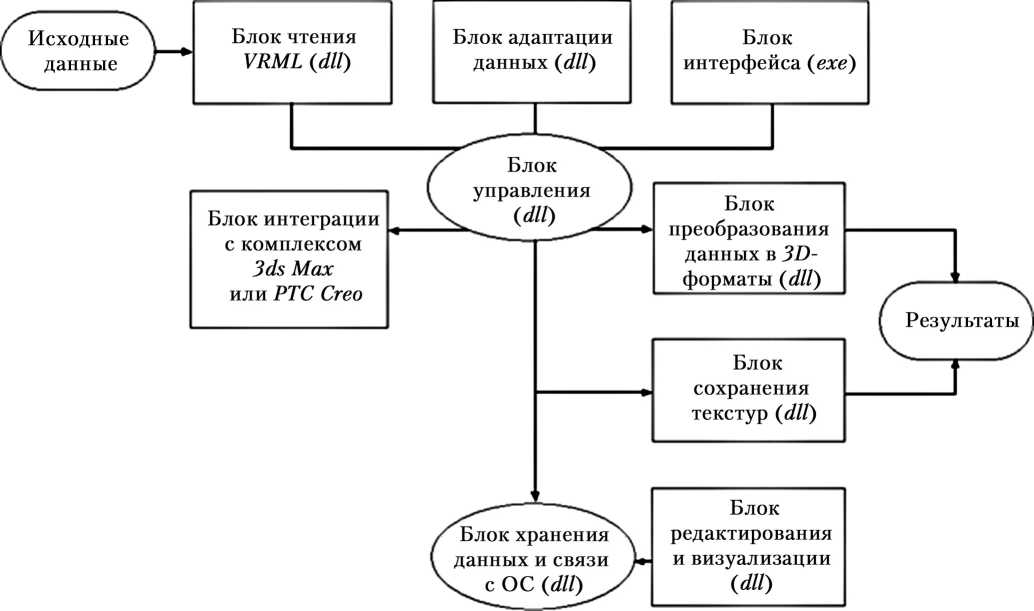
Рис. 1. Схема эскиза архитектуры проекта программного комплекса системы адаптации графического пакета

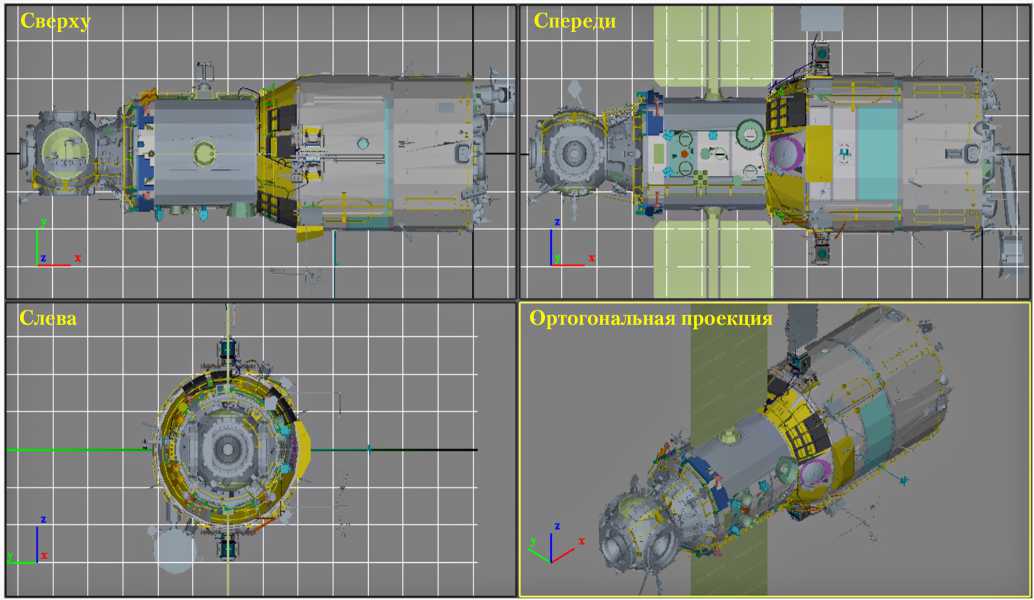
Рис. 2. Рабочая область блока визуализации САГП в режиме отображения: четыре окна, в каждом из окон — один из четырех видов (перспектива и три проекции). Каждое окно подписано именем соответствующего вида

Кроме того, предполагается возможность перемещения, вращения и масштабирования модели аналогично соответствующим действиям в системе 3ds Max [9, 10].

Каждое из четырех окон обрамлено рамкой. Цвет рамки у активного окна желтый. Окно становится активным при нажатии внутри него любой из трех кнопок мыши. По умолчанию активно окно «Перспектива».

Блок интеграции САГП с 3ds Max или PTC Creo вынесен в отдельный независимый модуль (см. рис. 1).

работа со структурой объекта

Помимо возможности управления объектами непосредственно на проекциях, в САГП предусмотрена работа со структурным деревом объекта, отображаемым в левой области экрана. Такое дерево позволяет отмечать выделяемые для дальнейшей работы объекты. Работа над объектами включает в себя:

• •    возможность переименования объектов с последующим изменением имени файла, хранящего информацию об этом объекте;

• •    возможность доступа к изменению атрибутов выделенного объекта (цвет, прозрачность и т. п.);

• •    возможность локации объекта для дальнейшей работы или наоборот — блокирования от каких-либо изменений (удаления).

При указании объекта на активном перспективном изображении происходит автоматический поиск выбранного объекта в структуре его описания, и происходит выделение его символьного идентификатора синим цветом.

Существует возможность выбора объекта непосредственно по имени в структуре дерева. При этом объект окрашивается в синий цвет на всех проекциях рабочего поля САГП.

Редактирование названия выбранного объекта в дереве структуры осуществляется стандартным способом Windows –приложений. Один клик левой кнопкой мыши в активированную область названия объекта позволяет перейти к режиму текстового редактирования. При этом изменение имени автоматически передается в файловую структуру VRML [11].

Отображаемые флажки ( CheskBox ) при каждом объекте позволяют управлять активностью выбранного объекта, т. е. его присутствием в дальнейшей работе. Снять активность выделенного ранее объекта можно путем удаления галочки в соответствующем CheckBox .

Далее приводится пример работы с выбранным объектом на предмет подготовки к процессу решения задач симплификации (рис. 3).

Рис. 3. Демонстрация вариантов отображения объекта

Для этого, как правило, снимается активность для многих «мелких» конструкций, которые могут сильно пострадать в процессе упрощения, а оставляют более крупные элементы, содержащие большое количество треугольников в описании. Для демонстрации процесса симплификации показаны основные варианты отображения объекта с целью повышения наглядности.

Cимплификация

В качестве примера работы функций упрощения сетки (симплификация) для выбранного объекта предлагается рассмотреть указанный элемент люка на рис. 4. Для реализации функции симплификации выбран алгоритм удаления ребер [12].

Рис. 4. Выбор элемента для применения функции симплификации

Процесс симплификации запускается в главном меню последовательностью выбора: Редактирование / Симплификация . При этом на экране автоматически появляются два окна, отображающих последовательно объект до преобразования и после (рис. 5). При этом параметром управления задается процент симплификации сетки объекта путем динамического движения курсора вдоль планки, расположенной в правом верхнем углу рабочего окна САГП, или непосредственным вводом числовых значений.

При этом управление курсором позволяет возвращать исходное состояние преобразованному объекту или сохранять полученный результат для дальнейшего применения в системе 3ds Max .

Исходя из опыта исследования различных алгоритмов симплификации [13–15], можно сделать вывод, что для различных сеточных конструкций один алгоритм может отрабатывать лучше, чем другой. Поэтому САГП не должна ограничиваться одним решением, необходимо постоянно развивать этот функциональный блок, дополняя его новыми алгоритмами.

а)

б)

Рис. 5. Результат работы процедуры упрощения сетки для выбранного элемента конструкции: а — исходный объект, б — объект после упрощения сетки

заключение

Разработанное ПО САГП внедрено в процесс эксплуатации Международной космической станции при разработке УТС. В результате внедрения ПО САГП трудозатраты на создание трехмерной модели транспортного космического корабля в автоматизированном режиме снижаются на 60% по сравнению с ранее применявшимся ручным методом.

Разработанное ПО САГП является одним из примеров функциональной интеграции в CAD –технологиях и имеет блочную открытую архитектуру для внедрения в различные постановки задач подготовки геометрических компьютерных данных. САГП может рассматриваться как исходный блок системы сопровождения жизненного цикла цифровой модели КА для разработки программных средств для управления космическими полетами, подготовки космонавтов и наземного персонала космических комплексов.