Развитие аналитического мышления в процессе решения задач, представленных в текстовой форме

В связи с наступлением информационного этапа в эволюции современного общества особенно актуальным становится развитие аналитического мышления при обучении авиационных специалистов. Этот фактор зачастую становится определяющим для военных специалистов в адаптации к быстро изменяющимся условиям жизни и профессиональным требованиям [1]. Именно поэтому одной из заявленных задач современного высшего профессионального образования является развитие аналитического мышления, что формулируется доктриной «учить думать, а не зубрить».

Рассмотрим перечень профессиональных компетенций, соответствующих дисциплине «Математика», для специальностей 25.05.04 «Летная эксплуатация и применение авиационных комплексов» и 25.05.05 «Эксплуатация воздушных судов и организация воздушного движения» [2].

Профессиональные компетенции для специальности 25.05.04 «Летная эксплуатация и применение авиационных комплексов»:

– ПК-1 — способность самостоятельно приобретать новые знания и умения и использовать их в сфере профессиональной деятельности в части математики;

– ПК-29 — способность обрабатывать результаты исследований и формулировать выводы в части математики;

– ПК-30 — способность использовать математические модели, позволяющие прогнозировать свойства объектов и процессы профессиональной деятельности в части математики.

Профессиональные компетенции для специальности 25.05.05 «Эксплуатация воздушных судов и организация воздушного движения»:

– ОК-1 — способность представлять современную картину мира на основе целостной системы естественно-научных и математических знаний, ориентироваться в ценностях бытия, жизни, культуры в части математики;

– ОК-3 — способность к осуществлению просветительной и воспитательной деятельности в сфере публичной и частной жизни, владе- ние методами пропаганды научных достижений в части математики;

– ОК-5 — умение анализировать логику рассуждений и высказываний, выявлять значение, смысловое содержание в услышанном, увиденном или прочитанном в части математики;

– ОК-7 — свободное владение литературной и деловой письменной и устной речью на русском языке, навыками ведения спора, дискуссии и полемики, публичной и научной речи в части математики;

– ОК-32 — обладание математической и естественно-научной культурой как частью профессиональной и общечеловеческой культуры в части математики;

– ОК-34 — способность приводить доказательства утверждений как составляющей когнитивной и коммуникативной функции в части математики;

– ОК-40 — способность и готовность использовать на практике базовые знания и методы математических и естественных наук в части математики;

– ОК-41 — способность использовать математическую логику для формирования суждений по соответствующим профессиональным, социальным, научным и этическим проблемам в части математики;

– ОК-42 — владение методами анализа и синтеза изучаемых явлений и процессов в части математики;

– ОК-48 — способность совершенствовать и развивать свой интеллектуальный и общекультурный уровень в части математики;

– ОК-49 — способность к самостоятельному обучению новым методам исследования, к изменению научного и научно-производственного профиля своей профессиональной деятельности в части математики;

– ОК-50 — готовность использовать на практике умения и навыки в организации исследовательских и проектных работ, в управлении коллективом в части математики;

– ПК-21 — способность и готовность использовать основные законы естественных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования при решении профессиональных задач в части математики;

– ПК-23 — способность использовать математические, аналитические и численные методы решения профессиональных задач с использованием готовых программных средств в части математики;

– ПК-25 — умение использовать основные приемы обработки экспериментальных данных при решении профессиональных задач в части математики;

– ПК-52 — способность и готовность организовывать самостоятельную и коллективную научно-исследовательскую работу в части математики;

– ПК-133 — способность и готовность внедрять эффективные инженерные решения в практику в части математики;

– ПК-151 — готовность осуществлять анализ, синтез и оптимизацию процессов обеспечения качества испытаний, сертификации продукции с применением проблемно ориентированных методов в части математики;

– ПК-157 — способность осуществлять математическое моделирование процессов и объектов на базе стандартных пакетов прикладных программ в части математики;

– ПК-159 — способность к анализу и синтезу пространственных форм на основе графических моделей, реализуемых в виде чертежей и изображений в части математики;

– ПК-161 — способность использовать математические методы при обработке, анализе и синтезе результатов научных исследований в части математики;

– ПК-162 — способность производить расчет на прочность деталей конструкций при статических и динамических нагрузках при решении профессиональных задач в части математики;

– ПК-173 — способность осуществлять расчет и проектирование в соответствии с техническим заданием с использованием стандартных средств автоматизации проектирования в части математики;

– ПК-174 — способность разрабатывать проектную и рабочую техническую документацию, умение оформлять законченные проектноконструкторские работы в части математики.

Беглого взгляда достаточно, чтобы понять тесную связь этих компетенций с анализом и, соответственно, с аналитическим мышлением.

С точки зрения общей психологии [3] мышление есть наиболее обобщенная и опосредованная форма психического отражения, устанавливающая связи и отношения между познавательными объектами. Задача мышления состоит в раскрытии отношений между предметами, а также в выявлении и отделении их от случайных совпадений. Человек использует различные типы мышления: логическое, творческое, аналитическое, дедуктивное и индуктивное. Наиболее взаимосвязанными из вышеперечисленных видов мышления являются логическое и аналитическое. Задача логического мышления, как правило, состоит в обобщении происходящего, а также в нахождении последовательности и причинно-следственных связей между объектами [4]. Аналитическое же мышление, в отличие от интуитивного, обычно характеризуется умением быстро и эффективно находить наиболее оптимальное решение различных задач [3].

Мы полагаем, что одним из наиболее эффективных способов развития аналитического мышления в математике является решение задач, представленных в текстовой форме. Умение решать задачи является знаковым показателем, отражающим глубину усвоения учебного материала. В процессе решения совершенствуются логические умения проводить анализ и синтез, обобщать и конкретизировать, раскрывать основное, выделять главное в тек- сте и отбрасывать несущественное. Не секрет, что математика проникает почти во все области деятельности человека, поэтому темы задач могут быть весьма разнообразными. Это делает их универсальным средством усвоения понятий и методов изучения различных прикладных дисциплин, освоения умений и навыков практического применения математики, а также обеспечивает формирование межпредметных связей. Межпредметные связи — важнейший фактор современного образования. Качественное усвоение содержания образования предусматривает установление межпредметных и межтематических связей, использование научной терминологии, систематизацию информации, что также предполагает опору на аналитическое мышление [5].

В соответствии с ФГОС 3+, как и со всеми предыдущими образовательными стандартами, математика обеспечивает изучение дисциплин, приведенных в таблице 1.

Таблица 1

	Специальность 25.05.04 «Летная эксплуатация и применение авиационных комплексов»	Специальность 25.05.05 «Эксплуатация воздушных судов и организация воздушного движения»
.в я Я ч к Я я U S ^ 2 я ко У ^>	Информатика	Информатика
	Физика	Теория транспортных систем
	Математическое моделирование и численные методы	Физика
	Механика	Математическое моделирование и численные методы
	Электротехника, электроника	Механика
	Аэродинамика и динамика полета	Материаловедение и теория конструкционных материалов
	Аэронавигация	Электротехника и электроника
	Аэронавигация дальней авиации	Аэродинамика и динамика полета
	Общая тактика и тактика подразделений дальней авиации	Воздушная навигация
	Авиационная картография, топография и геодезия	Тактика
	Автоматизированные системы управления	Военная топография
	Боевое применение управляемых авиационных средств поражения	Летно-технические характеристики воздушных судов
	Боевое применение неуправляемых авиационных средств поражения	Авиационная метеорология
	Применение авиационных комплексов	Проектирование воздушного пространства
	Теория авиационных двигателей	Теория управления воздушным движением
	Конструкция воздушных судов	Автоматизированные системы управления

Окончание таблицы 1

	Специальность 25.05.04 «Летная эксплуатация и применение авиационных комплексов»	Специальность 25.05.05 «Эксплуатация воздушных судов и организация воздушного движения»
я Я ч к Я я U Я 2 я ю а.» Я ^	Наземные радиосветотехнические средства обеспечения полетов	Метрология, стандартизация и сертификация
	Авиационные радиоэлектронные системы	Теория и методика наведения
	Авиационные приборы и навигационнопилотажные комплексы	Проектирование воздушного пространства
	Авиационная метеорология	Безопасность жизнедеятельности
	Безопасность жизнедеятельности	Боевое применение неуправляемых авиационных средств поражения
	Метрология, сертификация и стандартизация	Боевое применение управляемых авиационных средств поражения
	Теория конструкционных материалов	Авиационные радиоэлектронные системы
	Материаловедение	Управление качеством

Перечень дисциплин, изучение которых обеспечивает математика

С помощью задач, представленных в текстовой форме, можно построить межпредметные связи практически с любой из перечисленных дисциплин. Решение специализированных задач не только будет способствовать развитию аналитического мышления, но и повысит интерес курсантов к изучаемым предметам [6].

Можно выделить следующие этапы решения текстовых задач [7].

I этап. Восприятие и осмысление текста задачи.

Целями данного этапа являются: понимание ситуации, описанной в задаче, в целом, выделение условий и требований, обозначение извест- ных и искомых объектов, а также выделение всех зависимостей между обозначенными объектами.

II этап. Поиск плана решения.

На данном этапе учащимся необходимо установить связь между данными и искомыми объектами, наметить последовательность действий по решению задачи.

• III    этап. Составление плана решения задачи.

Цель: записать последовательность действий по решению задачи.

• IV    этап. Осуществление плана решения.

Цель: найти ответ на вопрос задачи в соответствии с выбранным планом решения.

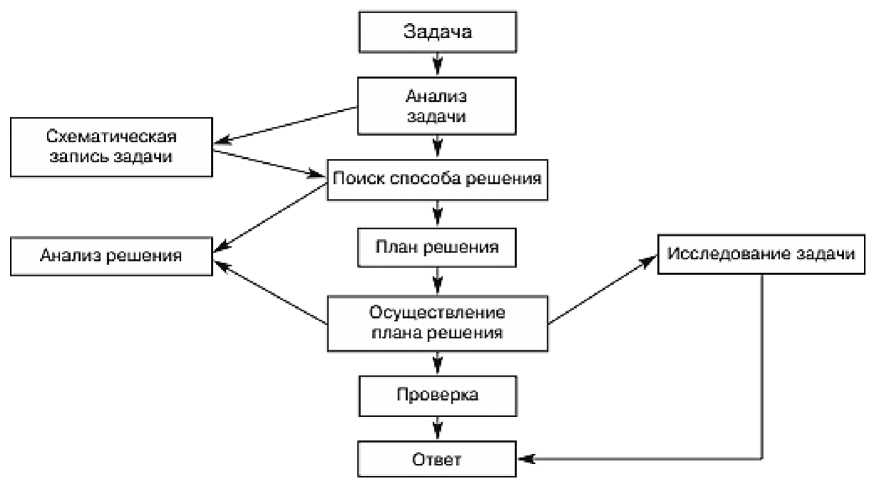
Рис. 1. Алгоритм решения задачи, представленной в текстовой форме

• V    этап. Проверка правильности решения.

Цель: установить правильность или ошибочность выполненного решения.

Все этапы можно преобразовать в схему, представленную на рисунке 1.

Использование теории вероятностей в военном деле было связано с решением задач по повышению эффективности применения боевой техники и средств поражения, улучшению качества ведения боя [4]. Представим задачу, связывающую теорию вероятностей с военной дисциплиной «Общая тактика».

Пример. Имеется по три ракеты двух типов. По одной и той же цели намечен пуск ракет сначала первого типа, затем — второго. При первом же попадании цель разрушится и пуск ракет прекратится. Вероятность попадания при пуске одной ракеты первого типа Р₁ = 0,1 , для ракет второго типа — Р₂ = 0,2 . Найти вероятность того, что цель разрушена после четвертого пуска.

Решение. Применим наш алгоритм на примере решения данной задачи.

I этап. Восприятие и осмысление текста.

Итак, по условию задачи есть пять ракет. Сначала используют три ракеты первого типа. Поскольку попадание наступило с четвертого раза, значит, первые три ракеты по цели не попали. Далее запускают ракеты второго типа. И тогда при первом же запуске ракеты второго типа (это четвертый пуск) происходит попадание, так как по условию задачи попадание произошло с четвертого раза.

II этап. Поиск плана решения.

Итак, нам нужно знать вероятность промаха ракетами первого типа. Далее, поскольку произведено четыре выстрела, а значит, четыре элементарных исхода, нам нужны вероятности для каждого из них. Затем, поскольку все эти события происходят одно за другим, мы имеем дело