Развитие интеграции (синтеза) технологий и методов при изучении математических дисциплин студентами естественнонаучных специальностей

Реформирование российского высшего профессионального образования предусматривает, в первую очередь, интеграцию на разных уровнях: формирование единого европейского пространства высшего образования (ЕЕПВО); современную интеграцию образования и науки; межпредметную и внутрипред-метную интеграцию при обучении студентов вузов и др.

«Образование, наука и культура все более превращаются в сферу международной конкуренции и, вместе с тем, сотрудничества. В современных условиях успешную карьеру может обеспечить только такая система образования, которая учитывает процессы глобализации: выпускникам вузов придется жить и работать в новом мире, в котором границы национальных экономик и культур делаются все более условными» [1].

Следствием глобализации экономики стала глобализация образования. Востребованность высококвалифицированных специалистов опережает темпы роста их подготовки. В образовательной политике стран Западной Европы установились тенденции к улучшению образовательных достижений, исследовательско-инновационной работы.

Очевидно, что «современное общество столкнулось с рядом серьезных кризисных процессов глобализационного, социально- го и экологического характера. Как самостоятельные сферы социальной жизнедеятельности образование и наука становятся все менее самодостаточными и дееспособными. Данные социальные системы должны составлять неразрывный синтез, предполагающий последовательную реализацию комплекса интеграционных проектов и программ» [3].

Учебный процесс должен быть связан с научно-исследовательской работой, только тогда появятся научные достижения, инновационные проекты. Для современной науки характерны комплексные методы познания.

Интегративный подход определяет условия построения образовательной системы и осуществления образовательного процесса. Основными формами реализации принципа интеграции в образовательном процессе являются внутрипредметная интеграция и межпредметная.

В настоящее время нет необходимости доказывать важность межпредметных связей в процессе обучения. Они способствуют формированию понятий внутри отдельных предметов и систем, так называемых межпредметных понятий, т. е. таких, полное представление о которых невозможно дать студентам на занятиях по какой-либо одной дисциплине (понятия о различных процессах).

Осуществление межпредметных связей помогает формированию у студентов цельного представления о явлениях в мире и взаимосвязи между ними, позволяет усвоить знания и умения, использовать их при изучении других предметов, применять в будущей профессиональной деятельности.

Целесообразным признается использование таких уровней интеграции:

• 1)    тематическая (междисциплинарная) -одна тема раскрывается на основе двух-трех учебных предметов (иллюстративноописательный уровень);

• 2)    проблемно ориентированная – одна проблема решается методами разных наук;

• 3)    концептуальная (концепция раскрывается на основе различных предметов, используется совокупность средств и методов);

• 4)    теоретическая (философское взаимопроникновение различных теорий).

Внутрипредметная и межпредметная интеграция предполагает три основные стадии:

• 1)    освоение знаний и приобретение навыков путем повтора упражнений;

• 2)    формирование умений для использования знаний в других ситуациях;

• 3)    смыслообразование.

Две первые стадии реализуются в процессе образования. Третья стадия – смыслообра-зование – происходит в процессе перестройки дидактической системы. Механизмом междисциплинарной интеграции являются межпредметные связи. В интегрированном учебном плане дисциплины пересекаются, взаимодействуют их компоненты. По мере усвоения студентами предметного материала нарастает внутрипредметная интеграция. Основным механизмом и средством интеграции при этом выступают внутрипредметные связи.

Взаимосвязь со смежными дисциплинами увеличивает количество опорных знаний, обязательных для понимания учебного материала по предмету. Интеграция с предметами и темами, привлекательными для студентов, повышает интерес к дисциплине и развивает мотивацию к ее изучению.

Интеграция в обучении предполагает интеграцию методов, содержания и форм. В связи с высоким уровнем интеграционных процессов в высшем образовании предполагается активное участие студентов и преподавателей в этих процессах. Причем в условиях личностно ориентированной парадигмы студент становится в центре образовательного процесса, им формируется интегрированная личностно ориентированная образовательная среда. Традиционное аудиторное обучение, способствующее формированию математического мышления, не индивидуализировано, ориентировано на стандартные задачи, что приводит к его недостаточной эффективности.

Таким образом, в модернизации высшего образования одной из основных идей считается междисциплинарная (взаимосвязи содержания ряда учебных дисциплин) и внутри-предметная (синтез и взаимосвязь при обучении реализуются на уровнях специфического материала по дисциплине) интеграция. Реализация внутрипредметных и межпредметных связей при обучении студентов вузов способствует приобщению их к опыту учебнотворческой математической деятельности. При этом в поиске метода и способа решения задачи формируются интегративные умения. Развитие креативности, приобщение студентов к профессионально-творческой деятельности осуществляются через использование специальных задач по высшей математике, математическому моделированию на основе интегративно-компетентностного подхода.

Комплексы таких специальных задач предлагаются автором для формирования многомерной профессионально-творческой компетентности студентов вузов естественнонаучных специальностей. Интеграцию средств, методов, содержания и форм рекомендуем осуществлять посредством специальных математических задач [5–6]. Например, при изучении раздела «Аналитическая геометрия» рекомендуем студентам следующую задачу.

Задача. Даны координаты вершин пирамиды: А₁ (2; 3; 4), А₂ (4; 0; –2), А₃ (5; 1; 4), А₄ (2; 3; –4). Найти объем пирамиды всевозможными методами и способами.

Объем пирамиды найдем двумя способами.

1-й способ (векторный). Объем пирамиды А₁А₂А₃А₄ найдем, используя формулу для нахождения объема треугольной пирамиды:

V = 1/6 | → a, → b,

→ → на на векторах a, b,

^→ c | пирамида построе-

→ c, ).

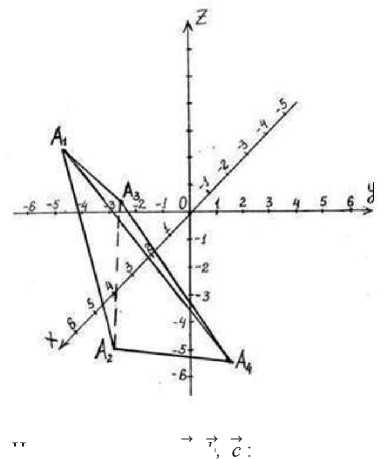
Находим векторы a, b,

a ^→ = A₁A₂ (2; 3; –6), ^→ b = А₁А₃ (3; 4; 0),

→ c

→ ( a,

= А1A4 (0; 6; –8).

→ → b, c ) =

–6

3 4 0 = 2∙4∙(–8) + 3∙0∙0 +

–8

+ 3∙6∙(–6) – 4∙0∙(–6) – 3∙3∙(–8) – 6∙0∙2 = – 64 – – 108 +72 = – 100;

– 3 ∙ 3 ∙ (–8) – 6 ∙ 0 ∙ 2 = –64 – 108 +72 = –100;

V A ₁ A ₂ A ₃ A ₄= 1/6 │–100│ = 100/6 = 50/3 = 16 ²/ 3 .

Ответ: объем пирамиды равен 16 ²/ 3 .

2-й способ (векторно-аналитический) . Найдем уравнение плоскости, проходящей через точки А₂, А₃, А₄:

x – 4 y – 0 z + 2

5 – 4 1 – 0 4 + 2

2 – 4 3 – 0 –4 + 2

x – 4 y z + 2

1      16

–2   3–2

= 0.

=0.

–2 ∙ (x – 4) – 2 ∙ y ∙ 6 + 3 ∙ (z + 2) + 2 ∙ 1 ∙ (z + + 2) + 2y – 3 ∙ 6 (x – 4) = 0

–20x – 10y + 5z + 90 = 0;

–4х – 2y + z +18 = 0.(1)

Уравнение (1) является уравнением плоскости, проходящей через точки А2, А3, А4. Найдем расстояние от точки А1 до этой плоскости, т.е. высоту пирамиды:

h = │–4х – 2y + z +18│/ (4, 5826) = │–8 + 6 + +4 +18│/(4, 5826) ≈ 20 / (4, 5826) ≈ 4,364.

A2A3 = 38 ≈ 6,164; A3A4 = 77 ≈ 8,775;

A2A4 = 17 ≈ 4,123. (9,531 – 8,775)

Площадь основания пирамиды найдем по формуле Герона:

p/2 ≈ (6,164 + 4,123 + 8,775)/2 ≈ 9,531.

S =V 9,531 · (9,531 – 6,164) · (9,531 – 4,123) · (9,531 – 8,775) ≈ to V 131,199 ≈ 11,4542.

V A ₁ A ₂ A ₃ A ₄ = ¹/ 3 ∙S ∙ h ≈ ¹/ 3 ∙ 11,4542 ∙ 4,364 ≈ 3,8181 ∙ 4,364 ≈ 16,66 ≈ 16 ²/ 3 .

Ответ: объем пирамиды равен 16 ²/ 3 .

Существует еще несколько способов решения данной задачи.

3-й способ. Найдя длины сторон основания пирамиды и угол между двумя сторонами основания треугольника как косинус угла между двумя составленными векторами и по формуле: половина произведения сторон на синус угла между ними, найдем площадь основания пирамиды; далее решаем как в первом или втором способе.

4-й способ . Найдем угол между двумя сторонами основания по теореме косинусов и опять же по формуле: половина произведения сторон на синус угла между ними: найдем площадь основания пирамиды; далее решаем как в первом или втором способе;

5-й способ. Также площадь основания пирамиды можно найти, составив уравнение одной из сторон треугольника и найдя длину высоты в этом треугольнике как расстояние от точки (третьей вершины основания) до пря- мой; далее решаем как в первом или втором способе.

Студенты могут найти эти решения самостоятельно.

Получается, что при решении данной задачи задействовано много тем из геометрии, поскольку эту задачу можно решить многими способами. Не ограничиваясь одним способом решения, мы задействовали много вну-трипредметных связей. Кроме того, мы использовали связи дисциплин внутри математического цикла: высшей математики, аналитической геометрии, линейной алгебры; также задействовали несколько тем: определители матриц, нахождение площадей треугольника разными способами, нахождение объемов в пространстве, уравнение плоскости в пространстве, расстояние от точки до плоскости, операции с векторами и т.д. Также операции с матрицами, векторами, площадями, объемами, расстояниями в пространстве используются и в межпредметных связях: в физике, химии, начертательной геометрии и других дисциплинах.

«На наш взгляд, эффективность образовательных процессов в первую очередь зависит от осознания их участниками и организаторами сущности и роли интегративного характера связей внутри системы, целенаправленного их стимулирования и развития. Значит, в процессе профессиональной подготовки студентам необходимо показывать, каким образом осуществляется интеграция элементов, на каком этапе и как происходит потеря несущественных свойств объединяющихся элементов, почему важно сохранить автономность интегрируемых элементов, как возникают новые свойства систем с интегративным качеством» [2].

Одновременно следует рассматривать процессы дифференциации, которые показывают технологии разложения и целостного функционирования, т. к. интеграция и дифференциация взаимосвязаны.

В современной действительности усиливается математизация курсов разных дисциплин. Высшая математика дает будущим специалистам систему знаний и умений, необходимых в профессиональной деятельности, а также для изучения смежных дисциплин (физики, технологии, химии, черчения и др.). На основе знаний по математике у студентов формируются общепредметные знания. При этом при практическом применении получаемых студентами знаний и умений у них формируются научное мировоззрение, представления о математическом моделировании как о методе познания действительности.

Кроме занятий со специальными задачами, преподавателям рекомендуется применять проектное обучение. Тема проекта должна содержать межпредметные и внутрипред-метные связи. Целями проектных занятий являются обеспечение внутрипредметной и межпредметной интеграции, индивидуализация учебных занятий, что способствует развитию профессионально-творческих компетентностей, самостоятельности.

Лучшие результаты могут быть презентованы на конференциях, работа над проектами продолжается студентами зачастую и после окончания курса. У студентов появляется интерес к науке.

После применения рекомендованных автором комплексов задач на развитие интеграции в учебном процессе [4–5] проведено сравнение результатов формирования многомерных профессионально-творческих компетентностей студентов вуза в экспериментальной и контрольной группах. Успеваемость по математическим дисциплинам повысилась, и формирование многомерной профессиональнотворческой компетентности в результате применения данных комплексов задач улучшилось в среднем на 12-14% (о критериях оценок -в других работах). Результативность применения рекомендованных автором комплексов задач обеспечивается и содержанием учебного материала, и их эффективностью и личностным интересом студентов к задачам данного комплекса, возможностью индивидуальной и групповой работы, балльно-рейтинговой оценкой деятельности.