Развитие представлений о деформационно-прочностных свойствах мякоти картофельных клубней

Механическая переработка растительного сырья происходит с большими затратами энергии. В полной мере это относится к переработке картофеля, существенная часть урожаев которого идет на истирание для последующего получения крахмала [1]. Поэтому параметры деформационно-механических характеристик картофеля должны входить в расчетные формулы разрабатываемых технологических машин и аппаратов и рациональных процессов,

определяющих их работу. Вместе с тем отсутствуют устоявшиеся представления о функциональной связи между деформационными и прочностными характеристиками картофельных клубней, количественном влиянии на изменения деформационных свойств в процессе хранения картофеля, формализации этого влияния в виде количественного параметра, который мог бы входить в расчетные формулы.

Важные и объективные результаты по механическим характеристикам получают в испытаниях при одноосном сжатии цилиндрических образцов, что в РФ и за рубежом является обязательным для конструкционных материалов [2]. Такие же исследования выполнялись и для растительных материалов, включая картофель [3,4]. Современные испытания обычно проводят в машинах с автоматическим непрерывным нагружением и, как правило, со свежими, жесткими клубнями. В результате получают диаграммы, малочувствительные к побочным, но важным для механической переработки картофеля эффектам. К ним относятся релаксация напряжений в процессе испытаний [5], смена характера деформаций по мере их роста, отражающаяся в S-образном виде диаграмм [6], и другие особенности, обусловленные влиянием вялости клубней, усиливающейся в процессе хранения [7]. Вследствие новизны работ в них дается фрагментарная и разобщенная трактовка обнаруживаемых эффектов.

Цель работы – обобщение выявленных новых особенностей и развитие представлений о деформационно-прочностных свойствах мякоти картофельных клубней, различающейся по степени жесткости.

Материалы и методы

Исследования деформационно-прочностных свойств проводили в условиях одноосного сжатия цилиндрических образцов картофеля, имевших начальную длину l 0 и площадь круглого поперечного сечения А 0 . При этом фиксировали изменение их длины l в виде укорочения (абсолютная деформация) ∆ l = l – l 0 (мм) в зависимости от усилия сжатия F (Н). Полученные экспериментальные величины пересчитывали в напряжение сжатия образца в виде осевой силы, отнесенной к его начальной площади σ = F / А 0 (МПа), и соответствующую ему относительную деформацию ε (в дальнейшем – деформация) в виде отношения величины абсолютной деформации к начальной длине образца ε = ∆ l / l 0 (б/р).

Лабораторная установка позволяла определять усилие сжатия F образца по величине прогиба свободного конца консольно-закрепленной упругой пластины. Изменение нагрузки обеспечивали через механическую винтовую передачу механическим поворотом маховика, позволяющую делать промежуточные остановки в нагружении и полные промежуточные разгрузки со следующими за ними догружениями. Усилие сжатия постепенно увеличивали с периодическими 30-секундными перерывами на время основной релаксации напряжений в образце. Величину усилия сжатия F образца определяли по тарировочному графику без учета той части общего усилия, которое требовалось на прогиб пластины. Величину прогиба упругого элемента фиксировали с помощью индикатора часового типа. Деформацию образца измеряли по изменению расстояния между сжимающими его подвижными основаниями.

Испытанию подвергали цилиндрические образцы диаметром d 0 = 14 мм. Величина диаметра обеспечивала возможность разрушения образца на лабораторной установке. Высоту l 0 образца экспериментально подбирали наибольшей при условии обеспечения нагружения без его перекосов и изгиба, т. е. без потери устойчивости. Она составила 25 мм.

Результаты и обсуждение

С самого начала было выявлено падение сжимающего усилия во время остановки нагружения для проведения промежуточных замеров величин усилия и деформации. Это показало наличие релаксационного эффекта, свойственного мякоти образцов картофельных клубней при ее деформации, что заставляет исследователей указывать в аналогичных испытаниях скорость непрерывного нагружения в автоматическом режиме [8]. В этой связи дальнейшие замеры проводились с 30-секундными остановками при последовательном нагружении образцов. Во время остановок скорость падения усилия снижалась от интенсивной до малосущественной. При 30-секундной остановке величина падения усилия составляла 4–12% [5]. Также была отмечена особенность формы диаграмм в начале нагружения. От нуля и до напряжения, близкого к σ ≈ 0,1 МПа, происходит существенный рост деформации образца при незначительном росте нагрузки, т. е. образец проявляет высокую податливость (рисунок 1).

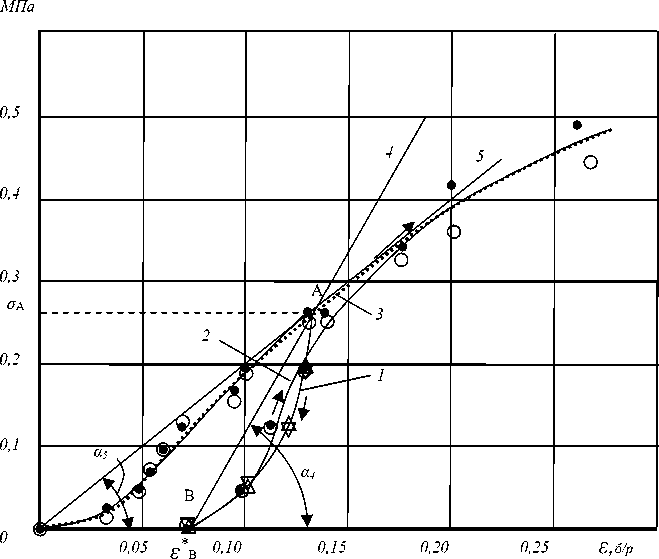
Рисунок 1. Характерная диаграмма сжатия образца клубня с однократным промежуточным разгружением и последующим догружением: точки – стадия нагружения; окружности – после релаксации в стадии нагружения; треугольники вершиной вниз – стадия разгружения; треугольники вершиной вверх – стадия догружения; 1 и 2 – промежуточная разгрузка и повторное нагружение соответственно; 3 – пунктирная S-образная диаграмма без учета промежуточной разгрузки; 4 – прямая, соответствующая промежуточной разгрузке ВА; 5 – прямая ОА, соответствующая начальной деформации образца; σ А – напряжение, с которого началась промежуточная разгрузка; ε B – остаточная деформация после промежуточной разгрузки; α 4 – угол наклона прямой 4; α 5 – угол наклона прямой 5 Figure 1. Characteristic diagram of the compression sample of the tuber with a single unloading and subsequent re-loading: points – the stage of loading; circles – after relaxation, under loading; the triangles top down – stage of unloading; the triangles top-up – re-loading stage; 1 and 2 – intermediate unloading and re-loading, respectively; 3 – dotted S-shaped figure without taking into account intermediate unloading; 4 – straightened line corresponding to the intermediate unloading VA; 5 – straightened line OA corresponding to the initial deformation of the sample; σ А tension, which began with intermediate unloading; ε B is the residual deformation after intermediate unloading; α 4 – the angle of slope of the straight 4; α 5 is the slope of the straight 5

При этом к моменту достижения напряжений σ ≈ 0,1 МПа отмечается явное увеличение деформации образцов с увеличением степени вялости их мякоти [6]. При дальнейшем увеличении напряжения ( σ > 0,1 МПа) угол наклона диаграммы к оси абсцисс, характеризующий жесткость образцов, существенно возрастал. Таким образом, напряжение σ ≈ 0,1 МПа оказалось характерным для образцов из клубней различающейся вялости, и потому оно принято в качестве рубежного.

Криволинейность полной диаграммы, казавшаяся в начальных экспериментах со свежим картофелем незначительной и не всегда отчетливо проявлявшаяся при σ > 0,1 МПа, оказалась весьма важной для понимания характера деформаций в процессе нагружения образцов. Дальнейшие эксперименты показали, что ее вид, близкий к прямолинейному, даже включая начальный участок нагружения, свойственен для жестких (свежих) картофельных клубней. Для вялых клубней форма диаграммы отчетливо становилась S-образной [6], и ее кривизна увеличивалась с усилением вялости клубней.

Особенностью деформационных свойств образцов оказалось сочетание больших деформаций к моменту разрушения, близких к 0,3, и само разрушение по плоскости, наклоненной под углом 45° к оси образца. Такие большие деформации характерны для пластичных материалов, а такое разрушение указывает на разрушение по плоскости действия наибольших касательных напряжений, т. е. как хрупкое. К хрупким конструкционным материалам условно относят те, которые имеют малые остаточные деформации до 6%. Эта парадоксальность объясняется клеточным строением растительных материалов, имеющих большое количество внутриклеточной жидкости [6]. Вслед за зоной упругой деформации, завершающейся в области значений напряжений σ ≈ 0,1 МПа, начинается разрушение отдельных клеток, которое постепенно перерастает в преимущественное слияние смежных разрушенных клеток, что приводит к интенсивному росту деформаций. Происходит постепенное разрушение первоначальной структуры материала, что нехарактерно для пластичных материалов, сохраняющих свою структуру до полного разрушения образца. А хрупкий вид разрушения свидетельствует о том, что целостность формы образцов с конечной малосущественной бочко-образностью сохраняется оставшимися пока неразрушенными клетками вплоть до разрыва, т. е. как у хрупкого материала.

Анализ диаграмм указывает на то, что клеточная структура материала образца, вырезанного из клубня картофеля, разрушается, сохраняя подобно пластичному материалу большую остаточную деформацию, близкую к значению 0,3, но является хрупкой, поскольку разрушение происходит по плоскости, наклоненной под углом 45° к продольной оси образца. В этой связи диаграмма показывает гибридный деформационнопрочностной тип разрушения клеточной структуры мякоти клубня.

S-образную диаграмму исследователи получали и ранее [9]. Однако в обсуждениях формально ее не отмечали и не увязывали с особенностями происходящих внутренних процессов на уровне клеточного строения мякоти. То же относится к известному факту появления значительных остаточных, т. е. неупругих, деформаций при снятии нагрузки задолго до разрушения образца. Однако оба этих фактора влияют на возможность использования формулы Гука в традиционном виде входящих в нее обозначений в качестве расчетной формулы для растительных, т. е. имеющих клеточную структуру, материалов:

σ = Еε , (1)

где Е – коэффициент, имеющий название модуля продольной упругости, или модуля Юнга.

Так, в публикациях по исследованию механических свойств растительных материалов коэффициент, обозначаемый в формуле Гука (1) буквой Е, определяют по тангенсу угла наклона прямолинейной или условно спрямленной (идеализированной) диаграммы, соединяющей начало координат с точкой разрушения образца, и называют модулем Юнга [4, 10, 11]. При этом не учитывается существование в зонах его определения неупругих деформаций, хотя по своему физическому назначению он должен отражать поведение материала только в упругой области. Наличие остаточных деформаций в зонах определения модуля для растительных материалов не вызывало вопросов к обоснованности использования термина «модуль Юнга».

Остаточные деформации выявлялись, начиная с напряжения σ ≈ 0,1 МПа. Для фиксации неупругих деформаций в процессе нагружения образцов эксперименты выполнялись в зоне σ > 0,1 МПа с промежуточными разгрузками и следующими сразу за ними повторными догружениями [6]. В течение нагружения производились от одной до трех таких промежуточных разгрузок и догрузок. После каждой разгрузки отмечалось наличие существенной остаточной, т. е. неупругой, деформации. На рисунке 1 она обозначена символом ε * B . Значит, модуль, определяемый по тангенсу угла наклона прямолинейной диаграммы или ее идеализированных прямых на участках, где в образце возникают напряжения σ > 0,1 МПа, не может называться модулем Юнга и должен носить иное название, например, деформационно-прочностной модуль, или модуль жесткости, и другое обозначение, например, Z . Тогда формула, аналогичная формуле Гука (1), будет иметь вид:

σ = Zε , (2) где Z – выполняет ту же функцию коэффициента пропорциональности, что и Е .

Кривизна линии промежуточной разгрузки напоминает кривизну диаграммы в начале нагружения. Однако прямая ВА (прямая 4 на рис. 1), относящаяся к периоду промежуточной разгрузки и соответствующая только упругим деформациям, имеет больший угол наклона α4 к оси абсцисс, чем прямая ОА, относящаяся к начальному этапу нагружения и наклоненная под углом α 5 (прямая 5 на рис. 1). Значит, в начальный период нагружения к упругой деформации добавляется неупругая, увеличивая общую деформацию и уменьшая α 5 . Это наблюдение практически подтверждает введенный как гипотеза в работе [8] аналогичный вывод.

Для образцов, вырезанных из мякоти клубней различающейся вялости, модуль Z окажется различным. Это требует учета зоны диаграммы, для которой он был получен при его использовании непосредственно в общих формулах расчета оборудования механической переработки картофеля. Нужны дополнительные показатели, учитывающие и степень вялости клубня, и зону, для которой показатель вычисляется по (2).

Кривизна диаграммы промежуточных разгрузок свидетельствует о сложном механизме деформации материала, а практическое совпадение кривых разгрузки и следующего непосредственно за ней нагружения указывает на отсутствие в этих процессах неупругой составляющей деформации. Значит, деформация образца в промежуточных разгрузках является упругой, хотя ее диаграмма имеет криволинейный вид, аналогичный начальной и примыкающей к ней зоне диаграммы нагружения. Это подтверждает наличие и рост упругих деформаций даже в зонах начального появления и роста неупругой деформации. Промежуточные разгрузки показали наличие остаточных деформаций в образце, что обязывает ввести в линейную зависимость Гука модуль жесткости Z вместо модуля Юнга, используемого для характеристики только упругих свойств материалов.

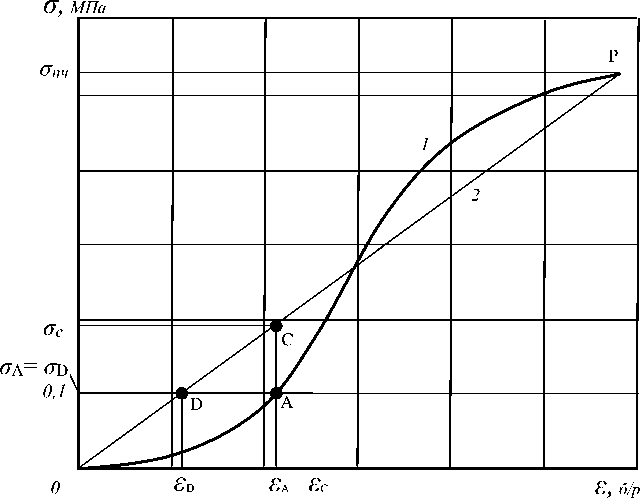
Рисунок 2. Диаграммы образцов: линия 1 – S-образная диаграмма исследуемого вялого клубня; линия 2 – прямолинейная идеализированная диаграмма, характерная для жесткого клубня; ε А – деформация образца из вялого клубня; σ С и ε С , ε D – напряжение и деформации по идеализированной диаграмме образца, соответствующего жесткому клубню; σ А = σ D = 0,1 МПа – напряжение в вялом и идеализированном жестком образцах соответственно; σ пч – предел прочности материала образца; Р – точка разрушения образца

Figure 2. Chart samples: line 1 – S shaped graph of the studied sluggish tuber; line 2 idealized straight-line diagram, typical for a hard tuber; ε А – deformation of a sample from a sluggish tuber; σ С and ε С , ε D – stress and deformation in the idealized diagram of the sample corresponding to the hard tuber; σ А = σ D = 0.1 MPa, the stress in idealized sluggish and hard samples, respectively; σ пч – tensile strength of the sample material; P – the point of destruction of the sample

Выявление в S-образном виде диаграммы зон, отражающих при нагружении характерные особенности постепенных разрушений в образце, позволило сформировать критерии оценки степени жесткости клубней (рисунок 2) [7]. Они сформированы таким образом, что пределы их изменения лежат в диапазоне от нуля до единицы и вычисляются по экспериментальным табличным данным или значениям, составляющим критерии показателей на диаграмме разрушения. Их назначение состоит в том, что они должны входить в виде сомножителя в формулы расчета оборудования механической переработки, например, терки для истирания картофеля в крахмалопаточном производстве. Они дают возможность учитывать для каждой зоны диаграммы вялость клубней в формулах механического расчета оборудования. Каждый критерий отражает определенную особенность диаграммы и свойств мякоти картофеля и может быть получен в виде числа, предназначенного для включения его в расчетные формулы технологического оборудования и осуществляемых в нем процессов.

Из рассмотренных в [7] трех типов критериев к наиболее универсальным и информативным следует отнести k 1 и k 2 , что объясняется простотой получения данных для их расчета и чувствительностью к изменению вялости клубней.

Критерий k 1 основан на различии деформации образцов в начальной стадии нагружения, когда напряжение в них достигает σ = 0,1 МПа (рисунок 2):

k i = I D (3) ⁶ A

Критерий по (3) представляет собой отношение деформации ε D по идеализированной прямолинейной диаграмме к деформации ε А образца по диаграмме исследуемого вялого клубня.

Критерий k 2 основан на различии напряжений по диаграмме образца из вялого клубня и идеализированного жесткого в тот момент, когда в исследуемом вялом образце напряжение достигает σ В = 0,1 МПа:

k 2 = ^ A . (4)

" .

Критерий представляет собой отношение напряжения σ A = 0,1 МПа в исследуемом образце к напряжению σ C по идеализированной прямолинейной диаграмме при той же деформации. Оба напряжения соответствуют равной деформации ε A = ε С .

Чем меньше соотношения (3) и (4), тем более вялым был исследуемый клубень. Параметры в числителях и знаменателях формул (3) и (4) определяются непосредственно из экспериментально полученных диаграмм (рисунок 2) или по таблицам, как это принято для конструкционных материалов. Эти параметры интенсивно меняются с ростом вялости картофельных клубней и отражают начальный этап деформирования, в значительной мере определяющий эффективность работы любого механического измельчителя. Их универсальность и информативность связаны, например, с тем, что знание величин k 1 или k 2 , выражающих количественно степень жесткости картофеля, позволит заранее назначать величину необходимого перемещения