Развитие у обучающихся навыков решения в аналитическом виде уравнений математической физики с применением Maple

В настоящее время теоретические положения и практические методы математической физики применяют фактически во всех областях человеческой деятельности – охрана окружающей среды, геофизика, гидродинамика, электродинамика, акустика, социология, медицина, теория упругости и др. Кроме того, интенсивное развитие методов и средств математического и компьютерного моделирования позволило сделать процесс решения задач математической физики более эффективным. Поэтому обучение владением методами и инструментарием компьютерного моделирования для решения уравнений в частных производных является крайне важным. Инструментарием компьютерного моделирования служат различные программные системы – MATLAB, Maple и др. [14]. При их помощи можно решать различные задачи [4-8].

Постановка задачи

В данной работе, используя систему Maple [1-3], рассмотрен процесс аналитического решения одномерного неоднородного гиперболического уравнения:

д ² u ( x, t )

₉ д ² u(x,t)       .    .

^{2           +} f ( x • ' )

С начальными условиями (задача Коши):

u (x,0) = y(x); ut (x,0) = ^(x).     (2)

Для большей наглядности решение представляется в графическом виде.

Уравнение (1), например, является математической моделью малых поперечных колебаний струны, представляющей собой не сопротивляющуюся изгибу натянутую нить. Кроме того, это уравнение описывает также малые продольные колебания упругого стержня.

Поиск аналитического решения

Зададим для (1) и (2) конкретные значения:

a = 2; f ( x , t ) = A • sin ( a x + p t ) ³ • e"^ + 10 • x ³ + 2 • x ²;

A = 10; a = 35; в = 95;

u ( x ,0 ) = ф ( x ) = 4 • cos ( 49 • x ) - 5 • sin ( 47 • x ) + 4 • x ³ - 52 • x ² ;

ut (x, 0) = щ (x) = 4 • cos (3 • x) - 8 • x2 + 6 • x.

В этом случае (1) и (2) примут следующий вид:

5 ² u(x , Л     d ² u(x , Л          ,

----v = 4----V + 10 • sin ( 35 x + 95 t ) ³ • e ⁴ t + 10 • x ³ + 2 • x²       (3) 5 t ²             5 x²

u (x, 0) = 4 • cos (49 • x) - 5 • sin (47 • x) + 4 • x3 - 52 • xx ut (x,0) = 4 • cos (3 • x)- 8 • x2 + 6 • x

Исходный текст на Maple для решения (3) с (4) может быть таким:

> restart

> with^ VectorCalculus) :

> with^inttrans) :

> with(PDEtools) :

> declare(u{x, t), v(x, t))

uLx, t) will now be displayed as и v(x, /) will now be displayed asv

> my_f{x, t) — A -sin³(ct-x + P?) -exp( -4V) + 10- x³ + 2-x² :

> a := 2 : A — 10 : a — 35 : p ~ 95 :

> ftOx := 4-cos(49-x) — 5-sin(47x) + 4-x³ — 52-x² :

> ft0x_t — 4-cos(3-x) — 8-x² + 6-x :

d2             7

> my PDF и ••= —yu^x, t) = a¹ ■ Laplacian(u{x, t), [x]) + my f(x, t)

"            dr my PDF и •= и, = 4u +10 sin(35x + 95 f)3 e 4 ? + 10x3 + 2x2

> my_solve_u — pdsolve{my_PDF_u)

,                                        A -V4 X5 , 5700e“4zcos(35x + 95 /)

my_solve_u — u = _Fl{2t +x) + _F2(2t-x) - —--- — H-- 1-7^^1/101-------

24     о             1 /4о14о1

_ 61635e~^4zsin(35x + 95 ?) _ 5700e~^4fcos( 105x + 285/) 34922962                  1382276281

185545 e~4 zsin(l05 x + 285 Г)

> ^-Переход к однородному уравнению

> #v(x, Р = и(х, А — и

> #Выделяем частное решение и г          части

> ичастн-= add{ ор( i,op(nops(my_solve_u),my_solve_u}) , i = 3

..nopsiopi nops^my_solve_uy my_solve_u^ );

,₌ _ x⁴ _        5700e"^4,cos(35x + 95 Q _ 61635e"^4,sin(35x + 95Z)

^ичастн — 24    8           17461481                   34922962

_ 5700 e~^4zcos(105x + 285 Q 185545 e~^{4 z}sin( 105x + 285/) 1382276281                   2764552562

> #Определяем начальные и граничные условия для v(x,t)

> vtOx — ft Ox — и

J        части t = 0

>

vtOxf — ftOxf —

d

— и d i части

t = 0

> my PDF v — —yv^x, Z) = a² -Laplacian(v{x, t), [xl) : '                d/²

> my_solve_v — pdsolve^myPDF _v)

my_solve_v — v = _Fl(2t + x) + _F2\2t — x)

> #Ищем функции f= _F1 (x) и g =_F2(x) no формуле Даламбера

>            1

> my mt := ——

"            z-a vtOxf dr: 0

> Д1Д

'       2

+ myjnt

f — 2cos(49x)

75 sin(35x) cos( 105 х)	25 sin( 105 x) 315896	85622091605384	sin(3x) 3
35896       236922		506868411366075381
vtOx           . . > g •—       my_mt
, .„ ,    5sin(47x) . 8х3	107x2	x4 ! x5 ! 3 cos(35x)
5                       2          3	4	48    16     381374
495 sin(35x) cos( 105x)	165 sin( 105x	)      85622091605384
1525496      10291722 sin(3x) 3	13722296	506868411366075381

> v — subs^x = x + a-t,f) + subs^x = x — a-t,g^

5 sin(47x) 4x³ _ 101 x² x⁴ x⁵ _ 3 cos(35x)

2         3       4   + 48 + 16      8974

, = 2cos(98, + 49 ,) - ^i^M ₊ 4(2, + x)³ _ 101 (2^+,)=

(2 Z + x)4    (2 Z + x)5    3 cos(70 Z + 35x) 75 sin(70z + 35 x)

48          16    "      8974              35896

cos(210z + 105x)

25 sin(210z + 105x)

sin(6z + 3x) , _    ,,

H---—------ + 2 cos(49 x - 98 Z)

5 sin(47x — 94 z) 8(x-2z)³ _ 107 (x-2z)²    (x-2z)⁴    (x-2z)⁵

2                 3               4              48            16

3 cos(35x — 70 z) _ 495 sin(35x — 70 z) _ cos( 105x — 210z)

381374             1525496            10291722

165 sin( 105x — 210z) sin(3x — 6z)

13722296      "      3

> #Возвращаемся к исходному решению

> ту solve и '■= v + и

7 —    —           части

,         х⁵ X⁴ , 5700e”^4/cos(35x + 95/)    61635 e"^4z sin(35x + 95 Л

-      8    24           17461481                   34922962

_ 5700 e ⁴'cos) 105x + 285/)     185545 e ⁴'sin( 105x + 285/) sin( -3x + 6 /)

1382276281                   2764552562                  3

+ 2 cos( -49 , + 98/) + Ssm(-47, + 94/) 3_Cos(-35, + 70/) ’            2                  381374

495 sin( -35x + 70 t) cos( - 105x + 210 /)     165 sin( - 105x + 210/)

1525496      "     10291722     "       13722296

+ 2,05(98, + 49,) - Ss.n(94, + 47,) ₊ 4(2/ + ,)’ _ 101(2^+,)’

(2 / + x)⁴    (2 / + x)⁵ _ 3cos(70/ + 35 x) 75 sin(70/ + 35 x)

48          16             897435896

cos(210/ + 105x)    25 sin(210/ + 105x) sin(6 / + 3x)    8 (x — 2/)3

236922      "       315896               33

_ 107 (x-2/)² (x - 2 /)⁴    (x-2/)⁵

4              4816

• >    ^Проверка решения

• >    dtt_my_solve_u — simplify

  —— my solve и dr '

  
  

  dtt_my_solve_u —

  
  

  -416 + 96x — 64/—

  
  

  27930000 e"⁴ *cos(35 x + 95 /) 17461481

563933715 e"4' sin(35 x + 95 /)    251370000 e"4 f cos( 105 x + 285 /)

34922962                       1382276281

15093915905 e"4z sin( 105x + 285/) 2764552562

+ 2x~ + 10x3 + 8 Г + 120 /2х — 12 sin( - 3x

1050cos(-35x + 70 f) 27241

+ 6/) - 19208 cos(-49x + 98/) - 22090 sin(-47 x + 94 1) -

86625sin(-35x + 70/)    1050 cos(-105x + 210/)

54482                   245041

, 259875 sin( - 105x + 210/)                                                 ,

H-- 490082 ----------- 19208cos(98 / + 49x) + 22090 sin (94/ +47 x)

1050cos(70/ + 35x) _ 13125sin(70/ + 35x) _ 1050cos(210/ + 105x)

641                    1282                     5641

39375 sin(210 / + 105x)

12 sin(6/ + 3x)

d2

• >    dxx_my_solve_u — ——my_solve_u dx²

,        ,                           6982500e"4,cos(35x + 95 О ахх ту solve и := -104 + 24 х — 16 t —---------тттттттт:---------

-       -                                17461481

75502875 e"4,sin(35x + 95 Q 62842500+4' cos( 105л- + 285Q

34922962                      1382276281

2045633625 е~4 ?sin( 105х + 285 Q

^-----3 sin( - 3 х + 6 О — 4802 cos(

11045 sin(-47x + 94Q _ 525 cos(-35х + 70 Q

2                    54482

86625 sin(-35x + 70Q    525cos(-105x + 210Q

217928                 490082

+ 259875 sm(-105x +210 0 _ 48Q2 cos(98 f + 49 x) + 11045 sin(94 / + 47x)

5 (2/+x)³    (2/+x)²    525 cos(70 / + 35x) _ 13125 sin(70/ + 35x)

4            4              1282                  5128

525cos(210? + 105x) 11282

39375 sin(210/ + 105x)

— 3 sin(6/ + 3x)

5 (x — 2 I)¹ (x — 2 Q~

4     ~

> simplify(subs(t = 0, my_solve_u^)

4cos(49x) — 5 sin(47x) + 4x3 — 52x2

> simplify subs / = 0,

d ,

---my solve_u d t

4cos(3x) — 8x2 + 6x

> simplify^ dtt_my_solve_u

— a"-dxx_my_solve_u — myj\x, t))

>

plot3d\ my_solve_u,x=-

n

Л „ я

..---,/ = 0..—

32        8

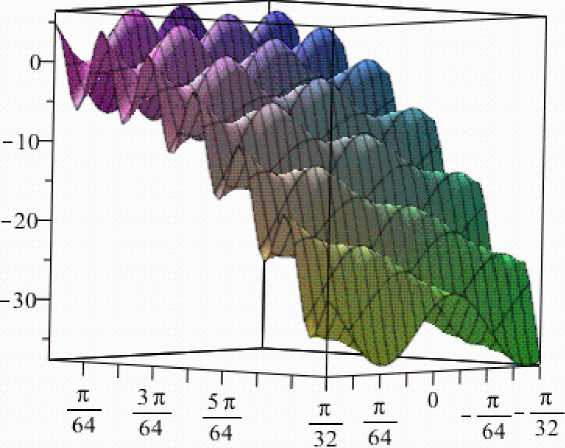
Рисунок.

Заключение

В статье был продемонстрирован подход, который можно применять во время обучения методам и инструментарию ком- тической физики. Представленный исходный текст на Maple можно легко модифицировать, что способствует лучшему закреплению обучающимися предлагаемого пьютерного моделирования для аналити- материала.

ческого решения уравнений задач матема-