Реализация фильтра повышения резкости в системе остаточных классов на FPGA

Повышение резкости изображений находит свое применение в различных отраслях – от цифровой печати до технического контроля в промышленности и систем военного назначения [1]. Аппаратная реализация фильтрации видеоизображений является важной прикладной задачей, для эффективного решения которой применяются различные программно-аппаратные методы и алгоритмы. Одним из способов введения параллельности вычислений является использование системы остаточных классов (СОК).

Фильтры повышения резкости

С математической точки зрения повышение резкости может быть достигнуто пространственным дифференцированием, которое усиливает перепады и разрывы изображений и не подчеркивает области с медленным изменением уровней яркости. Простейшим изотропным оператором, основанным на производных и применяемым для повышения резкости, является лапласиан [2]

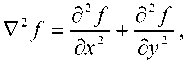
где для частной второй производной используется формула

= Дх + !^)+ Дх - v у)~1Дх, у), ох"

где f(x, у) – значение яркости изображения в точке с координатами .

Применение оператора Лапласа выделяет разрывы уровней яркости и подавляет области со слабым ее изменением. В итоге получается изображение с темным фоном, содержащее сероватые линии на месте контуров и других разрывов. Для получения изображения с увеличенной резкостью необходимо из исходного изображения вычесть его лапласиан, то есть где                – исходное изображение и изображение с повышенной резкостью. Подставляя в оператор (2) лапласиан (1) и определение второй частной производной, получим

g(x,y)= Дх, j) - /(х + 1, у) - /(х - 1, j) +

+ 2/(х, у^ - Дх, у +1) - /(х, у -1) + 2/(х, у) =

= -Дх - L у) - Дх, у -1) + 5/(х, у) -

-/(х,у + 1)-/(х + 1, у).

Запишем полученные коэффициенты в виде матрицы, тогда

'         -f^-ty)         '

~Дх, ^-1)   5/(х, у) -/(х, v + 1) , ч            -/(x + l,v)            ?

или, задавая (2) в виде маски, получим

'О -1 0Л

-1 5 -1

<° -1 Д

Включение диагональных направлений в формулу (2) позволяет дополнительно увеличить резкость и приводит к маске

'о -1 o'

-1 9 -1 .° “' °>

Применение маски к исходному изображению является поэлементной операцией и выполняется по-пиксельно. Рассмотрим в качестве примера применение маски к фрагменту изображения с размерностью равной размерности маски. Результатом такой операции будет значение результирующего пикселя.

' 15	10	3 л		' 0	-1	0^
2	4	16	*	-1	5	-1	=
J30	210	200?		V0	-1	0 V

= 150 + 10-(-1)+3-0 + 2-(-1)+4-5 + 16-(-1) +

+ 230 • О + 210 • (-1)+ 200 ■ О =

= -10-2 + 20-16-210 = -218.

Так как диапазон значений пикселей равен [0,255], то все значения меньше нуля округляются до нуля, а все значения больше 255 – до 255. Таким образом, результатом вычислений будет значение пикселя равное 0.

Система остаточных классов

Большое количество исследований посвящено поиску эффективных средств цифровой обработки изображений, среди которых выделяется применение системы остаточных классов [3-4]. СОК определяется набором положительных взаимно простых модулей Ц, т, ,...,№„}, и любое число Хе[о, М-1], где М = р^ т_; – динамический ;=1

диапазон, однозначно представляется упорядоченным набором остатков kx_v,X,,...,X_n\ где х, = X mod т_{ . Для представления отрицательных чисел динамический диапазон разбивается на равные части, и можно однозначно представить любое число X , удовлетворяющее одному

М-1 из выражений

М-1

при нечетном

М и -—<Х< — -\ при четном м [5].

Проблема выбора набора модулей особо актуальна при аппаратной реализации цифровой обработки изображений. Так, в [6] в качестве набора модулей взят набор Ь""1 +1,2" -1,2"} при и = 3, то есть {5, 7, 8} с динамическим диапазоном М = 280 – это мотивируется тем, что значения пикселей расположены в диапазоне от 0 до 255, что входит в диапазон [0, 280) . В качестве маски используется оператор Лапласа, заданный матрицей (4). Однако в [6] не учитываются случаи, когда на вход подаются матрицы

<255 255 255) <0 о

255   0   255 и 0 255

(255 255 255) (О О

О' О 0?

тогда результаты будут -2040 и 2295 соответственно, или, округляя по правилам фильтрации, 0 и 255. Если рассмотреть данный пример в СОК, получим (0, 4, 0) и (0,6,7), или, в позиционной системе счисления, 200 и 55. Данная ошибка связана с переполнением диапазона. Чтобы избежать этого, необходимо вычислить минимальное и максимальное значения, которые для фильтра (4) (-1)-8-255 = -2040 и 9-255 = 2295. Тогда минимальный динамический диапазон должен быть равен [О, 4590) , и очевидно, что набора модулей {5, 7, 8} не хватает.

Приближенный метод определения знака и восстановления числа

Если при выполнении сложения и умножения преимущества системы остаточных классов очевидны, то выполнение немодульных операций, таких как определение знака, переполнения диапазона, сравнение чисел, является проблемным [7]. В [8-9] показан приближенный метод сравнения чисел в СОК, основанный на использовании относительных величин анализируемых чисел к полному диапазону, определяемому Китайской теоремой об остатках (КТО) [10], согласно которой позиционное число определяется выражением:

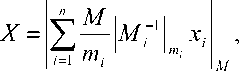
где М,. = — и М’¹ – мультипликативная ин ' 1ТЦ ^{1          1}

версия м, относительно т.. Если левую и пра- вую части выражения (5) разделить на величину м , то получим приближенное значение

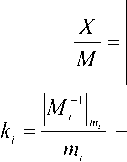
константы выбранной СОК.

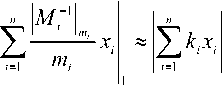
Для восстановления числа умножим (6) на м . В отличие от восстановления числа с помощью КТО, в данном методе нет необходимости находить остаток по большому модулю м . Чтобы определить знак числа , воспользуемся следу-

X 1

ющим правилом: если , то число положи- X 1 М 2

тельное, если , то число отрицательное.

Таким образом, мы имеем весь математический аппарат как для десятичной системы, так и для системы остаточных классов, чтобы реализовать выполнение фильтра повышения резкости.

FPGA реализация фильтра повышения резкости

Моделирование фильтрации изображения с помощью маски (3) было проведено на FPGA Xilinx Kintex 7 XC7K70T, на вход которой подавались 8-битные числа со значениями пикселей изображения в оттенках серого. Так как хранение всего изображения размерности MxN в LUT’ах FPGA занимает значительную площадь, нами был использована FIFO-структура размерности 2N + 2M - 3 бит. Докажем достаточность данного числа.

Для первого выполнения фильтра необходимо иметь в памяти 2N + 3 значений пикселей (первые две строки и количество столбцов фильтра). После выполнения фильтрации первой строки изображения, при переходе на вторую, необходимо накопить дополнительно два пикселя. Всего таких накоплений будет М-3 . Перемножая и складывая следующие величины, получим 2N + 2M-3 бит.

В качестве системы оснований была выбрана система вида {2" -1, 2",2"⁺¹ -1} при /7=4, то есть {15,16,31}, c динамическим диапазоном М = 7440 . Данный набор выбран в связи с относительной простотой аппаратной реализации операции нахождения остатка от деления по данным модулям. На вход FPGA также подавались 8-битные числа, которые после блока перевода в СОК заполняли две FIFO-структуры, содержащие 4-битные числа, и одну, содержащую 5-битные числа.

Далее процесс фильтрации проходил по трем параллельным потокам по модулям 15, 16 и 31, после чего данные поступали на блок сравнения и восстановления числа. Для определения позиционной характеристики была использована формула (6). Поскольку аппаратная реализация рациональных чисел весьма проблематична, константы были умножены на 2 , где X = Plog2 цМД – наименьшее значение, при котором восстановление позиционной характеристики из представления в СОК будет корректным [9], M^^L^i-^V м – динамический диапазон. Тогда после умножений и сложений в формуле (6) берется остаток по модулю 2 . Для определения отрицательных чисел было проведено сравнение с 0.5 -2N, а для определения выхода за 255 – сравнение с 17969, что соответствует значению, полученному по формуле (6) для числа 255 и умноженному на 2- .

Результаты моделирования

Для моделирования была использована FPGA Xilinx Kintex 7 XC7K70T и стандартное изображение Lena с разрешениями 64x64, 128x128 , 256x256,, 375x375 и 512x512. В качестве критериев оценки были использованы максимальная частота работы схемы и количество использованных слайсов.

Результаты моделирования показаны в таблице 1. Стоит заметить, что этап трассировки СОК реализации для изображения 512x512 закончился с ошибкой из-за большого числа сигналов.

Таблица 1. Результаты моделирования фильтрации

	Количество используемых слайсов	Максимальная частота работы, МГц
64x64	1862	80
128x128	3716	76
256x256	7946	75
375x375	10054	73
512x512	10180	72

Заключение

Таким образом, в работе показана применимость СОК для задач фильтрации изображений. Показаны критерии выбора динамического диапазона, введена FIFO-структура определенного размера, что повышает эффективность использования FPGA. Применение приближенного метода сравнения чисел позволяет улучшить скорость работы по сравнению другими методами. Моделирование на FPGA Xilinx Kintex 7 XC7K70T позволило определить необходимые аппаратные затраты для представленных разрешений изображений.

Работа выполнена при поддержки базовой части государственного задания СКФУ №2563.