Реализация национальной образовательной инициативы "Наша новая школа"

В национальной образовательной инициативе «Наша новая школа» одной из главных задач современной школы выделяется раскрытие способностей каждого ученика. Также отмечается, что школьное обучение должно строиться так, чтобы выпускники могли самостоятельно ставить и достигать серьёзных целей, умело реагировать на разные жизненные ситуации. В настоящее время работники системы образования на разных уровнях осуществляют непрерывный поиск путей достижения поставленных целей. Основным является совершенствование системы образования, причем сразу по нескольким направлениям: содержание обучения, методика преподавания, современные педагогические технологии, система оценивания и контроля знаний учащихся, внеурочная деятельность учащихся. Не рассматривая другие направления, остановимся только на возможностях внеурочной деятельности учащихся в достижении поставленных целей.

Внеурочных форм работы существует достаточно много, и практически все они в разное время разрабатывались специалистами в области математики и методики её преподавания. Эти исследования и разработки подтверждают идею о том, что, совершенствуя систему внеурочной деятельности учащихся, мы имеем широчайшие возможности развития и модернизации всей системы образования. Разнообразных материалов по отдельным формам внеурочной деятельности учащихся в настоящее время имеется очень много. Однако перегруженный должностными обязанностями и множеством разнообразных проблем учитель зачастую не имеет возможности разбираться в огромном потоке не всегда должным образом систематизированных материалов по внеурочной деятельности учащихся. Вследствие этого не всегда учителя используют тот богатейший опыт, который имеется.

Все формы внеурочной работы мы условно разделили на три группы: обучающие (кружковые и факультативные занятия, занятия творческой мастерской, учебноисследовательская работа и др.), занимательные (игры, математические вечера, конкурсы и др.) и контролирующие (олимпиады различного уровня, разнообразные конкурсы, например, «Кенгуру», и др.). В дополнение следует заметить, что на современном этапе стало актуальным использование не отдельных форм внеурочной деятельности учащихся, а объединение их в единую систему.

Вышесказанное обуславливает актуальность нашей работы, которая состояла в разработке программы обучающих внеурочных занятий по математике и полный комплект учебно-методических пособий к этой программе, обеспечивающий учителя всеми необходимыми материалами для организации системы работы с учащимися 5-7-х классов. Основными целями такой системы внеурочной деятельности являются следующие:

Работа удостоена Гранта Москвы в сфере образования в 2010 году.

• V    более глубокое и осмысленное усвоение программного материала;

• V    подготовка к изучению систематических курсов алгебры и геометрии;

• V    формирование и развитие устойчивого интереса к математике и её приложениям;

• V    стимулирование развития математических способностей;

• V    воспитание культуры математического мышления;

• V    расширение и углубление представлений о практическом значении математики, математическом моделировании, культурно-исторической ценности математики;

• V    формирование умений и навыков работы с учебной и научно-популярной литературой;

• V    привитие вкуса к самостоятельным творческим занятиям математикой и потребности в них.

В соответствии с поставленными целями программа включала в себя следующие тематические блоки:

Числа и нумерация: История возникновения чисел и способов их записи. Римские цифры. Натуральные числа и действия над ними. Обыкновенные дроби и действия над ними. Десятичные дроби и действия над ними. Положительные и отрицательные числа и действия над ними. Рациональные числа и действия над ними. Другие системы счисления: шестидесятиричная и двоичная. Действия в двоичной системе счисления.

Геометрическая линия: Решение геометрических задач на разрезание и перекраивание. Оригами. Угол. Треугольник. Куб и прямоугольный параллелепипед. Изготовление каркасов. Развертки.

Занимательная математика: Математические софизмы. Секреты некоторых математических фокусов.

Решение задач: Метод максимального предположения. Метод «с конца». Метод ложного положения. Сюжетные задачи. Задачи на совместную работу. Задачи на среднее арифметическое, среднюю скорость, среднюю цену. Задачи на проценты. Задачи с числами. Задачи на прямую и обратную пропорциональность.

Элементы теории логики: Решение логических задач с помощью таблиц. Элементы теории графов. Применение графов к решению логических задач. Логические игры. Математические игры и стратегии.

Делимость: Решение задач с использованием четности чисел. Задачи на делимость чисел. Признаки делимости с доказательством. Делимость и остатки. Задачи на НОД и НОК. Диофантовы уравнения и их решение.

Элементы теории множеств: Понятие множества. Равные множества, пустое множество, подмножество. Число подмножеств данного множества. Операции над множествами. Пересечение (произведение) множеств. Вычитание. Дополнение к множеству. Объединение множеств (сложение). Круги Эйлера. Формула включений и исключений. Числовые множества. Числовые промежутки.

Комбинаторные задачи и теория вероятностей: Принцип Дирихле. Правила произведения и суммы. Перестановки. Размещения. Сочетания. Факториал. Понятие вероятности события.

Функциональная линия: Функция y = kx + b и ее график. Построение части графика функции на промежутке. Кусочные функции. Модуль числа. Геометрический смысл модуля. Функция y = | х | и ее график. Построение и преобразование графиков. Графический метод решения уравнений и неравенств.

Уравнения и неравенства. Разложение на множители: Линейные уравнения, содержащие параметр. Графический метод решения уравнений с модулем. Уравнения с модулем, содержащие параметр. Системы линейных уравнений. Системы линейных уравнений, содержащие параметр. Определитель второго порядка. Решение уравнений второй и третей степени с помощью формул сокращенного умножения. Квадратные уравнения, как математические модели реальных ситуаций. Применение формул сокращенного умножения в задачах на доказательство.

Остановимся подробнее на указанном учебно-методическом комплексе. Поскольку учебно-методический комплекс к программе призван предоставить учителю математики весь необходимый материал для организации системы внеурочной математической работы, то он включает в себя:

• 1.    Комплекс дополнительных, занимательных материалов по математике и подборку задач к ним для проведения занятий математического кружка в 5-7-х классах. Математический кружок является одной из самых значительных форм внеурочной деятельности учащихся, поскольку: во-первых, кружковая форма работы является доступной для всех школ, так как ее реализация не требует больших материальных затрат и специального оборудования и позволяет охватить достаточно большее количество учащихся; во-вторых, по форме проведения кружковые занятия являются схожими с урочными, но они имеют больше возможностей, по сравнению с урочными занятиями, в приобщении учащихся к новым формам работы (деловым и ролевым играм, лекциям, лабораторным и практическим работам и др.); в-третьих, посредством организации занятий математического кружка можно обеспечить функционирование системы внеурочной деятельности, оптимально учитывающее некоторые возрастные особенности учащихся 5-7-х классов. Поэтому большая часть материалов посвящена именно этой форме работы.

При выборе формы проведения занятия кружка с учащимися 5-7-х классов приоритет отдается комбинированному тематическому занятию, основную часть которого составляет разбор определенной темы и решение задач по этой теме. Помимо этого для проведения занятий используются следующие формы:

• 1)    «десятиминутка» – небольшое сообщение учителя или ученика по какому-нибудь сравнительно узкому вопросу, при выборе этой формы работы на занятии имеется возможность включать в занятие элементы учебно-исследовательской работы учащихся в виде сообщений;

• 2)    решение задач, не связанных с основной темой данного занятия;

• 3)    математические игры, иллюзии и развлечения, не связанные с основной темой заседания;

• 4)    разбор домашних задач;

• 5)    доклады на математические и историко-математические темы (на 20-25 мин);

• 6)    моделирование, практическая работа.

Первые занятия кружка играют очень важную роль. От того, как пройдут эти первые занятия, зависит многое. Именно на первых занятиях происходят организационные моменты, закладывается основа для формирования активного интереса и к кружку, и к математике. Определим два основных вопроса, которые требуют первостепенного решения при подготовке первого занятия кружка: привлечение на первое занятие учащихся и подбор соответствующей темы для его проведения.

Делать простое объявление с приглашением на занятие не целесообразно, лучше на одном из первых уроков предложить оригинальную задачу для решения. Затем пояснить, что решением таких и подобных задач, а также изучением некоторых интересных и полезных математических фактов и даже фокусов, которые не входят в программу общеобразовательной школы по математике, будет заниматься математический кружок и пригласить учащихся придти на занятие. На первое занятие целесообразно пригласить как можно больше учащихся, по ходу работы кружка все-таки часть учащихся по различным причинам перестанет ходить на занятия.

Материал для первых занятий кружка подбираются так, чтобы он был ясен и понятен учащимся, не вызывал неуверенности в своих силах; в то же время он должен быть интересным. Полезно использование исторического и занимательного материала. Наиболее удачным является проведение не одного, а серии первых занятий, посвященных одной тематике. Важно показать учащимся, что проведенные занятия не исчерпывают весь материал по данной теме, что он намного богаче и шире, предложить список литературы, рекомендуемой для расширения и углубления знаний по данной теме. Например, для проведения первого занятия кружка в 5-м классе вполне подходит тема «История возник- новения чисел и способов их записи. Римские цифры», а затем в продолжение ее несколько занятий по теме «Необычно об обычных натуральных числах». Тематика занятий позволяет использовать как богатый исторический материал, так и разнообразные дидактические игры. С первого же занятия начать приобщение учащихся к учебно-исследовательской деятельности. Для этого предлагается знакомство с одной из интереснейших книг [1]. Вместе с предложением почитать в названной книге статью «Арифметика каменного века» на с. 12-14, учащимся предлагается найти в статье ответы на вопросы и подготовить устный ответ на тот вопрос, который им больше всего понравился. Например, такие:

• 1.    Почему современные ученые смогли сделать вывод, что некоторые древние люди учились считать пятерками?

• 2.   Откуда пошло значение слова «бирка»?

• 3.   Как древние определяли, что каких-то предметов больше, а каких-то меньше?

• 4.   Как арифметика помогала древним земледельцам?

• 5.    Как древние скотоводы использовали первые арифметические знания?

На следующем занятии «десятиминутку» посвящают рассказам ребят о прочитанном в статье.

Занятия по теме «Необычно об обычных натуральных числах» перекликаются с изучаемым в этот момент в классе материалом . Основная цель кружковых занятий по данной теме: во-первых, на занимательном материале показать прикладную роль изучаемых разделов, во-вторых, формировать и развивать интерес к математике; в-третьих, глубже изучить строение десятичной системы счисления, как примера позиционной системы счисления.

Однако задачи, рассматриваемые на занятиях, имеют более высокий уровень сложности, поэтому необходима некоторая подготовительная работа. Полезно устно рассмотреть задачи на разложение числа по разрядным слагаемым, например:

• а)    представьте число abcd и число, полученное от перестановки его цифр в обратном порядке, в виде суммы разрядных слагаемых;

• б)    припишите к числу abcd справа цифру т и представьте полученное число в виде суммы разрядных слагаемых;

• в)    припишите к числу abcd слева цифру п и представьте полученное число в виде суммы разрядных слагаемых;

• г)    припишите между цифрами а и b числа abcd 0 и представьте полученное число в виде суммы разрядных слагаемых.

При решении задач на занятии следует учитывать, что иногда полезнее решить одну и ту же задачу несколькими способами, чем несколько подобных задач. При этом предпочтение отдается арифметическим способам решения.

На первом занятии можно предложить такое занимательное задание:

• •    В данном неверном равенстве переложите одну спичку так, чтобы равенство стало верным:

• а)                                                        в)

• б)                                                         ^г)

• 2.    Материалы для проведения практических занятий, которые используются в процессе проведения занятий творческой мастерской. Возраст 10-12 лет является самым благоприятным для развития «умных рук» (по В.А. Сухомлинскому). Организация деловой игры на занятиях кружка в 5—7-х классах с использованием элементов ручного труда позволит в непринужденной форме развивать способности выполнения таких логических операций, как анализ и синтез, прогнозирования результата, умения оценить результат и выполнить проверку его правильности. Такие занятия стимулируют формирование и развитие пространственного компонента, способствуют повышению мотивированного интереса к предмету и прикладной значимости математических знаний.

При этом для решения задачи ребятам необходимо выдать счетные палочки (вместо спичек) чтобы они сложили данные равенства и попробовали разные способы перекладывания палочек ля получения решения задачи. Выполнение такого задания представляет собой небольшую практическую работу, которую выполняют ребята в рамках кружкового занятия.

Сначала полезно использовать на занятиях лишь элементы практической работы, пример которой показан выше. Со временем полностью в форме творческой мастерской. На таких занятиях представляются широкие возможности для проявления творчества и богатой фантазии каждого учащегося. Можно организовать работу творческой мастерской по изготовлению моделей оригами, разнообразных геометрических головоломок, разверток и моделей многогранников.

Например, на занятии по теме «Куб и прямоугольный параллелепипед, изготов- ление каркасов» учащиеся выполняют следующие практические задания.

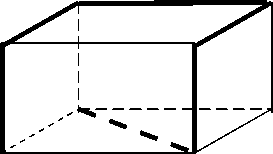
Задание 1 . Представьте стеклянный куб, на поверхности которого краской нанесены несколько линий, образующих в пространстве ломаную. На рис. 1 они выделены жирными линиями.

• а)    возьмите тонкую проволоку и изготовьте из нее мо-

• дель, соответствующую этой ломаной;                               Рис. 1

• б)    сделайте чертеж, представляющий собой вид изо

браженного куба с трех позиций: вид спереди, вид сверху, вид справа. Обозначьте вы- деленные линии.

Задание 2 . Имеется стеклянный куб, на поверхности которого краской нанесены несколько линий, образующих в пространстве ломаную. Даны изображения этого куба с трех позиций: вид спереди, вид сверху, вид справа (см. рис. 2).

• а)    начертите куб и покажите на нем, как проходит эта ломаная;

• б)    возьмите тонкую алюминиевую проволоку и изготовьте из нее модель, соответствующую нанесенным линиям.

  Вид спереди

  
  
  
  
  

  Вид справа

  
  

• 3.    Материалы для проведения факультативных курсов. Начиная с 6-го класса, полезным является использование еще одной формы внеурочной деятельности – факультативных занятий. Однако предложенные в работе материалы учитель может использовать по своему усмотрению: для проведения некоторых кружковых занятий или для проведения кратковременных факультативных курсов, например, в период школьных каникул.

Рис. 2

Такие задания требуют достаточно высокого уровня развития пространственного компонента математических способностей. Поэтому при определенных затруднениях учащиеся могут воспользоваться реальной моделью куба (можно заранее на предыдущем занятии ее изготовить). В задании 2 можно попробовать сразу выполнить пункт б), не выполняя задание а), что значительно усложняет задачу.

В 6-м классе предлагаются следующие темы для факультативных занятий: 1) «Решение некоторых задач с параметром»; 2) «Решение задач с помощью перевода числовых данных в другую систему счисления»; 3) «Эти загадочные проценты».

Факультатив «Решение задач с помощью перевода числовых данных в другую систему счисления» можно использовать в продолжение соответствующих кружковых занятий или на весенних каникулах. На занятиях рассматриваются следующие основные темы:

• 1.    Другие системы счисления. Перевод из недесятичной системы в десятичную и обратно.

• 2.    Действия в различных недесятичных системах счисления: сложение и вычитание.

• 3.    Действия в двоичной системе счисления: умножение и деление.

• 4.    Действия в различных недесятичных системах счисления: умножение и деление.

• 5.    Применение различных недесятичных систем счисления к решению задач.

• 4.    Материалы для организации учебно-исследовательской работы учащихся. Начинать учебно-исследовательскую работу с учащимися следует уже с 5-го класса. Такая деятельность учащихся может быть реализована в различных формах, например: 1) написание математических сочинений; 2) подготовка и написание доклада; 3) подготовка и написание реферата; 4) выполнение проектной работы (или части общей проектной работы).

Таким образом, начиная разговор с простого знакомства с другими позиционными системами счисления, и далее вводя действия в других позиционных системах счисления, мы имеем возможность добиться от учащихся более глубокого понимания структуры десятичной позиционной системы счисления, действий в десятичной системе счисления. А также знакомим учащихся с нетрадиционными методами решения задач, которые зачастую являются олимпиадными, а, в общем-то, достаточно легко решаются с помощью перевода числовых данных в другую систему счисления. Например:

Задача 1. Простым или составным числом является число (421 – 1)?

Задача 2. При каких целых положительных k число (3 ^k – 1) делится на 13?

Однако совершенно очевидно, что для достижения тех целей, которые стоят перед учебно-исследовательской работой учащихся, необходимо специально обучать некоторым составляющим ее умениям. В частности, умению читать учебную, научно-популярную и научную литературу. Для учащихся 5-го класса – это как раз та учебно-исследовательская деятельность, которую они могут выполнить. Ни в коем случае нельзя без специальной подготовки давать задания типа: «Написать математическое сочинение на тему …».

Пример одного из первых учебно-исследовательских заданий приведен выше. Учащимся 5-7-х классов предлагаются следующие задания:

• 1)    прочитать статью и найти в ней ответы на предложенные вопросы;

• 2)    прочитать статью и найти в ней ответы на предложенные вопросы. Подготовить небольшое выступление – ответ на самый интересный вопрос;

• 3)    прочитать статью и составить несколько вопросов, ответы на которые можно найти в этой статье;

• 4)    вопросы, составленные одним из учеников при выполнении задания 3, предлагаются другому учащемуся в качестве задания: прочитать статью и найти ответы на поставленные вопросы;

• 5)    обсуждение статьи учащимися, которые выполняли задания 3 и 4. обсуждение является свободной дискуссией, поэтому к ней могут присоединяться учащиеся класса, задавать вопросы, обсуждать выступления каждого из них;

• 6)    прочитать статью и составить аннотацию к ней. Аннотации должны быть тщательно продуманы, в них должно быть раскрыто содержание, в тоже время аннотация должна быть достаточно лаконичной, а после знакомства с ней должно появляться желание прочитать первоисточник.

• 5.    Методические рекомендации для учителей . Помимо предложенных материалов для проведения занятий комплекс содержит подробные методические рекомендации для учителя, как к конкретным темам, так и к отдельным задачам, а также по организации различных форма работы. Например, много вопросов вызывает принцип оценивания учебно-исследовательских работ. Мы предлагаем с критериальный принцип оценивания учебно-исследовательских работ. При этом система критериев должна соответствовать следующим условиям:

В процессе выполнения таких заданий учащиеся приобретают навыки чтения научно-популярной и учебной литературы, учатся выделять в ней полезную информацию по теме, своими словами формулировать мысли и передавать содержание. Подобные умения положительно начнут проявляться в последующем выполнении более серьез- ных работ, например, рефератов и проектов в старших классах, курсовых и дипломных работ в период обучения в высших учебных заведениях.

• 1)    быть четко определенной и заранее известной всем участникам;

• 2)    давать преимущество тем участникам, работы которых в наибольшей степени отвечают оптимальной стратегии развития научных способностей.

• 3)    носить скользящий характер, т.е. изменяться в зависимости от возраста участника, сохраняя при этом возможность сопоставления участников различного возраста между собой;

• 4)    результаты оценки работ по каждому из критериев должны быть известны всем заинтересованным лицам;

Выделим следующие критерии оценивания учебно-исследовательских работ: тип работы; наличие собственных оригинальных идей; наличие и характер анализа имеющейся по теме литературы; освоение учащимся новых методов или приемов; качество и практическая значимость исследования; оригинальность подхода и качество оформления работы, качество подготовленного выступления и ответов на вопросы. В зависимости от возраста каждый критерий будет коэффициент, по которому рассчитывается общий балл работы. Например, для учащихся 5-го класса более значимыми критериями оценивания работы будут: оригинальность подхода и качество оформления работы , качество подготовленного выступления и ответов на вопросы. По этим критериям соответствующие коэффициенты будут выше. А вот уже для учащихся 7-го класса повысится значимость критерия: освоение учащимся новых методов или приемов, вместе с этим повысится и его коэффициент.

Работа над комплектом учебно-методических пособий началась в 1995 году на базе средней общеобразовательной школы № 314 ВОУ г. Москвы (сейчас средняя общеобразовательная школа с углубленным изучением английского языка № 1352). В 2003-2005 годах они получили внедрение на кафедре методики преподавания математики в школе в Московском городском педагогическом университете; в 2005-2007 годах на кафедре методики преподавания физики и математики в Педагогической академии последипломного образования.

По материалам исследования: опубликованы статьи (Еженедельное учеб.-метод. прил. к газете «Первое сентября» «Математика». – 1998. - №№ 10, 16, 25; 1999. - №№ 39, 41, 42, 46; Научно-методический журнал «Математика в школе». – 2010. - № 3; сделаны доклады на Межвузовской научно-практической конференции в Москве (2002), VIII Всероссийском социально-педагогическом конгрессе в Москве (2008); Всероссийском методическом семинаре учителей математики и методики ее преподавания в Калуге (1998), в Брянске (1999), в Москве (2000), в Вологде (2001), в Санкт-Петербурге (2002), в Москве (2010); разработан спецкурс для студентов педагогических вузов с целью подготовки будущих учителей к организации внеурочной деятельности учащихся, который прошел апробацию в Московском городском педагогическом университете на кафедре методики преподавания математики в 2003-2005 гг. разработана серия лекций для учителей, которые читались автором в рамках курсов повышения квалификации на базе Педагогической академии последипломного образования (2005-2007).

* *    *

1. Виленкин Н.Я., Депман И.Я. За страницами учебника математики: Пособие для учащихся 5-6 классов средней школы. – М.: Просвещение, 1989.