Региональный индекс здоровья населения страны как фактор планирования системы медицинского обслуживания

В составляющих индекса развития человеческого потенциала (ИРЧП): материальное благополучие, здоровье и образование – важнейшую роль для российского населения играет уровень здоровья [3]. Это должно учитываться при планировании развития здравоохранения, управления его структурой и взаимодействием отдельных компонентов. На уровне страны индекс здоровья населения как компонента интегрального индекса качества и уровня жизни измеряется через ожидаемую продолжительность жизни при рождении [1], то на уровне регионов этот показатель качественно «не срабатывает». Здесь, помимо ожидаемой продолжительности жизни при рождении, необходимо учитывать показатели, отражающие воспроизводство населения – рождаемость, общую и младенческую смертность. Немаловажными являются также показатели заболеваемости, самым непосредственным образом определяющие трудовой потенциал региона. Система медицинского сервиса должна объективно отражать эти факторы, связывая их с численностью медицинского персонала и общих затрат по отдельным статьям.

Измерение уровня здоровья населения регионов

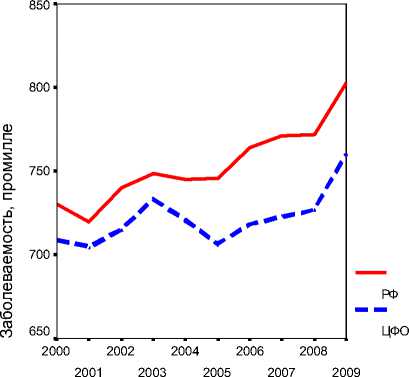
Состояние здравоохранения зависит не только и даже не столько от числа стационаров или мощности амбулаторных учреждений, сколько от их оснащенности современным оборудованием, а это, прежде всего, определяется объемами финансирования. Всемирная организация здравоохранения (ВОЗ) рекомендует тратить на медицину не менее 5 … 8% ВВП, а в России этот показатель не превышает 3%, что получает выход в финансировании всех субъектов РФ. На душу населения приходится финансирования в 40 раз меньше, чем в США, в 20 … 30 раз меньше, чем в странах Западной Европы, в 10 раз – Чехии, втрое меньше, чем в государствах Балтии. В стране имеется высокий уровень заболеваемости – порядка 730-800 промилле, причем в период 2000–2009 гг. (если не рассматривать кризисный и посткризисный периоды) наблюдалась тенденция к росту данного показателя (рис. 1).

а

Год

Б

Регион

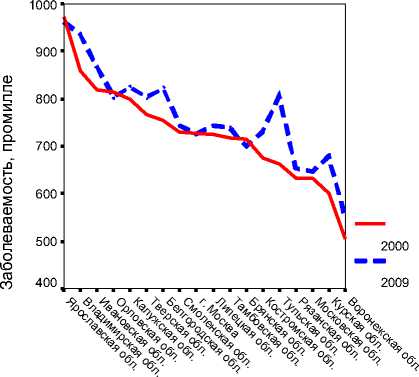
Рис. 1. Динамика заболеваемости в период 2000–2009 гг. в РФ и ЦФО ( а ) и дифференциация уровня заболеваемости по регионам Центрального федерального округа ( б ). Источник: [8]

Анализ временных рядов заболеваемости (рис. 1 а ), показал, что среднегодовой темп прироста заболеваемости в целом по стране в период 2000–2009 гг. составлял 0,97%, хотя в Центральном федеральном округе этот показатель был меньше (0,50%). Уровень заболеваемости существенно, практически в 2 раза различался и по отдельным регионам, от 500 промилле в Воронежской области до 950 промилле в Ярославской области (рис. 1 б ). Это актуализирует разработку регионального индекса здоровья как одной из важнейших составляющих интегрального показателя уровня жизни российского населения и фактора трудового потенциала, который бы учитывал различные стороны этого понятия.

Очевидно, что измерение уровня здоровья населения регионов должно учитывать значительно большее количество показателей, инициируя следующие задачи:

• 1)    отбор показателей, претендующих на включение в региональный индекс здоровья;

• 2)    выбор способа преобразования показателей в безразмерные частные индексы;

• 3)    определение формы объединения частных индексов в обобщенный индекс;

• 4)    расчет весов частных индексов.

В результате анализа литературных источников [3; 7; 8] в области исследования качества жизни населения, а также в области квалиметрии, сформулированы следующие положения к построению индексов уровня жизни населения территориальных образований:

• •    индекс должен быть безразмерной величиной, которая варьирует в открытом интервале от 0 до 1, асимптотически приближаясь к нулю в случае абсолютно неприемлемых значений образующих его показателей и к единице в случае очень хороших их значений;

• •    форма объединения частных индексов в обобщенный индекс должна устанавливаться, исходя из степени их взаимосвязи: при сильной корреляции частных индексов целесообразно использовать аддитивную форму   объединения,   при слабой их коррелированности –

мультипликативную;

• •    веса (приоритеты) частных индексов должны быть установлены либо экспертным путем, либо, что предпочтительнее, с учетом статистических характеристик реальных выборок региональных данных.

Отвергая естественное линейное нормирование на интервал изменения показателей, в качестве нормирующего преобразования предлагается использовать психофизическую шкалу Харрингтона [13]. Это ставит в соответствие значения формируемой на ее основе функции желательности лингвистической переменной с термами «очень плохо», «плохо», «удовлетворительно», «хорошо», «очень хорошо». В случае монотонности функции желательности, имеющей место для показателей качества жизни населения, шкала Харрингтона выглядит следующим образом (табл. 1).

Таблица 1

Числовые интервалы шкалы Харрингтона для монотонной функции желательности

Лингвистическая оценка (термы лингвистической переменной)	Интервалы значений функции желательности d ( x )
Очень плохо	0,00–0,20
Плохо	0,20–0,37
Удовлетворительно	0,37–0,63
Хорошо	0,63–0,80
Очень хорошо	0,80–1,00

При использовании шкалы Харрингтона для практических целей достаточно ограничиться тремя кластерами по лингвистическим термам «плохо», «удовлетворительно», «хорошо». Тогда оценке «удовлетворительно» соответствует зона 0,37–0,69 (табл. 1), «плохо» и «хорошо» характеризуются интервалами (0,00–0,37) и (0,69–1,00) соответственно.

Аналитически функция желательности Харрингтона [13]

di = d (zi) = exp (-exp (-zi)),                        (1)

zi = (хi – хi0)/( хi1 – хi0). (2)

Здесь zi – кодированные значения i-го показателя, представляющие собой безразмерные величины; хi – значение i-го информативного показателя; хi0 и хi1 – границы области «удовлетворительно» в исходной шкале di0 = d (zi (хi0)) = 0,368; di1 = d (zi (хi1)) = 0,692. (3)

Считая кодированное значение информативного показателя z=0 (нижняя граница области «удовлетворительно») функция желательности – 0,368. При z=1, (нижняя граница области «удовлетворительно»), d(z)=0,692. При построении функции желательности Харрингтона здесь надо установить границы исходных показателей хi0 и хi1, внутри которых изучаемая характеристика может считаться удовлетворительной. В частности, нередко эти значения полагают равными хi1=хmax и хi0=хmin, то есть соответственно максимальному и минимальному значению показателя по массиву региональных данных.

Такой подход ведет к тому, что все рассматриваемые статистические объекты в выборке считаются «удовлетворительными», тогда как это не является верным. Наоборот, всегда имеются как «лидеры», так и «аутсайдеры». Если нижнюю границу зоны «удовлетворительно» положить равной значению параметра какой-то центральной тенденции (медианы или средней арифметической величины), тогда ее верхнюю зону можно «сдвинуть» в сторону значений показателя, отстоящих от параметра центральной тенденции. Это среднее арифметическое показателей при нормальном распределении и медиана в других случаях равна величине стандартного отклонения (СКО в случае нормального распределения и трети межквартильного размаха в других случаях). Согласно правилу «трех сигм», используемому в подобных ситуациях [5], 1/6 часть статистических объектов будет характеризоваться термом «удовлетворительно», половина – термом «плохо», 1/3 – термом «хорошо».

Функция желательности тогда сигмоидальной формы и отвечает условию (1). Это означает, что начальный участок в графической интерпретации функции в зоне желательности «плохо» имеет нарастающую кривизну. Тогда даже незначительные изменения показателя приводят к заметному увеличению желательности, в зоне «хорошо» функция, наоборот, характеризуется убывающей кривизной. Поэтому дальнейший рост данного показателя уже не вызывает столь заметного увеличения желательности. В зоне «удовлетворительно» функция желательности практически линейна, и именно в этой области наблюдается максимальный эффект от увеличения показателя.

Сигмоидальный характер зависимости желательности от величины показателя отвечает следующей логике: на начальном этапе (зона «плохо») важно стимулировать рост показателя даже со значительными затратами ресурсов разного рода. Когда значения стр. 194 из 233 показателя уже устраивают (зона «удовлетворительно»), нет особого смысла в дальнейшем его росте до зоны «хорошо», резко увеличивая при этом затраты.

Используя такой подход и методику, можно обеспечить четкий типовой алгоритм построения региональных индексов. При этом преобразование исходных показателей с использованием психофизической шкалы Харрингтона позволяет производить экстраполировать результаты на расчеты частных индексов для территорий, ранее не включенных в обучающую выборку.

Следующие два важных аспекта измерения уровня здоровья населения регионов – установление математического вида обобщенного индекса и обоснование приоритетов (весов) частных индексов. Исходя из теории измерений, функции желательности являются в этом отношении «идеальными» математическими конструктами, поскольку они измерены в наиболее информативной абсолютной шкале и могут принимать любые значения в открытом интервале от 0 до 1. Как следствие, соответствующие этим функциям частные территориальные индексы можно агрегировать в обобщенные индексы различного вида.

Для выявления возможных способов объединения частных индексов в обобщенные обратимся к теории измерений: в многокритериальных задачах обобщенный критерий рекомендуется выбирать из семейства средних по Колмогорову, задаваемых монотонными функциями ψ согласно соотношению

F ^ψ n ( х 1 , х 2 , …, х n ) = ψ ^-1(1 /n ) Σ ψ ( х i ),               (4)

где ψ ^-1 – функция, обратная ψ ; х i – значение i -го показателя; n – объем выборки.

Выбор этих функций, как правило, осуществляется с привлечением суждений экспертов о связи обобщенного критерия с величинами частных функций желательности. Так, логично предположить, что совершенно неудовлетворительная ситуация по одному критерию ( d i ≈ 0) влечет за собой неудовлетворительную оценку ситуации в целом ( D ≈ 0). В математической форме это суждение находит свое отражение с помощью функций вида

ψ1 = ln d,(5)

ψ2 = -ln (-ln d).(6)

Соответствующие обобщенные критерии равны среднему геометрическому

D1 = DG = exp (Σ1/n* ln di) = (d1 d2 … dn)1/n(7)

и среднему логарифмическому

D1 = DL = exp [-(-ln d1) (-ln d2)… (-ln dn)1/n] .(8)

Если частные критерии неравноценны, то их весовые коэффициенты различны между собой, и обобщенные критерии имеют следующий вид:

D1 = DG = exp (Σ1/n* ln di) = d1α1 d2α2 … dnαn,(9)

D1 = DL = exp [-(-ln d1)α1 (-ln d2)α2… (-ln dn)αn],(10)

при условии

α1 + α2 + … + αn = 1.(11)

Сравнение критериев D G и D L показывает, что обобщенный критерий D G дает более жесткую оценку, чем D L : D G ≤ D L во всей области определения частных функций желательности.

Исходя из теории статистики, свертка частных критериев по формуле (9), то есть мультипликативная форма обобщенного критерия отвечает случаю отсутствия статистически значимой коррелированности частных критериев. Но это не всегда имеет место. Более того, практически во всех известных методиках расчета рейтинга неявно предполагается коррелированность частных критериев. Это выражается в аддитивной форме обобщенного критерия. Если частные критерии – функции желательности, то их аддитивная свертка производится по формуле

D адд = ( d 1 + d 2 + … + d n ) / n ,                (12)

в случае равенства весов частных критериев (то есть по формуле среднего арифметического) и

D адд = α 1 d 1 + α 2 d 2 + … + α n d n               (13)

в случае неравенства весов частных критериев α 1 , α 2 , … , α n .

Выбор конкретного вида свертки можно проводить по результатам факторного анализа частных функций желательности по методу главных компонент, суть которого состоит в выделении из множества главных компонент некоррелирующих между собой главных факторов, каждый из которых может коррелировать с одной или несколькими функциями желательности (соответственно, с одним или несколькими показателями [12]. Некоррелирующие частные функции желательности следует включать в обобщенный индекс в мультипликативной форме, коррелирующие – в аддитивной форме.

При выборе вида свертки частных функций желательности в обобщенный критерий, важной задачей является назначение весовых коэффициентов. Один из эффективных методов экспертного оценивания весов – метод аналитических иерархий, логические и алгоритмические основы которого рассмотрены в работах [4; 9]. Однако можно использовать и другой способ назначения весов – по результатам факторного анализа частных функций желательности, установив веса пропорциональными долям общей дисперсии, объясняемой соответствующими главными факторами.

Последующие исследования показали [11], что изложенные в статье методологические подходы к построению индикатора здоровья населения на региональном уровне позволяет избавиться от ряда недостатков существующих методик, использующих традиционные подходы (естественное нормирование при расчете индексов исходных показателей, допущение их равной значимости или априорное назначение весов), выявить болевые точки, производить расчет индикативных значений исходных показателей.