Regression Test Case Selection for Multi-Objective Optimization Using Metaheuristics

Travelling salesman problems is among combinatorial problems for optimization. TSPs with objective of minimizing the entire trip such a way –

• •    Visiting all the milestones (nodes) once.

• •    Return to initial (starting) node from where the journey started.

• •    Length (distance) of journey (trip) should be small.

TSP formula denoted as follow. Consider a network N= (M, A, P) where:-

• •    M –milestones set on the network.

• •    An arcs set.

• •    P= [ p ] , cost matrix

Simple application of travelling salesman problem is the visiting of a service boy around various locations while he is on duty, and wants to minimize overall travelling cost. The service boy faces routing problem, needed to schedule there visit for providing service to waiting customers by using already defined locations. Another TSP application is Post Routing. The postman is travels a defined number of addresses in their area. Also, the TSP acts as an important part of scheduling the trip of a postman, such that postman should travel a minimum path, the houses or milestones situated geographically apart to each other, to deliver each post and return to their initial location without visiting each location twice. Although, there are various other applications present such as:-

Also, applications on which TSP is used will never be explained by these few given examples, where as explained explanation on TSP application can be found in [A-B].

TSP as NP hard is proved in [1], which means an exact algorithm that is polynomial bounded for TSP exists unlikely. We proposed a heuristic algorithm in this paper for multi-objective optimization using metaheuristics to solve travelling salesman problem and their performance representation depend on TSP instances. This proposed algorithm was implemented and described by work in [2], [2] work available solution disintegrated to set of blocks that are overlapped to each other and after that blocks are individually explored. By using Generalized Crossing (GC) we done local searching, developed in [3], for TSP using genetic algorithm (GA), individual block is intensively explored for improving the existing solution. Proposed algorithm is then used for selecting optimal test cases, thousands of those test cases which are selected after confirming that they identify bugs and they itself selected from a repository of test cases; these thousand test cases are those test cases which are selected from several thousand test cases because they detect bugs. Few test cases from repository act as milestones (nodes) and having certain weight associated with each, proposed algorithm based on TSP implemented over selected result and select the optimal result or path or solution. These selected optimal test cases are further help to do regression testing, in order to remove most of faults or bugs effectively. Hence this proposed algorithm assures most effective solution for regression testing test case selection. Organized sequence of this paper is: Section 2, Literature review which defines the various works carried on the TSP, heuristic algorithm, genetic algorithm, multiobjective optimization, regression test case selection and metaheuristics.

Regression testing is carried out to ensure that changes and enhancements do not impact the previously working functionality of software. This testing is executed after enhancement on software environment and it is difficult to determine that how much re-testing is required, especially at the end of the development cycle (SDLC).

Multi-objective optimization is multiple criteria decision making procedure, which is concerned with mathematical optimization problems, including more than one objective function to be optimized simultaneously.

Metaheuristics is a higher-level heuristic designed to identify, generate a lower-level heuristic that is a goodenough solution to an optimization problem, especially with less computation capacity. Metaheuristics may make several assumptions to solve the optimization problem, and they may be usable for problems of variety.

Various software development leaders that are working to support number of software activities, where software testing activities require large number of costly resources. Hence, it is very important to use these resources judiciously. Efficient resources are required for testing of any software. Since for large software products, it is impossible to test all the classes completely as it is not cost-effective and it will be time consuming. Thus, we need to identify the classes and modules, where testing is actually required. I.e., we need to identify the classes and modules that are more prone to bugs. Those modules which are modified and also those modules having dependencies over these modified modules are selected for testing. When such modules are identified, we can focus on them to find the causes of failure. Thus, causes of failure will be useful and beneficial for saving time and resources during software testing to improve the software quality and reliability. There are number of software regression test case selection method was proposed in the literature [1], [2], [3], [4], [5], [6], [7], [8], [9] Also there have been various studies that have used subsets of the regression test case selection to analyzed relationships between the multi-objective and metaheuristics approach. Thus, paper provided the review and overview of all those previous studies from 2005 to 2014. These studies have been published in various conferences and journals ‘ACM Transactions on software Engineering and Methodology’, ‘Journal of Information Processing Systems’, ‘software quality journal’, ‘IEEE Transactions on software Engineering’, ‘Information and software Technology’, ‘Journal of Computer Science and technology’, ‘Empir software Engineering’, ‘Empirical software engineering’. In this study, we have focused on the techniques and efforts made and used by each study and the repository used to carry out the results. We mentioned the conference and journal name in which a paper has been published as well the year of publication for each one and their authors’ names. In all the studies on which the regression test case selection for multiobjective optimization with metaheuristics is used. Regression test case selection and its optimization is defined as the identification of fewer test cases from a large selected test case, which assures us to find the equal number of bugs that we found using large set of test cases. We have the complete summary of all the previous studies and work and thus comparative analysis can be performed.

Detailed proposed algorithm explained in sec (section)-

• 3.    Result of computation is provided in sec-4. Conclusion, future possibilities are written in sec-5.

• II.    Literature Survey

Construction procedures that are well known given here

• •    Rosencrantz and their team member [4] ; nearest neighbor procedure

• •    Wright and Clarke saving algorithms[5]

• •    Procedures for insertion [4]

• •    Karp [6]; partitioning approach

• •    Christofides [7] , various others ; minimal spanning tree approach ;

For TSP the best known iterative improvement algorithm is branch exchange and Genetic algorithm is providing the best solution for TSP under considerable environment. Lin [8] described the 2 opt and 3 opt heuristic. Quality of tours drastically improved by heuristic method, this is done by Lin and Kernighan [9]. In today scenario, their algorithm still acting as key ingredient of successful approaches in order to find high-quality paths (tour) and for other algorithm it always generate initial solution. [10] Gives an exchange procedure which is simplified requires o ( n ² ) operations at every stage, although produce a tour which is nearly better same as the medium performance of third optimization algorithm.

• •    Karp and Held[12]

• •    Smith and their team members [13]

• •    Eastman [14]

• •    Crhistofides [15]

• •    Carpaneto and Toth [16]

• •    Balas etc.

• •    Padberg and Crowder [17]

• •    Grötschel, Holland [18]

• •    Padberg, Hong [19] etc.

Also metaheuristic algorithm successfully applied to TSP by many researchers.

Simulated annealing algorithm were developed by

• •    Lo and Hus [20]

• •    Bonomi and Lutton[21]

• •    Nahar and their team member [23]

• •    Golden and Skiscim[22] etc.

For TSP metaheuristic algorithms such as Tabu search have been proposed by

• •    Fiechter[24]

• •    Knox[25] etc.

Ant Colony is a new metaheuristics algorithm, this was indicated by

• •    Bullnheimer and their team member [26]

• •    Banan and Gomez [27]

• •    Tsai and their team member [28]

• •    Dorigo and their team member [29] etc.

For TSP the genetic algorithm were reported by

• •    Whitley and their team member [30]

• •    Nguyen and their team member [31]

• •    Grefenstette and their team member [32] etc.

Techniques introduced for the TSP can be explained and elaborated in [A-B, 32] with comprehensive review. Further literature review for better understanding is illustrated in review paper of this topic i.e. Regression Test Case Selection for multi-objective optimization using Metaheuristics: a Literature Review.

• III.    Proposed Metaheuristic Algorithm

Here the proposed algorithm disintegrate existing path of TSP tour into overlapped blocks and all the blocks are focused and analyzed separately. Generalized Crossing (GC) method used for each block. The overlapping of each block enables us to modify position of milestones or nodes in the nearest block. Algorithm which is proposed in this paper utilizes a strategy called backtracking. When local optimum is reached by any block GC method is used to enhance that block. If in any circumstances GC method not able to enhance the block, the next block is selected and search for local optimum for enhancement. All this procedure is iteratively called till no block is present for the enhancement. Steps required in a strategy for above computation are minimized by:

If the node position between two blocks in overlap is changed then backtracking is implemented by Generalized crossing method, to take control to previous block to the current block; else the control transferred to next block from current block.

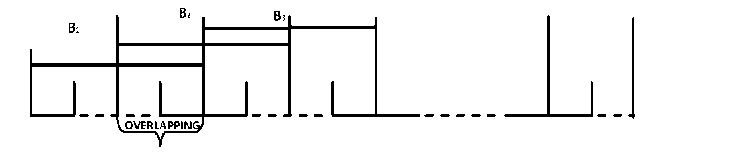
Fig. 1. overlapped blocks representation

According to above figure entire Travelling salesman problem route is disintegrated by implementing blocks (B1, B2, B3 …). Let we illustrate by an example GC locally search the local optima and enhance it, but again by implementing backtracking to B1 block local search is iteratively continued till no further improvement is needed or possible.

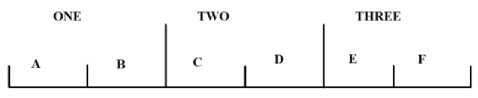
Fig. 2. block sequence at initial position

Let block size represented by sz and size of overlapped block represented by sz , sz was calculated by total nodes in block. sz_o is calculated by counting blocks that are overlapped to each other. Hence sz = 6, also we disintegrate block into 3 parts (one, two, three acc to figure 2). These three parts are used to create 5 new sequences. By using [3] these created sequences can further used to create new sequence, new sequences are in reverse order of the original. Now for every sequence in figure three, by reversing nodes we can create seven new sequences for one, two, three part represented in figure 2 and represent those seven sequences in figure 4. This means we are able to create forty-eight paths or tour on with initial tour is included. Initial enhancement strategy is first implemented using Generalized Crossing method.

ONE	THREE	TWO
|    A     | В	E 1'	c 1 D 1
TWO	ONE	THREE
C    D	A     В	E 1 E 1
TWO	THREE	ONE
1 c 1 D	E 1'	Л       В
THREE	ONE	TWO
1 E 1 F	A    В	c । D     ।
THREE	TWO	ONE
Iе l"	” 1 ”	A    В 1                                    1

Fig. 3.1 new sequences by rearranging original sequences

ONE	THREE	TWO
1 B 1 A	E 1 r	c 1 D 1
ONE	THREE	TWO
। A । В	Г , E	c 1 D 1
ONE	THREE	TWO
| A | B	E 1 "	D 1 c 1
ONE	THREE	TWO
1 A 1 B	F । E	D 1 c 1
ONE	THREE	TWO
1 B 1 A	F 1 E	D 1 c 1

Fig. 3.2 sequence by reversing the nodes in each part

This algorithm initiates its searching with small block with sz = 3, when there is no chance of improvement after few defined tries then algorithm terminates.

Now, for sz_B , if sz = sz_B . cofficient , number of disintegrated blocks from TSP path or tour gives by

nn

sz -sz sz .(1 - Coefficien t)

Where n is TSP size and ratio of sz / sz is called coefficient ( C ) 0 <  C ≤ 1 . The ability of termination when maximum trials are done to attain optimal solution or path if enhancement is not done after few steps, makes this algorithm faster as compare to other algorithm used for this purpose.

• IV.    Implimentation and Computation

Genetic algorithm to solve TSP problem is compared with the proposed algorithm i.e. modified genetic algorithm to solve TSP for local searching and enhancement of individual blocks. New algorithm executes 20 TIMES and for all the problems, the output and analysis is represented in below given Table 1. highlighted characters are the average deviation which is smallest between two algorithm.

Table having columns-

• •    Name of the problem

• •    Problem size

• •    tour optimal length L OPT

• •    %PDA –percentage deviation of average quality solution from L OPT

• •    %PDB –percentage deviation of best quality solution from L_OPT

• •    ACT –average time of computation.

• A.    Computation and comparision of proposed algorith with existing genetic algorithm.

The average deviation (AD) of proposed algorithm is .51774% and average deviation of existing algorithm is .52944%, hence the AD of proposed algorithm is smaller than existing algorithm. The proposed algorithm got 11 best solutions where as existing genetic algorithm got only 7 best solution, out of total 19 TSPs. And proposed algorithm average performance having 14 smallest values where as the existing genetic algorithm got 5 smallest values for the average performance. Although the time take by proposed algorithm is less as compare to existing algorithm but it is very difficult to compare because execution environment for both of the algorithm are very much different. In general our proposed algorithm is better than the existing genetic algorithm used for solving TSPs.

Table 1. New algorithm executes 20 TIMES and for all the problems, the output and analysis is represented in below

Problem Name Problem Size Optimal Solution TSP by Genetic Algorithm TSP by Proposed Algorithm %PDA %PDB TIME TAKEN (sec) %PDA %PDB TIME TAKEN (sec) A280 280 2579 0.31119 0.26099 1.73 0.30279 0.27685 1.40 Att48 48 10628 0. 4097 0.31500 1.09 0.36447 0.28499 1.45 Bayg29 29 1610 0.03557 0.02734 1.44 0.04847 0.03768 1.42 Berlin52 52 7542 0.23901 0.19806 1.57 0.24737 0.21314 1.45 Ch130 130 6110 0.40583 0.36240 1.52 0.39557 0.35267 1.74 Ch150 150 6528 0.48425 0.44806 1.67 0.48320 0.44418 1.74 Eil101 101 629 0.02986 0.02635 1.59 0.02965 0.02676 1.79 Eil51 51 426 0.01313 0.01065 1.38 0.01354 0.01114 1.36 Eil76 76 538 0.02161 0.01862 1.42 0.02108 0.01798 1.66 Fri26 26 937 0.02146 0.01521 1.45 0.02052 0.01474 1.58 Gr120 120 6942 0.45401 0.39840 1.61 0.43911 0.39342 1.61 Gr24 24 1272 0.02817 0.01987 1.56 0.02831 0.02143 1.40 Gr48 48 5046 0.18027 0.14607 1.62 0.17703 0.13917 1.50 Gr96 96 55209 3.18636 2.76012 1.46 3.09558 2.63036 1.57 kroA100 100 21282 1.40595 1.22245 1.40 1.38467 1.21503 1.12 kroD100 100 21294 1.36298 1.18006 1.51 1.32326 1.14852 1.58 Lin105 105 14379 0.99670 0.85149 1.69 0.99210 0.84577 1.67 Tsp225 225 3861 0.37662 0.34476 1.58 0.37443 0.34478 1.23 ulysses16 16 6859 0.09669 0.07484 1.53 0.09601 0.07249 1.18 AVERAGE 0.52944 0.44996 1.5168 0.51774 0.4469 1.4973 effective test case to perform regression testng. Figure

• B.    Implementation of proposed algorithm over the

selected test cases and identifing the minimal cost,         ^.

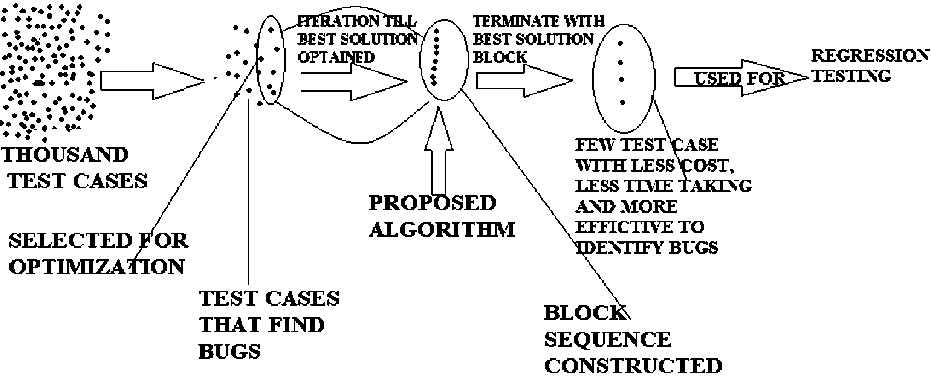
Fig. 4. overall representation of process activity

• V.    Conclusions

An algorithm is proposed to solve TSPs better than already existing genetic algorithm, both of these algorithm i.e. existing and proposed, are implemented to solve TSPs. Proposed algorithm is found better between both. Proposed algorithm used Generalized Crossing method and backtracking to optimize the block sequences and find out the best solution, where as GC implement the backtracking procedure iteratively till the best solution is not obtained, once a best solution obtained the algorithm terminates. This terminating property made the proposed algorithm better as compare to other algorithm. This proposed algorithm is then implemented selected test cases as shown in figure 4. Future accept of this paper is that if we can able to implement metaheuristics more coherently to prepare a new algorithm which is able to select the optimal test cases out of several thousand test case (they detect fault or bugs), then we are able to select those test case which identify bugs in very less time, cost effectively, and we can then find maximum bugs with these few test cases.

• VI.    References

  • [1]    Lawler E.L. Lenstra J.K., Shmoys A.H.G. D.B. and Rinnooy Kan, The TSPs. Ed. Chichester: John Wiley & Sons, 1985.

  • [2]    W.J. Cook, D.L. Applegate, V. Chvátal and R.E. Bixby, The TSPs: Princeton University Press, A computational study. Princeton: 2006.

  • [3]    Garey M.R. and Johnson D.S. , Computers-and intractability:   A   guide to   the theory of NP

    completeness.Freeman W.H., 1979.

• [4]    K.M. Ng,  S.B  Liu,  Ong  H.L.,“An overlapped

  neighborhood search method for general-sequencing problems,”, 2007.

• [5]    Ng K.M., Ong H.L., Zeng L., and “A-generalized crossing -local- search method for solving vehicle routing problems”, 2007.

• [6]    J. Wright, G. Clarke, “Scheduling of vehicles from a central-depot to a number of delivery-points”, 1964

• [7]    P.M. Lewis, Sterns R.E., and Rosenkrantz D., “An analysis -of several-heuristics for the TSP”, 1977.

• [8]    Karp R.M,“Probabilistic analysis of partitioning _algorithms for_the TSP _in_ the_plane,” Mathematics of Operations Research, 1977.

• [9]    Christofides N, “Worst case analysis of a new heuristic- for the TSP,” , 1976 February.

• [10]    Lin S., “Computer solutions of-the TSP”, 1965.

• [11]    B.W. Kernighan and S. Lin, and, “An -effective heuristicalgorithm for the-TSP,” 1973.

• [12]    Or I. “Traveling- salesman type combinatorial problems and their relation to the logistics of regional bloodbanking,” 1976.

• [13]    S.M Johnson, G.B. Dantzig, , S.M. and D.R. Fulkerson “SolutioN of a large scale TSP,” 1954.

• [14]    Held M., Karp R.M., “The TSP and minimum spanning trees”,1971.

• [15]    V. Srinivasan, G.L. Thompson AND T.H.C. Smith, “Computational performance of three subtour-elimination-algorithms for solving-asymmetric TSPs,” 1977.

• [16]    Eastman W.L. , “Linear-programming with patternconstraints,” , 1958.

• [17]    Balas E., Christofides N., “A restricted-lagrangean approach to the TSP,” 1981.

• [18]    Carpaneto G., and Toth P., “Some new-branching and bounding-criteria for the asymmetric TSP,” 1980.

• [19]    Crowder H. , and Padberg M.W. , “Solving-large scale symmetric TSPs to optimality,” 1980.

• [20]    Grötschel M. , and Holland O. , “Solution of -large scale TSPs,” Mathematical Programming, 1991.

• [21]    Padberg M.W., and Hong S., “On-the-symmetric TSPs: ,1980.

• [22]    Lo C.C., Hus C.C. , “An Annealing-framework with learning memory,” IEEE Transactions, 1998.

• [23]    Bonomi E., and Lutton J. L., “The N-city TSP: Statistical mechanics and the Metropolis-algorithm,” 1984.

• [24]    Golden B.L. , and Skiscim C. C. , “Using simulated annealing to solve routing and location problems,” 1986.

• [25]    Nahar S. , Sahni S., and Shragowitz E. “Simulated-annealing and combinatorial-optimization,” ijc Aided VLSI Design, 1989.

• [26]    C.-N. ,Fiechter, “A parallel tabu-search algorithm for large scale TSP,” Fédérale de Lausanne, 1990.

• [27]    Knox J., “An-application of TABU search to the symmetric TSPs,” University of Colorado, 1988.

• [28]    Hartl R.F., Bullnheimer B, and Strauss C., “An-improved ant system algorithm for the vehicle -routing-problem,” 1999.

• [29]    Gomez O. , and Banan B., “Reasons-of ACO's success in Traveling salesman problem,” Ant Colony Optimization And Swarm Intelligence, 2004

• [30]    Tsai C.W., Tsai C. F., Tseng C. C., “A new and efficient ant based heuristic method for solving the TSP,” 2003

• [31]    Colorni A., Dorigo M., and Maniezzo V. “The ant-system: optimization by a colony of cooperating-agents,” IEEE Transactions, Man and Cycbernetics, 1996.

• [32]    Fuquay D., Starkweather T., and Whitley D., “Schedulingproblems and tsp: The genetic edge recombination operator,” 1989

• [33]    Yoshihara I. ,Nguyen H.D., Yasunaga M. and Yamamori K. , “Implementation of an effective hybrid GA for large-scale TSPs,” IEEE Transactions on Systems, Man, and Cybernetic, 2007

• [34]    VanGucht D., Rosmaita B., Gopal R, and Grefenstette J.J. , “Genetic- algorithms for the TSP,” 1985.

• [35]    dehrui satchidananda and Ghosh Ashish. , 2005 march. Evolutionary algorithms for multi-creation-optimization: survey. International -journal of computing and information- sciences

• [36]    Antosiewicz Marek, Koloch Grzegorz, Bogumił Kamiński Warsaw School of Economics, ISSN 2299- 2634. Choice of best possible metaheuristic algorithm for the TSP with limited computational time: quality, uncertainty and speed. In Journal of Theoretical and Applied Computer Science, 2013

• [37]    Ciavotta Michele, Ruiz Rubén, , Minella Gerardo, March 2007:, A review- and- evaluation of multi-objectivealgorithms for the flowshop -scheduling problem, IEEE Transaction

• [38]    Thiele Lothar And Zitzler Eckart, Multiobjective Evolutionary-Algorithms: A Comparative Case-Study and the Strength-Pareto-Approach. IEEE Transactions, 1999

• [39]    Do Hyunsook & Rothermel  Gregg  & Kinneer

Alex,Prioritizing-JUnit-Test-Cases:     An Empirical-

Assessment and Cost- Benefits Analysis, Empir-Software-Eng (2006)

• [40]    Harman Mark and Yoo Shin King’s-College-London, CREST, Department of Computer Science Strand, London, UK

• [41]    L. GRAVES , Los TODD, HARROLD MARY JEAN, PORTER ADAM, KIM JUNG- MIN and ROTHERMEL GREGG,: An- Empirical- Study of Regression Test Selection Techniques, ACM Transactions on SoftwareEngineering and Methodology,” 2001

• [42]    ,Harman M. and Yoo S., Regression-Testing Minimisation, Selection and Prioritisation : A Survey, SOFTWARETESTING, VERIFICATION AND RELIABILITY, 2007;

• [43]    MELAB N., CAHON S., ParadisEO ,TALBI E.-G.: A Framework-for the Reusable -Design of Parallel and Distributed- Metaheuristics, Journal-of-Heuristics, 2004 Kluwer Academic Publishers. Manufactured in The Netherlands.