Регрессионный анализ показателей процесса замораживания дыни

Одним из основных направлений в области развития перерабатывающей промышленности является производство биологически полноценных продуктов длительного хранения, среди которых особую группу представляет продукция из бахчевых культур.

Бахчевые культуры, в частности дыня являются богатым источником многих жизненно важных для организма человека пищевых веществ, прежде всего витаминов, углеводов и минеральных веществ. Благодаря высокому содержанию сахаров, хорошим вкусовым свойствам и легкой усвояемости плоды дыни имеют особое место в пищевом рационе.

Характерной особенностью растительных клеток является наличие оболочек и клеточной влаги, занимающей место в протоплазме. Клеточную влагу можно рассматривать как водный раствор различных веществ. Молодые ткани содержат относительно большое количество воды и более упруги [1-2].

Во время медленного замораживания внутри клеток растительных тканей происходят осмотические и диффузионные процессы.

Образование льда начинается между клетками, вода диффундирует из них к кристаллическим зародышам, и клетки обезвоживаются, сморщиваются. Внутри клеток льда нет. При быстром замораживании образование кристаллических зародышей и кристаллов льда происходит внутри клеток, поэтому кристаллы льда вырастают еще до того, как наступит дегидратация клеток. Влияние скорости замораживания на растительную ткань проявляется не только в изменении гистологии, оно играет значительную роль в процессах, имеющих место при оттаивании замороженной дыни. При этом наиболее важным является вытекание сока, который содержит белки, аминокислоты, углеводы, минеральные вещества и витамины.

Количество вытекшего сока зависит от того, медленно или быстро проводился процесс замораживания. При быстром замораживании количество вытекшего сока меньше. Это объясняется тем, что в случае медленного замораживания ионная концентрация вследствие дегидратации клеток возрастает, поэтому при оттаивании растительная ткань не способна снова адсорбировать освободившуюся жидкость, так как денатурированные белки имеют пониженную способность к набуханию и удержанию воды.

Целью данной работы является установление взаимосвязи между выходными показателями процесса замораживания дыни и получение оптимальных параметров замораживания.

Объекты и методы исследований

Выбор полной квадратичной модели регрессии трех исследуемых параметров замораживания (температуры x 1 = t, скорости x₂ = и и продолжительности x₃ = т ) [1, 3]

P m = b 0 + b i x _i + b ₂ x ₂ + b ₃ x 3 + b n x 2 + b ₂₂ x 2

+ b ₃₃ x 2 + b ₁₂ x 1 x ₂ + b ₁₃ x 1 x ₃ + b ₂₃ x ₂ x ₃

обоснован тем, что взаимосвязи между потерей массы Pm и исследуемыми показателями замораживания во многих случаях, как показали однофакторные эксперименты (рис. 1), имеют нелинейный характер.

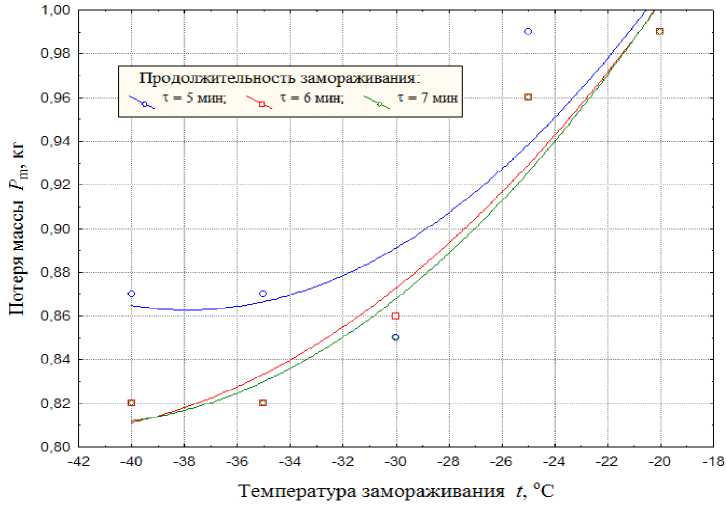
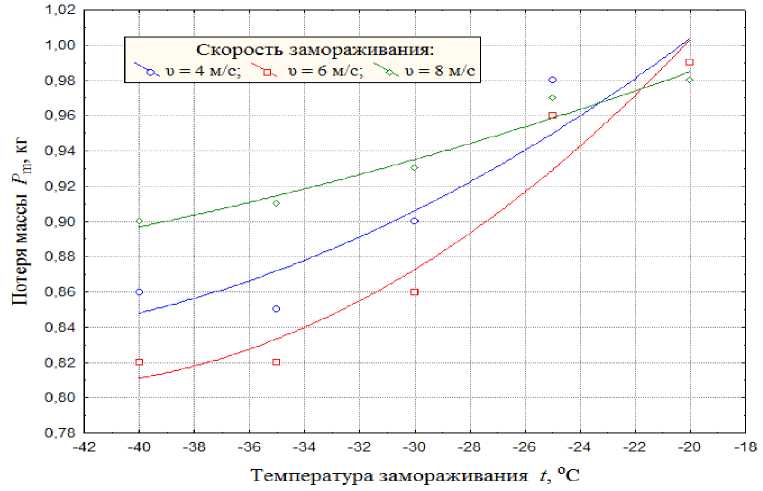
Рисунок 1 – Потери массы дыни в зависимости от температуры, продолжительности и скорости замораживания.

Для их адекватного описания в зоне эксперимента хорошо подходят полиномы 2-ой степени независимых переменных х 1 , х 2 и х 3 .

Полученные экспериментальные данные обработаны программой Statistica 7.0.

Для исследования влияния параметров замораживания на потерю массы продукции рассчитаны b-коэффициенты уравнения, их стандартные ошибки и 95%-ные доверитель- ные границы. Значимость параметров замораживания проверялась значениями t-критерия Стьюдента и рассчитанными уровнями p (таблица 1).

Результаты и их обсуждение

Произведя соответствующую замену переменных и подставив в (1) b-коэффициенты, получим следующее уравнение:

P m = 2,194 + 0,014278 t – 0,15833 υ – 0,1635 τ + 0,0002 t² + 0,009833 υ ² + 0,013333 τ ² – 0,00052 t υ +

+0,0012 t τ + 0,00425 υ τ

Таблица 1 – Регрессионный анализ показателей процесса замораживания

Обозначение		Коэффициент регрессии	Стандартная ошибка	t-критерий Стьюдента	p-уровень значимости	95 %-ные доверительные границы
						нижняя	верхняя
b 0	–	2,193778	0,358485	6,119583	0,000001	1,466015	2,921541
b 1	x 1	0,014278	0,007252	1,968731	0,056943*	-0,000445	0,029001
b 2	x 2	-0,158333	0,032275	-4,905795	0,000021**	-0,223855	-0,092812
b 3	x 3	-0,163500	0,103406	-1,581143	0,122841	-0,373426	0,046426
b 11	x 1 2	0,000200	0,000094	2,135704	0,039777**	0,000010	0,000390
b 22	x 2 2	0,009833	0,002078	4,733109	0,000036**	0,005616	0,014051
b 33	x 3 2	0,013333	0,008310	1,604444	0,117603	-0,003537	0,030204
b 12	x 1 x 2	-0,000517	0,000339	-1,522901	0,136768	-0,001205	0,000172
b 13	x 1 x 3	0,001200	0,000679	1,768531	0,085688*	-0,000177	0,002577
b 23	x 2 x 3	0,004250	0,002938	1,446504	0,156933	-0,001715	0,010215
Примечание: b i или b ii – линейный или квадратичный член регрессии; значимость на уровне: ** – p < 0,05; * – p < 0,1						b ji – парное взаимодействие;

Как следует из таблицы 1, на величину потерь массы Pm с уровнем значимости 0,05 (**) оказывают воздействие линейная составляющая скорости замораживания x2 =

2            2

xx υ и квадраты параметров: ¹ и ²

–

температуры (x 1 =t) и скорости (x 2 = υ ) замораживания. В группу факторов, оказывающих существенное влияние на показатель Pm с уровнем значимости 0,1 (*), вошли x 1 = t – температура замораживания и парное взаимодействие x 1 x 3 – температуры (x 1 = t) и продолжительности (x 3 = τ ) замораживания.

Оценка качества регрессионного уравнения (2) проверялась коэффициентом множественной корреляции R, детерминации R 2 , а также критериями Фишера F и Дарбина-Ватсона d. Полученные для уравнения (2) значения R = 0,914 и R 2 = 0,836 значимы и близки к предельной величине (R 2 ≤1), что свидетельствует о достаточно высокой тесной взаимосвязи исследуемых параметров с величиной потери массы при замораживании.

Рассчитанный критерий Фишера F = 19,799 характеризует значимость всего уравнения регрессии при соответствующем числе степеней свободы df 1 = 9 и df 2 = 35 и 95 %-ной доверительной вероятности, так как полученный статистический уровень (p = 3,01∙10-11) значительно меньше 0,05.

Критерий Дарбина-Ватсона d = 1,792 и малая величина незначимого коэффициента сериальной корреляции r = 0,078 подтверждают независимость полученных экспериментальных данных и то, что результаты предыдущих опытов не влияли на результаты последующих.

Таким образом, потерю массы продукции при замораживании в зависимости от исследуемых параметров достаточно полно характеризует рассчитанное уравнение регрессии (2). Значения статистических показателей и критериев показывают независимость полученных наблюдений, 95 %-ную достоверность уравнения и его адекватность процессу замораживания.

Для уравнения (2) определена оптимальная область регулируемых параметров замораживания t, υ и τ , вне которой снижение величины потерь массы продукции Pm не дает пропорционального эффекта. С этой целью построены поверхности отклика и линии равных уровней (изолинии) для величины потерь массы продукции Pm в зависимости от различных сочетаний исследуемых параметров замораживания: температуры t, скорости υ и продолжительности τ (рис. 2 - 4).

Справа от графиков находятся цветовые метки, по которым можно определить область значений регулируемых параметров замораживания, где функция отклика P m – потеря массы дыни имеет наименьшее значение. Чтобы найти это значение, была поставлена и решена следующая задача нахождения условного экстремума отклика Pm при ограничениях, накладываемых на параметры процесса замораживания:

• - найти минимум потерь массы дыни (кг).

P_m = f ( b ₁,..., b_k ; t , ϑ , τ ) ⇒ min

в области факторного пространства, т.е. при условиях, налагаемых на:

температуру замораживания oo min                   max           ,          (4)

скорость замораживания

ϑmin =4м/с ≤ϑ≤ϑmax= 8м/с и продолжительность замораживания

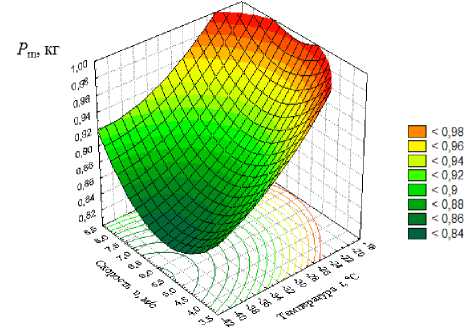
Рисунок 2 – Поверхность отклика и линии равных уровней потерь массы дыни в зависимости от

• τ _min = 5мин ≤ τ ≤ τ _max= 7мин. (6)

В поставленной задаче (3) – (6) в качестве функции P m использовано полученное ранее уравнение регрессии (2), min и max – соответственно нижняя и верхняя границы параметров замораживания.

Задача (3) – (6) решена в программе Excel 2003. Получены следующие оптимальные параметры процесса замораживания:

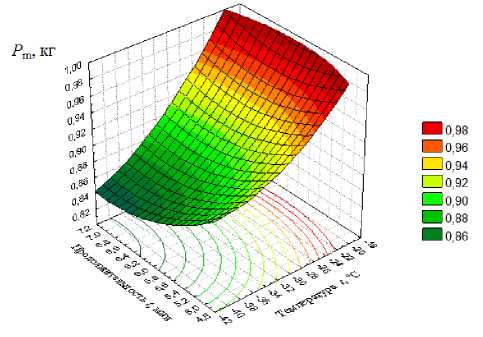
Рисунок 3 – Поверхность отклика и линии равных уровней потерь массы дыни в зависимости от

температуры и скорости замораживания.

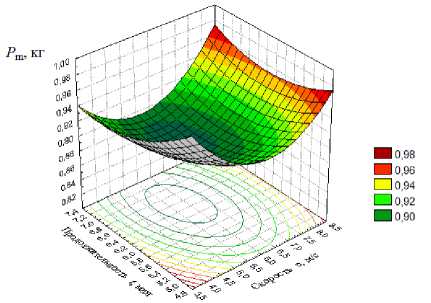
а)

температуры и продолжительности замораживания.

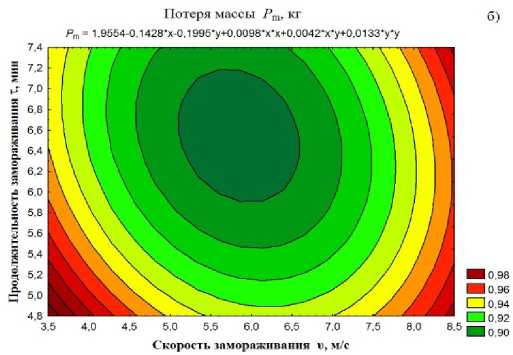
б)

Рисунок 4 – Поверхность отклика и линии равных уровней потерь массы дыни в зависимости от скорости и продолжительности замораживания.

при t = –30oC υ = 5,85 м/с; τ = 6,5 мин;

P m = 0,875 кг;

при t = –35oC υ = 5,66 м/с; τ = 6,8 мин;

P m = 0,843 кг, при которых разница в потере массы дыни составляет 0,032 кг.

Заключение, выводы

Таким образом, принимая во внимание выявленные взаимосвязи между выходными показателями процесса замораживания дыни и полученное оптимальное решение, приходим к следующим рекомендуемым пара-

метрам: – температура замораживания t = от – 30oC до –35oC; – скорость замораживания υ = 5,7 – 5,8 м/с; – продолжительность замораживания τ = 6,5 – 7,0 мин. При этих параметрах замораживания величина потерь массы дыни Pm снижается до 0,843 – 0,875 кг.

СПИСОК ЛИТЕРАТУРЫ 1.    Еренова Б.Е. Научные основы производства продуктов на основе дыни: дис.… докт. техн. наук: 05.18.01. – Алматы, 2010. – 389с. 2.    Грубы Я. Производство замороженных продуктов. – М.: Агропромиздат, 1990. – 335 с. 3.    Алексеев Е.Л., Пахомов В.Ф. Моделирование и оптимизация технологических процессов в пищевой промышленности. – М.: Агро-промиздат, 1987. – 272 с.