Regularity results and solution semigroups for retarded functional differential equations

We consider the following retarded functional differential ecpiation in a. complex Banach space X.

d u dt

( t )— Au ( t ) + A 1 u ( t — r ) + I a ( s ) A 2 u ( t + s ) ds + f ( t ) , 0 < t < T, ^ ^.^

( u (0) — ф 0 , u ( s ) — ф 1( s ) a . e . s E ( —r, 0) .

We assume that A is a densely defined closed linear operator which generates an analytic semigroup) e^{t A} ,t >  0. in X. Sup) pose 0 E p ( A ) for simplicity. A 1 at id A 2 are closed linear operators in X such that D ( A 1) D D ( A ) , D ( A 2) D D ( A ). at id a is a, complex valued

function defined in the interval [ —r, 0] such that a E L 1 ( —r, 0; C).

The following theorems which are improvements of the results by G. Di A. Lorenzi [1] are established in A. Favini and H. Tanabe [2]:

Blasio and

(0.2)

(0.3)

Theorem A Suppose 0 <6 < 1 /p. If the following assumption is satisfied: (I) фо E (X,D(A))6+1 -1 /p,p, ф1 E W(—r, 0; D(A)), f E W(0,T; X). then, there exists a unique solution u of (0.1) satisfying u E W6,p(0, T; D(A)) П C([0, T]; (X, D(A))6+1 -1 /p,p), du/dt E W6'p (0,T; X).

Theorem В Suppose 1 /p <6 <  1. If the following assumption is satisfied:

(W

/

фо E D(A), ф 1 E W6,p(—r 0; D(A)),  ф 1(0) — Фо, f e W6p(0,T; X) n C([0, T]; (X, D(A))6-1 /„),

AФ0 + A1 ф 1(—r) + J a(s) A2ф 1(s)ds E (X,D ( A))6-1 /p,p, then, problem (1.1) admits a unique solution u such that u G W6'p(0,T; D(A)),

(0.4)

(0.5)

du/dt G W⁶ ’ ^p (0 ,T ; X ) П C ([0 ,T ]; ( X, D ( A )) ₆- 1 /p ) .

Note that since A ₂ ф 1 G C ([ —r, 0]; X ), the integral J - a ( s ) A ₂ ф 1 ( s ) ds is well defined.

In this paper we prove further regularity of solutions u when ф 1 and f satisfy more regularity assumptions. Using this result we prove some results on solution semigroups analogous to the one of G. Di Blasio, K. Kunisch and E. Sinestrari [3] when 6 < 1 /p. and to the one of E. Sinestrari [4] when 6 > 1 /p. In case 6 < 1 /p it is shown that the map ^ ф0 ^ ^ ^ u^) ^, where u is the solution of (0.1) with f (t) = 0 and ut(s) = u(t + s), —r < s < 0, is a C0-semigroup in (X, D(A))6+1 - 1 /p,p x W6,p(—r, 0; D(A)), and the characterization of its infinitesimal generater is given. This is nothing but a simple extention of a result of [3] in case where X is a Hilbert space and 6 = 1, p = 2. However, in case 6 > 1 /p the situation is a little more complicated. This is caused by the following fact. In this case there appears the space (X,D(A))6+1 - 1 /p,p which is a subset of D(A). If u belongs to this space. Aiu, i = 1, 2, is defined, lout may not belong to (X,D(A))6- 1 /p,p. Therefore we assume the additional condition AiA-1 G L((X,D(A))6- 1 /p,p), i = 1, 2. A comment on this assumption will be given in section 6. Under these hypotheses it will be shown that the map ф 1 ^ ut Co-semigroup   in   W6,p(—r, 0; D(A)) П C([—r, 0]; (X, D(A))6+1 -1 /p,p)   with characterization of its infinitesimal generater, where again u is the solution of with f (t) = 0 arid ut(s) = u(t + s), —r < s < 0.

For a, Banach space Y we use the following norm of W ^6,p (0 , T ; Y ):

N 6,p,Y, (0 ,T ) ( u )= (^0 ^ \\u ( t ) — u ( s ) ^ Y ( t — s ) ^{- 1 - 6p} dsdt )    ,

HuH w ^6,p (0 ,T ; Y ) = N 6,p,Y, (0 ,T ) ^{( u} ) + ^T -⁶ \^u\ lp (0 ,T ; Y ) •

is а. the (0.1)

(0.6)

1.    Regularity of Solutions: Case 9 < 1 /p

First consider the case 0 <6 <  1 /p. Assume that:

' ф 1 g W ^{1+ 6},^p ( —r, 0; D ( A )) ,   ф о = ф 1 (0) ( G D ( A )) ,

(И)

f G W ¹⁺(0 , T ; X ) П C ([0 , T ]; ( X, D ( A )) 6 +1 - 1 /p,p ) ,

AT 0 + A 1 ф 1 ^{( — r} )+ / a ⁽ s ) ^A 2 ф 1 ⁽ s ) ds ^{G (} X ^{,D (} A )) 6 +1 - 1 /p,p .

-r

Theorem 1. Suppose 0 <6 < 1 /p. Then, under assumption (1-1) the solution of problem (0.1) satisfies u g W1+6,p(0,T; D(A)) П W2+6,p(0,T; X) Fl C 1([0,T]; (X, D(A))6+1-1 /pp)•      (Tl)

Since (1-1) is stronger than (I), in view of Theorem A a solution u of (0.1) exists and satisfies (0.2) and (0.3). Set фо = AФо + A1 ф 1(—r) + j a(s)A2ф 1(s)ds + f(0) •

(1.2)

Then (1-1) implies

Ф о E ( X,D ( A )) ₈ +i - 1 /p,p , ф 1 E W ^6p ( —r, 0; D ( A )) , f ' E W ^6p (0 ,T ; X ) .

Namely, (I) is satisfied by ф о , ф 1 , f ' instead of ф о , Ф ₁ , f. Therefore there exists a unique solution v of the following problem:

v' ( t ) = Av ( t ) + A 1 v ( t

-

r ) + /

-r

a ( s ) A ₂ v ( t + s ) ds + f ' ( t ) ,

0 < t < T,

(L3)

v (0) = ф 0 ,   v ( s ) = ф 1 ( s ) a . e . s E ( —r, 0)

{ v E W ",^p (0 ,T ; D ( A )) П C ([0 ,T ];( X,D ( A )) » +1 - 1 / „) , ( dv/dt E W^6p (0 ,T ; X ) .

Set w ( t ) = ф о + f t v ( т ) dT. Then in A'iew of (1.4)

Г w ' E W ⁶,^p (0 ,T ; D ( A )) П C ([0 ,T ]; ( X,D ( A )) 6 +1 - 1 /pp ) , ( w '' e W ⁶,^p (0 ,T ; X ) .

Since ф о E D ( A ) , v E W ^6p (0 ,T ; D ( A )) C U p (0 ,T ; D ( A )). one lias

w ( • ) = Ф о +

L

v ( T ) dT E C ([0 ,T ]; D ( A )) C U p (0 ,T ; D ( A )) .

(1.4)

(1.5)

(1.6)

In view of (1.5) w ' E W ^6p (0 ,T ; D ( A )) C U p (0 ,T ; D ( A )). By virtue of tins and (1.6)

w E W ¹ ’^p (0 ,T ; D ( A )) C W ⁶’^p (0 ,T ; D ( A )) .                    (1.7)

It follows from (1.7) and (1.5) that w e W1+6’p (0, T; D(A)) П W2+6’p (0, T; X).

Since D(A) C (X, D(A))6+1 -1 /p,p, one has w E C([0,T]; D(A)) C C([0,T]; (X,D(A))6+1 -1 /p,p).

From this and (1.5) it follows w E C 1([0,T];(X,D(A))6+1 -1 /p,p).                        (1.8)

We are going to show

w ( t )= u ( t ) , 0 < t < T.                              (1.9)

If this is proved, then (1.1) follows from (1.7) and (1.8).

Set v ( t ) = ^ Фф-) ) ^<<< <’ 0 Then, v E W ^6p ( —r,T ; D ( A )). Problem (1.3) is transformed to the following integral ecpiation:

v(t) = е*Афо + [ e(t s)AA1 v(s — r)ds + / e(t s)A / a(а)A2v(s + а)dads о                                о            -r

+     e ^{( t - s} ) A f ' ( s ) ds.                                                                    (1.10)

This implies

[ v ( т ) dT = [ e^т A ф ₀ dT + [ [ e ^{( T}-s ) A A 1 v ( s — r ) dsdT 0                 0                   0   0

+ / / e ^{( T}-s ) A[ a ( a ) A 2 v ( s + a ) dadsdT + / [ e ^{( T - s} ) A f ‘ ( s ) dsdT. (1.11) 00      -r                00

• (i)    Case T < r. In view of the definition (1.2) of ф 0 ^one observes

[t e ^TA p 0 dT = [ e ^tA - IA ¹ Ф ,

= ^Ф 0 ^— Ф 0 + ^[ e A ^— I ^] A ¹ ( A 1 Ф 1( ^{— r} ) + У a ^{( s} ) A 2 Ф 1( ^s ) ^ds + ^f (°) ) . (1.12)

With the aid of a. change of the order of integration and an integration by parts

/ / e ^{( т} s ) A A 1 v ( s — r ) dsdT = / / e ^{( T s} ) A A 1 ф 1 ( s — r ) dsdT 00             00

= [ [ e ^{( t - s} ) A — I ] A ^{- 1} A 1 ф 1 ( s — r ) ds 0

= — [ e ^tA — I ] A ^{- 1} A 1 ф 1 ( —r ) + У e ^{( t - s} ) A A 1 ф 1 ( s — r ) ds.

(1.13)

Again changing the order of integration and integrating by parts one obtains

[t Г e(T-s)A /0 a(a)A2v(s + a)dadsdT = Г Г e(T-s)A /0 a(a)A2v(s + a)dadTds 0 0             -r                                    0 s-r t0          tt

= / a(a) e(T-s)AdTA2v(s + a)dads = / / a(a)[e(t-s)A — I]A-1A2v(s + a)dads 0 -r      s0

₌     ^t _{[ e} ( t-s ) A

— I ] A - ¹ /

-

s a (a) A 2 ф1( s + a) dads

r

+ Г [ e ^{( t - s} ) A 0

where

I 1 = У [ e ( t s ) A — I ] A 1 У a ( a ) A 2 ф 1 ( s + a ) dads, I2 = У [ e ( t - s ) A — I ] A - 1 У a ( a ) A 2 v ( s + a ) dads.

Changing the order of integration and integrating by parts yield

I₁ = У a ( a ) У [ e ^{( 1 1} ) A — I ] A ¹ A ₂ ф 1 ( s + a ) dsda

+ / a ( a ) / [ e ^{( 1 - 1} ) A — I ] A ^{- 1} A ₂ ф 1 ( s + a ) dsda 1

=у a ^{( a} ) { - [ e ^tA

-

I ] A ¹ A 2 ф 1 ( a ) + У e ^{( 1 1} ) A A 2 ф 1 ( s + a ) ds j> da

+y ₁ a ^{( a} ) u + A ( a ) {

e ⁽ t + a ) A

-σ

-

I ] A ^{- 1} A 2 ф 1 (0) — [ e ^1A — I ] A ^{- 1} A 2 ф 1 ( a )} da

e ^{( 1 1} ) A a 2 ф 1 ( s + a ) ds j- da

-

/ a ( a )[ e ^1A — I ] A ¹ A 2 ф 1 ( a ) da + -r

_-r a ( a ) ₀ e ^{( 1 1} ) A a 2 ф ₁( s + a ) dsda

+ [ a ( a )[ e ^{( 1 + a} ) A — I ] A ^{- 1} A 2 ф 1 (0) da + [ a ( a ) [

-1                                               -1

-

σ

e ^{( 1 - 1} ) A a 2 ф 1 ( s + a ) dsda.

The sum of the second and fourth terms of the last side of the above equalities is equal to

/¹ _e ( 1-1 ) A / ¹ _a

Jo        J-r

=г e ⁽ -¹ ) A/. ,.

(a) A2 ф 1( s + a) dads + У e(1 1) A У s a (a) A 2 ф 1( s + a) dads.

t

s a (a) A 2 ф 1( s + a) dads

Therefore

I 1 = — У a ( a )[ e ^1A — I ] A ^{- 1} A 2 ф 1 ( a ) da + У a ( a )[ e ^{( 1 + a} ) A

— I ] A ^{- 1} A 2 ф 1 (0) da

⁺ e ^{( 1 - 1} ) A L

s a (a) A 2 Ф 1( s + a) dads.

(1.15)

r

We can show without difficulty

I₂ = У a ( a ) У [ e ^{( 1 1} ) A — I ] A ¹ A ₂ v ( s + a ) dsda

= [ * a ( a ) Г [ e ^{( 1 -} 1 ) A

-t       -σ

— I] A 1-^~ [   A2v (т) dTdsda ds

= [ * a ( a ) Г e ^{( 1 - 1} ) A Г + " A 2 v ( т ) dTdsda -1       -a        Vo

= / a ( a ) / e ^{( 1 - 1} ) A A 2 -t       -σ

= У a ( a ) У e ^{( 1 - 1} ) A A 2

^ф ₀ + У    v ( т ) dT^ dsda — j a ( a

^ф ₀ + У    v ( т ) dT^ dsda

) У e ^{( 1 1} ) A A ₂ ф о dsda

+ У a ( a )[ I — e ^{( 1 + a} ) A ] A ¹ A ₂ ф ₀ da.

(1.16)

From (1.14) - (1.16) and ф ₀ = ф ₁(0) it follows that

[ [ e ^{( T - s} ) A [ a ( a ) A 2 v(s + a ) dadsdr = I 1 + I₂ 0 0             -r

— / a ( a )[ e tA — I ] A ¹ A 2 ф i ( a ) da +

-r

L * e ^{1 t-s )} A L

s a (a) A 2 ф 1( s + a) dads

— I ] A ¹ У a ( a ) A ₂ v ( s + a ) dads = I 1 + I₂ ,

(1.14)

+ £ a ( а ) - e ' t-s • a A 2 ( ф о + f ’ v ( т ) dr) dsda.

(1.17)

As is easily seen

[  [ e ^{( T - s} ) A f ‘ (s ) dsdr = [  [ e ^{( T - s} ) A drf ‘ (s ) ds = [ [ e ^{( t - s} ) A - I ] A ^{- 1} f ‘ (s ) ds

0   0                               0    s                               0

-

[ e ^tA - I ] A ^{- 1} f (0) + j0 t e ^{( t - s} ) A f ( s ) ds.

(1.18)

From (1.11) - (1.13), (1.17), (1.18) the following equality follows easily:

w ( t ) = e ^tA ф 0 + j e ⁽ t ^s ) A A 1 ф 1 ( s — r

) ds + / t e ( t - s ) A J

s

a ( a ) A ₂ dads

+ - a ( a )£ e <  t

^s ) A A ₂ w ( s + a ) dsda + ^ e ⁽ t ^s ) A f ( s ) ds.

(1.19)

.    ( w(t)   0 < t < T, bet w(t) = < А            „ then 1.19 is rewritten as

( ф ₁( t ) —r < t <  0 .

w ( t ) = e ^tA ф 0 + / e ⁽ t ^s ) A A ₁ w( s — r ) ds + / e ⁽ t ^s ) A / a ( a ) A ₂ fu( s + a ) dads 0                                 0             -r

+     e ^{( t - s} ) A f ( s ) ds.

Consequently (1.9) is obtained.

• (ii)    Case r < T <  2 r. By virtue of the result estalohshed in the previous case 0 < T < r we already know that w ( t ) = u ( t ) for 0 < t < r. Hence

w ( t ) = ф 0 + v ( т ) dr + v ( т ) dr = w ( r ) + v ( т ) dr = u ( r ) + v ( т ) dr. 0 r                              r                             r

Since

Au(r) + A1 u(0) + - a(s) A2u(r + s)ds = U(r) — f (r) G (X, D(A))e+1 -1 /p,p, the following facts hold:

' u ,0 ,r ] G W ¹⁺ ”,^p (0 ,r ; D ( A )) ,

_ f G W ¹⁺ »,^p ( r, T ; X ) П C ([ r,T ]; ( X, D ( A )) , +1 - 1 /p,p ) ,

^Au [0 ,r ] ^{( r} ) + A 1 ^u [0 ,r ] ⁽⁰⁾ + j a ^{( s} ) A 2 ^u [0 ,r ] ^{( r} + ^s ) ^{ds G ( X,D (} A )) 9 +1 - 1 /p,p .

Hence (1-1) is satisfied with [ — r, 0], ф 1 replaced by [0 , r ], u [ ₀ ,_r ] respectively. Therefore, by the method of the previous case we can show w ( t ) = u ( t ) for r <  t <  T.

We can proceed to show (1.9) in the general case, and the proof of Theorem 1 is complete.

In case 1 /p <6 <  1 we assume

(П-1)

/

Ф 1 G W ^{1+ 6}’^p ( — r, 0; D ( A )) ( = ^ ф 1 (0) G D ( A )) , f G W ^{1+ 6}’^p (0 ,T ; X ) П C ¹ [0 ,T ]; ( X,D ( A )) 6- 1 /p,p ) ,

^А ф 1 ⁽⁰⁾ + ^A 1 ф 1 ^{( — r ) +} У a ⁽ s ) ^A 2 ф 1 ⁽ s ) ^{ds G ( X,D ( A} )) 6- 1 /p,p ,

^А ф ‘ 1 ⁽⁰⁾ + ^A 1 ф ‘ 1 ^{( — r} ) + У a ⁽ s ) ^A 2 ф ‘ 1 ^{( s} ) ^{ds G ( X,D ( A} )) 6- 1 /p,p , ф ‘ 1 (0)(= D - ф 1 (0)) = Аф 1 (0) + A 1 ф 1 ( — r ) + f ⁰r a ( а ) A 2 ф 1 ( а ) da + f (0) .

Theorem

(0.1) satisfies

2. Suppose 1 /p < 6 <  1. If assumption (II-l) i.s satisfied, the solution u of

u g W ^{1+ 6,p} (0 ,T ; D ( A )) П W ^{2+ 6,p} (0 ,T ; X ) П C ²([0 ,T ];( X,D ( A )) 6- 1 /p,p ) •      (1.20)

If hypothesis (II-l) holds, then (II) is satisfied by ф1 and f ‘ in pl ace of ф 1 and f respectively. Therefore according to Theorem В there exists a unique solution v of the following problem d v dt

( t ) = Av ( t ) + A 1 v ( t — r ) + j a ( s ) A ₂ v ( t + s ) ds + f ‘ ( t ) ,

(1.21)

v ( s ) = ф 1 ( s ) , — r <  s <  0

(1.22)

satisfying v G W6'p (0,T; D (A)), dv/dt G W6,p(0, T; X) П C([0, T]; (X, D(A))6-1 /p).

(1.23)

(1.24)

Set

w ( t ) = ф о + У v ( т ) dT.

(1.25)

In view of (1.23), (1.24) one has w‘ G W6'p (0,T; D (A)),

(1.26)

(1.27)

w ^M G W ^6,p (0 , T ; X ) П C ([0 ,T ]; ( X,D ( A )) 6- 1 /p,p ) .

Since 6 > 1 /p. W 6'p (0 ,T; D (A)) C C ([0 ,T ]; D (A)). He nee v G C ([0 ,T ]; D (A)). From tins and фо G D(A) it followvs that w G C 1([0,T]; D(A)). Tins implies w G W1 ’p(0,T; D(A)) C W6,p(0, T; D(A)). Hence with the aid of (1.26), (1.27) we deduce w g wi+6,p (o, t. d( a)) n w2+e,P (0, t. x).

(1.28)

Since D (A) С (X,D (A)) g- 1 /p,p, one al so has w E C 1([0 ,T ]; (X,D (A)) g- 1 /p,p). From this and (1.27) it follows that w E C2([0, T];(X, D(A))g-1/p,p).

(1.29)

If it is shown that w ( t ) = u ( t ) , 0 < t < T , then in view of (1.28) and (1.29) the proof of Theorem 2 is complete. This part of the proof is almost the same as that of Theorem 1, and so it is omitted.

2.    Solution Semigroup: Case 9 < 1 /p

Suppose assumption (I) is satisfied. Set

Z = ( X, D ( A )) g +i - 1 /p,p x W ^g,p ( —r, 0; D ( A )) .

Following G. Di Blasio, K. Kunisch and E. Sinestrari [3] the solution semigroup for (0.1) is defined as follows:

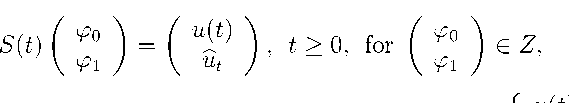
S (t >( £)=( ■t ’P>0 •for Go) e Z where и is the solution of problem (0.1) with f (t) = 0. aiid и

-r < t <  0

и _t ( s ) = b( t + s ) fc>r —r < s <  0. Siiice и E W ^g,p (0 , to ; D ( A )) П C ([0 , to ); ( X,D ( A )) _{g +1} - 1 /_p,_p ), where и E W ^g,p (0 , to ; D ( A )) means и E W ^g,p (0 , T ; D ( A )) for any 0 < T <  to. и ( t ) E ( X-D ( A )) _{g +1} - 1 /_p,_p fc>r t >  0. b E W ^g,p ( —r, to ; D ( A )). and hence и _t E W ^g,p ( —r, 0; D ( A )) for 0 < t <  to. Thei‘efore S ( t ) : Z ^ Z and S (0) = I. It can be shown without difficulty that S ( t ) is a C o-semigroup in Z.

Theorem 3. The infinitesimal generater of the solution semigroup S ( t ) is given by

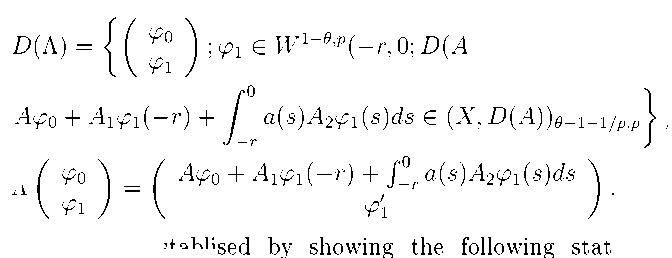
; ф i e W ^{1+ g,p} ( —r, 0; D ( A )) , ф i (0) = ф o ,

^A ф o + ^A 1 ф 1 ^{( — r} )+ / a ⁽ s ) ^A 2 ф 1 ⁽ s ) ds ^{E ( X,D (} A )) g +i - 1 /p,p

Л ( ф o ) = ( Aф o + A i ф i ( —r ) + J' ⁰ _r a ( s ) A 2 ф i ( s ) ds _{φ 1                                 φ} ′ ₁

This theorem can be establised by showing the following statements following G. Di Blasio, K. Kunisch and E. Sinestrari [3]:

• (1)    S ( t ) D (Л) С D (Л) ,

(h) D (Л) is deiise in Z,

(hi) Л С iiffiiiitesinial generator of {S ( t ) },

(iv) Л : D (Л) С Z ^ Z is closed .

Problem (0.1) is rewritten as

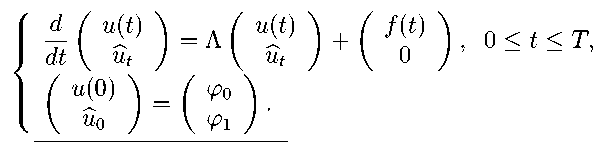
^“ 1 t ))=л( “(t )) + ( ^f ( t > T 0 < t < T dt    “ t              “ t           0 у

“(0) A = ( фo u0          φ1

(2.2)

The mild solution of (2.2) is expressed as

(t t ⁾) = s - 1 ) ( ф 0 ) + £ * s - 1 - s ) ( f о ) ) ds.

Ч Ф 0) ^e solution, and

D (Л) arid f e C ¹([0 ,T ];( X,D ( A )) 6 +1 - 1 _/p,_p ). then

(ub\ ¹)

is a strict

u e C 1([0,T];(X,D(A))6+1 - 1 /p,p), b e C 1([0, T]; W6,p(-r, 0; D(A))),                                              (2.3)

d ( U ’ ) = S - 1 )Л ( ^{ф 0} ) + S ( t ) ( ^f 0 ⁰⁾ ) + / * S - 1 - s ) ( ^f ' 0 s ) ) ds.

Starting from u e C([0,T]; Lp(-r, 0; D(A))) ^ u e Lp(-r,T; D(A))

one can show that (2.3) is equivalent to b e W ^{1+ 6,p} ( -r/T ; D ( A )). Thus the following assertion holds:

Theorem 4. If the following assumptions are satisfied:

ф 1 e W ^{1+ 6},^p ( -r, 0; D ( A )) ,   ф о = ф 1 (0) ,   f e C 1 ([0 ,T ]; ( X, D ( A )) 6 +1 - 1 /p,p ) ,

Aф0 + A1 ф 1(-r) + J-r a(s)A2ф 1(s)ds e (X,D(A))6+1 -1 /p,p, then a solution of (0.1) satisfying u e W1+6,p(0,T; D(A)) П C 1([0,T]; (X, D(A))6+1 -1 /p,p)

exists and is unique.

3.    Regularity of Solutions: Case 0 > 1 /p

In this section we suppose that the following assumptions are satisfied:

(11-2)    A 1 A ^{- 1} , A 2 A ^{- 1} e L(( X,D ( A )) 6- 1 /p,p , ( X,D ( A )) 6- 1 /p,p )■

(п-3) I

ф 1 e W ⁶,^p ( -r, 0; D ( A )) П C ([ -r, 0]; ( X,D ( A )) 6 +1 - 1 /p,p ) , f e W ⁶,^p (0 ,T ; X ) n C ([0 ,T ]; ( X, D ( A )) 6- 1 /p,p ) .

Remark 1. Set ф ₀ = ф 1 (0). Then it follows from (II-3) that ф ₀ e ( X,D ( A )) _{6 +1 -} 1 /_p,_p. Hence Aф ₀ e ( X,D ( A )) _6- 1 /_p,_p. Frот ф 1 e C ([ -r, 0]; ( X,D ( A )) _{6 +1 -} 1 /_p,_p ) it follows that

^A Ф 1 ^e C ^([ -r, ^0] ; ^{( X,D (} A )) 6- 1 /p,p ) ,   j a ⁽ s ) ^A ф 1 ⁽ s ) ds ^{e ( X,D (} A )) 6- 1 /p-p ■

Hence by (H-2)

A 1 ф 1 ^e C ^([ -r, ^0] ; ^{( X,D (} A )) 6- 1 /p,p ) ,   j a ⁽ s ) A 2 ф 1 ⁽ s ) ^d s ^{e ( X,D (} A )) 6- 1 /p,p .     (3.1)

Hence the final condition of (II) is satisfied. Therefore (H-2) and (H-3) imply (II).

Remark 2. (H-2) is equivalent to

A i e L(( X, D ( A ))₆ +1 - 1 /p,p , ( X, D ( A )) e- 1 /p,p ) , i = 1 , 2 .

A comment on assumption (H-2) will be given in the final section.

Theorem 5. Suppose 9 >  1 /p, and assumptions (II-2) and (II-3) are satisfied. Then the solution u of problem (0.1) satisfies

u e W p (0 , T ; D ( A )) П C ([0 , T ]; ( X, D ( A )) e +1 _ 1 ,„, ) , di/» e W ^ep (0 ,T ; X ) П C ([0 ,T ]; ( X, D ( A )) ,— 1 /p „) .

(3.2)

(3.3)

Suppose first T < r. Let u ₀ be the function defined by

t uo(t)= etA[ф 1 (0) + A-1 f(0)] + уо e(t-s)Af.(s)ds — A-1 f(0),

(3.4)

where

f ( s ) = A 1 ф 1 ( s — r ) + f ( s )+ / a ( a ) A 2 ф 1 ( a ) da,

e ^{( s} ) = f ^{( s} ) ^— ,e⁽⁰⁾ = ^A 1 ф 1 ^{( s — r} ) + ^{f ( s} ) ^{— A} 1 ф 1 ^{( — r} ) ^{— f (0)} .

It follows from (11-3) and (3.1) that

f e W ^e,p (0 ,T ; X ) П C ([0 ,T ];( X,D ( A )) e- 1 /p,p ) , f e W⁶/ (0 ,T ; X ) П C ([0 ,T ]; ( X,D ( A )) e- 1 /pp ) , ^ф 0 + ^{A f (0) e ( X,D ( A} )) 6 +1 - 1 /p,p .

(3.5)

(3.6)

(3.7)

The solution of (0.1) is obtained as the solution of the following integral ecpiation

u ( t )= u ₀( t ) + j e ⁽ t ^s ) A j a ( a )[ A ₂b( s + a ) — A ₂ ф 1 ( a )] dads,

(3.8)

where b( s ) = ^ ф ^) S ^ 0’ This equation is sovled by successive approximation:

u n +1 ( t )= u o ( t ) + 0 e ⁽ ts ) A - a ( a )[ A 2 b _n ( s + a ) — A 2 ф 1 ( a )] dads, n = 1 , 2 , 3 ,.... (3.9)

It is shown in A. Favini and H. Tanabe [2] that u _n e W ^6,p (0 ,T ; D ( A )) , u _n (0) = ф ₀ , n = 0 , 1 , 2 ,... . From (3.9) it follows that

U n + 1 ( t )

-

u n ( t ) = J e ⁽ t s ) A J a ( a )[ A 2 b n ( s + a ) —

A 2 u n

1 ( s + a )] dads.      (3.10)

If —r < a < —T. then s + a < t — T <  0. Hence

A 2 u n ( s + a ) — A 2 u n- 1 ( s + a ) = ф 1 ( s + a ) — ф 1 ( s + a ) = 0 .

Therefore (3.10) is rewritten as

U n + 1 ( t )

-

u n

( t ) = f J 0

e ( t-s ) A

I a ( a )[ A 2 b n (

s + a ) — A ₂ b n- 1 ( s + a )] dads.

(3.11)

It is proved in [2] that

11 ^u n +1 ^— u n\\w 6,p (0 ,T ; D ( A)) < C 2 k 2 l l a l L 1( -T, 0) [^{( 9p} )   1 /p C 0 ⁺ 1 ] ll u n ^— u n- 11| W 9.P (0 ,T ; D ( A ))

for some constants C 0 , C 2 indeperident of T and k ₂ = Ц A ₂ A ¹||. There fore if T is so small that

C 2 k 2H 1 ( - t, 0) [ ( Op ) - ^{1 /p} C 0 + 1 ] <  1 ,                      (3.12)

then

∞

^2 Hu n +1 ^— u n ^ W ®’^p (0 ,T ; D ( A )) < ^.                        (3.13)

n =1

Set

W⁸/ (0 ,T ; X ) = {u G W p (0 ,T ; X ); u (0) = 0 }•

The following lemma is due to G. Di Blasio [5] (Theorem 10 if 9 <  1 /p and Theorem 8 if 9 >  1 /p ). Also c.f. Lemma 1 of G. Di Blasio and A. Lorenzi [1].

Lemma 1. Suppose 9 = 1 /p. If x G (X,D(A))8+1 - 1 /p,p, then e-Ax g Wp(0,T; D(A)) П C([0,T]; (X, D(A))6+1 -1 /pp)•

The following lemma is Theorem 24 of G. Di Blasio [5].

Lemma 2. Suppose 9 >  1 /p. Then, if f G W^p (0 , T ; X ), the funotion V ( t ) = jt e ⁽ t-s ) A f ( s ) ds _say_to^_es

V G W8’p (0,T; D (A)), dV/dt = AV + f G C([0, T]; (X, D(A))8-1 /pp),              (3.14)

and the following inequality holds with a constant C 2 independent of T;

ll ^V I I W ⁶

(0 ,T ; D ( A )) < C 2 || ^f I I W ^в» (0 ,T ; X ) •                              (3.15)

In A. Favini and H. Tanabe [2] it is shown that the constant C 2 above can be chosen Independent of T If we choose (0.6) as the norm of W^8,p (0 , T ; D ( A )).

Let V and f be as in Lemma 2. With the aid of (3.14) and (3.15) one observes

^{| V} I I w ⁶

(0 ,T ; X ) = ll ^{AV + f} I I w ⁶-P (0 ,T ; X ) ^{A | V} I I w ⁶-p (0 ,T ; D ( A )) ⁺ ll ^f I I w ⁶-p (0 ,T ; X )

• < ⁽ C 2 ⁺ 1)|| ^f || w 6,p (0 ,t _; x ) •                                                                (3.16)

From Lemma 2 the following lemma follows:

Lemma 3. Suppose 9 >  1 /p. Let f G W ^’p (0 ,T ; X ) П C ([0 ,T ];( X,D ( A )) 8 - 1 /p,p ). Then, for V ( t ) = jt e ^{( t-s} ) A f ( s ) ds otic has

V G W^8,p (0 ,T ; D ( A )) n C ([0 ,T ]; ( X,D ( A )) 8 +1 - 1 /p,p ) •

In view of Lemma 1, 3 and (3.6), (3.7) one observes e-'AIФ 1(0) + A-1 f (0)] e C([0,T];(X,D(A)),+1 -, ,„),

J , e - ^{( -} ‘ ⁾ A S . ( s ) ds e C ([0 , T ]; ( X, D ( A )) , +1 _ 1 /„„ ) .

Moreover. A-1 f (0) is a, constant function with a, value in (X, D(A))6+1 _1 /p,p. Consequently u0 e C([0,T];(X,D(A))6+1_1 /pp).

(3.17)

(3.18)

Suppose for some n = 1 , 2 ,...

U n e C ([0 ,T ];( X,D ( A )) 9 +1 - 1 /pp ) •

Then u n e C ([ —r,T ];( X,D ( A )) 6 +1 - 1 /p,p ). He nee A ₂ b n e C ([ —r,T ];( X,D ( A )) 6- 1 /pp ) In view of Remark 2. Therefore it is easy to show

⁰ a ( a )[ A 2 u n ( ■ + a ) - A 2 ф Д a )] da e C ([0 ,T ]; ( X, D ( A )) 6- 1 /pp ) •       (3.19)

Since U n e W ⁶’^p (0 ,T ; D ( A )). one lias b n e W ^6p ( —r,T ; D ( A )). and lienee A 2 U n e W ^6,p ( —r,T ; X ) The following lemma is proved in A. Favini and H. Tanabe [2, Lemma 2.5]:

Lemma 4. Suppose v e W ⁶p ( —r,T ; X ), 0 <9 <  1 , 9 = 1 /p. Hlen f^O r _r a ( a ) v ( ■ + a ) da e W⁶,^p (0 ,T ; X ) . and

/ a ( a ) v ( ■ + a ) da

-r

W ⁶

(0 ,T ; X )

< ^a^ L 1( -r, 0) [ ^ 6,p, ( -r,T ) ^{( v )+ T 6} Hv^ L p ( -r,T ; X )] •

Applying Lemma 4 to A ₂b _n one observes f ° a ( a ) A ₂ b n ( ■ + a ) da e W ^6,p (0 ,T ; X ). Therefore, noting (3.1) one deduces

I a ( a )[ A 2 b_n ( ■ + a ) - A 2 ф 1 ( a )] da

= [ a ( a ) A 2 b n ( ■ + a ) da — / a ( a ) A 2 ф 1 ( a ) da e W ^’p (0 , T ; X ) •

(3.20)

-r-r

By virtue of (3.19), (3.20) and Lemma 3 one obtains

e ⁽ -^-s ) A 1° a ( a )[ A 2 b n ( s + a ) —

A 2 ф 1 ( a )] dads e C ([0 ,T ]; ( X,D ( A )) 6 +1 - 1 /p,p ) •

(3.21)

From (3.9), (3.17) and (3.21) it follows that (3.18) holds with n + 1 in pl ace of n. Next, we estimate the following norm:

I| h ^Z ^ L ^p (0 ,T ;( X’D ( A )) 6,p ) = (|| V ‘ W L p (0 ,_T . _x ) +       |H ‘ ⁽ t ) | 6,p ^dt )      ,

(3.22)

where | ■ l ₆,_p is the semi norm defined by

^{| u |} 6,p =

¹ -⁶ A^Au

\\^pt - ¹ dt)

i /p

The following inequality was shown in the proof of Lemma 2 of G. Di Blasio [5]:

||^V ‘^ L p (0 ,T ; X ) <  (( ^p - 1) ^{/6p )(} p ¹ /p M 1 ^{T 6} N 6,p, (0 ,T ) ⁽ f )+ M 0 Il f || lp (0 ,T ; X ) ,        (3.23)

where M ₀. M 1 are constants such that || e^M|| < M ₀ , | |( d/dt ) e^M\| < M 1 (t. In the proof of Theorem 26 of [5, p. 81] it was shown that

/^T |V ‘ ( t ) ¹

^p,p di <  2⁴ p- ² M ^{2 p} ( 6 ^{- p}

+ (1

- ⁶ ) —p ) ^w ) ( f ) + ( Op ) - ¹ JT t ^{- 6p} If ( t ) B p dt)

T∞

+2 ^{p - 1} M p      t ^{- 6p} \f ( t ) \ ^p dt     ( s + 1)

-

- ps - ^{1+ p - p6} ds.

(3.24)

It is easy to show the following inequality holds for f E W ^p (0 , T ; X ) with a constant c independent of T:

/ r ^6p ||f ( t ) I p dt < cfl/1 , ., (0 ,TX ) ■                         (3.25)

From (3.22) - (3.24) and (3.25) it follows that the following inequality holds with a constant

C 1 indepeiident of T:

j ^T |V ‘ ( t ( I g di < C 1 If I , ., (0 TX ) ■                      (3.26)

By virtue of (3.22), (3.23) and (3.26) the following inequality holds for f E W ®^,p (0 , T ; X )

with a, constant C ₂ indepeiident of T:

II V ‘ H b p (0 , T ;( X, D ( A )) ep ) <  ^C 2^{( T 6 +} 1) Il f ((' ⁹ p (0 , T ; X ) ■                     (3.2 < )

The following lemma is also due to Lemma 11 of G. di Blasio [5].

Lemma 5. Suppose 6 > p. Then

W6-p(0, T; X) П Lp(0, T; (X, D(A))„) C C([0, T]; (X, D(A))6-1 /,,,), and the following inequality holds for u E W6,p(0, T; X) П Lp(0, T;(X,D(A))6,p) with a constant C3 indepeiident of T:

HuH c ([0 ,T ];( X,D ( A )) e- 1 /pp ) <  ^C 3 ( ^{T 6 1} /p lul rn ⁹p (0 ,T ; X ) ^{+ T} 1 /p ^u^ L p (0 ,T ;( X,D ( A )) e,p ) ) ■   (3.28)

Inequality (3.28) follows from the one in case T = 1 and considering a function u ( Tt ) , 0 < t <  1. in the general case.

In view of Lemma 5

I I V ‘ \ c ([0 ,T ];( X,D ( A )) e- 1 /p ,p ) <

(3.29)

< ^C 3 ( ^{T 6 - 1 /p} \V ‘ \ , ^e,p (0 ,T ; X ) ⁺ T — ^{1 /p} \ ^V ‘ \ L ^p (0 ,T ;( X,D ( A )) e,p ) ) ■

Inequalities (3.16), (3.27) and (3.29) yield

(3.30)

II V'Нс([0,T];(X,D(A))6- 1 /p,p) < CT \f IIWe,p(0,T;X), where Ct = Cз ((C2 + C2 + 1)T6 + C2) T-1 /p. Hence

^HV 11 с ([0 ,T ];( X,D ( A )) 6 ₊₁ - 1 /p,p ) = || ^AV li e ([0 ,T ];( X,D ( A )) ₆— 1 _Mp )

= ^HV ' ^{- f} 11 с ([0 ,T ];( X,D ( A )) 6- 1 /p,p ) < C T У ^H W 6,p (0 ,T ; X ) ⁺ Il f || c ([0 ,T ];( X,D ( A )) 6- 1 /p,p ) • (3.31)

We apply (3.31) to J ⁰ _T a ( a )[ A ₂b n ( • + a ) — A ₂b _n- 1 ( • + a )] da. Then V = u n ₊₁ — u n (c.f.

(3.11)). Let T satisfy (3.12):

C 2 k 2 Hl i ( -t, 0) [( Op ) ^{- 1 /p} C 0 + 1] <  1 •

One has

^Hu n +1 ^— u n|| c ([0 ,T ];( X,D ( A )) 6 +1 - 1 /p,p )

≤ C T

+

I a ( a )[ A 2 b n ( • + a ) —

A 2 b n- 1 ( • + a )] da

I a ( a )[ A 2 b „ ( • + a ) — A 2 b n_ 1 ( • + a )] da

W ⁶,p (0 ,T ; X )

.

(3.32)

с ([0 ,Т ];( X,D ( A )) 6- 1 /p,p )

It is shown in [2] that the following inequality holds:

I a ( a )[ A 2 b n ( • + a ) —

A 2 u b n- 1 ( • + a )] da

< k 2 HaH L 1 ( -T, 0) [( 9p ) ^{- 1 /p} C 0 + 1] Hb n

-

W ⁶ p (0 ,T ; X ) u n- 1 I I W ^6,p (0 ,T ; D ( A )) •

(3.33)

As is easily seen

I a ( a )[ A 2 b n ( • + a ) —

A 2 u b n- 1 ( • + a )] da

c ([0 ,T ];( X,D ( A )) 6- 1 /p,p )

sup sG [0 ,T]

/  a ( a )[ A 2 b n ( s + a ) — A 2 b n- 1 ( s + a )] da

-T

( X,D ( A )) 6- 1 /p,p

• <[  |a ^{( a} ) |d ^a sup   ||^A 2 b n ^{( T} ) ^— A 2 b n - 1 ^{( T} ) ^H ( X,D ( A )) 6- 1 /pp

  -T           T G [ -T,T ]

• < ^k 2 || a^H L 1 ( -T, 0) ^su P ^HAu n ^{( T} ) ^{— A} u n- 1 ^{( T} ) ^H ( X,D ( A )) 6- 1 /pp

t G [0 ,T ]

= ^k 2 || a^H L 1 ( -T, 0) || u n ^— u n- 1 ||c ([0 ,T ];( X,D ( A )) 6 +1 - 1 /p,p ) •

(3.34)

The following inequality follows from (3.32) - (3.34):

^Hu n +1 ^{— u} n|| c ([0 ,T ];( X,D ( A )) 6 +1 - 1 /p,p ) < C T k 2 HaH L 1 ( -T, 0) [( 9p ) - ^{1 /P} C 0 + 1] Hb n

-

u n- 1|| w ^6,p (0 ,T ; D ( A ))

^{+ k} 2 || a^H L 1 ( -T, 0) ll u n ^— u n- 1 || c ([0 ,T ];( X,D ( A )) 6 +1 - 1 /p,p ) •

Summing both sides from n = 1 tо m one gets

m

52 u n +1 - u n \\ c ([0 ,T ];( X,D ( A )) 9 +1 _ 1 /p,p ) n =1

m

• <    C T k 2 \а\ _£ 1 ( -т, 0) [⁽ 9p ) ¹ /p C 0 + 1 ] 52 ^Wu n ^— u n- 1 ^W ^ ⁹'^p (0 ,T ; D ( a ))

n =1

m

+ k 2|| a|| _L 1 ( -T, 0) 52 ^W u n ^— u n- 1 \ c ([0 ,T ];( x,d ( a )) 9 +1 - 1 /p,p ) •                    ^-^

n =1

Substituting

m

52 ^Wu n ^— u n- 1 \ c ([0 T ];( X,D ( A )) 9 +1 - 1 /p,p ) n =1

m

• <    52 ^Wu n +1 ^— u n ^W C ([0 T ];( X,D ( A )) 9 +1 - 1 /p,p ) ^{+ W}u 1 ^— u 0 ^W C ([0 ,T ];( X,D ( A )) 9 +1 - 1 /p,p ) n =1

in the last side of (3.35) one gets

m

52 ^Wu n +1 ^— u n W c ([0 ,T ];( X,D ( A )) 9 +1 - 1 /p,p ) n =1

m

• <    C T k 2 Ца^ ь 1 ( -T, 0) [ ( ep) - ^{1 /p} C 0 +1] 5^1 u n ^— u n- 1 U rn ⁹-p (0 ,T ; D ( A ))

n =1

m

+ k 2 || ^a|| _L i ( - t, 0) 52 ^Wu n +1 ^— u n- W c ([0 T ];( X,D ( A )) 9 +1 - 1 /p,p )

n =1

+ k 2 || ^{а Ц} L 1 ( - t, 0) || u 1 ^— u 0 ^W C ([0 ,T ];( X,D ( A )) 9 +1 - 1 /p,p ) •

This implies

m

(^{1 —} k 2|| a|| _L 1 ( -T, 0)) 52 ^Wu n +1 ^— u n ^W C ([0 T ];( X,D ( A )) 9 +1 - 1 /p,p ) n =1

m

• <    C T k 2 || ^{а Ц} L 1 ( -T, 0) [ ( ep ) ^{- 1 /p} C ; +1] 52 w u n ^— u n- 1 \ m ⁹-p (0 ,T ; D ( A ))

n =1

+ k 2 ^Ца^Ц ь 1 ( -T, 0) ^Wu 1 ^— u 0 \ c ([0 ,T ];( X,D ( A )) 9 +1 - 1 /p,p ) •                              (3.36)

Letting m ^ to in (3.36) one obtains in view of (3.13)

∞

(^{1 —} k 2 ^Ца^Ц ь 1 ( -T, 0)) 52 ^Wu n +1 ^— u n \ c ([0 ,T ];( X,D ( A )) 9 +1 - 1 /p,p ) n =1

∞

• <    C T k 2 ^ца^ц ь 1 ( -T, 0) [ ( ep) - ^{1 /p} C 0 +1] £ Uu n ^— u n- 1 ^W m ⁹-p (0 ,T ; D ( A ))

n =1

+ k 2|| a|| _L 1 ( -T, 0) ^Wu 1 ^— u 0|| c ([0 ,T ];( X,D ( a )) 9 +1 - 1 /p,p ) < №•                       (3.37)

Let T satisfy k ₂|| а |Д i ( _-T, ₀ ) <  1 besides T < r and (3.12). Then by virtue of (3.37) and (3.13) one obtains

∞

^2 u n +1 - u n ^ C ([0 ,T ];( X,D ( A )) ₆ +i _ i ^p ) < TO.

n =1

Hence {u n } is convergent in C ([0 ,T ]; ( X,D ( A )) _{6 +1} _ 1 /_p,_p ). Si nee u n ^ u in W ^6,p (0 , T ; D ( A )). one concludes u G C ([0 , T ]; ( X,D ( A )) _{6 +1} _ 1 /p,p ) and

U n ^ u in W ^6,p (0 ,T ; D ( A )) О C ([0 ,T ];( X,D ( A )) 6 +1 - 1 /pp ) .

Let T ₀ satisfy

0 < T 0 < r, C 2 k 2 |a| _L 1 ( -T 0 , 0) [( Op ) ^{- 1 /p} C 0 + 1] <  1 , k 2 |a| _L i ( - t 0 , 0) <  1 .

Then, by the result just proved one has u G    W ^6,p (0 , T ; D ( A )) О

C([0,T0]; (X, D(A))6+1 -1 /p,p)'. Hence b G w6,p(-r, T; D(A)) О C([-r, TД (X, D(A))6+1 -1 /pp).

Suppose T) < T. Then bl[t0-r,T0] G W6,p(TD - r,T0; D(A)) О C([T0 - r,T0]; (X,D(A))6+1 -1 /pp), and u satisfies d u dt

( t ) = Au ( t ) + A 1 u ( t - r ) + j a ( s ) A ₂ u ( t + s ) ds + f ( t ) , T 0 < t < T,

u ( S ) = b | [ t 0 -r,T 0 ] ( s ) , T 0 - r < s < T 0 .

Therefore, by virtue of the result already proved u G W6,p(0,T; D(A)) О C([0, min{2T0,T}]; (X,D(A))6+1 -1 /p,p).

Continuing this process we can complete the proof of Theorem 5.

Next, we consider the case where the following assumption is satisfied:

Г ф 1 g W ^{1+ 6},^p ( -r, 0; D ( A )) О C 1 ([ -r, 0]; ( X,D ( A )) 6 +1 - 1 /p,p ) ,

(11-4) j f G W ^{6 +1} ’^p (0 ,T ; X ) О C ([0 ,T ]; ( X,D ( A )) 6 +1 - 1 /p,p ) О C 1 ([0 ,T ]; ( X,D ( A )) 6- 1 /p,p ) , [ Ф 1 (0) = Aф 1 (0) + A 1 ф 1 ( -r ) + J^-* ³ r a ( а ) A 2 ф 1 ( а ) da + f (0) .

Theorem 6. If assumptions (II-2) and (II-4) are satisfied, then the solution u of (0.1) satisfies u g W1+6,p(0,T; D(A)) О W2+6’p(0,T; X) О C 1([0,T]; (X,D(A))6+1 -1 /p,p), u" G C([0,T];(X,D(A))6-1 /p).

(3.38)

Proof. If hypotheses (H-2) and (П-4) are satisfied, then (H-l) and (H-3) are also satisfied. In view of Theorem 2 and Theorem 5 it suffices to show u‘ G C([0,T];(X,D(A))6+1 -1 /p).

Since (II-4) is satisfied, (II-3) is satisfied by ф1, f ‘ in pl ace of ф 1, f. Therefore in view of Theorem 5 there exists a solution v of the following problem d v dt

( t ) = Av ( t ) + A 1 v ( t — r ) + j a ( s ) A 2 v ( t + s ) ds + f' ( t ) ,

v ( s ) = Ф 1 ( s ) , —r < s <  0 satisfying

v E W ^6p (0 ,T ; D ( A )) П C ([0 ,T ]; ( X,D ( A )) e +i - 1 /pp ) , dv/dt E W (0 ,T ; X ) П C ([0 ,T ]; ( X, D ( A )) e- 1 /p ) .

Since u ( t ) = ф ₁(0) + У v ( т ) dт (c.f. Proof of Theorem 2).

u ‘ = v E C ([0 ,T ];( X, D ( A )) e +i - 1 /pp ) .

□

4. Solution Semigroup: Case 0 > 1 /p

In this section we assume that hypotheses (II-2) and (П-3) are satisfied. Let Z = W ^6p ( —r, 0; D ( A )) П C ([ —r, 0]; ( X, D ( A )) e ₊i - 1 /p,p ) .

For ф ₁ E Z let u be the solution of (0.1) with f ( t ) = 0:

d u dt

( t ) = Au ( t ) + A 1 u ( t — r ) + j a ( s ) A 2 u ( t + s ) ds, 0 < t < ro,

(4Л)

u ( s ) = ф ₁( s ) , —r < s <  0 .

In view of Theorem 5 u satisfies

u e W »'^p (0 ,T ; D ( A )) П C ([0 , T ]; ( X, D ( A )) e +1 - 1 /p,p ) , u ‘ e W ^6,p (0 , T ; X ) П C ([0 , T ]; ( X, D ( A )) e- 1 /p,p ) .

Therefore b E W ^6,p ( —r, ro ; D ( A )) П C ([ —r, ro ); ( X,D ( A )) _{6 +1 - 1} /_p,_p ). wlrere u E W ^e'^p ( —r, ro ; D ( A )) means u E W ^6p ( —r,T ; D ( A )) VT >  0. Tins implies b t E Z for t >  0. Therefore if we set

S ( t ) ф 1 = b t , t >  0 ,

S ( t ) nirips Z to Z.

Let b lie the solution of (4.1). v lie the solution of (4.1) with the initial function bT and w(t) = b(t + т) fc>r т > 0, t > 0. Then d v dt

( t )= Av ( t ) + A ₁ v ( t — r ) + У a ( s ) v ( t + s ) ds, 0 < t< ro,

v(s) = b(т + s), —r < s < 0, dd           0

—w ( t ) = n- u ( t + т ) = Au( t + т ) + A ₁ u ( t + т — r ) +     a ( s ) u ( t + т + s ) ds

^dt            ^dt                                                                   r

= Aw ( t ) + A ₁ w ( t — r ) + У a ( s ) w ( t + s ) ds, 0 < t < ro,

w ( s ) = b( т + s ) , —r < s <  0 .

Therefore v = w. arid lienee vt = wt. On the other hand vt = S (t) bт = S (t) S (т) ф i, wt (s) = w (t + s) = b( t + s + т) = bt+т (s) = (S (t + т) ф i)( s).

Thus

S ( t ) S ( т ) ф i = S ( t + т ) ф i .

It is easy to see that the mapping [0 ,T ] Э t ^ b _t E C ([ —r, 0]; ( X,D ( A )) _{e +1} - ₁ /p,p ) is continuous. The continuity of [0 , T ] Э t ^ b _t E W ^e,p ( —r, 0; D ( A )) is shown in the following lemma.

Lemma 6. For v E W^e,p ( —r,T ; D ( A )) the mapping [0 , T ] Э t ^ v_t E W^e,p ( —r, 0; D ( A )) is continuous.

Proof. The lemma is proved by the following step:

• (i)    For w E W ^{1 ,p} ( —r,T ; D ( A )) lim _T^t I w - w t ^ w «.p ( -r, 0; D ( a )) = 0.

• (ii)    For v E W ^ep ( —r,T ; D ( A )), w E W ^{1 ,p} ( —r,T ; D ( A )) such that || v — w| _w e.p ( _-r,_{T ;} D ( A )) < e one has

^{| v} T ^— v t ^ w ⁹.p ( -r, 0; D ( A ))

• <    ^{| w} T ^— w t I I w ⁹.p ( -r, 0; D ( A )) ^{+ | v} T ^{— w} T I I w e.p ( -r, 0; D ( A )) ⁺ || ^v t ^{— w} t||w ^9,p ( -r, 0; D ( A ))

• <    ^{| w} T ^{— w} t I I w ⁹.p ( -r, 0; D ( A )) +2 || v ^{— w |} w «.p ( -r,T ; D ( A )) < ^{| w} T ^— w t ^ w e.p ( -r, 0; D ( A )) ^{+ 2 e} .

□ Hence the mapping [0 , T ] Э t ^ S ( t ) ф ₁ = b _t E Z is continuous. Thus it has been shown that {S ( t ) , t >  0 } is a, C o-seriiigroup.

The following result is an analog to Theorem 4.4 of E. Sinestrari [4]:

Theorem 7. The infinitesimal generator of S ( t ) is given by

D (Л) = { ф 1 E W ^{1+ e},^p ( —r, 0; D ( A )) П C ¹ ([ —r, 0]; ( X, D ( A )) e +1 - 1 /p,p );

I a ( a ) A 2 ф 1 ( a ) da } ,

ф1(0) = Aф 1(0) + A1 ф 1(—r) + л ф 1 = ф1 .

Proof. We show

• (i)    S ( t ) D (Л) c D (Л).

• (ii)    D (Л) is deiise in Z = W ^e,p ( —r, 0; D ( A )) И C ([ —r, 0]; ( X, D ( A )) e +1 - 1 /p,p )•

(hi) Л c iiihriitesiriial generator of {S ( t ) }.

(iv) Л : D (Л) c W ^e’^p ( —r, 0; D ( A )) ^ W ^e'^p ( —r, 0; D ( A )) is closed.

• (i)    Let ф ₁ E D (Л) and b be the solution of (4.1). Then in view of Theorem 6 arid Its proof b (0) = ф ₁(0) ar id b ‘ (0) = ф 1 (0). He rice b E W ^{1+ e,p} ( —r, ж ; D ( A )) И C ¹([ —r, ж ]; ( X,D ( A )) e +1 - 1 /p,p )• Hence

b t e W ^{1+ e,p} ( —r, 0; D ( A )) И C ¹([ —r, 0]; ( X,D ( A )) e +1 - 1 /p,p ) .

For t >  0

(b t ) ‘ (0) = lim u t f s ) s→ 0

-

s

ub t (0)          ub ( t + s ) — ub ( t )          u ( t + s ) — u ( t )

----= lim ------------ = lim ------------ s→- 0        s           s→- 0        s

= U ( t ) = Au ( t ) + A 1 b( t — r ) + / a ( s ) A 2 b( t + s ) ds

-r

= Au t (0) + A 1 b t ( —r ) + / a ( s ) A 2 b t ( s ) ds.

-r

Hence b _t E D (A).

(ii) Let ф 1 E Z and

b _t = S ( t ) ф 1. Set ф _е = 0 b _t dt. ф _е ( s ) = 0 b _t ( s ) dt = 0 b(t + s ) dt.

Therefore

Hence

V e ⁽ s )

= d           (s) = ddbt + s)dt =/'b‘(t + s)dt ds 0               ds 0                 0

= b( € + s ) — b( s ) = b(€ + s ) — ф 1 ( s ) = b _e ( s ) — ф 1 ( s ) , —r < s <  0 .     (4.2)

ф _£ = b _E — ф 1 E W ^6,p ( —r, 0; D ( A )) П C ([ —r, 0]; ( X, D ( A )) 6 +1 - 1 /p,p ) .

Ф , E W ⁶+1 -p ( —r, 0; D ( A )) П C 1 ([ —r, 0]; ( X, D ( A )) 6 +1 - 1 / „) .

By virtue of (4.2)

Aф _€ (0) + A 1 ф _£ ( —r ) + - a ( а ) A 2 ф _€ ( а ) da

= A Г b(t ) dt + A 1 Г b( t — r ) dt + Г a ( а ) A 2 Г b( t + а ) dtda 0                 0                   -r 0

= j ^A b( t ) + A 1 b(t — r ) + j a ( а ) A 2 b(t + а ) da^ dt

= ( b‘ ( t ) dt = b( € ) — b(0) = b _£ (0) — ф 1 (0) = ф _Е (0) .

Therefore ф _£ E D (A). Since [0 , то ) Э t — u _t E Z is continuous,

e

∥ ϵ ^{- 1} φ ϵ -

ф 1 ^ z = ¹ [^£ ( b1 ^€ Jo

t

-

e

ф 1 ) ^dt     < € I I

Ut — ф i I z dt —— 0 as € —— 0 .

Z

• (iii)    Let ф 1 E D (Л) and u be the solution to (4.1). As was noted in the proof of (i) one has b E W ^{1+ 6,p} ( —r, то ; D ( A )) П C ¹ ([ —r, то ]; ( X, D ( A )) _{6 +1 -} 1 /_p,_p ). Hence

b ‘ E W ⁶-^p ( —r, то ; D ( A )) П C ([ —r, то ]; ( X, D ( A )) 6 +1 - 1 /„.,, ) .

Therefore j b (ta + •) da — b

< [ \\b ⁽ t^a + • ) 1⁰

j b' ( ta + • ) da

W ^e,p ( -r, 0; D ( A ))

= j (b ' ( ta + • ) — b ) d

^— b ' ^ W 9,p ( -r, 0; D ( A )) ^da ^ ⁰ ,

-u

σ

W ^e-p ( -r, 0; D ( A ))

< L

Hence

lib ' ^{( ta} + • ) ^—

C ([ -r, 0];( X,D ( A )) _{6 +1} _ 1 _{M p} )

^b ' I C ([ -r, 0];( X,D ( A )) ₆ +i _ i /_p

) ^da ^ ⁰ •

S ( t ) ф 1 — ф 1 = b t

-

t

b0 b( t + • ) — b( • )    1 Г¹ д

~ = —t— = 1 /0 dau ^{( ta +} • ’ ^da

= j b' ( ta + • ) da ^ b ' ( • ) = Л ф 1

in Z.

(in) Let ф 1 n

G D (Л) , ф 1 n ^ ф 1 , ф 1 n = Л ф 1 n ^ Д in Z. Then ф 1 = Д G Z. Hence ф 1 G W ¹⁺ »^p ( —r, 0; D ( A )) П C ¹ ([ —r, 0]; ( X, D ( A )) , +1 - 1 / „) .

Since ф 1 _n

^ ф 1 iii C ([ —r, 0]; ( X, D ( A )) ₆ +1 _ 1 _/p,_p ). one lias Аф 1 n (0)   ^ Aф 1(0).

Аф 1 n(—r) ^ Аф 1(—r)• J-r a(a)A2ф 1 n(a)da ^ -rr a(a)A2ф 1 (a)da ii 1 (X, D(A))e-1 /p,p. One also has ф n(0) ^ Д(0) = ф1(0) in (X,D(A))6+1 - 1 /pp Therefore, from ф1 n (0) = Aф 1 n(0) + A1 ф 1 n(—r) + I a(a)A2ф 1 n(a)da it follows that

ф 1⁽⁰⁾ = ^A Ф 1⁽⁰⁾ + ^A 1

ф 1( —r )+ /

-r

a ( a ) A ₂ ф 1( a ) da.

Therefore ф 1 G D (Л) and Л ф 1 = Д.

□

5.    Remark on Hypothesis (П-2)

Let A be the realization in U * (O) , 1 < p <  to, of a strongly elliptic linear partial differential operator of second order with the Dirichlet boundary condition, where О is a bounded domain in R n. Let A i ,i = 1 , 2 , be linear partial differential operators of second order in О Assume that tlre coefficients of A,A i ,i = 1 , 2 , and the boundary д О of О are sufficiently smooth. Then D ( A ) = W ^{2 ,p} (О) П W 0^{1 ,p} (O). Assume that A has a bounded inverse. Suppose 1 /p < 6 <  3 / (2 p ). Then 0 <  2 6 — 2 /p <  1 /p . Hence by virtue of the results of R. Seeley [6] (also c.f. H. Triebel [7, Theorem 4.3.3]).

( L ^p (O) , D ( A )) _e- 1 /p,p = ( L ^p (O) , W ² ’^p (О) П W 1 ^,p (O)) ₈- 1 /p,p = = Bp^ ^{2 /p} (O) = W ^{2 8 - 2 /p},^p (O) •

(5.1)

Since

A-1 G L(Lp(Q), W2,p(Q) П W01 ,p(Q)) П L(W1 ’p(Q), W3’p(Q) Fl W01 ,p(Q)), one has

A - ¹ G L (W ^{2 6}- ^{2 /p}’^p (Q) , W ^{2+2 6}- ^{2 /p}’^p (Q) П W 0^{1 ,p} (Q)) .                (5.2)

Let f G ( L ^p (Q) ,D ( A )) 6- 1 /p,p . In view of (5.1) and (5.2) A - ¹ f G W ^{2+2 6}- ^{2 /p}’^p (Q) F l W 0 ¹ ’^p (Q). Hence

AA - ¹ f G W ^{2 6}- ^{2 /p}’^p (Q) = ( L ^p (Q) , D ( A )) 6- 1 /pp , i = 1 , 2 .

Therefore

AA ^{- 1} G L(( L ^p (Q) , D ( A )) 6- 1 /pp , ( L ^p (Q) ,D ( A )) 6- 1 /p,p ) , i = 1 , 2 .         (5.3)

Next, consider the case of the Neumann boundary condition. In this case

D(A) = {u G W2'p(Q); du/dn = 0 on dQ} , where du/dn is the outer conormal derivative with respect to A. Suppose 1 /p < 9 < 3/(2p) + 1 /2, 9 = 1 /2+ 1 /p. Then, again by virtue of the results of R. Seeley [6] or H. Triebel [7]

(L (Q) ,D (A)) e-1 /„, = B2^-1 /p) (Q) = W2(6-1 /p),p (Q), and (5.3) follows as in the case of the Dirichlet boundary condition.