Рекомендации по самостоятельному изучению темы «Aксиомы отделимости топологических пространств»

Социально-экономическое развитие нашей страны обуславливает коренное совершенствование высшего образования. Повышается значимость подготовки кадров, создаются условия для переподготовки специалистов высшего образования на уровне международных стандартов.

Исходя из естественных требований общественной жизни и экономики, одной из основных задач модернизации системы высшего образования является внедрение в обучение современных форм и технологий на основе изучения международного опыта.

Указ Президента Республики Узбекистан «О мерах по дальнейшему совершенствованию сферы информационных технологий и коммуникаций» от 19 февраля 2018 года и постановление Кабинета Министров Республики Узбекистан «О мерах по коренному совершенствованию и повышению эффективности системы подготовки кадров в Ташкентском университете информационных технологий имени Мухаммада ал-Хоразмий» от 24 июля 2018 года предусматривают коренное совершенствование и повышение эффективности подготовки кадров в этом вузе, а также его филиалах. Важный шаг в осуществляемой системе новшеств — внедрение с 2018-2019 учебного года кредитной системы обучения для подготовки кадров в сфере информационных технологий и коммуникаций с целью обеспечения вхождения университета в число самых престижных вузов мира.

Понятие топологического пространства является весьма общим. Поэтому невозможно доказать многих интересных свойств обо всех топологических пространств сразу. В связи с чем вводят специальные классы топологических пространств. Очевидно, что чем уже рассматриваемый класс, тем большим количеством интересных свойств обладает этот класс.

Цель написания статьи – научить студентов мыслить самостоятельно и работать над собой. Следующая статья также станет отличным руководством для самостоятельной организации занятий.

Краткое содержание статьи выглядит следующим образом: Изложим аксиомы отделимости – наборы дополнительных требований, налагаемых на топологические пространства, касающиеся разделения точек и замкнутых множеств в топологических пространств и позволяющие изучать ограниченные классы топологических пространств.

Наиболее широко используемыми аксиомами отделимости являются: T ₀, T ₁, T ₂ , T ₃, T , T ₄.

Пусть ( X , т ) некоторое топологическое пространство.

T (аксиома Колмогорова).  Говорят, что пространство X удовлетворяет aксиоме T , если для любых двух различных точек x и y пространства X по крайней мере одна из них имеет окрестность, не содержащую вторую точку.

Антидискретное пространство является примером пространства, не являющего Т _о - пространства. Приведем другой пример.

Пример 1. Пусть X = {0,1,2,3,4}. Семейство т = {0,{0}, {1}, {2}, {0,1}, {0,2}, {1,2}, {0,1,2} ,{0,1,2,3,4}} является топологией на X.

Задание. Показать, что ( X , т ) не удовлетворяет аксиоме Т _о.

Т 1 ( аксиома Тихонова ). Говорят, что пространство X удовлетворяет аксиоме Т , если для любых двух различных точек x и у пространства X каждая из них имеет окрестность, не содержащую другую точку.

Задание. Доказать, что топологическое пространство является Т - пространством тогда и только тогда, когда его любое одноточечное подмножество замкнуто.

Ясно, что всякое Т -пространство является Т _о -пространством.

Обратное, в общем случае, не верно.

Пример 2. Рассмотрим множество

• X = [0,1]

и семейство на нём

т = { A с X :U A}u{ X}

Задания. Показать, что:

• a )    ^т является топологией на X ;

• b )    пространство ( X , т ) не удовлетворяет аксиоме Т 1 ;

• c )    пространство ( X , т ) удовлетворяет аксиоме Т ₀ .

Т₂ (аксиома Хаусдорфа). Говорят, что пространство X удовлетворяет аксиоме Т , если любые различные точки x и у пространства X имеют непересекающиеся окрестности.

Пространство, удовлетворяющее аксиоме   Т2, называется хаусдорфовым пространством или отделимым пространством.

Ясно, что всякое   Т ₂ -пространство является Т -пространством.

Обратное, в общем случае, не верно.

Пример 3. Рассмотрим множество

X = N = {1,2,..., n,...} и топологию на нём т = { A с X :7 £ A}^{ A с X :| X \ A |<да)}.

Задания. Показать, что:

• a )    пространство ( X , т ) не удовлетворяет аксиоме Т ₂;

• b )    пространство ( X , т ) удовлетворяет аксиоме T .

Задания. Показать, что:

• a )    прямая Зоргенфрея;

• b )    плоскость Немыцкого являются хаусдорфовыми пространствами.

Аксиома T . Говорят, что пространство X удовлетворяет аксиоме Т ₃, если для любого замкнутого множества и не содержащейся в нём точки существуют их непересекающиеся окрестности.

Пространство X удовлетворяет аксиоме T тогда и только тогда, когда для любой точки x и её окрестности U существует окрестность V , такая, что x е V с [ V ] с U .

Пространство, удовлетворяющее аксиомам T и T называется регулярным пространством.

Всякое регулярное пространство является хаусдорфовым. Обратное утверждение, в общем случае, не верно.

Пример 4. Пусть X = (-да, +да) — множество всех действительных чисел. Рассмотрим множество

D =U ± 1, ± 1

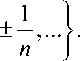
I        2    3

Для каждого x е X определим следующие множества и систему. U i ( x ) = ( x - 1, x + 1) , ii

v ^{( x} ) = {

{ U i (x ): i = 1,2,3,..., n ,... } , x * 0

{ u , ( x )\ D : i = 1,2,3,..., n ,... } , x = 0

Система v = U v ( x )     удовлетворяет условиям     ( NS 1) - ( NS 3)

x е X

.Топологическое пространство X , наделенное топологией, порожденной системой окрестностей v , является хаусдорфовым пространством. Множество D замкнуто в X . Кроме того, 0 £ D . Очевидно, что U n V *0 для любых открытых множеств U и V , таких, что 0 е U и D с V . Следовательно, X не является регулярным пространством.

Аксиома T . Говорят, что пространство X удовлетворяет аксиоме 32

T J ,если для любого замкнутого множества F и не содержащейся в нём 32

произвольной точки x ₀ существует непрерывная функция f : X ^ [ 0,1 ] , такая, что f ( x ₀) = 0 и f ( x ) = 1 для всех x е F .

Пространства, удовлетворяющие аксиомам T и T называются 32

вполне регулярными пространствами или тихоновскими пространствами.

Каждое вполне регулярное пространство регулярно. Обратное утверждение не верно. Контрпример строится довольно сложной техникой. Поэтому его привести не будем.

Запомните! Существует регулярное, но не вполне регулярное пространство, такое, что непрерывными функциями на нем являются только константы.

Аксиома T . Говорят, что пространство X удовлетворяет аксиоме Т ₄, если для любых двух замкнутых в X , непересекающихся множеств существуют их непересекающиеся окрестности.

Пространство X удовлетворяет аксиоме T тогда и только тогда, когда для любого замкнутого множества F и его произвольной окрестности U существует окрестность V , такая, что

F с V c[V ]с U.

Пространство, удовлетворяющее аксиомам T и T называется нормальным пространством .

Каждое нормальное пространство вполне регулярно. Обратное не верно.

Пример 5. Плоскость Немыцкого является вполне регулярным, не являющимся нормальным пространством. Приведем ее е конструкцию.

Рассмотрим замкнутую верхнюю полуплоскость L = { ( x , y ) : у >  0 } и прямую L = { ( x , у ) : у = 0 } . Положим L, = L \ L Для каждого ( s , 0) е L и r >  0 пусть

U (( с , 0), r ) = { ( x , у ): ( x - s ) + ( у + s ) ² <  r ² }

Пусть, далее

U ( s , 0) = U ^ ( s , 0 ) , 1     { ( s , 0 ) } ,             i = 1,2,...

Для каждого ( s , Z ) е L и r >  0 пусть

^U ( ( ^s , ^z ) , ^r ) = { ( x , у ) ^{: (} x - ^{s )2} + ⁽ у + ^{Z )2} <  r ², ^z >  ⁰ } ,

U i ( s , Z ) = и | ( s , Z ) ,1 j ,                     i = 1,2,...

Совокупность

v = {U; (s,Z): (s,Z) е L, i е N} является фундаментальной системой окрестностей в L.

Относительно топологии т ,порожденной этой системы множество L замкнуто в пространстве (L,t ). Более того, всякое F с L замкнуто L . В частности, множества A = {(x,0): x е Q} и B = {(x,0): x е R \ Q} замкнуты L , где Q - множество рациональных чисел. Ясно, что x е V c[V ]с U AAB = 0

Но, для всякой пары открытых в L множеств U и U , содержащих

A и B , соответственно, имеем

U A U B ≠∅ .

Таким образом, L не является нормальным пространством.