Реологическая модель деформационного поведения сахарного теста в условиях одноосного сжатия

Кондитерские массы, подвергающиеся формообразованию (пралиновые конфетные массы, сахарное и затяжное тесто, фруктовоягодные начинки, пасты и пр.) обладают одновременно упругостью, вязкостью, пластичностью и эластичностью. Указанные свойства характеризуются такими реологическими константами как модуль упругости, вязкость, предел текучести.

Знание закономерностей деформационного поведения перерабатываемых кондитерских масс с определенными реологическими свойствами позволяет рассчитать параметры процесса формообразования и подобрать технологическое оборудование для его проведения.

Целью работы является вывод реологического уравнения деформационного поведения сахарного теста в условиях одноосного сжатия, реализуемого в процессах формования заготовок сахарного печенья.

Структурная реологическая модель упруговязко-пластичного тела (рисунок 1), к которому можно отнести сахарное тесто, имеет вид [1]:

UVP — B - K — [ H - ( N i Stv ) ] - ( H 2| N 2 ) , (1) где UVP – упруго-вязко-пластичное тело; B – тело Бингама; K – тело Кельвина.

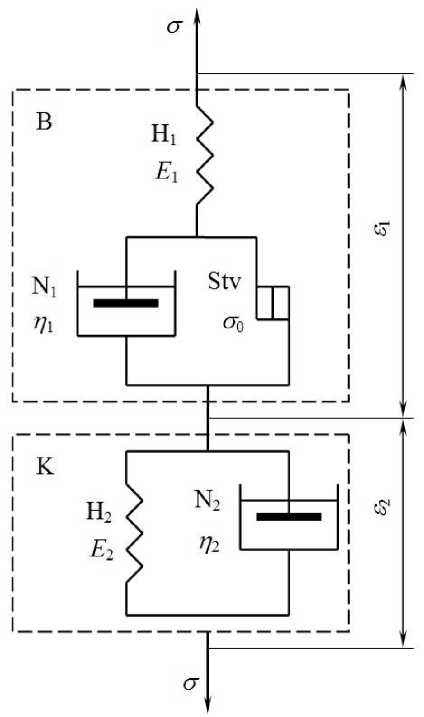
Рисунок 1. Реологическая механическая модель упруго-вязко-пластичного тела

Упруго-вязко-пластичное тело состоит из последовательно соединенных тел Бингама B и Кельвина K (рисунок 1). Тело Бингама включает в себя элемент Гука H₁ с модулем упругости E 1 , элемент Ньютона N 1 с вязкостью n и элемент Сен-Венана Stv с пределом текучести o ₀. Тело Кельвина K состоит из элемента Гука H 2 с модулем упругости E 2 и элемента Ньютона N 2 с вязкостью n 2 .

На основании принципа суперпозиций Больцмана общая деформация г упруго-вязкопластичного тела равна (рисунок 1):

г = г + г ,            (2)

где г 1 - деформация тела Бингама; г ₂ - деформация тела Кельвина.

Уравнение состояния тела Бингама [1, 2]:

J g   1 do о - со

—1 =--+-----0 ,(3)

dt   Ex dtn где о - нормальное напряжение; t - время.

Уравнение состояния тела Кельвина-Фойгта [3,4]:

d^  E2о

- + — г = dt   П 2

Складывая (3) и (4) с учетом (2), получим:

d e  E.     1 d o  оо

— + — г =--+ — +---°"(5)

dt   п     E dt

Выражая из уравнения (5) деформацию e , получим:

_ 1 n- do  П- o ^2 o - oo

O^ —          +      +

E E₂ dt  E₂ n   E₂   П

Дифференцируя (6) по t , имеем:

^{d s} - ₌ П -   dО ! 1 d o , П - d o  n - d^2e ^

dt EvE2 dt- E2 dt E2n dt  E2dt

Подставляя г из уравнения (6) и de, dt

из (7) в уравнение (4), после преобразований получим реологическое уравнение состояния упруго-вязко-пластичного тела:

d ^- о  ( E,  E,  E ,) d o   E.E_? о - о

+    +   +       + dt    (П 2   П1   П 2 ) dt    П - П1

_ d ^- £ EE d s

= E 1 ^ +— dt      П2

Реологическое уравнение (8) позволяет выполнить имитационное моделирование поведения упруго-вязко-пластичного тела как в квазистатических режимах при постоянных значения деформации или напряжения (испытания на ползучесть или релаксацию напряжений) так и в динамических режимах при изменении напряжения или деформации по гармоническому закону с заданными значениями амплитуды и частоты колебаний.

Рассмотрим поведение упруго-вязкопластичного тела в условиях квазистатическо-го испытания на ползучесть, в ходе которого заданной величиной является напряжение, а измеряемой - относительная деформация.

Пусть в начальный момент времени ( t = 0) к упруго-вязко-пластичному телу приложено внешнее напряжение ст* , которое далее остается постоянным. Причем приложенное напряжение превышает предел текучести, т. е. ст * >  ст ₀. После преобразований уравнение (8) принимает вид неоднородного дифференциального уравнения второго порядка:

dг E, de E

-ГТ + — т = -^- (ст — ст 0)   (9)

dt   n dt  ППг

Решение уравнения (9) складывается из общего решения однородного уравнения и

формирования упруго-вязко-пластичного тела (рисунок 2, кривая 2). Деформация г упр являет-

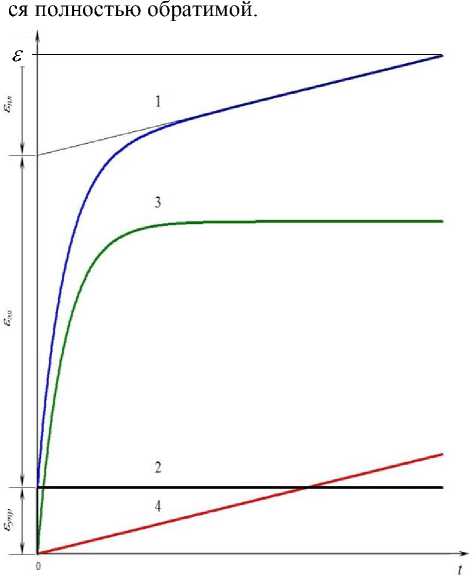
Рисунок 2. Развитие общей (1), упругой (2), эластической (3) и пластической (4)деформаций упруговязко-пластичного тела во времени

частного решения при начальных условиях [5, 6]:

соответствующих

* * ( стст г = — + — 1 — e

- &t )

П 2

E i    E 2

\

* ст + —

—

П 1

ст

— t (10)

Как следует из уравнения (4), в произвольный момент времени t общая деформация г упруго-вязко-пластичного тела (рисунок 2, кривая 1) складывается из трех деформаций -мгновенной упругой г упр (первое слагаемое),

Одновременно с этим начинают деформироваться тела Кельвина K и Бингама B (рисунок 1). Деформация тела Кельвина приводит к возникновению эластической деформации г эл (так же полностью обратимой), которая развивается во времени по экспоненциальному закону и является запаздывающей (рисунок 2, кривая 3), т.к. мгновенному растяжению пружины H₂ препятствует демпфер N₂. При t ^ да эластическая деформация асимптотически стремится к гуковской деформации:

эластической г эл (второе слагаемое) ческой г„ (третье слагаемое).

Из уравнения (9) видно, что каждой деформации, накопленной

и пласти-

величина к произ-

вольному моменту времени t , зависит от рео-

логических

констант

упруго-вязко-

пластичного тела и определяется величиной приложенного напряжения ст* .

В начальный момент времени t = 0 мгновенно деформируется элемент Гука H 1 (рисунок 1), на кривой кинетики деформации (рисунок 2, кривая 1) наблюдается скачкообразное увеличение относительной деформации на величину г упр . Мгновенная упругая деформация развивается в течение долей секунды и остается постоянной в течение всей продолжительности де-

*

_ ст ^г упр ^(да) = ^

Градиент скорости развития эластической деформации убывает по экспоненциальному закону. В начальный момент времени t = 0 градиент скорости имеет максимальное значение:

*

г Эл (0) = —,

П 2

а при t ^ да градиент скорости г ‘_л (да) = 0 .

Одновременно с этим в упруго-вязкопластичном теле развивается пластическая деформация г пл , что является следствием деформирования тела Бингама B (рисунок 1). Пластическая деформация, необратимая по величине, развивается во времени по линейному

закону (рисунок 2, кривая 4). Пластическое

течение протекает с постоянным градиентом скорости развития деформации:

£

*

а

- ^а о

пл

П

В том случае, если приложенное напря-

жение не превышает предел текучести, т. е. ст* < а , то в упруго-вязко-пластичном теле

развиваются только упругая и эластическая деформации без накопления остаточной.

С целью оценки применимости реологического уравнения (10) для описания деформационного поведения образцов сахарного теста был проведен ряд экспериментов. Объектом исследования явилось тесто для приготовления сахарного печенья [7].

Экспериментальные исследования были проведены на реометрическом комплексе собственной конструкции в условиях одноосного сжатия исследуемого цилиндрического образца теста между двумя пластинами. Величина нормального (сжимающего) напряжения составляла (кПа) 1,63; 2,53; 3,8; 5,15 и 6,37.

Выбор искомого диапазона изменения нормального напряжения продиктован необходимостью изучения деформационного поведения теста как в упругой области (до начала пластического течения), так и в той области, где реализуется, собственно, пластическое (необратимое) деформирование теста. При величине нормального напряжения более чем 6,5 кПа наблюдалось «выползание» теста из зазора между пластинами, что, безусловно, искажало полученные результаты.

В условиях одноосного сжатия образца теста при постоянном сжимающем напряжении осуществляли измерение возникающей при этом абсолютной деформации с последующим вычислением относительной деформации. В ходе сжатия фиксировали изменение относительной деформации образца во времени с последующим построением графических зависимостей в координатах деформация-время (рисунок 3).

Общим для всех графических зависимостей является появление мгновенной упругой и эластической деформаций.

Мгновенная упругая деформация г упр обнаруживает себя в момент времени t = 0. Эта деформация присуща твердой фазе дисперсной системы, представленной, в данном случае, клейковинным каркасом. Величина мгновенной упругой деформации характеризуется величиной силы первичных химических связей структуры.

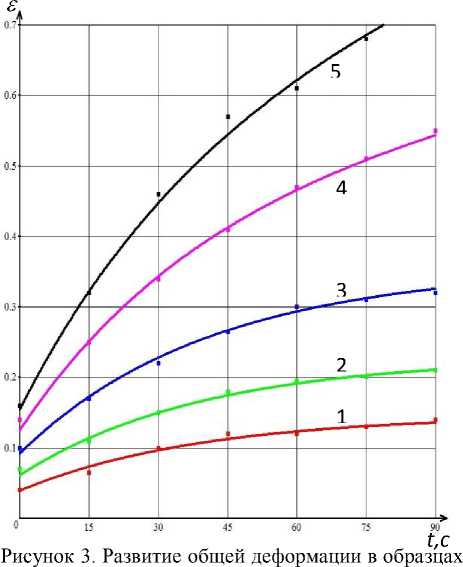
теста при нормальной нагрузке: 1 - 1,63 кПа;

2 - 2,53 кПа; 3 - 3,8 кПа; 4 - 5,15 кПа; 5 - 6,37 кПа

Эластическая составляющая г эл общей деформации является запаздывающей и развивается во времени, стремясь к установившемуся значению. Эластическая деформация характерна для образованной дисперсной фазой пространственной сетки с тонкими прослойками дисперсионной среды. Она является результатом скольжения частиц дисперсной фазы друг относительно друга без разрыва межмолекулярных связей и поэтому не сопровождается разрушением структуры. Эластическая деформация г эл характеризует не только первичные, но и вторичные силы химической связи, действующие между макромолекулами структуры и их звеньями.

Кинетические кривые г = f ( t ) , полученные при сжимающем напряжении 1,63 и 2,53 кПа (рисунок 3, кривая 1, 2) имеют нелинейный вид и не содержат финишного линейного участка, что указывает на отсутствие (в данных условиях) пластической деформации. Дальнейшее увеличение сжимающего напряжения приводит к возникновению в исследуемых образцах теста необратимых пластических деформаций, что выражается в появлении на кривых г = f ( t ) финишных линейных участков (рисунок 3, кривая 3, 4 и 5).

Пластическая деформация г пл представляет собой течение материала с одновременным разрушением и тиксотропным восстановлением структуры. Причем процессы разрушения преобладают над восстановлением, что и приводит к возникновению остаточной деформации после снятия внешнего напряжения.

В процессе пластической деформации происходит изменение ориентации частиц дисперсной фазы, определяемое направлением действия деформирующих систему сил.

Обработка экспериментальных данных (рисунок 3) по известной методике [1, 2, 3], позволила получить значения реологических констант (таблица 1), входящих в уравнение (10). Установлено, что при доверительной вероятности 95 %, реологическое уравнение (10) адекватно описывает экспериментальные данные. Максимальная ошибка при этом составляет 2,3 %.

Т а б л и ц а 1

Реологические свойства теста на пшеничной муки и маргарина

Модуль упругости		Вязкость		Предел текучести σ 0, кПа
быстрой эластической деформации E 1, кПа	медленной эластической деформации E 2, кПа	пластическая η 1, кПа ⋅ с	Упругого последействия η 2, кПа ⋅ с
41,31	15,21	1151,2	600,01	3,68