Решение начально-краевой задачи для колебаний каскадной системы твердых тел на балке Эйлера - Бернулли

Каскадная система твердых тел представляет собой произвольное число твердых тел, скрепленных между собой и балкой упругими связями и расположенных вертикально по отношению к горизонтально расположенной балке. Твердые тела испытывают колебания в вертикальном на- правлении, а балка, которую считаем балкой Эйлера — Бернулли, — из-гибные колебания также в этом направлении. Рассматриваемая механическая система представляет собой упруго распределенную систему в виде балки с бесконечным числом степеней свободы, динамическое поведение которой описывается линейным дифференциальным уравнением в частных производных относительно смещений точек оси балки, и систему с сосредоточенными параметрами в виде твердых тел с конечным числом степеней свободы, динамическое поведение которых описывается системой обыкновенных дифференциальных уравнений относительно линейных смещений твердых тел. Совокупность линейных дифференциальных уравнений в частных производных и системы обыкновенных дифференциальных уравнений, называемая гибридной, выведена с использованием вариационного принципа Гамильтона [1]. При этом точечное взаимодействие балки с прикрепленной системой твердых тел учитывается дельтафункцией Дирака. Этот факт предусматривает применение понятия обобщенного решения гибридной системы дифференциальных уравнений [2, 3, 4, 5], а также применение аппарата обобщенных функций [6, 7]. Под начально-краевой задачей понимается нахождение обобщенного решения гибридной системы дифференциальных уравнений с учетом начальных и краевых условий. Решение начально-краевой задачи в данной работе опирается на результаты исследований соответствующей краевой задачи на собственные частоты и формы колебаний [8]. Отметим, что данная математическая модель в первом приближении может моделировать колебания многоэтажных зданий и сооружений, установленных на основании, которое является в той или иной степени упругим.

Целью настоящей работы является постановка задачи на собственные частоты, вывод условия ортогональности для собственных колебаний и решение начально-краевой задачи. Следует отметить, что при решении начально-краевой задачи существенно используются собственные частоты и соответствующие им формы колебаний.

1 Задача на собственные значения

Рассмотрим гибридную систему дифференциальных уравнений движения изгибных колебаний балки длины l с каскадно закрепленной системой твердых тел [1] (рис. 1).

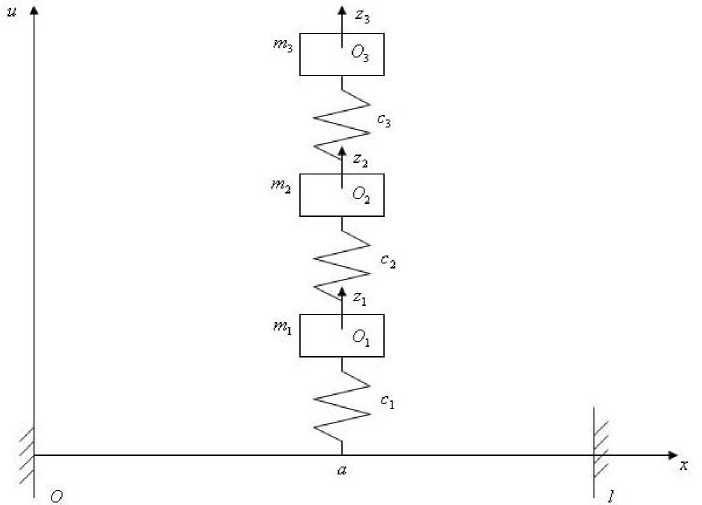
Рис. 1. Пример каскадной системы с тремя твердыми телами ( n = 3 )

• • mh + c

( z 1 - u ( a , t

-

c 2 ( ^z 2

^z 1 ) ^0,

m.z. + c z. - z - c z - z = 0, i i i i i - 1 i + 1 i + 1 i

( i = 2,..., n - 1),

m z + c z - z = 0, n n n n n - 1

d ² u     d ⁴ u

( z 1 - u ( x , t ) ) 5 ( x - a )

pF   + EJ = c dt2      dx4 1

Здесь z i = z i ( t )— смещение i- го твердого тела, u = u ( x , t )— поперечные смещения точек оси балки, x — координата точек оси балки, t — время, m i — масса i- го твердого тела, c i — коэффициент жесткости i- й пружины, р — плотность стержня, F — площадь поперечного сечения балки, E — модуль упругости балки, J — момент инерции сечения балки относительно нейтральной оси, перпендикулярной плоскости колебаний, а — координата точки закрепления твердого тела, 5 ( x - а ) — функция Дирака.

Запишем приближенное решение (1) в виде конечных рядов:

m z. (t) = Е Ф, (t) Ai, i = 1,2,..., n ,                       (2)

i    kk k = 1

m

u ( x , t ) = Е Ф _к ( t)V_k ( x ),                             (3)

k = 1

где Ф к ( t ) — скалярная функция, зависящая от переменной t , Ak

— ам-

плитуда i -го тела в k -й гармонике, V_k ( x ) — амплитуда точки оси балки с координатой x в k -й гармонике.

Подставим (2) и (3) в уравнение (1).

В результате получим

Е ф д t ) m1 A k + Ф k ( t ) [ c1 ( A k - Vk < a ) ) - c ₂ ( A - A k ) ^] = °

Е ф”л t ) m. A k + Ф k ( t ) [ ci ( A k - A k ^{- 1} ) - ci _{+ 1} ( A k ^{+ 1} - A k ) ] = °

m

Е ФЛ t ) m A ⁺ Ф k ( t ) [ cn ( A n - A k ^{- 1} ) ] = °

m                                          m

Е ф'л t ^{) V} k ⁽ x ) + ^{Ьф (} t ) Vkxxxx ⁽ x ) = Е Ф k ⁽ t )e 1 ( A k - Vk ( x ) ) ⁵⁽ x - a ) .

. 1                                                                                                                                 1

Отсюда для каждой к -й гармоники получим уравнения:

Ф k ( t ) m J Ak

+Фk

⁽ t ) _ ^c 1 ( Ak

^- Vk ( a ) ) ^- c 2 ( Ak ^- Ak ) ] = ⁰-

Ф k ⁽ t ) miAk

⁺ Ф k < ' > [ ci ( Ak - Ak - 1 ) -4+ 1 ( Ak + 1 - Ak ) ^] = °,

^Ф k ⁽ t ) mnAk ⁺

^ф k ⁽ t ) ^cn ( An-

— Ak ^{- 1} ) ] = °

Ф К ⁽ t^)Vk ^{( x} ) ^{+ b} Ф _k ⁽ t ) Vkxxxx ^{( x} ) = Ф _k ⁽ t ) ^e1 ( A _k - Vk ^{( x} ) ) ⁵ ( ^x - a ) .

Положим фК,(t) = -^k^k(t).

Подставив в (4) и сократив на ф _к ( t ), получим задачу на собственные частоты ® k :

2 J .

— го₇ т_л A + к 1 к

cl ⁽ Ak Vk ⁽ a ) ) c 2 ⁽ Ak Ak ) _ ⁰

• — гоГО^ m .Al + c. (Al — Al     — c. A л1    — Al j — 0,

k i k L i \ k k ) i + 1 \ k k /_

• — го, ² m An + c An — An П — 0, k n k L n\ k k )

• — го ² V , ( x ) + b V,       ( x ) — e, (A¹ — V , ( x )^ 5 ( x — a ).

k k ' kxxxx '    1 \ k k ' / ^{v 7}

Отметим, что

V k ^{( x} ) ^—

e i V k ( x — a ) A_x 1 + e 1 V k (0) ^k

где V k ( x ) — решение краевой задачи [8]:

277 / X , d 4 V k ( x )         x

—rok Vk (x)+ b —л— — 5(x) dx с краевыми условиями на концах балки, например, для шарнирного опирания:

V k ( — a ) — 0, V ;(— a ) — 0, V k ( l — a ) — 0, V /( l — a ) — 0 .

Подстановка Vk(a) в первые n уравнений в (6) приводит к линейной однородной системе алгебраических уравнений относительно неизвестных амплитуд Ak,Ak,...,Ak. Приравнивая нулю определитель из коэффици ентов при этих амплитудах, получаем частотное уравнение относительно rok.

Рассматривая систему из первых n - 1 уравнений в (6), выражаем, например, A k ,..., A kn через A k :

A k — A k g k , i — 2,3,..., n , где множитель g_ik зависит только от частоты ro _k и параметров механической системы.

X ^y kxxxx , j ) v kxx , jxx ) ^.

Тогда преобразованное последнее уравнение в (6) примет вид:

• -»k(Vk, Vj) + bV, V„) = e; (Ak - Vk (a))Vj (a).(8)

Запишем (8) для другого порядка индексов:

• -m,2(V,Vk) + b(J,Vx,)=e; (Aj -Vj(a))V.(a).(9)

Умножим (8) на (-1) и прибавим к (9):

tok - to22 )(Vk, Vj) = e; (AV (a) - AjV.( a)).(10)

Умножая первое уравнение в (6) на A ¹ _j , второе на A ² _j и т. д., предпоследнее на A ⁿ _j , получим систему:

—

2   11

^to k^m1 ^Ak^Aj ⁺

C; ( Ak ^{- V}k ⁽ a ) ) ^AV ‘ 2 ( Ak ^- Ak ) A j

= 0,

- to ² m,A\A^l- + Г c^A¹, - Ai ¹ U i ,. - c.,_A Aa+ ^{+ 1} - A¹,\a¹,. k i k J L i\ k k j J    i +1 ( k k) J

- to 2 m_nAnAn +Г cJAn - An ^-1) An k ⁿ k j L ⁿ \ k k j J

= 0.

= 0,

Далее для каждого уравнения составляем пары уравнений, из которых второе записывается для индексов в другом порядке, а затем в каждой паре первое умножаем на (-1) и складываем со вторым.

В результате получим систему уравнений:

( to k - to j ² ) m _;A k A j + C _; ( V k ( a ) A j - V(a ) A^; ) +

^{+ c} 2 ( ^A k A l ^- A J A k ) = 0,

⁽ to k ^- to 2) AkA2 + c 2( AkA ^{2 -} A ^j. Ak ²) ⁺

^{+ c} 3⁽ Ak Aj- A 3j^A2⁾ = 0,

^{( to} k ^{- to} 2) A3 A ^{j +} c j⁽ Ak Aj” AJAk ⁺

+ c. ( A 4 A ³ - A ⁴ A ³) = 0, 4 k        k

₍ ω _k 2 - ω 2 _{j ) Ak} n - 2 _A n _j - 2 + _{cn - 2( Ak} n - 3 _Aj n - 2 - _A n _j - 3 _Ak n - 2 ₎ +

+ _{cn - 1( Ak} n - 1 _A n _j - 2 - _A n _j - 1 _Ak n - 2 ₎ = _0,

₍ ω _k 2 - ω 2 _{j ) Ak} n - 1 _A n _j - 1 + _{cn - 1( Ak} n - 2 _Aj n - 1 - _A n _j - 2 _Ak n - 1 ₎ +

+ c n ( A kⁿ A ⁿj ^{- 1} - A ⁿj A k^{n - 1} ) = 0, ( ω k ² - ω ² j ) A kⁿ A ⁿj + c n ( A k^{n - 1} A jⁿ - A j^{n - 1} A kⁿ ) = 0.

Складывая последовательно в полученной системе каждое уравнение с последующим начиная снизу и в последнюю очередь с первым, с учетом (10) получим:

( ω k ² - ω ² j )( m 1 A k ¹ A ¹ j + m 2 A k ² A ² j + ... + m n A kⁿ A jⁿ + ρ F ( V k , V j )) = 0.

Отсюда при k ≠ j получим условие ортогональности:

m 1 A k ¹ A ¹ j + m 2 A k ² A ² j + ... + m n A kⁿ A jⁿ + ρ F ( V k , V j ) = 0.             (12)

3 Решение начально-краевой задачи

Решение гибридной системы дифференциальных уравнений (1) будем искать в виде:

m_i z_i ( t ) =∑ ϕ _k ( t ) A_kⁱ , i = 1,2,..., n , k = 1

m u ( x , t ) =∑ ϕ _k ( t ) V_k ( x ). k = 1

Начальные условия:

m

∑ ϕ _k (0) A_kⁱ = z_{i 0}, i = 1,2,..., n , k = 1

m

∑ ϕ _k (0) V_k ( x ) = ϕ ( x ), k = 1

m

∑ ϕ _k ′ (0) A_kⁱ = z_i ′ ₀, i = 1,2,..., n , k = 1

m

∑ ϕ _k ′ (0) V_k ( x ) = ψ ( x ).

k = 1

Запишем уравнение (5) в виде:

ϕk′′(t) +ωk2ϕk(t) =0, которое имеет решение

. „ Фм .

Ф (t) =     sin (У, t + Ф Acos(У, t, k      kk0 k

k где Фк0 * Фк (0), ^к 0 Найдем Фко,фо

_ Ф _к (0).

, используя (15) и (16):

m

Z Ф _к (0) Ak = z ₀, i = 1,2,..., n , к = 1

m

Z Ф _к (0) V_k ( х ) = ф ( X ). к = 1

Умножим (15) на m _i Ai _j и просуммируем по i :

mnn

k ikj ii0j к = 1 i = 1 i = 1

Умножим (16) на P FVj ( x ) и проинтегрируем по x :

m

Z Фк(0)pF(Vky.) = pF(Ф,V), к = 1               J J где ll

(V, , V ,) = I V^ ( x )V /( x ) dx ,( Ф , V ,•) = I Ф ( x ) V , ( x ) dx . kj ₀ kjj ₀ j

Сложив (21) и (22), получим:

Z Ф (0)(pF(Vk, V,) + Z т.АкА\) = к = 1 к к j i = 1 z к j

n

= Z m.z. 0 Aj + p F ( Ф , Vj ), j = 1,2,..., m .

В силу условия ортогональности m, A\ Aj + m 2 A2 A2 +... + m„A;A; + pF (Vk, К,.) = 0.

В левой части (23) останется одно слагаемое при к = j, то есть nn

Ф (0)(pF(V ,V ) + Z mAA ) = Z m.z..A. + pF(Ф,V,•), J          J J I _ 1 . J J I _ 1 ..0 J           J j _ 1,2,...,m.

Отсюда nl

Z mizi ₀ Ai. + p F J Ф (x)Vj ( x ) dx

Ф (0) = ■ --------------⁰---------------, j = 1,2,..., m .      (25)

jln pF J V 2( x) dx + Z m (Ai )2

0 j i = 1 i j

Аналогично из (17) и (18) получим:

n _i l

У mz У Ai- + p F J y ( x )V ( x ) dx

1 i i ⁰ J A J

Ф . (0) =        l------------, j = 1,2,..., m .     (26)

p F J V 2( x ) dx + Z m- ( Ai )²

0 j          i = 1 i j

Имея в виду, что

V.(x) = a .(x) A1, и Ai. = A1 g.., j jj j j ij где aj (x) =

в ] V j ( x - a )

получим nl

1,-1 i i ⁰ ij A j

Ф ,.(0) =     i=^ ------------⁰-------------, j = 1,2,..., m .

^j       A ¹         l 2            ⁿ          2

j   p F J a 2^{( x} ) ^{dx +} Z m ⁽ g ,- ,-⁾²

0 j i = 1 i ij nl

Z mizi '0 gij + p F J ^ ( x ) a j ( x ) dx

Ф’ (0) =     i -^Ц------------⁰-------------, j = 1,2,..., m .        (28)

j A ¹ l 2            n          2

j    p F J a 2^{( x} ) ^{dx +} Z m ⁽ g ,-,-⁾²

0 j i = 1 i ij

Подставив (27) и (28) в (20), получим:

Ф _k ⁽ t ) =

nl

Z m^ ‘ 0gik + p F J V (x a_k ( x ) dx

1 i = 1                      0                     ■

------:--:------------------------------------Sin 69, t + m A1 l ч         n         0 k k k  pF J a2( x) dx + Z mi (gi^ )2

0 i = 1

nl

+J

Ak

Z mizi0gik + pF J ф(xak (x)dx i =1 ,--------------0--------------cos m t.

ln   k pF J «k(x)dx + Z mi (gik )2

0 i = 1

Подставив (29) в выражения (13) и (14), получим решение начальнокраевой задачи в виде:

n

l

m

Z ; ( t ) = Z (

k = 1 6

Z miz ‘ 0gik + p F J ^ x a_k ( x ) dx

" ■ ----------------⁰----sin m t +

2 k

ln k   pF J a2(x)dx + Z mi (gik)

0 i = 1

n

l

Z mizi 0 gik + p F J ф ( x a_k ( x ) dx

+gk i^1^------n------ cos mk t ’■ pF J «2(x)dx + Z mi (gik )2

0 i = 1

n

l

m u (x, t) = Z (■ k = 1

, x Z mz ‘_n g., + p F J v ⁽ x a ⁽ x ) dx a k ^{( x} ) i = 1 i i ⁰ ik 0 k

ω

k

n

ln pF J a2(x)dx + Z mi (gik )2

0 i = 1

l

Sin 69, t + k

Z mizi 0 gik + p F J ф ( x a_k ( x ) dx

+ a, ( x ) i ^¹—:-------------⁰-------------cos 69, t ).

klnk pF J ak( x) dx + Z mi (gi^ )2

0 i = 1

Заключение

В работе поставлена задача на собственные частоты для рассматриваемой механической системы, указан способ получения уравнения на частоты и форм собственных колебаний. Впервые выведено условие ортогональности и решена начально-краевая задача, то есть выведены явные формулы для смещений точек оси балки в зависимости от их координат и времени, а также смещений произвольного числа твердых тел, образующих каскадную систему в зависимости от времени в виде конечных рядов. При фиксированных физических параметрах механической системы, решение начально-краевой задачи будет зависеть от краевых условий на концах балки, а также задаваемых начальных условий. В дальнейшем планируется создание программного комплекса для численного определения частот и форм собственных колебаний, а также на основе этого, решение начально-краевой задачи.

Планируется доказательство единственности обобщенного решения поставленной начально-краевой задачи и на основе выведенного условия ортогональности путем введения гильбертовых пространств доказательство сходимости обобщенного решения.