Решение одной задачи оптимального распределения ресурсов

Рассмотрим следующую задачу оптимального управления:

T

Ф ( u ) = J e ^Y t (1 - u ( t )) x ⁶ ( t ) dt ^ max, u е V ,          (1)

x = a ux ⁶ ,      x (0) = x 0 ,

V = { u ( • ) е C([0; T ]), u ( t ) е [0;1], t е [0; T ]}.

Здесь t е [0, T ] — время, u ( t ) — управление, x ( t ) — фазовая траектория, С([0, T ]) — пространство кусочно-непрерывных функций на [0, T ],

V — множество допустимых управлений. Выделим параметры задачи (1): Y ; a >  0 ; s е (0,1); x ₀ >  0; T >  0 .

В содержательной интерпретации данная постановка представляет собой упрощенный вариант общей задачи распределения ресурсов в двухсекторной экономической модели специального вида [1; 2]. В свою очередь, частный случай задачи (1) при у = 0, s = 1 (билинейная задача оп тимального планирования инвестиций) хорошо изучен в литературе и часто представляется в качестве методического примера использования принципа максимума.

В этом случае оптимальное управление имеет вид и *( t)

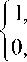
t е [0, т ), t е ( т , T ],

с точкой переключения т = T --.

a

В данной статье для рассмотренной нелинейной задачи (1) найдены условия на параметры, при которых оптимальное управление сохраняет указанную структуру без появления особых участков магистрального ти -па. При этом точка переключения т является единственным корнем нелинейного уравнения, которое представляется в виде, удобном для итераций. Сохраняются привычные условия на конечный момент T : долгосрочное планирование ( т е (0, T )) и «малые» T ( т = 0).

Результаты аналогичного характера представлены в [3-7].

u * ( y , x , t ) =

0,

1,

g ( y , t ) x ^E <  0, g ( y , t ) x ^E >  0.

Если g ( y , t ) x ^E = 0, то u * ( y , x , t ) e [0; 1].

Проведем упрощение этой формулы с учетом характера фазовых тра-екторий. Пусть и ( • ) e V — произвольное допустимое управление.

Соответствующее фазовое уравнение имеет вид

x ( t ) = a u ( t ) x ^E ( t ), x (0) = x 0

Его решение представляется формулой x (t) =

t x 0-E + (1 - e )a j и (т) dr

1 - E

t e [0; T ] (4)

Действительно, проведем проверку:

x (0) = x ₀ ,

E

x( t )=-^-1 - E

t x 0E + (1 - e )a J u (т) dr 0

1 - E

• (1 - e ) a u ( t ) = a u ( t ) x ^E ( t ).

Таким образом, формула (4) для x ( t ) справедлива. Из нее, в частности, следует, что x ( t , u ) >  0, t e [0; T ] для любого управления u ( • ) e V .

Рассмотрим формулу (3) в области x > 0. Поскольку xE > 0, то максимизирующее управление не зависит от фазовой переменной, т. е. имеет место представление

u * ( y , t ) =

/ 0, 1 1,

g ( y , t ) <  0, g ( У , t ) >  0.

Если g( y , t ) = 0, то u * ( y , t ) e [0; 1].

Отметим, что u *(y, t) g (y, t) =

0,

I g ⁽ y , t ),

g (y, t) < 0, g (y, t) > 0, т. е. u*(y, t)g (y, t) = max{0, g (y, t)} = g + (y, t).

Сопряженное уравнение (2) при u = u*(y, t) принимает вид y =--^T(eyt + g + (y, t)),     y( T) = 0.          (5)

x ^{1 E}

Пусть x ( t ), t e [0; T ] — произвольная фазовая траектория, y ( t ) — решение сопряженного уравнения (5) при x = x ( t ). Тогда имеет место свойство монотонного убывания

V ( t ) = —^ — ( e ^Y + g* ( / ( t ), t )) <  ⁰,     t ^{е [0}; ^Т )•

х ( t )^{1 - 6}

Поскольку / ( Т ) = 0, то / ( t ) >  0, t е [0; Т ).

Таким образом, для любой фазовой траектории х ( t ) и H - максимизирующего управления u * ( / , t ) — соответствующее решение сопряженного уравнения монотонно убывает на [0, Т ) и положительно:

/ ( t ) <  0,      / ( t ) >  0,       t е [0, Т ).

В частности, это свойство справедливо для любого экстремального управления u ( t ) задачи (1), поскольку u ( t ) = и * ( / ( t , u ), t ), t е [0, Т ], причем

/ ( t , u ) = ⁶     ( e ^Y + g + ( / ( t , u ), t )),      / ( Т , u ) = 0.    (6)

х ( t , u ) 1 ⁶

Кроме того, отметим, что функция переключения экстремального управления

g ( / ( t , u ), t ) = a/ ( t , u ) - e ^Y ,      t е [0, Т ]

в конечный момент времени t = Т отрицательна: g( / (Т , u ), Т ) = - e^yT <  0.

С учетом ее непрерывности по t заключаем: найдется такое 5 > 0, что g(/(t, u), t) < 0,     t е (Т - 5, Т].

Это значит, что на «финишном» промежутке по времени любое экстремальное управление равно нулю.

2 Построение экстремального управления

Для некоторого экстремального управления u ( t ) рассмотрим функцию переключения g ( / ( t , u ), t ), t е [0, Т ], где / ( t , u ) — решение уравнения (6) с фазовой траекторией х ( t , u ), которая выражается по формуле (4).

dt и рассмотрим первый случай, когда параметр у положителен: у > 0 . Тогда производная меньше нуля, т. е. функция переключения монотонно убывает на отрезке [0, Т] с отрицательным значением в конечный момент Т . Выделим точку т < Т , в которой

g( / ( т , u ), т ) = 0 о / ( т , u ) =— e ^Y .

a

Предположим, что т >  0 , т. е.

g ( / ( t , u ), t ) >  0, t е [0, т ),

g ( / ( t , u ), t ) <  0, t е ( т , Т ].

В соответствии с этим соотношением введем управление

J 1, t e [0, T ), u ( t ) = \

[ 0, t G ( t , T ].

На основании формулы (4) для фазовой траектории получаем

x ( t , u )^{1 - е} = x 0 ^е + a (1 - s)т,      t g [ т , T ].

Сопряженное уравнение для t g [ t , T ] принимает вид

¥ & ⁽ t ) = ^-

"Л— ^е-----e ^Y ,    _V ( T ) = 0.

x 0 + a(1 - e ) t

После интегрирования по t g [ t , T ] получаем

V ^{( t} ) =

e ( e ^{Y T} - e ^YT )

(x 0-e + a(1 - s) т ) y кото

Точка переключения т характеризуется условием у(т) =—e a рое приводит к следующему уравнению относительно т

ae + у x 0-е + a/(1 - 8 )т = ae^(T-т).             (7)

Представим его с помощью двух функций (левая и правая части равенства)

Ф 1^{( т} ) = Ф 2 ^{( т} )•                                  ⁽⁸⁾

Функция ф1 (т) [ф2 (т)] монотонно возрастает [убывает] на [0, T], при чем ф1 (T) > ф2 (T). Предположим, что ф1 (0) < ф2 (0). Тогда уравнение (8)

имеет единственный корень т * на интервале (0, T ).

При этом управление u *( t)=J0,

t g [0, т * ), t G ( т * , T ]

является экстремальным, поскольку

g ( ^ ( t , u * ), 1 1 >  0, t G [0, t * ), g ( ^ ( t , u * ), t ) <  0, t G ( t * , T ].

Обсудим предположение ф1 (0) < ф2 (0). Фактически это условие на па- раметры задачи ае + у x0-е < a eeTT , которое обеспечивает «корректность» точки переключения т* [т* G (0, T)].

Представим это неравенство в виде

eYT > 1 + Yx0-е.

ae

Отсюда получаем условие на конечное время

1 ( У

T >— ln 11 + ^-x0—s I, (9) Y к as )

которое обычно трактуется как случай долгосрочного планирования.

Таким образом, при условии (9) управление u * ( t ) является экстремальным в задаче (1). При этом точка переключения т * есть единственный на (0, T ) корень уравнения (7).

Если условие (9) не выполнено (случай краткосрочного планирования), т. е. ф ₁ (0) >  ф ₂ (0), то уравнение (7) не имеет решений на (0, T ). Это значит, что функция переключения g ( ^ ( t , 0), t ) отрицательна на (0, T ) и экстремальное управление является нулевым: u * ( t ) = 0, t е [0, T ].

Остается заметить, что численное решение уравнения (7) при условии (9) можно проводить, например, с помощью метода простой итерации. При этом достаточное условие сходимости метода (I ф 2 ( т ) I <  1, т е (0, T )) нетрудно представить в явном виде через параметры задачи.

Рассмотрим, далее, второй случай, когда параметр у отрицателен: Y < 0 . Будем рассуждать в рамках той же схемы относительно функции переключения g(^(t, u), t) с экстремальным управлением u(t). В данном случае с учетом сопряженного уравнения dg(^(t, u), t) = aw(t, u)+1 у |eY = dt

(

= I Y I к

Отметим, что

—

as x (t, u )1—s ,

e

Y t

—

—^as g ₊ ( И t , u ), t ). x ( t , u ) 1

x ( t , u ) >  0,       g + ( ф (t , u ), t ) >  0,       t е [0, T ].

Поэтому отрицательность производной — обеспечивается условием dt

। as t е[0, T ].

I Y I <----------1ZT", x (t, u )1

На основании формулы (4) имеет место оценка сверху x ( t , u )^{1 — s} <  x 0 ^Е + a (1 — s ) t <  x 0 ^s + a (1 — s ) T .

В результате получаем итоговое условие на параметр у

Y <  0, Y I<    -------------,           (10)

x 0 + a(1 — s) T которое гарантирует монотонное убывание функции переключения g(y(.t, u), t) на [0, T].

Далее действуем по аналогии с предыдущим случаем ( y >  0) вплоть до уравнения (7) в интерпретации (8).

В рассматриваемом случае (у < 0) функция ф1 (т) [ф2 (т)] монотонно убывает [возрастает] на [0, T], причем ф1 (T) < ф2 (T).

Проверим, что при условии (10) на у

Ф1(0) = as + уx0 s > 0.

Действительно,

Ф 1 (0) = as - 1 у I x 0 — >  as

у ^{1- s x} 0

x 0 ^s + a (1 - s ) T ,

> 0.

Далее внесем предположение ф 1 (0) >  ф ₂ (0), которое гарантирует существование и единственность корня т * уравнения (7) на (0, T ), что определяет экстремальное управление u * ( t ).

Это предположение приводит к неравенству на параметры

Y^{T Y} 'г^ ) e < I 1 x 0 I .

V as )

Отсюда получаем условие на конечное время (долгосрочное планирование)

T >  — ln ( 1 - ^Y x 0 ^{- s} I .

IYI V as )

Итоговые утверждения по поводу экстремального управления u * ( t )

сохраняются.

В заключение прокомментируем особый случай у = 0, когда экспонента уходит из рассмотрения. При этом свойство монотонности функции переключения очевидно выполняется. Точка переключения т определя- ется условием ^(т) = —, причем

a

s (T - т) ¥(т ) = -1------------.

x 0 + a (1 - s ) т

Отсюда получаем явное выражение для экстремальной точки

т * = — ( as T - x0^{- s} ).

a

Требование т * >  0 приводит к условию долгосрочного планирования

T > — x 0- ^s .

as условия оптимальности типа принципа максимума, полученные в [10; 11] на основе точных формул приращения функционала.

В задаче (1) экстремальное управление определяется условием и *( t) =

• 1,    g( у (t , и * ), t ) x ( t , и * ) ^E >  0, 0, g ( у ( t , и * ), t ) x ( t , и * ) ^E < 0.

Поскольку x ( t , и ) >  0, t e [0, T ] для любого управления и е V , то в предыдущей формуле можно заменить траекторию x ( t , и * ) на любое решение x ( t , и ) фазового уравнения. Это значит, что управление и * ( t ) является сильно экстремальным в задаче (1) [10].

Рассмотрим далее функцию Понтрягина H( у , x , и , t ) для у = у ( t , и * ), и = и * ( t )

H ( у ( t , и * ), x , и * ( t ), t ) = x ^E [ ау ( t , и * ) и * ( t ) + e ^Y (1 - и * ( t ))].

Поскольку у ( t , и * ) > 0, и * ( t ) е [0,1], то коэффициент при x ^E положителен V t е [0, T ].

Это значит, что функция H( у (t , и * ), x , и * ( t ), t ), V t е [0, T ] вогнута по x в области R ₊ = { x >  0}, содержащей все фазовые траектории.

В совокупности заключаем, что первое достаточное условие из [10] выполнено, т. е. построенные экстремальные управления являются оптимальными в задаче (1).

Заключение

На основе принципа максимума проведено исследование обобщенной задачи оптимального планирования инвестиций. Получены условия на параметры, при выполнении которых экстремальное управление не содержит особых участков и сохраняет релейную структуру с одной точкой переключения. Обосновано свойство оптимальности полученных управлений.