Решение задачи о максимальном потоке через сеть (оптимизация временных затрат)

Задача о максимальном потоке в сети изучается уже более 60 лет, что связано с огромной практической значимостью этой проблемы. В частности, она может быть использована для определения теоретических показателей дебита нефти в контрольных точках сети нефтепровода. Эта задача имеет важное практическое значение, так как не только позволяет определить факт недостачи нефти в процессе прохождения ее по нефтепроводу, но и локализует место потери в окрестности определенных контрольных точек, что позволяет более эффективно искать причину недостачи и устранять ее. Одним из требований, предъявляемых к программной реализации поставленной задачи, является требование получение решения за время, не превышающее 2–3 мин.

1.    Выбор алгоритма решения

Задача о максимальном потоке является классической задачей дискретной математики, для решения которой разработано и разрабатывается много алгоритмов. Авторами были рассмотрены и реализованы в виде про

граммного кода наиболее известные методы решения задачи о максимальном потоке:

• 1.    алгоритм Форда–Фалкерсона,

• 2.    алгоритм Диница,

• 3.    алгоритм Карзанова,

• 4.    алгоритм Голдберга–Таряна,

• 5.    алгоритм Голдберга–Рао.

Были проведены сравнительный анализ алгоритмов и исследование эффективности их работы по времени. По результатам проведенного исследования были сделаны следующие выводы:

• 1.    Алгоритм Диница можно использовать для сетей только с определенной топологией, так как он состоит из фаз, на которых поток увеличивается сразу вдоль всех кратчайших цепей определенной длины. Анализ показал, что если топология сети такова, что значительное число цепей в сетях имеют одинаковую длину, то нежелательно использовать данный алгоритм для решения задачи о поиске максимального потока.

• 2.    Время, затраченное на получение результата с помощью алгоритмов Карзанова и Голдберга–Рао, значительно меньше времени, затраченного на алгоритм Форда–Фалкерсо-на. Необходимо отметить, что для сетей с не-

• большим количеством вершин алгоритм Кар-занова является более эффективным, но на достаточно больших сетях алгоритм Голдберга–Рао имеет лучшие показатели по временным затратам.

• 3.    Необходимо отметить неприемлемое время расчетов по всем алгоритмам на сетях с большим количеством вершин (порядка нескольких сотен).

Для сокращения времени решения задачи о максимальном потоке применено распараллеливание вычислений. Самым удобным для распараллеливания оказался алгоритм "Проталкивание предпотока" Голдберга [3, 4]. Выбор алгоритма был обусловлен следующими причинами:

• 1.    Этот алгоритм является одним из наиболее быстрых из известных алгоритмов поставленной задачи (оценка алгоритма O(V²E)).

• 2.    Его структура позволяет выполнить распараллеливание на выбранном языке программирования (ABAP) без дополнительных затрат на синхронизацию.

• 3.    Для него можно получить прозрачную схему распараллеливания.

2.    Общие идеи алгоритма 3.    Исследование эффективности распараллеливания

Соблюдения закона сохранения потока в процессе работы алгоритма не требуется. Достаточно, чтобы выполнялись свойства предпотока. Будем называть предпотоком (preflow) функцию f :V x V ^ R , которая кососимметрична, удовлетворяет ограничениям, связанным с пропускными способностями, а также ослабленному закону сохранения: ƒ(V,u) ≥ 0 для всех вершин u Є V \ {s}. Таким образом, в каждой вершине u (кроме истока) есть некоторый неотрицательный избыток (excess flow) e(u) = ƒ(V,u).

Вершина (отличная от истока и стока) с положительным избытком называется переполненной (overflowing). В алгоритме проталкивания предпотока избыток жидкости в каждой вершине (месте соединения труб) сливается. Кроме того, важную роль играет целочисленный параметр, который будет называться высотой вершины. Предположим, что в процессе работы алгоритма вершина может подниматься вверх. Высота вершины определяет, куда мы стараемся направить избыток жидкости: хотя (положительный) поток жидкости может идти и снизу вверх, увеличивать его в такой ситуации нельзя.

Высота истока всегда равна |V|, а стока – нулю. Все остальные вершины изначально находятся на высоте 0 и со временем поднимаются. Для начала отправляем из истока вниз столько жидкости, сколько нам позволяют пропускные способности выходящих из истока труб (это количество равно пропускной способности разреза (s, V\s)).

Рассматривая какую-нибудь вершину в ходе работы алгоритма, можно обнаружить, что в ней есть избыток жидкости, но что все трубы, по которым еще можно отправить жидкость из чего-то и куда-то (все ненасыщенные трубы), ведут в вершины той же или большей высоты. В этом случае можно выполнить другую операцию, называемую "подъемом" вершины u. После этого вершина становится на единицу выше самого низкого из ее соседей, в который ведет ненасыщенная труба – другими словами, вершина u поднимается ровно настолько, чтобы появилась ненасыщенная труба, ведущая вниз.

В конце концов, можно добиться того, что в сток приходит максимально возможное количество жидкости (с учетом пропускных способностей труб). При этом предпоток может еще не быть потоком (избыток жидкости сливается). Продолжая подъем вершин (которые могут стать выше истока), мы постепенно отправим избыток обратно в исток (что означает сокращение потока жидкости от истока) и превратим предпоток в поток (который окажется максимальным).

Анализ структуры алгоритма выявил его следующую особенность: основная часть времени (примерно 90%) тратится на проверку (поиск) вершины или дуги, для которых возможны операции подъема или проталки- вания. Основные же операции эквивалентны изменению нескольких записей в таблице, т.е. для сервера это несколько элементарных операций, в то время как проверка (поиск) – это обход всей таблицы вершин и дуг. Учитывая, что процесс поиска можно производить отдельно для части сети и нет необходимости менять данные в таблицах, то не возникает конфликта на уровне данных. Проверку (поиск) можно запускать для части сети ассин-хронно и синхронизировать только момент завершения работы.

Для проведения вычислительных экспериментов в ERP системе SAP R3 была создана программа на АВАР/4. Особенность этой системы заключается в том, что распараллеливание можно производить на нескольких серверах.

Следует отметить, что все вычислительные эксперименты проводились при нормальной загрузке серверов, то есть в рабочее время, когда каждый сервер работал в мультизадачном режиме, и одновременной работе в системе более 100 пользователей.

Для оценки эффективности распараллеливания программа тестирования была запущена на 1, 2, 4, 8, 16 серверах в последовательном и параллельном режимах. Запуск программы в последовательном режиме на двух и более серверах означает, что вся программа выполняется на одном сервере, но создаются сессии на других серверах в количестве, необходимом для запуска программы в параллельном режиме. Количество внутренних вершин изменялось от 4 до 64 при плотности сети 50%. Для каждого значения внутренних узлов проводилось по 100 испытаний программы.

Оценивалась эффективность распараллеливания сетей с 16, 32, 50 внутренними вершинами.

Для этого вычислялось ускорение вычислений:

T

S ( N ) = — - по результатам экспериментов; T N

S

полуэмп

( N ) =

– по полуэмпириче-

N t  t

— + - +

TT

t

T

N

ской формуле, где

N – количество процессоров, T – время выполнения всей программы на одном сервере, T N – время выполнения на N серверах всей программы, t

– доля времени выполнения последова- тельного кода программы одним процессом к общему времени выполнения программы,

t

1 — — - доля времени выполнения парал- лельного кода программы одним процессом в общем времени выполнения про- граммы на одном сервере,

N t

T

– доля времени порождения N про- цессов в общем времени выполнения про- граммы,

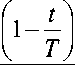
N

– доля времени выполнения па- раллельного кода программы на N серверах в общем времени выполнения про- граммы.

τ – подгоночный параметр, он определен при поиске решений при ^ d r ^ 0.

d T N

(     seqeq

T N

\

N • S

полуэмп у

• а

,

где σ – среднеквадратическое отклонение

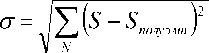
Результаты решения представлены на рис.1–6.

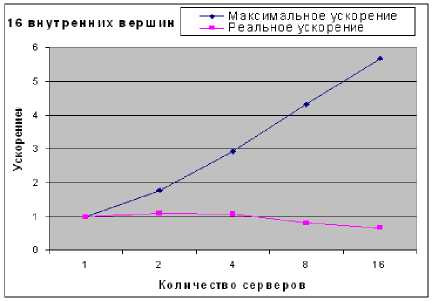
Рис. 1. Максимальное и реальное ускорение для сети с 16 внутренними вершинами

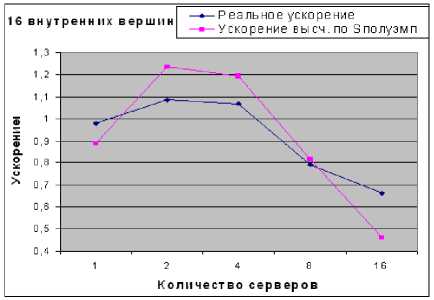
Рис. 2. Реальное и вычисленное по полуэм-пирической формуле ускорение для сети с 16 внутренними вершинами

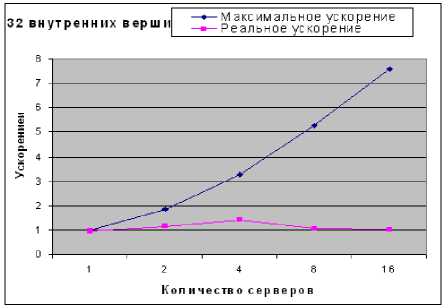
Рис. 3. Максимальное и реальное ускорение для сети с 32 внутренними вершинами

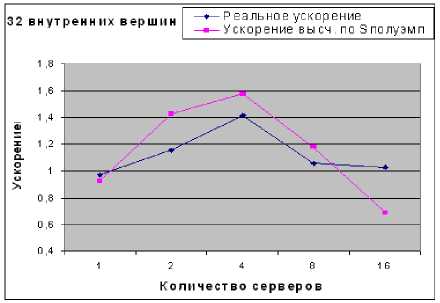
Рис. 4. Реальное и вычисленное по полуэм-пирической формуле ускорение для сети с 32 внутренними вершинами

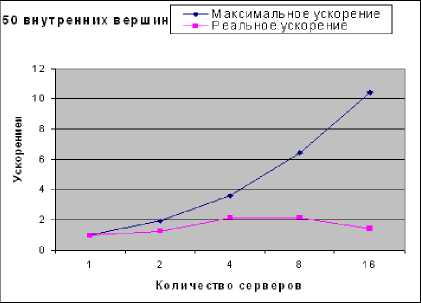
Рис. 5. Максимальное и реальное ускорение для сети с 50 внутренними вершинами

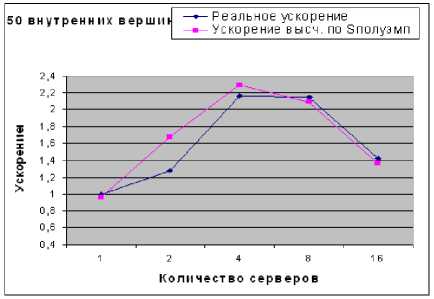
Рис. 6. Реальное и вычисленное по полуэм-пирической формуле ускорение для сети с 50 внутренними вершинами

Из рис. 1 и 2 видно, что максимальное ускорение (1.08) было достигнуто при запуске программы на двух серверах.

А из рис. 3 и 4 следует, что максимальное ускорение (1.4) было достигнуто при запуске программы на четырех серверах.

Из рис. 5 и 6 видно, что максимальное ускорение (1,16) было достигнуто при запуске программы на четырех серверах, хотя ускорение, полученное для восьми серверов, отличается от максимального ускорения незначительно.

4.    Выводы

На основании полученных результатов можно сделать следующие выводы:

• 1.    Для любого количества серверов ре-

• альное ускорение намного меньше теоретиче-
• ски максимально возможного, вычисленного по формуле Амдала. Это можно объяснить тем, что в данной формуле не учитывается время, которое тратится на взаимодействие серверов.

• 2.    Полуэмпирическая формула более

удачно аппроксимирует реальное ускорение для приведенных сетей, поэтому ее можно использовать в дальнейших расчетах для вы- бора оптимального по времени варианта реализации алгоритма (последовательного или параллельного). С помощью полуэмпи-рической формулы была оценена эффективность распараллеливания  ал-

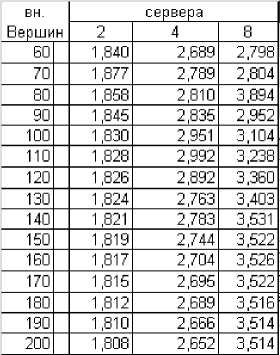
горитма для сетей с большим числом внут-

Результаты приведены таблице.

Применение параллельной версии алгоритма поиска максимального потока дает заметное сокращение времени работы программы, например, на тестовой сети месторождения с 424 контрольными точками время расчетов сократилось с 24 мин. до 5,5 мин. Этот результат хорошо согласуется с результатами, получаемыми по полуэмпирической формуле.