Решение задачи о растяжении упругой прямоугольной пластины методом быстрых разложений
Автор: Чернышов Александр Данилович, Хозяинова Наталья Алексеевна
Журнал: Вестник Воронежского государственного университета инженерных технологий @vestnik-vsuet
Рубрика: Информационные технологии, моделирование и управление
Статья в выпуске: 4 (54), 2012 года.
Бесплатный доступ
Рассмотрена постановка и решение задачи о растяжении упругой прямоугольной пластины методом быстрых разложений. Система уравнений в частных производных сводится к системе обыкновенных дифференциальных уравнений и решается методом Эйлера. Получены выражения для перемещений и напряжений.
Упругость, дифференциальные уравнения, быстрые разложения
Короткий адрес: https://sciup.org/14039932
IDR: 14039932 | УДК: 517.518.454
Текст научной статьи Решение задачи о растяжении упругой прямоугольной пластины методом быстрых разложений
В работе [1] получено решение для пластины конечных размеров методом малого параметра для упругопластической деформации, в исследовании [2] – методом граничных состояний. В [3] рассмотрено решение методом малых возмущений.
Рассмотрим прямоугольную пластину конечных размеров a х b (рисунок).
( Л + 2 ц и + Л U v ’ e x уу
O x 0 ,
Г д и д и I I ~+~ I (д у 8х )
= Ь 0 . (3) :=0, а ц
Решение задачи (1)-(3) в перемещениях
( и , и ) представим быстрыми синус -
разложениями по переменной y с граничными
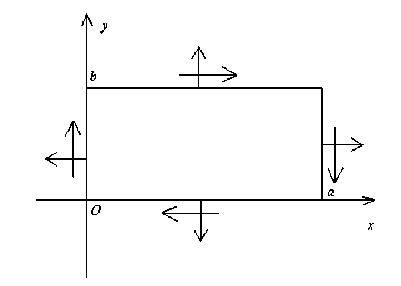
Рисунок. Прямоугольная пластина
функциями второго порядка [4]:
Г, у ) у I у 3 у • b I
и ( x , у ) = Ф 1 ( x ) | 1-T I + ^ 2 ( x Ъ + Ф 4 ( x ) | "76 —7" I +
( b v b ( 6 b 6 i
Г у 2 у 3 + № (x ) — - — 3 ( ) ( 2 6 b
U ( x , у ) = ^ 1 ( x )
у • b I ^ / \ m П m n у + > и x sin m
3 1 m = 1 ( b
| i - у I
( b )
+ V 2 ( x ) у + V 4 ( x ) | 77 - b ( 6 b
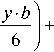
I у у у • b I v I m n у
+ v 3 ( x )I v-T^-T I+ ^ u" ( x ) sin I "T"
( 2 6 ь 3 v m = i ( ь
.
Подставим выражения (4) в систему уравнений (1)-(3), в результате чего получим
Напряженно деформированное состояние пластины описывается уравнениями равновесия Ламе:
д 2 и д^и д 2 и -
(Л + 2ц) , ; ■ I Л + ц)уГ7- + р-у = 0, дx дx ду ду (1)
д 2 и д 2 и д 2 и
( Л + 2 ц ) + ( Л + ц )—— + ц 2 = 0.
д у д x д у д x
Граничные условия (ГУ) для нормальных и касательных напряжений запишем равенствами:
( Л + 2 ц + Л ™
2 д у д x
= ° . 0 ,
у = 0, b
\ д и д и | I +^ I ( д у д x )

= ^ , (2) ц
замкнутую систему, содержащую две переменные (x, у). Чтобы избавиться от переменной у в этой системе, преобразуем уравнения в соответствии с методом быстрых разложений. Для этого левую и правую части каждого из уравнений Ламе (1) умножим на sin jпy-, j = 1..М и b проинтегрируем по у е[0, b]. В результате получим 2M обыкновенных ДУ по переменной x относительно 2М + 8 неизвестных функций, указанных в (4). Дополним эту систему, рaс-смотрев равенства Ламе на границах при у = 0, у = b. Таким образом, мы получим еще 4 уравнения. Оставшиеся 4 уравнения найдем из ГУ (2), подставляя в них выражения для пере-43
мещений (4) и затем полагая у = 0, y = b . Подобный метод использовался также в [5].
Граничные условия для напряжений зададим в виде:
^
^ xy l
I x =0
= ^ F ( У ) , ^ x L = a = ^ F 2 ( У ) , T
( n + 2 ) f v 3 ( x ) b- — v 4 ( x ) b- — u 2 ( x ) 2 ^ 2 + V 2 п 2 n b у
+ ( n + 1 ) [ — ф 3 ( x ) b- — ф 4 ( x ) b -+4 u ( x ) | + V 4 n 4 n 3 J
I x = a = ^ F 4 ( У ) , -' = 0
tJ = ^G3 (x), т I xy\y=0 r 3 V / ^"l
= ^ G 1 ( x ) , ^ = ^ G 4 ( x ) ,
I x = 0 = ^ F 3 ( У ) ,
I У = b = ^ G 2 ( x ) ,
+
v ' ( x ) b- — v 22 ( x ) b- — v *3 ( x ) /г + 2 n 2 n 8 n
= 0,
где F ’ ( x ) , G ( x ) , i = 1..4 - некоторые функции:
F ( у ) = b 1 у 2 + bi2 у + bi 3 , G i ( x ) = a i1 x + ai 2 , i = 1..4 .
Константы, определяющие напряжения на границах, зависимы между собой согласно условиям равновесия сил и моментов.
Полученную в итоге систему 2 M + 8 уравнений приведем к безразмерному виду, разделив левую и правую часть на ц . В рядах Фурье (1) ограничимся двумя слагаемыми, M = 2 , и выпишем 12 дифференциальных уравнений первого и второго порядков для 12 неизвестных функций: ф , , v i , u j , u j , j = 1,2. :
2 b 2
( Ф 1 ( x ) + Ф 2 ( x ) )—
' V " i x )+ ^ x ) b
V 8n 2 J v' (x)1+v 2 (x)1—v 3 (x) b—v 4 (x) b+
( n + 1 ) b b 36
+U (x)П + u ' ( x) —
V 1 ( ) b 2 b .
+ ( n + 2 ) ф '' ( x ) + Ф 3 ( x ) = 0, I
( n + 2 )
b 3 . b
— ( Ф 3 ( x ) + Ф 4 ( x ) )—+ u ' ( x )- П 2 у
+
f / \ 1 , f / \1 b \b b \b ,
— Ф 1 ( x )т + Ф 2 ( x )т — Ф 3 ( x )-— Ф 4 ( x ) ■
(n +1) b 6 36
. f \ n . 1 / \ 2 n
+ u , x — + u , x —
V 1 ( ) b 2 ( ) b
+ (n + 2)v3 (x) + v1’(x) = 0,(10)
— v , ' ( x ) 1 + v 2 ( x ) 1 + v 3 ( x ) b + v 4 ( x ) b —
(n +1) b b 63
П 2 П
— u. x —+ U ' x —
V 1 ( ) b 2 ( ) b
+ ( n + 2 ) ^ 2’ ( x ) + ^ 4 ( x ) = 0,
+ ( n + 1 )
2 . 2 2.
( v 2 ( x W1 ( x ) ) - -V 4 ( x ) V П 3
6 n
-
U 2 ( x ) 3
+ [ Ф 3 ( x ) - + Ф 4 ( x ) b — u 1 ( x ) П | = 0, V П П 2 b J
( n + 2 )
”( \ b ” ( A b
Ф 1 ( x h— Ф 2 ( x h— 2 п 2 П
— Ф' 3 ( x ) b r + Ф 4 ' ( x ) b r
V 8 n 8 n
, «2 \ b
+ u 2 ( x ) 2
+
+
+ ( n + i ) f — v 3 ( x ) b— v 4 ( x ) b- + 4 u 1 ' ( x ) 2 + V 4 n 4 n 3 J
+ | Ф 3 ( x ) br — Ф 4 ( x ) b- — u 2 ( x ) h r " | = 0, (6) V 2 П 2 n b J
( n + 2 ) f v 3 ( x ) b + v 4 ( x ) b — U 1 ( x ) П 2 +
V п n 2 b J
>2 —
+ ( n + 1 )
’2 - u 3 ( x ) 3
v 1 ( x ) b + v ' ( x ) b —v 3 ( x ) b y —
+
— W 4 ( x ) Ь + U 1 ’ ( x ) - П 2
= 0,
+
—Ф' ( x ) b + Ф 2 ( x ) b + Ф 3 ( x ) 6 + Ф 4 ( x ) 3 — П 2 n
— u , x —+ u ‘ x —
V 1 ( ) b 2 ( ) b J
+ ( n + 2 ) v 4 ( x ) + v 2' ( x ) = 0,
( n + 2 )
— v 1 ( x ) 1 + v 2 ( x ) b - v 3 ( x ) 3 —
, x b n xK
—V 4 ( x b+ U 1 ( x )- + U 2 ( x ) 6 b
+ПФ' ( x ) = ( a 11 x + a12 ) ,
2 n b у
— Ф 1 ( x ) 1 + Ф 2 ( x ) 1 — Ф 3 ( x ) b — Ф 4 ( x ) b + bb 36
+ u , ( x ) П + u 2 ( x ) b n + v 1 ( x ) = ( a 31 x + a 32 ) ,
( n + 2 )
— v 1 ( x ) 1 + v 2 ( x ) 1 + v 3 ( x ) b + bb 6
+ V 4 ( x ) 3 — U 1 ( x ) П + u 2 ( x )
—I
—
+ Пф 2 ( x ) = ( a 21 x + a 22 ) ,
" Ф 1 ( x ) 1 + Ф 2 ( x ) 1 + Ф з ( x ) b + Ф 4 ( x ) b — bb 63
-u 1 ( x ) n + u 2 ( x ) 2 ^ + V 2 ( x ) = ( a 41 x + a 42 ) .
2 n
у
Здесь п = — = 1.(27), для стали. Размеры Ц пластины возьмем a = 1, b = 0.4.
Полученную систему обыкновенных дифференциальных уравнений (5)-(16) будем решать методом Эйлера. Для этого представим каждую из искомых функций в виде f (x ) = f (x) + f * (x), (17) где f (x) - общее решение однородной системы; f * (x) - частное решение неоднородной системы.
В данном случае частное решение неоднородной системы следует искать в том же виде, в каком заданы правые части - то есть в виде линейной функции:
Ф* ( x ) = Ax + B i , / * ( x ) = Ai + 6 x + Bi + 6 , i = 1..4,
u * ( x ) = A j + 5 x + B j + 5 , u* ( x ) = A n x + B n, j = 1,2. (18)
Тогда первая производная каждой функции будет константой Ai, а вторая производная равна 0 . Подставим выражения (18) в формулы (5)-(16). Уравнения, входящие в систему, должны выполняться при любом x е[0, a], по этому приравняем правые и левые части уравнений при x1 и при x0. Решив обе системы, найдем Ai, Bi, i = 1..12 и дополнительные условия для напряжений на границах, необходимые для совместности системы:
G 1 ( x ) = au x + a 12 , G 2 ( x ) = an x + a 12 - ba 31 ,
G 3 ( x ) = a 31 x + a 32 ,
"Л
G. ( x ) = a3lx + a„-- .
4V 7 31 32 п + 2
Таким образом, частные решения прини мают вид:
и * ( x , у )
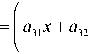
ba„ ( п + 1 ) )
y
2(п +2) У a„ (п +1) Г у2 _ у3 - у ■ b )_ a„ (п +1) Г у3 - у-Ь_ (п + 2) ( 2 6b 3 J (п + 2) (6b 6
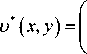
2 a п x + 2 a 12 - a 31 b ( п + 1 )
2 ( п + 2 )
a 31 ( п + 1 ) Г у 2 _ у3 _ у ■ b )_ a 31 ( п + 1 ) Г у3 _ у ■ b
( п + 2 ) ( 2 6 b 3 J ( п + 2 ) ( 6 b 6
Отметим, что полученные в процессе решения условия для перемещений у 0 | у = 0 b , r xi _об не являются ограничением общности рассмотрений, а всего лишь отражают тот факт, что пластина находится в равновесии.
Общее решение однородной системы, соответствующей системе (5)-(16), будем искать в виде:
Ф 1 ( x ) = A 1 e k , ф 2 ( x ) = A 2 e kx , ф 3 ( x ) = A 3 e k ,
Ф а ( x ) = A 4 e k , й 1 ( x ) = A e k , u ( x ) = Ae k , (19)
/ 1 ( x ) = A 7 e k , / 2 ( x ) = A 8 e k , / 3 ( x ) = A e k ,
/ 4 ( x ) = Aw e " , u ( x ) = An e k , 6 2 ( x ) = A 12 e " .
После подстановки выражений (18) в однородную систему, соответствующую (5)-(16), получим линейную однородную систему относительно постоянных Ai, i = 1..12. Приравняем к нулю ее определитель, и, решив уравнение 16-й степени относительно неизвестной к, найдем корни ki, i = 1..16. Такое количество корней в уравнении для определителя объясняется тем, что система дифференциальных уравнений состоит из ДУ первого и второго порядков, а общий порядок системы - 16.
Среди полученных решений к , ,..., к 6 - нулевые корни, к 7 , к 8 - действительные корни, к 9 , к 10 и к п, к 12 - пары противоположных по знаку мнимых корней, к 13 , к 14 и к 15 , к 16 - пары комплексно сопряженных корней. Общее решение однородной системы будет складываться из решений для каждого к .
Для нулевых корней к , ,..., к 6 решения будут представлены в виде многочленов степени i _ 1, i = 1..6 :
ф : = A ,...,u^1) = Ay для к1 = 0 , ф?: A*2)x + В1(2),...,u(22)= .12) x + b’22) для к2 = 0, ф{6) = A*6) x5 + В<6) x4 + СУ x3 + D<6) x2 + E1(6) x + F1W,
у ( 6 ) _ 2< 6 ) у5 + B( 6 ) x4 + C( 6 ) x3 + D( 6 ) x 2 + E ( 6 )% + F( 6 ) U2 "^”12 x * "^12 x * ^^12 x * ^'*'12 x * ^"^12 x * 12
для к 6 = 0 .
В этих выражениях нижний индекс константы соответствует порядковому номеру ф ~ A ,..., ф ~ A 4, u ~ A 5, и 2 ~ A 6, функции:
/ 1 ~ A 7 ,..., / 4 ~ A w, U 1 ~ A n, U 2 ~ A 12 .
Верхний индекс, заключенный в круглые скобки - номер i кратности к . = 0 , i = 1..6 .
Подставим выражения для ф 1 ( 1 ) ,..., и^ 1 в систему однородных уравнений, соответствующих (5)-(16). Поскольку к 1 = 0 обращает определитель системы в 0, после подстановки одно из уравнений системы станет линейно зависимым. Исключив это уравнение и положив A ( 1) = 1 , найдем оставшиеся коэффициенты A ( 1 , i = 2..12 и получим решения для первого корня.
Аналогичным образом найдем решения длянулевых корней к 2 ,..., к 6 .
Решения, соответствующие действительным корням, представим в виде:
ф7(7 = AP1ek 7, фр7 = A 7 7 ek 7, фр7 = Ap7ek 7, фр' = A 47 7 ek 7, u ( 7 7 = A 57 7 ek 7, u 27 7 = A p 7ek 7, /p 7 = A 77 7 e k 7, V 27 7 = A 8 7 7 e k 7, ^(77= k 7 ( 7 7 = л( 7 7 k 7 7 7 7 Л( Г ) k 7 ( 7 ) ^kk,
V 3 ^9 e , V 4 ^10 e , u 1 Л11 e , u 2 zl12 e , для k 7 . Здесь также верхний индекс в круглых скобках – порядковый номер корня k , нижний индекс константы соответствует номеру функции. То есть для корня k 8 выражения запишутся аналогично, но с верхним индексом ( 8 7 . Подставляя представления действительных корней в однородную систему, соответствующую (5)-(16), исключая линейно-зависимое уравнение и принимая одну из искомых констант Ap7 или Ap7 равной 1, найдем решения, соответствующие действительным корням.
Аналогичным образом найдем решения, соответствующие мнимым корням k 9 ,..., k 12 , представляя искомые функции в виде:
ф7 j7 = A7j7 sin (kjx^ + B7j7 cos (kjx 7, u2j7 = Ap7 sin(kjx7 + Bp7 cos(kjx 7.
Здесь j = 9..12 - порядковый номеркорня k j .
Аналогичным образом найдем решения, соответствующие комплексным корням k13,..., k14 , представляя искомые функции в виде ф( j 7 = e Re( kj 7 (A( j 7 sin (Im (kj ^x ^ + B1( j 7 cos (Im (kj ^x ^, u2j 7 = eRe7 kj7 (A^j7 sin (Im (kj ^x ^ + Bj cos (Im (kj ^x ^. Здесь j = 13..16 - порядковый номер корня kj, Re (kj 7 - действительная часть j-го корня, Im (kj 7 - его мнимаячасть.
Таким образом, общее решение однородной системы определяется по формулам:
(P1 =Z Ci ■ ф1 17,..., ф4=Z Ci' ф4 17, i=1
й1 =Y Ci. u(i, u2 =;g Ci. u (-7, i=1
-
V>1 =£ C,- V1(0,..., V/ 4 =z C,- v 4'7, i =1
-
<5, = У C ■ и<‘ 7 , бг = У C ■ и < ‘ 7 .
1i12i2 i=1
В (20) – (21) входят 16 неизвестных констант C i , i = 1..16 . Они определяются методом вариации произвольных постоянных. Для этого 46
решение в виде (17) подставим в ГУ (3), преобразованные согласно методу быстрых разложений, и в дополнительные условия равенства нулю перемещений и их производных в точке ( 0,0 ) :
и(о,о7 = о, и(о,о7 = о, и (x, у7| = о, и (x, у7| = о.
y v ’■//|x = о, у = о y7 у 7l x = о, у = о
Решив систему из (22) преобразованных уравнений (3), найдем произвольные постоянные Ci, i = 1..16 и дополнительные условия для коэффициентов b1, bi2, i = 1..4, определяющих напряжения ^,1 , т I на границах y lx=о,a xy\x=о,a x = о, x = a . Эти дополнительные условия также не являются ограничением общности рассмотрения, а являются следствием того, что пластина находится в равновесии.
После нахождения произвольных постоянных получим общее решение неоднородной системы уравнений – функции ф , , y i , u j , u j , j = 1,2. После подстановки их в (4) найдем решение поставленной задачи в перемещениях.


