Решение задачи предельного быстродействия управления движением плоского двухзвенного манипулятора

Задачи теории оптимального управления нелинейными динамическими объектами и в частности задача предельного быстродействия являются весьма трудными для решения. В статье исследуется возможность сведения задачи о возвращении схвата манипулятора на базовую траекторию наибыстрейшим образом к задаче предельного быстродействия по приведению фазового вектора линеаризованной модели манипулятора в начало координат. Такое сведение обосновывается тем, что возмущение траектории схвата, возникающее вследствие малых отклонений начального положения схвата от его базового положения, является малым. Указанный подход позволил применить методы теории оптимального управления линейными динамическими системами к решению задачи наибыстрейшего возвращения схвата на базовую траекторию. В частности, определение оптимального времени перехода свелось к реше- нию трансцендентного уравнения, а построение оптимального управления – к решению задачи математического программирования специального вида.

1. Математическая модель манипулятора

В работах [3, 4] была построена математическая модель плоского горизонтального двухзвенного манипулятора (рис. 1). Каждое

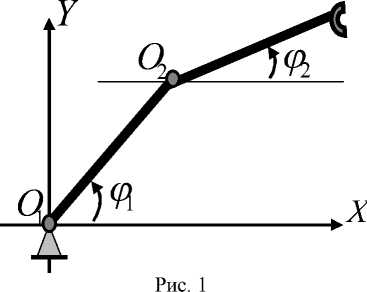
звено манипулятора представляет собой абсолютно жесткий однородный стержень длиной 1 1 = 1 2 = l и массой m i , i = 1,2 •

Первое звено соединено с неподвижным основанием вращательной парой O1 , а со вторым звеном – вращательной парой O2 . Принимается, что масса схвата манипулятора – m. В соединительных парах могут развиваться управляющие вращательные моменты, соответственно v1 и v2 . На горизонтальной плоскости, в которой расположен манипулятор, введем прямолинейную ось O1X . Обозначим через ϕi угол, образованный i -м звеном манипулятора, i = 1,2, с осью Oi X . Трение в шарнирах отсутствует. Дифференциальные уравнения движения манипулятора, записанные в форме уравнений Лагранжа второго рода, имеют вид qi = q з, q2 = q 4, bvi - bcq4 sin(q1 - q2)

'з =---------2-----2-- ab-c cos (q1 -q2)

cv ₂ cos( q 1 - q ₂)

ab - c ² cos² ( q 1 - q ₂ )

1 c ² q з ² sin^[2( q i ^- q 2 ^)] •

2 ab - c²cos²(q 1 - q ₂)

_ av ₂ + acq ₃² sin( q 1 - q ₂)

⁴     ab - c ²cos²( q 1 - q ₂)

_ ^cv i co^s( q i ^- q 2 )

i 2       2 /           ч ab -c cos (qi - q2)

+ 1 _ c²q 4 ² s^in[2⁽ q i ^- q 2 ^)]

2 ab - c²cos²(q_i - q ₂) ’

(1.1)

где

14            2     14        2

a = — (— m^ 4 m ₂ + 4 m ) l , b =—(— m ₂ + 4 m ) l ,

X = X ( t ) , Y = Y ( t ) , t g [ 1 0 , T ] , а также программные управления

^v * = ^v i * ( t ) t ^{g [} t o , T ^], i = ^i,2 , реализующие указанный закон движения. При этом движение схвата происходит по заданной (базовой) траектории Y = F ( X ) , а в моменты времени t ₀ и T схват имеет нулевую скорость. В предположении, что в начальный момент времени схват был смещен относительно базовой траектории и что это смещение невелико, в указанных выше работах была решена задача о возращении схвата на базовую траекторию до момента окончания процесса T с помощью дополнительных управлений u _i ( • ) , u ₂ ( • ) . При этом в работе [3] управления u _i ( • ) , и ₂ ( • ) были оптимальны в смысле критерия

I [ v ( • )] =

T2

J ( ui2(T ) + u22(т ) ) dT t0

(1.2)

а в работе [4] – в смысле критерия

I[u(•)] = vraimax JufT?) + и2(т).(i.3)

r e [ t o , t * ]

В книге [1] критерий (1.2) носит название "минимум энергии", а критерий (1.3) – "минимум силы". Решение задач было осуществлено с использованием линеаризованной системы дифференциальных уравнений движения схвата в окрестности базового закона движения (линеаризованная модель). Оно свелось к задаче перевода фазового вектора системы в начало координат. Сама же линеаризованная система имела вид x = A(t)x + B(t)и , (i.4) где

A ( t )	= d Q ( t , q , и ) d q		** q = q ( t ), v = v ( t )
f 0	0	1	0 1
0	0	0	i
d Q 3	d Q 3	d Q 3	d Q 3
d q i	d q 2	d q 3	d q 4
d Q	Q	d Q	d Q 4
Id q i	d q 2	d q 3	d q 4 J	** q = q ( t ), v = v ( t )

B ( t ) =

d Q ( t , q , u ) d v

**

q = q ⁽ t ), v = v ( t )

Q =

( 0     0

-QQ dvi

'Q.

I d v1    d v2 >

**

q = q ⁽ t ), ^v = ^v ( t )

(Qi ^

Q 2

Q 3

i q4;

Q i = q з ,

Q 2 = q 4 ,

q = bv i ^— bcq 4 siⁿ( q i ^— q 2 ) ³     ab — c ²cos²( q _i — q ₂)

—

cv ₂ cos( q_i — q ₂)

ab — c ² cos² ( q _i — q ₂ )

i c ² q з ² s^in[2( q i ^— q 2 ^)] •

2 ab — c ²cos²( q_i — q₂)

q   av ₂ + acq ₃² sin( q_i — q ₂)

⁴     ab — c ² cos² ( q _i — q ₂)

^cv i c^os( q i ^— q 2 ) 2      2

ab — c cos ( q i — q 2 )

+ 1 _ c²q 4 s^in[2( q i ^— q 2 )]

2 ab — c2cos2(qi — q2), a q*: [10, T] ^ R2 - закон изменения вектора обобщенных координат манипулятора, отвечающий базовому кинематическому закону движения схвата. Движение реального механизма можно получить, проинтегрировав систему дифференциальных уравнений

qi = q з, q 2   q 4, b (v* (t) + u0 (t)) — bcq4 sin(qi — q2)

q3 =  ------------2    2------------------ ab — c cos (qi — q2)

c ( v * ( t ) + u 0 ( t ) ) cos( q_i — q ₂)

—

—

—

ab — c ² cos² ( q_i — q ₂ )

i c² q 3 ^2si^n[2( q i ^— q 2 ^)]

--• --------------- Г----------Г---------------------.

2 ab — c ²cos²( q_i — q ₂)

—

(1.5)

.     av ₂ + acq ₃² sin( q _i — q ₂)

ab — c ² cos²( q_i — q ₂) ^cv i c^os( q i ^— q 2 )

7        2       2 7           4

ab — c cos ( q i — q 2 )

+ 1 _ c²q 4 ^sin[2( q i ^— q 2 ^)]

2 ab — c2cos2(qi — q2)’ с соответствующими начальными условиями.

2. Задача предельного быстродействия

В настоящей работе на основе приведенной выше математической модели манипулятора решается задача возвращения схвата на базовую траекторию за наименьшее время с использованием дополнительного управления u ( • ). Относительно управляющих пара-

метров u предполагается, что они стеснены

геометрическими ограничениями

u e P = «

f“']

I u 2 J

e R ²

u i + u 2

< a ² > .

Следуя статье [2], опишем алгоритм построения оптимального по быстродействию управления для системы (1.4). Для начального

положения { t , x } e [ 1 ₀ , T ] x R⁴ полагаем

s( t , x , T ) = max { 0, max XX '[ T , t ] l , x^ +

T

+ [min

J u e P

t

Здесь S ^{( 4 )}

( X ’[ T t ] l , B ( t ) u}dT > . (2.i)

(I

= s

l 2

l 3

1 ¹ 4 j

e R⁴

Z t=i( • i=i

X [ t ,t] — фундаментальная матрица Коши

для однородной системы дифференциальных уравнений X = A ( t ) x . Функция s называется гипотетическим рассогласованием. Ее геометрический смысл состоит в том, что величина s ( t , x , T ) представляет собой расстояние от области достижимости динамического объекта из начальной позиции ( t , x ) в конечный

момент времени T до начала координат. Известно [5], что в области s ( t , x , T ) > 0 максимум в правой части равенства (2.1) достигается на единственном векторе l ⁰( t , x , T ) e S ^{( 4 )} ,

функция гипотетического рассогласования является непрерывно дифференцируемой функцией аргументов ( t , x ) , а ее частные

производные вычисляются по формулам д80/                       0\

----( t , x ) = -( A ( t ) x , № )- min BB ( t ) u , д t^             \          ’    / u e P \          '

д8      \ 0

-T- ( t, X ) = s , дx

где s ⁰ = X ' [ T , t ] l ⁰ ( t , x , T ) .

Допустимое программное управление u ⁰ ( • ) , переводящее фазовый вектор в ту точку области достижимости, расстояние от которой до начала координат равно 8 ( t , x , T ) >  0 , удовлетворяет условию

На полуинтервале [т0,т1) управление u(0)(-) строится так, как это описано выше. Пусть x(°) (t) - решение системы дифференциальных уравнений (1.5), где в качестве дополнительного управления применяется u(0) (•). Далее полагается x(1) = lim x(0) (т). На полу-т ^Г| интервале [т0,т1) управление u'')(•) строится так же, как u(0) (•), с той лишь разницей, что в качестве начальной позиции здесь берется позиция {т1, x(1)} и т. д.

ss , B ( t ) u ⁰ ( t )^ = min ss °, B ( t ) u^ ,

t e [ 1 0 , T ] .                  (2.2)

Решение задачи быстродействия сводится к построению монотонно возрастающей последовательности

{ T k } , T >  1 0 , k = 1,2, - , 8 ( t , x , T k ) ^ 0 , удовлетворяющей условию 8 [ T_k ] >  0 . При вычислении значений ε [ T k ] , k = 1,2, - по формуле (2.1) приходится решать задачу математического программирования максимизации строго вогнутой, положительно однородной функции на единичной сфере. Данная задача осложнена наличием определенных интегралов в выражении для целевой функции, которые не берутся аналитически. При практической реализации алгоритма процесс построения членов последовательности { T_k } , k = 1,2, - следует остановить, когда

3. Численный эксперимент

Принимаем, что массово-геометрические характеристики манипулятора, а также время процесса, кинематический закон движения схвата и его начальное смещение совпадают с аналогичными параметрами из статей [3], [4]. Тогда т = m1 = m2 = 1 кг, 11 = 12 = 1 м, 10 = 0, Т = 1 сек,

Y = 1cos X +1, в = 0,000001сек, x1(0) = 1,2140-1 рад, x2(0) = 0.53 • 10-1 рад, x3(0)=0 рад, x4(0) = 0 рад сек           сек

Ограничение на управление имеет вид

u =

fu11

уu 2 у

e P = ^

fu11

уu 2 у

e R2

u 1 + u 1 <  5 • .

удается подобрать такое число T , , для кото

В принятых предположениях решается задача быстродействия по алгоритму, описанному в пункте 2. Величина гипотетического рассогласования здесь вычисляется по формуле

рого 8 [ T , ] = 0 и T , - T_k <  в, где в >  0 параметр точности. В этом случае T ⁰ e[ T_k , T , ) ,

а за оптимальное программное управление принимается функция u ⁰ ( • ) , найденная из условия (2.2).

Время перехода T ⁰ можно улучшить, если применить позиционную процедуру управления. С этой целью промежуток [ 1 ₀, T ] разбивается на полуинтервалы

8 [0, x [0], T ] = max [{ X [T ,0] x 0 , l) + ^l l 1=1

T1

+ (min[ щ ^ ( т , l ) + u₂ ф₂ ( т , l )] dт =

J u e P 1122

= mmax К X^{[T ,0] x} o ^, 0 -

[ ^ ■, ^ + 1 ) , i 0,¹, ^- , ^k , ^Т 0    t 0 , ^T k    ^T , ^T i + 1 ^T i < d .

T ______________________

-5 J 7ф|2(т, l)+^(^ l)dт , 0                                  _ где выражения ϕ1(τ,l),ϕ2(τ,l) представляют собой известные функции элементов фундаментальной матрицы Коши X [ T ,т].

Построим последовательность

{ T k } , T >  1 ₀, k = 1,2, ^ , s ( t , x , T k ) ^ 0 .

Имеем Т 1 = 0 , Т ₂ = 0.1 ,^,

T_{k - 2} = 0.4179239 , T_k- 1 = 0.417924 ,

Tk = 0.4179241, где Tk-2 - Tk < в • Тогда оптимальное время перехода Т0 = 0.417924.

Программная стратегия, удовлетворяющая необходимым условиям оптимальности, определяется по формуле u 0( t) = U (t, 10, T0) = -5

f____ 2Т 0 )____ ]

J i Tf + ^T^

^^^Р + ч^^ J

,

t е [ 1 0 , T ⁰] . (3.1)

Эффективность найденного дополнительного программного управления (3.1) проверяется путем подстановки его в исходные нелинейные дифференциальные уравнения движения (1.5) и интегрирования их с выбранными смещенными начальными условиями. Численно показано, что в результате схват в момент времени Т ⁰ выходит на базовую траекторию и продолжает движение вдоль нее после выключения дополнительных управлений.

На рис. 2 приводится базовая траектория движения схвата манипулятора и его траектория, полученная в результате решения задачи быстродействия в классе программных управлений.

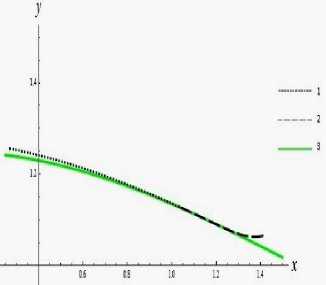
Рис. 2. Траектория движения схвата: 1 – движение схвата после его возвращения на базовую траекторию; 2 – оптимальная траектория схвата, отвечающая времени перевода Т⁰ = 0.417924 ; 3 - базовая траектория движения схвата

В момент времени Т ⁰ = 0.417924 разности между решением системы со смещенными начальными условиями и базовыми законами движения составляют соответственно A q ₁ ( T °) = 0,54 - 10 ^{- 2} рад, A q₂(T ) = 0,27 - 10 — ² рад A q₃(T ) = 3,3 • 10 ^{- 2} рад , A q ₄ ( T °) = 1,04 • 10 ^{- 2} рад сек                    сек

.

В момент времени t = 1 эта разность составляет

A q 1 (1) = 0,22 • 10 ^{- 2} рад , A q ₂ (1) = 0,24 • 10 ^{- 2} рад

,

A q ₃(1) = 0,32 • 10 ^{- 2} рад- , A q ₄(1) = 0,2 • 10 ^{- 2} рад сек                  сек

.

Далее решается задача быстродействия по схеме позиционного управления. В таблице приведены результаты решений задач быстродействия на различных участках разбиения промежутка [ 1 ₀, T ] .

Оптимальное время перехода при позиционном управлении

TiTM)	Т 0
[0;0,1)	0,417924
[0,1;0,2)	0,417457
[0,2;0,3)	0,416732
[0,3;0,416011)	0,416011

На рис.3 представлены траектории движения схвата манипулятора, получающиеся в результате позиционного управления манипулятором.

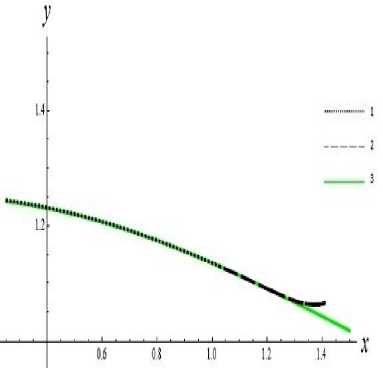
Рис. 3. Траектория движения схвата: 1 – движение схвата после его возвращения на базовую траекторию; 2 – оптимальная траектория схвата, отвечающая времени перевода Т⁰ = 0.416011 ; 3 - базовая траектория движения схвата

В момент времени Т0 = 0.416011 разности между решением системы со смещенными начальными условиями и базовыми законами движения составляют соответственно х 1( T °) = 0,38 • 10 —4 рад, х 2( T °) = 0,12 -10 -4 рад, Х3(т°) = 4,48 -10-3 рад,хс4(T°) = 7,35 -10-3 рад сек                    сек

.

В момент времени t = 1 эта разность составляет х 1 (1) = 0,25 -10-3 рад, х 2 (1) = 0,11 -10-3 рад

^, х₃ (1) = 0,93 - 10 ^{- 3} рад , х ₄ (1) = 0,18 - 10 ^{- 3} рад сек                 сек

.

Заключение

В статье показано, что программное управление, решающее задачу предельного быстродействия для линеаризованной модели, приемлемо для решения задачи о наибыстрейшем возвращении схвата манипулятора на базовую траекторию. Сравнивая качество программного и позиционного управлений, построенных в работе, можно отметить, что при позиционном управлении схват с большей точностью попадает на заданную траек- торию, а время перехода при этом меньше, чем в случае программного управления.