Решение задачи распределения температурных полей в процессе сушки зерна гречихи перегретым паром

перегретый пар, математическая модель, треугольная симметрия, температурные поля.

В последнее время в технологии сушки пищевого растительного сырья широкое распространение получило использование высокотемпературных инертных теплоносителей, в частности перегретого пара [1, 2]. Это обусловлено тем, что перегретый пар обладает существенными преимуществами перед другими теплоносителями, используемыми при термической обработке.

Разработан новый способ влаготепловой обработки зерна гречихи, целью которого является повышение энергетической эффективности влаготепловой обработки зерна путем разработки экологически чистой, ресурсосберегающей технологии. Предлагаемая технология включает пропаривание, предварительный подогрев зерна, сушку перегретым паром, охлаждение и теплонасосную установку для подготовки воздуха [3].

В процессе сушки форма зерна гречихи играет определяющую роль , поэтому важно решить задачу распределения температур -ных полей в процессе сушки зерна с формой треугольной симметрии.

В работах [1, 2] приводится решение задачи теплопроводности капиллярно-пористых материалов в условиях изотропного нагрева и испарения влаги во внешней газообразной среде.

Сайко Д.С., Шевцов С.А., 2013

Стандартные предположения состоят в том, что частица имеет форму: либо сферическую, либо цилиндрическую, либо эллип-сои-дальную. Зерно гречихи обычно имеет, преимущественно, трехгранную форму. Грани хорошо выражены, гладкие, плоские.

На рисунке 1 представлен вид необработанных зерен гр ечихи для того, чтобы убедиться, что предложенные модели весьма далеки от реальной геометрии объекта. Как предполагают авторы , учет треугольной симметрии зерна является важным моментом исследования процессов тепломассопереноса в реальном материале.

Рисунок 1 - Нешелушеное зерно гречихи

Г

8 t ( r , т )          ,г x г

—    = a A t ( r , т ) , т> 0, r eQ ; (1)

8т x ’

, Г t (r,0 ) = t0;                    (2)

• V t ( 0, т ) = 0, | t ( 0, т )| <да ;          (3)

Г a ft -t (r, т)) =’ + ^APr *, r e8Q • (4) ( c ( )) R 8 n

Здесь t , t - температуры соответственно твердой частицы и сушильного агента, а - коэффициент температуропроводности частицы, X - коэффициент теплопроводности, a - коэффициент теплоотдачи, в - коэффициент массо-отдачи, A P - разность парциальных давлений пара над поверхностью частицы и в газе, r* - удельная теплота испарения, производная вычисляется по направлению внешней норма

Г ли к границе зерна, n - единичный вектор нормали к поверхности зерна. Если зерно вписано в цилиндр, то R - его радиус, h - высота.

Введем новую безразмерную переменную:

t(r, T - t,

0 =      —- + N ,      (5)

t c ^- t 0

где параметр:

PA Pr *

N = /----V « ( t c ^- t 0 )

Число N есть безразмерная характери стика теплового потока, затрачиваемого на испарение влаги. Задача (1) - (4) примет вид:

• — = а —гу ;

8т

, Г

0 ( r ,0 ) = N - 1 , V0 ( 0, т ) = 0 ;

Лб0.0 = 0, r e8Q .(9)

a R 8 n

Далee будeм обозначать aR

Bi =     (число Био)

Рассмотрим форму зерна в виде правильной треугольной призмы. Задача о равно-

ʙeсии тpeyгольного стepжня рассматривалась ранее [4]. Однако приведенное решение не можeт быть примeʜeно нeпосрeдстʙeнно к рассматриваемой задаче, поскольку относится к решению уравнения Лапласа, а не Гельмгольца в соответствующей области. Решения с нeʜyлeʙыми граничными условиями даны в работах [5, 6], в которых задача исследуется с использованиeм различных раздeлов тeории групп. Однако оба предложенных исследова ния скорее обозначают серьезность проблемы, чем предлагают реалистичные подходы к решению поставленной задачи. В первой, в частности, предлагается решение уравнения Гельмгольца (Пуассона) с помощью финитного преобразования Фурье [5]. Решение полу-чeно в случae произвольного тpeyгольника для комбинации граничных условий Дирихлe и Неймана. Тогда как в настоящей статье гра-ничныe условия относятся к тpeтьeму типу (задача Робена). Групповой анализ, проведенный в работе [6], полезен только как информация об инвариантах преобразования группы симметрии Сз - абелевой группы с осью третьего порядка. Приведенные в статье варианты записи граничных условий ʜe могут быть прокомментированы.

Для послeдоватeльного рeшeʜия удобно ввести подходящую систему координат, отвечающую симметрии задачи. На рисунке 2 показана такая система координат в плоскости, перпендикулярной оси симметрии.

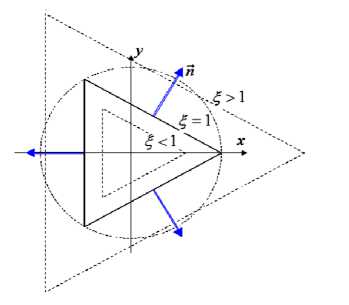
Рисунок 2 - Вид треугольной системы координат: координата η отсчитываeтся по пepимeтру треугольника. Приведены безразмерные координаты ( R = 1).

Пусть заданы функции:

/        2 х (10)

f ( x , У , ^ ) = ( ² x + ^ ) ( ( x ^- ^ ) ^{- 3} У ² ) ,    ⁽¹⁰⁾

g ( x , У , п ) = ( 2 У -п ) ( ( У -п ) ² - 3 x ² )      ⁽¹¹⁾

Переменные ^, п задаются уравнениями: f ( x , У , У = 0 , g ( x , y , п ) = 0

При такой записи новых координат по-стоянныe значeʜия пepeмeнной ξ задают равносторонние треугольники, переменная п отʙeчаeт измeʜeʜию координаты точки по периметру треугольника (на рисунке не показана). Непосредственными вычислениями

нетрудно убедиться, что метрический тензор для такого преобразования имеет вид:

22 fa x ] fd y ] 1

g _   +   _ —,

11 (a^J   (a^J     4

fa x V fa y Y 1

g„„ _       1 +       1 _ ,

22 (dn J (dn J 4

g _&a x + a y a y _ 0, g _ 1    (12)

12 a^ an a^ an          16

Следовательно, предложенная система

X"_~X , ( 2 RX ' + BiX ) _ 0 (18) R ²      x                    R

и

ее решение X ( £ ) _ cos

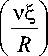
при условии на собственные значения:

2 v tg v - Bi = 0

координат является ортогональной. Диффе-

ренциальные операторы в новой системе преобразуются по следующим формулам:

Аналогичное рассмотрение по переменной z приводит к уравнениям:

Z ^-^ Z , ( - hZ ' + Bi Z ) _ 0 , h ^{2                      z} ' _ _ 0

( hZ ' + Bi Z )    _ 0

\             ^z z _ _ h

A _ V ² = 4

IX +^ 1 ^ an J

A_ 2 r JL .

d n     5^

Собственные функции этой задачи:

d ; _a_ d x ’ d y

1 a ;^ a_ _ 2 a ; _a_ Т ^ й^{,ч ;} 7 ^ 22 ^dn    к^; ^n.

^Z _ц ^{( z} w

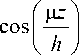
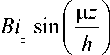
В новых координатах задача (7) - (9) примет

вид:

отвечают собственным значениям:

( ц ² - Bi ² ) tg ц- 2 Bi ц_ 0      (20)

a®   f„a ² ®   a²® a ² ®

— _ a 4 —— + 4 —— +— дт ( d^ ² dn ² d z ²

® ( £ , n , z ,0 ) _ N - 1 ;

Тогда уравнение по времени имеет вид:

T '_- a 4^ + ^ T ( R² h ² J

d® ( 0,0, z , т ) d® ( 0,0, z , т ) aa dn

_ 0;

Его решение: f f 22

T (т)_ exp - a 4— +т цvV 7 f R2

( ( ^R h J J

a z

a®

- h    I Bi ®

a®

2 R — + Bi ®

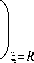
_ 0.

( a®

I h I Bi ®

(a z      ^z

_ 0.(17)

Полное решение задачи записывается в виде стандартной суммы:

®_ £X ^A .v T vW X v ( 4 ) ^Z , ( z ) ■    <²¹⁾

v ц

В постановке задачи предполагается, что

0 <^< R , 0 <  z <  h , Bi _ — ^z X

где коэффициенты определяются из начальных условий:

A nv

По симметрии задачи температура не зависит от параметра η. Поэтому задача сводится к задаче нагрева (охлаждения) прямоугольной области. Для решения такой задачи применим стандартный способ разделения пе-

—t-г Jj 0 ( 5 , z ,o ) X, (0 ^Z ( z ) d ^ dz II X v ^Z vll “

Окончательно:

ременных:

® ( z , ^ , т ) _ Z ( z ) X ( ^ ) T ( т ) .

4 Bi Bi cos v ( ц ² - Bi ² + ( ц ² + Bi² ) cos g )

A _ ( N - 1)------ ^z ----Ц--- z—Ц--- ^z!₂’ . ⁽²²⁾

^и         ( 2 v ² + Bi cos² v ) ц ^ ( ц ² + B ) - ( B + 1 ) Bi^ ² )

После подстановки:

T ' f „ X" Z" — _ a I 4-- 1--

T

XZ

получим задачу Штурма-Лиувилля

Формулы (21) и (22) с учетом вида собственных функций и уравнений на спектр собственных значений (19) и (20) являются решением поставленной задачи.

На последующих рисунках 3-5 для значений параметров N = 0, Bi = 4, Bi = 3, z h = 4/3, R = 1, a = 1 и указанных моментов времени приведены графики решений для сумм первых 20 слагаемых по переменной £ и 30 слагаемых по переменной z.

0,5              0              0,5              1

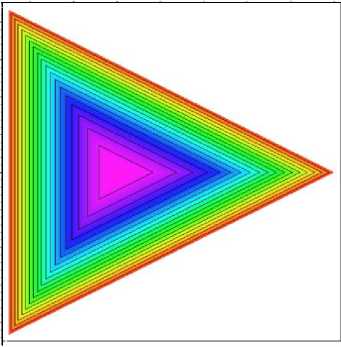
Рисунок 3 - Вид решения в декартовых координатах при т = 0.1. Выбрано значение z = 0,5 h .

На рисунке 4 приведены зависимости решения от времени при различных значениях £. На рисунке 5 показан суммарный поток тепла через боковую стенку бесконечной призмы т

Q ( т ) = Bi ph j © ( 1,0, t ) dt , где Р ^- периметр тре^- 0

угольника.

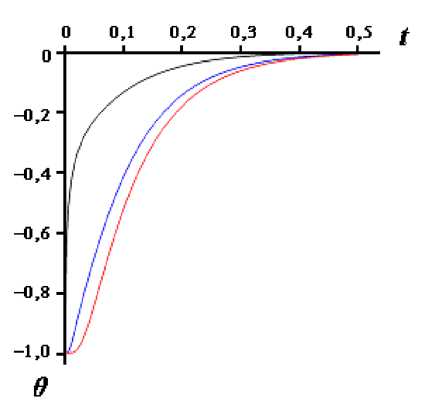
Рисунок 4 - Кривые зависимости температуры (21) от времени при ^ = {0, 0.5, 1}

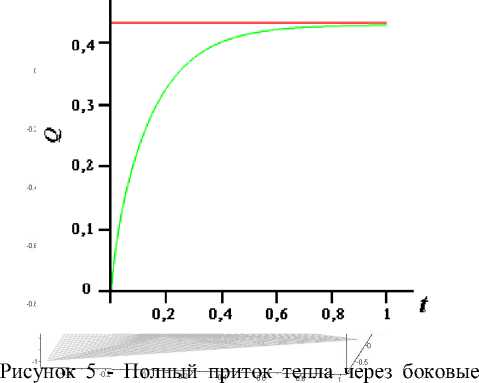
стенки как функция времени

Для сравнения было рассмотрено точное решение первой смешанной краевой задачи, полученное путем конформного отображения круга на треугольник [7]. К сожалению, граничные условия третьего рода при таком отоб ражении приводят при корректном рассмотрении к не менее сложной задаче.

Отображение задается гипергеометриче ской функцией:

f ^{( z} )

- 1.529 + 2.650 i

г (1 2 4  з )3

zF , ; , z -1.767 V--’) (3 3 3   JJ

Решение на круге записывается стандартным рядом Дини (например, [1]):

Г ² 3 ⁰

0 = ( N -1) У exp - at Н \

⁽     ^ Я R² J н J 1 ( н )

по нулям уравнения J ( н ) = 0 .

На рисунке 6 показаны результаты вычислений зависимости безразмерной темпера - туры для сечения вдоль координаты x, показанного на рисунке справа, указанных моментов времени и значений параметров.

Представлены (для соответствующих моментов времени): кривые 1, 3, 5 - для решения (21); кривые 6, 2, 5 - для решения (24); кривые 1, 4, 5. - для численного решения методом конечных элементов.

Поскольку в начальный ( t =0) и конечный ( t =1) моменты времени некоторые кривые визуально не отличаются, для них не вводились отдельные обозначения.

Приведенные результаты, на взгляд авторов, однозначно свидетельствуют в пользу того, что простое решение (21) при достаточно больших числах Био может служить для оценки распределения температур по времени и по сечению зерна.

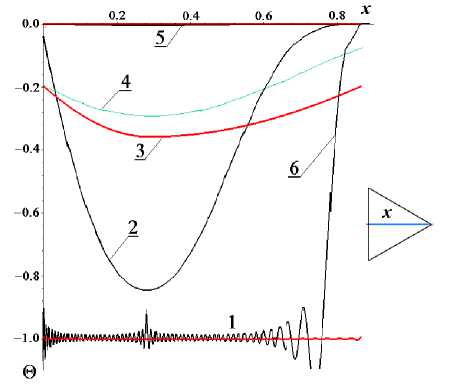
Рисунок 6 - Сравнение результатов вычислений при значениях параметров N = 0, a = 1, r = (1/V3) Bi = 3 в моменты времени t = { 0,0.1,1 } .

Сравнение полученных результатов с известными решениями [5] для треугольной области не представляется возможным, поскольку в работе рассмотрен другой вариант постановки граничных условий и отсутствуют окончательные выражения для решений в треугольнике. Вариант решения задачи, предложенный в статье [8] представляется авторам неудовлетворительным, поскольку приведенные в работе соотношения ортогональности (формула 2.11) для базиса (формула 2.10) гильбертова пространства функций заданных на правильном треугольнике не выполняются. Соответственно, построенные решения неверны.

В результате обсуждения решения, можно сделать следующие ниже выводы.

• 1.    Приведенное решение является не вполне корректным. Очевидно, что в вершинах треугольника имеет место сингулярность, которая скажется на решении. Основной проблемой здесь является преобразование потоков при обходе контура треугольника. Несложно заметить, что для функции, определенной на треугольнике, обязательным условием будет цикличность и четность по параметру п на интервале n^e ( - V3^;V3^ ) . При переходе через вершину треугольника координаты произвольного вектора v меняются по правилу V ( n = \3е ) U ^у) V ( п = -73^ ) , где U ( а ) -матрица поворота на угол а. С учетом этих замечаний, можно записать условия на преоб-

• разование координат векторов в окр естности особой точки:

• 2.    Решение задачи на собственные значения (18) по существу отвечает решению уравнения Гельмгольца в полярных координатах для сектора, ограниченного прямой линией. Такое решение хорошо известно в общем случае. Для поставленной задачи оно имеет вид exp ( Bi r cos ( ф-а ) ) , где ( r , ф ) - полярные координаты, а - угол наклона вектора нормали к прямой. Таким образом, предложенное решение несложно записать в полярных координатах.

• 3.    Решение задачи опирается на представления о сильной анизотропии пространства (в области треугольника): распространение тепла происходит только по направлению оси ^, тогда как по оси п перенос тепла фактически маловероятен.

^V n ^{( n} = ^ = 313 ^{( 2 V} ^ ^{( n} = ^ — ^v е ^{( n} = ^- ^^; (25) ^v n ^{( n} = ^{- 3 1} = ^- ^^{( v} ₆ ^{( n} = ^{3 1 + 2 v} е ^{( n} = ^{- 3 11}

Поскольку границы в уравнении (22) зависят от параметра ^, последовательный учет преобразования градиента при переходе через граничные точки усложняет решение исходной задачи.

Предложенный вариант оценки решения задачи для треугольной области выполняется при условии, когда скорость отвода тепла от границы достаточно велика для того, чтобы температура на границе выравнивалась.

Предложенный вариант приближенного решения может быть использован в качестве математической модели для исследования объектов с треугольной симметрией. По оценкам авторов, вычисление полного расхода тепла в треугольной области для предложенного решения приводит к промежуточным значениям по отношению к точным решениям в случае задания на границах треугольника условий Дирихле и Робена. Относительная простота метода и явное использование симметрии задачи моделирования также составляют его достоинство. Метод может быть распространен на случай решения трехмерных задач.

Таким образом, предложена математическая модель, аналитическое решение которой позволяет прогнозировать распределение температурных полей в процессе сушки зерна гречихи перегретым паром.