Результаты аналитического исследования температурно-влажностных параметров в картофелехранилище при контейнерном способе хранения

Для проведения аналитических исследований по определению закономерностей формирования температурных полей представим штабель из контейнеров с плодоовощной продукцией как крупнозернистое тело с равномерно распределенными по объему источниками тепловыделений q v , имеющими форму параллелепипеда. Размеры боковых граней приняты равными 2б х , 2б у , 2б z (рис. 1). Предварительно в результате натурных и экспериментальных

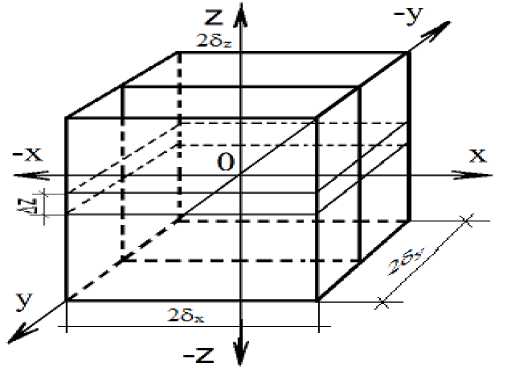
Рис. 1. Схема к расчету температурного поля штабеля из контейнеров с плодоовощной продукцией исследований системы активной вентиляции (рис. 2) был установлен достаточно равномерный характер распределения температурных полей в штабеле плодоовощной продукции и малый диапазон допустимых колебаний температур хранения [1]. Последнее позволяет пренебречь изменениями теплофизических свойств воздуха и плодоовощной продукции от температуры. Погрешность от осреднения не превышает 2-5%. Протекание теплового процесса в любой выбранной точке твердого тела в установленный момент времени описывается дифференциальным уравнением.

Уравнение теплопроводности Фурье для параллелепипеда, состоящего из изотропного материала с равномерно распределенным источником теплоты q v постоянной мощности и теплофизическими параметрами , С v , имеет следующий вид:

dt „ d ² t „ d²t    . d ² t

Ct Pt ⁼-- ⁼ ^--7 + ^--7 + ^--7 + q ^,,

T T d-Г     dx²     dy²     dz²

где t - температура тела в любой точке с координатами (х, у, z)⁰С в момент , ⁰С, т.е. t = ( х, у, z, ); q v - удельная мощность источника тепла (тепло дыхания плодоовощной продукции), Вт/м³ , определяемый по формуле Гора; τ время, ч.

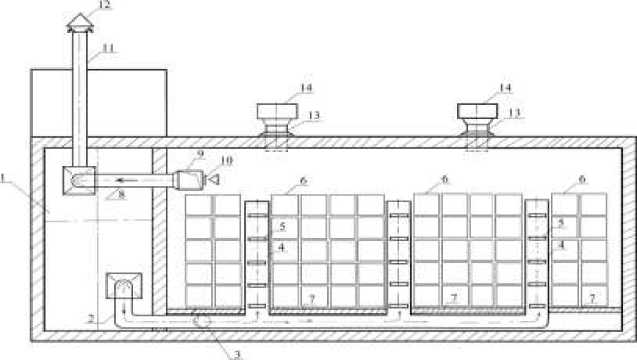
Рис. 2. Система активной вентиляции в хранилище контейнерного типа:

1 приточная вентиляционная камера; 2 магистральный приточный воздуховод;

3 – приточный воздуховод; 4 вертикальные секционные воздуховоды; 5 приточные отверстия;

6 контейнеры; 7 пол; 8 магистральный вытяжной воздуховод; 9 вытяжной воздуховод;

10 вытяжные отверстия; 11 вытяжной нагнетательный воздуховод; 12 зонт-колпак;

13 вытяжная шахта естественной вентиляции; 14 дефлектор

Контейнер с плодоовощной продукцией (параллелепипед) омывается обработанным термодинамически вентиляционным воздухом с температурой t в и в начальный момент имеет ту же температуру. В начальный момент в параллелепипеде начинают действовать источники теплоты. Начальные и граничные условия имеют вид:

при т = 0, t = tB,                   - 5 < x < +5,(2)

t/ х = 0, при х = 0, t/ у = 0, при у = 0, t/ z = 0, при z = 0 (из условия симметрии);

- ddt I dx = dvt (t - te),(3)

где х = +.

Если коэффициент теплопроводности не зависит от температуры     (t), то темпера турное поле подчиняется дифференциальному уравнению:

dt d    CT T

^л d²1 d²1 d²1) "7Г ⁺ TT ⁺ ”TT ⁺ q dx dy dz

v

I C_T p_T.

Для решения задачи, заключающейся в определении значений температур в данный момент, удобно преобразовать вышеприведенные уравнения, введя избыточную температу- ру tизб = [t (х, у, z) - tв.о], представляющую собой разность между температурой в точке (х, у, z) и температурой воздуха в объеме штабеля.

В рассматриваемой модели тепломассопереноса динамика изменения температурных полей при активном вентилировании подчиняется законам конвективного теплообмена между элементами штабеля и фильтрующим вентиляционным воздухом с учетом испарительного эффекта влагообмена, который входит неотъемлемой составной частью в коэффициент теплоотдачи vt . При этом направление теплопереноса совпадает с направленным движением воздуха. Процесс рассматривается как одномерный за счет:

равномерного по площади хранилищ расположения воздухораздающих каналов;

свободного доступа в них вентиляционного воздуха при схеме движения последнего «снизу вверх»;

термо- и гидроизоляции наружных стен;

нагревания воздуха биологическими тепловыделениями и удаления его в верхнюю зону в цикле естественной конвекции.

Результаты натурных и экспериментальных исследований позволили установить, что при активном вентилировании в объеме картофелехранилища в период основного хранения на всех поверхностях штабеля (параллепипеда) температура имеет одинаковые значения и равна температуре воздуха t в.о . Выявлено, что температура воздуха и температура продукции в локальных зонах практически разнятся на величину, численные значения которой не превышают десятых долей градуса. Поэтому можно предположить, что теплопроводность штабеля не зависит от температуры.

Тогда при стационарном режиме дифференциальное уравнение теплопроводности при- нимает вид:

d 2l>  d 2v  d 2о q„_

—^ + —^ + —- += 0.

dx   dy   dz

Пусть на поверхностях тела теплоотдача определяется граничными условиями 1 рода: v = t ⁽ x , y , z )- t eo ;

v (2 5, y, z) = v (x ,2 5y, z) = v (x, y ,2 3Z) = 0;(6)

v (0, y, z) = v ( x ,0, z ) = v ( x , y ,0) = 0, где 0 x 2 x , 0  y 2 y , 0 z 2 z .

Для определения распределения температуры в теле необходимо проинтегрировать трехмерное дифференциальное уравнение в призматической области. Решение этой задачи может быть сведено к определению специальной функции, удовлетворяющей не трехмерному, а двухмерному волновому уравнению. При этом выражение qv / шт известно и перено- сится в правую часть.

Математическое обоснование метода решения дифференциального уравнения и удовлетворение граничным условиям (6) приведены в работе [2].

Продифференцировав (5) по координате х, у, z и подставив в общее решение известное отношение q v / шт , получим формулу температурного поля в теле параллелепипеда:

v = [ t ⁽ x , y , z ) - t x ] = ^0,66 • 3_U • З_хА_Ш т ;

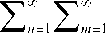
sin( 2 n - 1) Ttx 2^

sin( 2 m - 1) Tty ^y

(2 n- 1)(2 m- 1)

(2 n -1);tT 26x   _

(2 m - 1)tt ²^ y

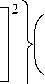
25 z

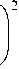
[1-(J z-z )/ 5z ].

Значение температуры в центре параллелепипеда определяется путем подстановки в уравнение (7) значения х = х ; у = у и z = z :

tц = tв.о + 0,66∙qv ∙ z / шт ∙

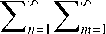
(1 -1/ ch ) {[(2 n -1> / 2^ ] + [(2 m- 1> / 25_у ]}(-1,5) ^n+m "² (1,6£_z )² (2 n -1)(2 m -1){[(2 n -1> /^ ]² + [(2 m - 1);т / 2^ ]²}

При воздухораспределении в верхнюю зону по схеме «сверху вниз» (одна из применяемых систем вентилирования) изменение температуры воздуха по высоте хранилища подчиняется линейному закону:

t пр (z) = t пр (0) + bz                                      (9)

где b коэффициент неравномерности температурных полей на высоте штабеля, 0С/м.

Анализ результатов натурных исследований показал, что увеличение температуры воздуха в основном периоде хранения составляет 0,6-1,2 ⁰С на каждый метр высоты. Так, при = 0,3 относительная температура t x = (t z t пр ) / (t см t пр ) уже на высоте z =0,50 м равна 0,023. Последнее в большей степени сказывается на формировании температурного поля в штабеле, что, в свою очередь, отражается на сохранности плодоовощной продукции.

При равномерном распределении источника теплоты с постоянной мощностью q v поле температур подчиняется дифференциальному уравнению (5).

Для рассматриваемого случая начальные и граничные условия имеют вид:

и ( x , y ,0);

и ( x , y ,2 &) = b 2 £ _z ;                              (10)

v (0, y , z ) = v(2 5_X , y , z ) = v( x ,25y , z ) = v( x ,2 5_y ,2 5_Z ) = bz .

Проинтегрировав и проведя преобразования по методике, изложенной выше, получаем следующее решение уравнения (5):

t ^{( x} , y , ^z ) = t B + b-z + ^0,66• qv-S^/ Ащт . • С•

ch {[(2 n -1>/2^] + [(2 m - 1);r/ 25_v ]}(^_z - z ) ch {[(2 n - 1)л/25_х] + [(2 m - 1)л72<^]}^

,    (11)

С

= L n- 1L m -1

sin( 2 n - 1) Try / 2<5) + sin( 2 m -1) Ttx / 2(5)

(2 n -1)(2 m -1){[(2 n - 1);r/2JJ² + [(2 m - 1);t/2^]²}(2^_z Лт)² ’

Зная температуры в любой точке с координатами х, у, z и у основания штабеля, можно определить значение избыточной температуры t изб .

На рисунке 3 представлены результаты расчета избыточной температуры вентиляционного воздуха в массе картофеля по высоте контейнера, находящегося во 2-м ряду, определенной экспериментально, при натурных исследованиях (зависимость 1) и полученных выражениях 12. Погрешность между теоретическими и экспериментальными значениями избыточной температуры не превышает 5⁰С. Подставив в уравнение (11) значения х = x , у = у , z = z , получим формулу для определения температуры в центре плодоовощной продукции штабеля (параллелепипеда):

t ц = (t в ^н + b z ) + 0,66 q v ∙ z ²/ шт ∙

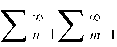
(_1,5) ^m+ⁿ -²[1 _ 1 / ch {[2 n - 1];r / 25_x + [(2 m - 1);r / 25_y ]}^_z ](tt / 2^_z)² (2 m - 1)(2 n -1){[(2 n - Х)тт/25_х]^г + [(2 m - 1);r / 2^]²}

.

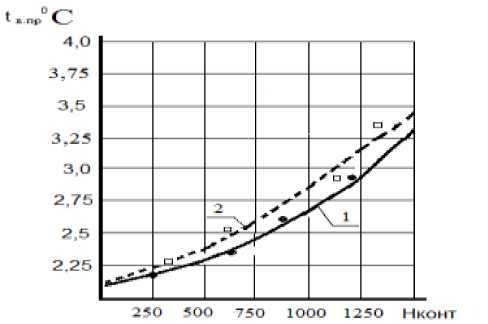
Рис. 3. Изменение избыточной температуры вентиляционного воздуха в массе плодоовощной продукции (картофеля) по высоте контейнера:

1 экспериментальные данные; 2 значения температуры, полученной по выражению 12

В результате экспериментальных исследований установлено, что изменение температуры приточного воздуха t пр оказывает влияние на формирование температурных полей в штабеле с плодоовощной продукцией. Период охлаждения заканчивается установлением в основной массе штабеля линейно нарастающего профиля температуры. При длительном хранении плодоовощной продукции изменение температурных полей носит постоянный характер в связи с наличием в картофелехранилищах системы вентиляции, обеспечивающей распределение вентиляционного приточного воздуха непосредственно в межконтейнерном пространстве и в массе продукции.