Rough Fuzzy Relation on Two Universal Sets
Автор: Xuan Thao Nguyen, Van Dinh Nguyen, Doan Dong Nguyen
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 4 vol.6, 2014 года.
Бесплатный доступ
Fuzzy set theory was introduced by L.A. Zadeh in 1965. Immediately, it has many applications in practice and in building databases, one of which is the construction of a fuzzy relational database based on similar relationship. The study of cases of fuzzy relations in different environments will help us understand its applications. In this paper, the rough fuzzy relation on Cartesian product of two universe sets is defined, and then the algebraic properties of them, such as the max, min, and composition of two rough fuzzy relations are examined. Finally, reflexive, α-reflexive, symmetric and transitive rough fuzzy relations on two universe sets are also defined.
Rough Fuzzy Sets, Rough Fuzzy Relations, Similarity Relations
Короткий адрес: https://sciup.org/15010548
IDR: 15010548
Текст научной статьи Rough Fuzzy Relation on Two Universal Sets
Published Online March 2014 in MECS
Samanta and B. Sarkar have built the fuzzy rough relations on a given universe set [9]. In this paper, the above results are extended to define the rough fuzzy relations on the Cartesian product of two universe sets, and subsequently their properties are examined.
The remaining parts of this paper is organized as following: In section II, rough fuzzy sets are reintroduced. After studying the rough fuzzy relation and its properties in section III, composition of two rough fuzzy relation and inverse rough fuzzy relation are presented in section IV and section V, respectively. Last but not least, in section VI, the reflexive, symmetric, transitive rough fuzzy relations are studied. Finally, section VII proposes the similarity rough fuzzy relation.
-
II. Rough Fuzzy Sets
-
I. Introduction
Rough set theory [1] proposed by Pawlak in about 1980s, is used to handle the redundancies, uncertainties and incorrectness in data mining, as design databases [2] or information systems [3]. This theory has been well developed in both theories and applications. Along with the study of the individual properties of rough set theory, the rough set theory in combination with fuzzy set theory [4] also gains great interest of researchers and becomes a useful tool in exploring the feature selection, the clustering, the control problem, etc. The combination of fuzzy sets and rough sets lead to two concepts [5]: rough fuzzy sets and fuzzy rough sets. Rough fuzzy sets [3, 5, 6, 7] are the fuzzy sets
approximated in the crisp approximation spaces and fuzzy rough sets [5] are the crisp sets approximated in the fuzzy approximation spaces. As the construction of fuzzy relations in fuzzy set theory, rough fuzzy relationships building on rough fuzzy set theory has important implications for both theories and applications. In [8], S. Lan has built the fuzzy rough relations on Boolean algebra. By 2011, the authors T. K.
Let и be a non-empty set of objects, /? is an equivalent relation on и . Then the space (и, R) is called an approximation space. Let X be a fuzzy set on и . We define the lower approximation set and upper approximation of X, respectively aprR (X) = (х 6 U: [х]д с А-} where
Партию = йМуеи^х^У)- У G [х]д], aprR(X) = [х е U: [х]я П X Ф 0} where M5prR(X) = SUpy6UVPxb>- У е Ия),
Boundary of X , .
The fuzzy set X is called a rough fuzzy set if .
The Cartesian product of two rough fuzzy sets X and У is
XxY = {(х,у):х Е и,у е И} where
P-xxY^x.y) = min^Cx), дг(у)}
-
III. Rough Fuzzy Relation and Its Properties
In this section, we suppose that U,V are two nonempty universal sets and Ru^v are equivalent relations on U,V respectively. Then R — Ru X Rv is a equivalent relation on U XV where
Definition 3.1. Let X.Y be the rough fuzzy sets on
U.V , respectively. We call ^cUxV is a rough fuzzy relation on U XV based on the X XY if it satisfy
(RFi) ^Uy) = 1, for all (x,y) Е X XY where
XxY = aprRu (X) x aprRv (Y) .
(RFii) Ия Uy) = 0- for all (x,y) EUxV-XxY where XxY = apr (X) X apr ,(Y) .
‘ KU * Rv
(RFiii) 0 <^Uy) < 1, for all (x,y) ex xY— X XY .
Note that:
The conditions (RFi), (RFiii) show that XxY is a rough fuzzy set on U XV .
Likewise, the representation of fuzzy relation [10], the rough fuzzy relation can be represented by the graphs, relational tables, matrices.
Definition 3.2 . Let 91 is a rough fuzzy relation on и ХИ based on the X XY . For any real numbers А E [0,1], ^Л is called A — cut of relation 91 and it was defined following way:
^(^y) = 1 <^ R(x,y) > A
1 . 0.5 . 1 . 0.5 z„x 0.4 0.5 1 0.40.5
артя„(Х) = - + — +- + — , ^«v W="5"+T+8 + T+15" — 1 0-8 1 0-8 л— and , aPTRv^ -
0.8 1 1 0.81
- + - + -+—+ —. Here we can define a rough 6 7 8 9 10° fuzzy relation 91 by a matrix:
|
0 |
1 |
1 |
0 |
1" |
|
|
9^5 = |
0 0 |
0 1 |
0 1 |
0 0 |
0 0 |
|
.0 |
0 |
0 |
0 |
0. |
We can see that A — cut of rough fuzzy relation 91 is a crisp relation.
Now we consider some properties of rough fuzzy relations.
Proposition 3.1 . Let 911,312 be two rough fuzzy relations on и ХИ based on X XY . Then Я1ЛЯ2 where ^ t л я 2 U y) = min^s ± (x, у),Мя 2 (x, y)} for all(x,y) euxv , is a rough fuzzy set on U XV based on the XxY .
Proof.
We show that91i A S42 satisfy definition 3.1.
(RFi). Since дя ± Uy) = M«2 Uy) = 1 for all (x,y) E XxY then M-^^^x.y)^
min{^ i (x, y),^ 2 (x, y)} = 1 for all (x,y) E XxY .
(RFii). Since ^! Uy) = m«2 Uy) = о for all (x,y) e UxV-XxY then
^ хля2 Uy) = = тт {/1Э!1 U y),pa2 (x,y)} = 0 for all(x,y) E Uxv-X XY .
(RFiii): Since 0<р^г {x, y), p^ 2 (x,y) < 1 for all Uy) E X X Y - XxY then 0 < ^Я1Л«2 Uy) =
9V(Xy) = 0 <=> R(x,y) < A
min{/^ 2 (x, у),р<а 2 (x, y)} < 1 (х,у) E X X Y - XxY. □ for all
Example 3.1 . Let U = {1,2,3,4}, V = {6,7,8,9,10} be two universal sets and Ru = ^х-уУ-хКиУ if x = y (modi)} , Rv = {(z, t): zRvt if z = t (mods)} are equivalent relations on U.V respectively.
x = - + — + - + — , Y = - + — + - + —+ —
1 2 3 4 6 7 8 9 10
are rough fuzzy sets on U.V respectively.
Proposition 3.2. Let 91i,912 be two rough fuzzy relations on и ХИ based on X XY. Then91 ! V «2 where Дя 2 v я 2 U у) = тах{//я t (x, y), p^ 2 (x, y)} for all (x,y) E U X V, is a rough fuzzy set on onU XV based on theX XY
Proof.
We show that31! v Я satisfy definition 3.1.
(RFi). Since ms , Uy) = ms, Uy) =1 for all
(x,y) E X XYthen Ms,vs, Uy) = тах(мя , U y). Ms , U y)} = 1 for all
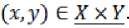
(RFii). Since Ms , Uy) = Ms, Uy) = о for all (x,y) e и xv-xxy then
V* ,vs, Uy) = = maxf/z^ Uy).Ms, Uy)} = 0 for all(x,y) e UxV —X XY .
(RFiii): Since о < ms , U y), Ms, Uy) < i for all Uy) EX XY - X XYthen 0 Lemma 3.1. If 0 < a, b< 1 then i) 0 < ab< 1 (obvious) Indeed, since 0 < a, b< 1 then a + b > 2\’ab > 2ab > ab > 0, therefore a + b — ab > 0 . On the other hand 1 — (a + b — ab) = (1 — a)(l — b) > 0 then a + b — ab< 1. The following properties of rough fuzzy relations are obtained by using these algebraic results: Proposition 3.3. Let 3li,S2 be two rough fuzzy relations on U ХИbased onX XY. Then3?! ® 31 2 where Ms, ® s, U y) = Ms, U y)- Ms, Uy) for all (x,y) EU XV, is a rough fuzzy set on onU XVbased on theX XY Proof. The relation 31 ! ®3t2 is satisfied definition 3.1. Indeed: (RFi). Since Ms , Uy) = Ms, Uy) = i for all (x,y) E X XYthen Ms,® s,Uy) = Ms , Uy)-Ms, Uy) = 1 for all(x,y) E X XY. (RFii). Since ^, Uy) = Ms, Uy) = о for all (x,y) e U XV — XxY then Ms ,@ s, Uy) = Ms, Uy)Ms, Uy) = о for all (x,y) E UxV-XxY. (RFiii): Since о < ^я 1U y), Ms, Uy) < i for all (x,y) EXxY - X XY then о < Ms,® s, Uy) = Ms, Uy)-Ms, Uy) < i for all(x,y) EXxY-XxY(Lemma 3.1 i)). □ Proposition 3.4. Let 311,312 be two rough fuzzy relations on и ХИbased onX XY. Then 3i! e 3i 2 where Ms1®s,Uy) = Ms1Uy)+Ms,Uy)- Ms, Uy).Ms, Uy) for all (x,y) E U X V, is a rough fuzzy set onUXV based on theX XY. Proof. We show that 3i! e 3i 2 satisfy definition 3.1. (RFi). Since Ms, Uy) = Ms, Uy) = 1 for all (x,y) E XxYthen Ms1®s,Uy) = Ms, Uy) + Ms, Uy) - Ms, Uy)-Ms, Uy) = i for all(x,y) EXxY. (RFii). Since ^, Uy) = Ms, Uy) = о for all (x,y) e U XV-XXY then MS,® s, Uy) = Ms, Uy) + Ms, Uy) - Ms, Uy). Ms, Uy) = 0 for all . (RFiii): Since о < Ms, U y), Ms, Uy) < i for all Uy) E XX Y - XxY then 0 < Ms,® s, Uy) = Ms,Uy) + Ms, Uy) - Ms,Uy).Ms, Uy)< 1 for all(x,y) E X XY - X XY(Lemma 3.1 ii)). □ IV. Composition of Two Rough Fuzzy Relations Definition 4.1. Composition of two rough fuzzy relations311,312 denote311 - 312 which defined on U XIVbased onX XZwhere ц^ x „ж2 (x,z) = 7пахуЕ„{т1п[/1я ± (x,у), ря 2 (y,z)]} for all(x,z) EU XW. Proposition 4.1.311 ° 3i2 is a rough fuzzy relation R onU XIVbased onX XZ. Proof. (RFi) Since 911,312 are two rough fuzzy relations on U ХИ,7 X Wbased onX XY,Y X Z, respectively. Then Дя/^УХДя,^) = 1 for all (х,у) 6 XxY and (у,z) е Y XZ. We denote Y = Щу (У) and we have M«1C«2(x,z) = maxyevtmin^^^ [Ря3 U У>, ^я , (у,^)]) = = 1 V max^-ylmin^^,*^ t (х, v), ря 2 (v,z)]} = 1 for all . (RFii) Note that Дя/^уХ^ЯзСу,^) = 0 for all (х,у) EU XV —X XYand(y.z) EV XW — Y X Z. We consider /^1O*2(x,z) = maxyey(min(:bZ)eUxiy_^9ii (x.y),^, (y,z)]} For all (x,z) EUxW-XxZ , it exists x E aprR(X) so (x, v) EU XV-XxY and Мя/^.г) = 0 for all v E V . Similarly, it exists z e aprR(Z) so (v.z) EV XW-YxZ and p^2(v,z) = 0 for all . Hence min^ezxzt^* (*. v), ^ 2 (v, z)] = 0 for all (x,z) EU XW —X XZ and v E V . So that M*t„*2(x,z) = max^fmin^^.^^Cx.y)^ = 0 for all(x,z) EUxW-XxZ. (RFiii) We must proof О < max^min^ (х,у),^2 (y.z)]} < 1 for all (x,z) e x x z — x xz. Since (x,z) 6 XxZ then at least existing xEX = aprRu (X) or zEZ = aprRw (Z) so that min ^ ± (x, y), ^ 2 (y,z) ] < 1 for all у E У . On the other hand, ^Я1(х,г) = ^2(v,z) = 0 for all (x,z) EUxW-XxZ and v E V then we have О < {тт[/1я ± (х,у),д„ 2 (y, z)]} < 1 for all (x,z) E X X Z — XxZ. and У E У . Hence, we have 0 < Tnax^vfmin^,, t (х,у),//я 2 (y,z)]} < 1 or 0< ^1o%2(x,z')< 1 for all(x,z) E X X Z — XxZ. □ Proposition 4.2. Let U, V, w, w' be the universe U X V, V X W, W X w' based onX XY,Y XZ,Z XZ*, respectively. Then ( 91i ° 912 ) - 913 = 911 ° (91 2 ° 91 3) Proof. For all x E U,y E V,z E W, t E W' we have МЯ^СЯз-Яз)^,!) = maxyer{min{/^ t (x,y),maxz€iy{min[/2S2 (y,z), дязио]}}] maxzGiy{min{max^t,{min|/i9ii(x,y~),p^2 (y,z)], ДияМ]}}) = = . □ We note that91 ! = SH2 * 91 2 = Й!, because the composition of two rough fuzzy relations 9?!,912exists but the composition of two rough fuzzy relations912,91! does not exist necessarily. V. Inverse Rough Fuzzy Relation Let X and У be the two rough fuzzy sets on и and , respectively.^IcUxV is a rough fuzzy relation on U XVbased onXxY. Then we define^CVXU is a rough fuzzy relation on V XU based onYxXas following: М-^^У.х) =Дя(х,у) for all (у, x) e v x и . Definition 5.1. The relation 94 1 is called the inverse rough fuzzy relation of 94 . Proposition 5.1. Thent^! c ^2)-l^^2"lo ^^1Proof. i) M^-^-lCx.y) = /2Я-1(у,х) = /2Я(х,у) = 1, for all (x,y) E XxY M^-ij-iCx.y) = /2Я-1(у,х) = ря(х,у) = О, for all (x,y) E Ux V-TxY sets. 911,9i2, 9i3 are rough fuzzy relations on 0< P^-i)-1^'?) = Дм-1(уа) = Дя(х,у) < 1 for all (%,у) EXxY-XxY. It means(SR1) 1 - 91. ii) For all х е и, у e v,z е w we have ^^уГ^.Х^ ^.^(x.z") = = That means(91, о ^а-^^г"1” 91Г1. □ In the same way, the representation of fuzzy relation, we can represent the rough fuzzy relation 91 by using matrix М (91). So that, the inverse rough fuzzy relation 91"1 of rough fuzzy relation 91 by using matrix М(91)£ , it is the transposition of the matrix М(91). Example 5.1. Let U = {1,2,3,4}, V = {6,7,8,9,10} be two universal sets and Ни = ^х,уУ.хНиУ if only if х = у Qmod2)3 , Ry = {(z, t):zRvt if z = t (mod3)} are equivalent relations on u,v respectively. x = - + — + - + —, Y =- + — +- + —+ — 1 2 3 4 6 7 8 910 are rough fuzzy sets on u,v, respectively. 1,0.5,1,05 0.4 0.5 , 1 , 0.4 0.5 “иаой+т+д+т ,др^и М = Т+Т + 8 + "5" + 16" 1 1— and , "P^W - 0.8 1 1 0.81 — + - + -H---h —. Here we can define a rough 6 7 8 9 10° fuzzy relation 91 as following: Let (U, Д) be a crisp approximation space and X is a rough fuzzy set on (U, Я) . We consider rough fuzzy relation in definition 3.1 in the case и = V, Ru = Rv = R, and X = Y. From here onwards, the rough fuzzy relation 91 is called rough fuzzy relation on (и, Д) based on the rough fuzzy set X. Definition 6.1. The rough fuzzy relation 91 is said to be reflexive rough fuzzy relation ifдя(х,х) = 1 for all (x,x) e и x и, hx(jx) > о. Proposition 6.1. Let 3^,912 be two rough fuzzy relation on и based X . If 911,912 are the reflexive rough fuzzy relations then 91i A 9l2, 911 V 912 , 91 ! ® 91 2 ,911®912,911-912, also. Proof. If 911,912 are the reflexive rough fuzzy relations then /1Я1(х,х),^2(х,х) = 1 for all (x,x) G U X U, HxM > 0. We have Д« 1Л«2 (^^) = min{^ t (х,х),ря 2 (x,x)} = 1 for all (x,x) 6 U X U, Hxto > 0 and 91 ! A 912 is reflexive rough fuzzy relation. P« 1V«2 (^^) = тах(^Я1 (х,х),^2 (x,x)} = 1 for all (x,x) 6 U X U, Pxto > 0 and 91i V 912reflexive rough fuzzy relation. P*!® я2(^а) ^э^Сг.хУд^Сха) = 1 for all (x,x) e U X U, nxto > 0 and 91! ® 91 2 reflexive rough fuzzy relation. Д«1@я2(^а) = Дя1(^а) + Д«2(^а)- /1Ж1(х,х)./1Я2(х,х) = 1 for all (x,x) 6 U X U, Pxto > 0 and 9?! e 912 reflexive rough fuzzy relation. m(91) = 0.5 10 0 00 0.5 10 0 00 0.6 0 0.4 0 . Then 9l-1 is an inverse rough fuzzy relation of 91, it P«1o«2(x,^) = тахуЕи{тт[^Я1(х,у),дЯ2 (y,x)]} = 1 for all (x,x) 6 U X U, Uxto > 0 and 91i ° 9l2 reflexive rough fuzzy relation. □ is represented by using matrix Af (9Г1) - M(9t)E - 0- VI. The Reflexive, Symmetric, Transitive Rough Fuzzy Relation In this section, we consider some properties of rough fuzzy relation on a set, such as reflexive, symmetric, transitive properties. Definition 6.2. The rough fuzzy relation 91 is said to be α-reflexive rough fuzzy relation where к= ™"[ЯаяСр к. if Дя (^i-y) =oci for all (x„y) eu хи, у e Мд and p.x(x) > о. Proposition 6.2. Let 911,912 be two rough fuzzy relation on и based X. If9li,9l2 are the α-reflexive rough fuzzy relations then91i A 9l2,91i V 912also. Proof. If9li,9l2 are the α-reflexive rough fuzzy relations then P« t (^i-y) = P«2 (^,y) =K where if for all and . We have ^ хл«2 fey) = minfe, (х<.у).Дя2 fey)} =к where if for all and for all and α-reflexive rough fuzzy relation. Дя 1V«2 fey) = maxfe t fey),дЯг fey)} =« where if for all and for all and α-reflexive rough fuzzy relation. Definition 6.3. The rough fuzzy relation is said to be symmetric rough fuzzy relation if for all . We note that if is a symmetric rough fuzzy relation then matrix is a symmetric matrix. It is easy to see that: Proposition 6.3. Let be two rough fuzzy relations on based rough fuzzy set. If are the symmetric rough fuzzy relations then , , ,also. Definition 6.4. The rough fuzzy relation is said to be transitive rough fuzzy relation if. Table 1: A decision system . 0.1 , 0.2 , 0.4 , 1 , 1. We consideris a ul u2 u3u4 u5 fuzzy set in . We compute 01 02 . 0 4 . °-4 . 1 r - ul u2 u3 u4u5 ------- 0.1 , 0.2 , 1 , 1 ,1 . r R ul u2 u3 u4u5 It is easy that , so is a rough fuzzy set on . We can put ;, if i, j = 1,2 and 3 =:: ^.ii-:: vj '. < 1 in the other cases. ■ 0 0 r13 r14 r15 0 0 r23 r24 r25 M ( ^ F ) = r31 r32 r33 r34 r35 r41 r42 r43 r44 r45 _ r51 r52 r53 r54 1 According the definition 3.1 we have is a rough fuzzy relation on based on VII. Similarity Rough Fuzzy Relation Definition 7.1. The rough fuzzy relation on based on the rough fuzzy set is called a similarity rough fuzzy relation if it has the reflexive, symmetric, transitive. Definition 7.2. The rough fuzzy relation on based on the rough fuzzy set is called a α- similarity rough fuzzy relation if it has the α-reflexive, symmetric, transitive. Now, we consider an illustration example. Example 7.1. We consider the decision system in Table 1. In which is the collection of condition attributes and is the decision attribute. Note that, the fuzzy set „ 0.1 , 0.2 , 0.4 , 0.4 , 1 . t- is not the rough fuzzy 1 ul u2 u3 u4 u5 set on U because X 01 0 2 0 4 . °'41 r - 1 ul u2 u3 u4u5 ------ Л 01 0'2 0'4 I 0'4 I 1 =. " R 1ul u2 u3 u4 u5 We consideris a ul u2 u3 u4 u5 rough fuzzy set on with p ч 1 1 °-4 л_ 11 and ul u2 u3 u4u5 -11111 F2 = aprD(F2) = — +—+ — + — +-p= U. 2 r RVul u2 tz3 u4 u5 A rough fuzzy relation on based on where "1 1 0 0 1" 1 1 0 0 1 1 1 0 0 — — 0 M (^F ) = F2 2 1 2 1 0 0 — — 0 2 2 Li 1 0 0 1J is clearly the - reflexive, symmetric rough fuzzy relation. We have M (^.р Г1 1 0 1 1 0 1 ^F ) = F2 0 0 — 2 1 0 0 — 2 L1 1 0 It is obvious that then is the transitive rough fuzzy relation; so that, is a - similarity relation. VIII. Conclusion In this paper, we have developed the rough fuzzy relation on two universe sets and studied some theoretical results of rough fuzzy relations. In the future, we will explore the information measures based on rough fuzzy relations and apply in the feature selection problems, as well as find the attribute reduction sets in the data table or build databases based on rough fuzzy relations.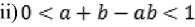
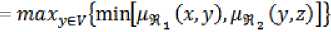
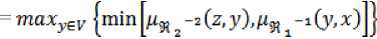
0
0
0
0.5
0
0.5
1
0
1
0
0
0
Ю.6
0
0.4
o-0
At U
A
B
C
D
u1
0.1
0.2
0.3
Y
u2
0.1
0.3
0.4
N
u3
0.2
0.3
0.5
Y
u4
0.2
0.3
0.5
Y
u5
0.6
0.4
0.3
N
is an equivalent relation on , is a crisp approximation space and
Список литературы Rough Fuzzy Relation on Two Universal Sets
- Z. Pawlak, Rough sets, International Journal of computer and information sciences 11(5), 341 - 356, 1982.
- T. Beaubouef, F. Petry, Normalization in rough relation database, International conference on rough sets, fuzzy sets, data mining and granular computing, pp 257-265, 2005.
- T. Beaubouef, F. Petry, Rough and rough fuzzy sets in design of information systems, Computational Complexity: theory, technique and application, pp 2702-2715, 2012.
- L.A. Zadeh, Fuzzy set, Information and control (8), pp 338-353, 1965.
- Y.Y.Yao, Combination of rough and fuzzy sets based on level sets, Rough sets and Data mining: analysis for imprecise data, Kluwer Academic Publisher, Boston, pp 301 – 321, 1997.
- A. Skowron, Rough – fuzzy computing, Handbook of natural computing, Springer – Verlarg Berlin Heidelberg, pp 1921 – 1948, 2012.
- W. Z. Wu, Y. H. Xu, On fuzzy topological structures of rough fuzzy sets, Transactions on rough sets XVI, LNCS 7736, Springer – Verlag Berlin Heidelberg, pp 125-143, 2013.
- S. Lan, Fuzzy rough relation and Its properties, Journal of Systems science and Systems Engineering, V. 11, N. 3, pp 367 – 370, 2002.
- T. K. Samanta, B. Sarkar, Fuzzy rough relation, G.J.P and A Sc and Tech, Vol 01, pp 10 – 17, 2011.
- W. B. V. Kandasamy and F. Smarandache, Fuzzy relational maps and neutrosophic relational maps, HEXIS Church Rock, 2004.


