Сценарные оценки потепления климата и смертности населения российских приарктических городов в ХХI в
Автор: Шапошников Д.А., Ревич Б.А., Школьник И.М.
Журнал: Анализ риска здоровью @journal-fcrisk
Рубрика: Анализ риска здоровью в гигиене
Статья в выпуске: 4 (28), 2019 года.
Бесплатный доступ
Изменения климата наиболее выражены в Арктическом регионе. Климатические прогнозы свидетельствуют о продолжающемся потеплении на циркумполярной территории. Поставлена задача определения атрибутивной доли смертности, обусловленной экспозицией к неоптимальным температурам воздуха в рамках указанных сценариев. Зависимость суточной смертности от среднесуточных температур воздуха получена в рамках нелинейной модели с распределенным лагом. Суточные температурные аномалии, ожидаемые к середине и концу ХХI в., вычислены по ансамблевым расчетам региональной климатической модели Главной геофизической обсерваторией им. Воейкова с использованием репрезентативных траекторий концентраций парниковых газов Межправительственной группы экспертов по изменению климата: RCP4.5, приводящий к умеренному потеплению, и RCP8.5, приводящий к максимальному потеплению. Потепление в российских приарктических городах будет сопровождаться повсеместным снижением температурно-зависимой компоненты смертности...
Изменение климата, потепление климата, климатические модели, смертность населения, арктика, болезни органов кровообращения, цереброваскулярные болезни, болезни органов дыхания
Короткий адрес: https://sciup.org/142223305
IDR: 142223305 | УДК: 614.1 | DOI: 10.21668/health.risk/2019.4.04
Текст научной статьи Сценарные оценки потепления климата и смертности населения российских приарктических городов в ХХI в
Климатические сценарии при всех их неопределенностях невозможны без конкретных численных предположений о траектории развития общества. Начиная с 2014 г. Межправительственная группа экспертов по изменению климата (МГЭИК) суммирует эти предположения в «репрезентативные траектории концентраций» парниковых газов, из которых в данной работе рассмотрены два сценария радиационного воздействия на климатическую систему: RCP 4.5 , приводящий к умеренному потеплению, и RCP 8.5 , приводящий к максимальному потеплению, при отсутствии мер по ограничению эмиссий парниковых газов [1, 2].
Разнообразные прямые и опосредованные пути воздействия изменений климата на здоровье населе- ния наиболее интенсивно изучаются на территориях, где изменение климата особенно заметно или имеет наибольшую амплитуду, в том числе в России. Средняя скорость роста среднегодовой температуры воздуха на территории Российской Федерации в 1976–2018 гг. составила 0,47 °С/10 лет при скорости роста глобальной температуры за тот же период: 0,17–0,18 °С/10 лет [3]. Поскольку территория нашей страны охватывает различные природноклиматические зоны, региональные различия в прогнозах потепления также велики. Можно ожидать и проявления различий в особенностях влияния изменения климата на смертность, как это было уже отмечено в других странах с большой территорией. Например, в Бразилии отмечено возрастание влия-
Ревич Борис Александрович – доктор медицинских наук, профессор, главный научный сотрудник, заведующий лабораторией прогнозирования качества окружающей среды и здоровья населения (e-mail: ; тел.: 8 (499) 129-18-00; ORCID: .
Школьник Игорь Маркович – кандидат физико-математических наук, ведущий научный сотрудник, заведующий отделом динамической метеорологии и климатологии (e-mail: ; тел.: 8 (812) 372-50-33; ORCID: .
ния потепления на смертность при движении от регионов с умеренным климатом к экваториальным, где прогнозируется наибольший прирост дополнительной смертности [4].
На российских арктических и приарктических территориях прогнозируется гораздо более быстрый рост приземных температур воздуха, чем в среднем по планетарной суше или по территории страны. Например, сравнение среднегодовых температурных аномалий за период 2000–2009 гг. по сравнению с 1951–1980 гг. показывает эффект «полярной амплификации»: аномалия в Арктике уже достигает 2 °С по сравнению с глобальной 0,6 °С [5]. Главные причины этого явления – по-видимому, изменение альбедо полярных шапок из-за таяния льдов и особенности высотных струйных течений в атмосфере [6].
Зарубежные территории с субарктическим климатом включают Северную половину Скандинавии, большую часть Аляски и часть Канады к северу от 50° с.ш. Согласно российскому законодательству, наиболее значимыми критериями зонирования при определении территорий Крайнего Севера (к ним относятся города Мурманск и Якутск) и приравненных к ним местностей (в том числе г. Архангельск) являются природно-климатические факторы, главным из которых является низкая температура воздуха. Всего на таких территориях сейчас проживает 8,2 млн человек, или около 5,8 % населения РФ. Естественно ожидать, что потепление может дать преимущества для всего этого населения, такие как уменьшение числа случаев смерти из-за смягчения суровости местного климата и рост сельскохозяйственного производства вследствие увеличения теплообеспеченности и продолжительности вегетационного периода1.
Цель работы – количественно оценить последствия изменения температурного режима приполярных территорий для прогнозируемой смертности проживающего там населения, проведя прямое доказательное эпидемиологическое исследование влияния температурного режима на смертность, которое возможно только для компактно проживающей популяции достаточного размера, отслеживаемой в течение достаточного периода времени. Это возможно только по городам с численностью более 100 тыс. населения [7, 8].
Материалы и методы. Постановка прогнозного исследования. В исследовании использованы условные прогнозы ожидаемых в Мурманске, Архангельске и Якутске изменений среднесуточных температур воздуха в XXI в., полученные по ансамблевым расчетам с региональной климатической моделью Главной геофизической обсерваторией им. А.И. Воейкова Росгидромета. Региональная климатическая модель имеет более высокое разрешение (25 км) по сравнению с глобальными моделями и поэтому лучше описывает мезомас-штабную изменчивость климата и ее вклад в неопределенность локальных оценок будущих изменений климата. В качестве базового периода климатического прогноза выбрана декада 1990–1999 гг., а для описания динамики ожидаемых изменений выбрано два прогнозных периода – середина (2050–2059 гг.) и конец текущего века (2090–2099 гг.). Таким образом, всего было изучено два сценария выбросов: RCP4.5, приводящий к умеренному потеплению, и RCP8.5, приводящий к максимальному потеплению, и два горизонта прогнозирования, для которых рассчитаны ожидаемые изменения смертности, вызванные изменением температурного режима во все календарные даты. В качестве входных данных при моделировании будущих изменений смертности использованы суточные температурные аномалии с соответствующим внутриан-самблевым стандартным отклонением. Размер ансамбля 25 членов для сценария RCP4.5 и 50 членов для сценария RCP8.5.
Показатели смертности. Анализ смертности проведен по «климатозависимым» причинам смерти. В каждом из трех городов изучено 10 показателей смертности: пять групп причин (все естественные причины, все болезни органов дыхания, все болезни системы кровообращения, среди которых отдельно инфаркты и инсульты) в двух возрастных группах (смерть в возрасте от 30 до 64 лет и от 65 лет). Пожилые лица старше 65 лет особенно чувствительны к изменениям температурного режима в результате потепления [9]. Общее количество изученных случаев в обеих возрастных группах приведено в табл. 1.
Температурная кривая смертности и атрибутивный риск . При разработке прогноза дополнительной смертности, связанной с температурой, была установлена зависимость ежедневной смертности от среднесуточных температур воздуха в базовом периоде и оптимальная температура, при которой ожидаемая смертность минимальна ( ММТ – minimum mortality temperature). Величина ММТ является важной характеристикой популяции, зависящей не только от местного климата, но и от особенностей проживающего там населения (в том числе этнических). В некоторых городах (например в Норильске) из-за значительной миграции населения невозможно определить эту величину.
Для численного описания влияния экспозиции населения к неоптимальной температуре использована мера относительного увеличения смертности – атрибутивная доля (AF – attributable fraction) и абсолютный прирост смертности (AN – attributable number). Обе величины являются мерами атрибу- тивного риска и были вычислены в данной работе, поскольку AF позволяет сравнивать различные города между собой, в то время как AN информирует об абсолютном количестве смертей в каждом городе (например за год). Меры атрибутивного риска определялись в референтный день i с температурой воздуха T относительно гипотетической ситуации, когда температура в этот день была бы равна MMT:
AF T = 1 – exp (–β T ); AN T = n AF T , (1) где β T есть «лог-риск» – логарифм относительного прироста смертности, обусловленного приростом температуры от ММТ до T , а n есть общая смертность в референтный день i , обозначим ее M i , экспозиции T . Это определение может быть обобщено для отсроченных зависимостей, как раз имеющих место в нашем случае, когда среднесуточная температура воздуха в любой заданный наперед «референтный» день повлияет на суточную смертность в данном городе в течение конечного периода продолжительностью L +1 день (единица здесь появляется потому, что лаг считается от нулевого – т.е. референтного дня). Это обобщение достигается рассмотрением вектора прошлых экспозиций T i …T i-L и соответственно «шлейфа» парциальных рисков в ( T i-i , l ), l G [0; L ], в совокупности характеризующих отсроченное влияние температуры на смертность в течение всего этого периода. Такое обобщение впервые было сделано работе [10] и был предложен метод вычисления значений атрибутивного риска. Таким образом, риск зависит от двух переменных – температуры и лагов, поэтому решением задачи является построение двумерной поверхности рисков в пространстве возможных значений температур и лагов. Поскольку речь здесь идет об острых эффектах для здоровья, максимальный лаг не превышает 2–3 недель.
Модель смертности с распределенным лагом . Для вычисления величин β ( T 0 ) … β ( T i ) использована нелинейная модель смертности с распределенным лагом [11]. Эта модель стала общепринятой в исследованиях отсроченных зависимостей смертности от метеорологических показателей и концентраций загрязняющих веществ. В качестве входных данных использованы данные Росстата о ежедневной смертности в каждом городе с разбивкой по причинам и возрастам за период 1999–2016 гг., а также метеорологические данные Всероссийского научно-исследовательского института гидрометеорологической информации о среднесуточных температурах воздуха за этот же период.
Обозначим временные ряды среднесуточной температуры и смертности за период моделирования температурно-зависимой компоненты смертности как векторы из 6576 (столько всего дней в периоде 1999–2016), упорядоченных во времени наблюдаемых значений среднесуточной температуры воздуха Tols и ежедневной смертности Ml. Первый вектор является «вектором экспозиции» а второй, соответственно, «ответом». Тогда зависимость смертности от температуры с учетом отсроченного и распределенного во времени характера воздействия задается двумерной поверхностью s в пространстве температур и лагов:
log [ E ( M l ) ] = а + s (To t ; 0 ) + f ( i ; в) + 1 ( dow ; y ). (2)
В уравнении (2) предполагается пуассоновская функция распределения ежедневной смертности, отсюда логарифмическая связующая функция, а остальные два слагаемых описывают явную зависимость смертности от времени – т.е. номера дня i и дня недели dow с соответствующими векторами регрессионных параметров в и у . Основополагающим при таком подходе является понятие о двумерном базисе, по которому раскладывается функция риска s . При двумерной параметризации параметр-вектор 0 представляет собой коэффициенты разложения функции s по этому базису – тензорному произведению двух одномерных базисов – в пространстве температуры и в пространстве лагов. Введение базисных функций нужно для уменьшения числа степеней свободы регрессионной модели смертности – произвольная зависимость раскладывается по конечному (и даже очень небольшому) набору базисных функций. В данном случае базис в пространстве температур воздуха представлял собой натуральный кубический сплайн с тремя внутренними узлами, соответствующими определенным процентилям исторического распределения среднесуточных температур в каждом городе (см. табл. 1), а именно Т 10 % , T 75 % и T 90 % . Асимметричный выбор узлов ( T 75 % вместо T 50 %) отражает фундаментальную асимметричность температурной зависимости смертности. Узлы кубического сплайна в пространстве лагов располагались в днях 1, 3, 9, т.е. было выбрано всего три внутренних узла с таким расчетом, чтобы они были приблизительно линейно расположены по логарифмической шкале времени c максимальным лагом L = 21 день. Это предположение означает, что начало этого периода содержит больше информации об отклике смертности, чем конец периода.
Таблица 1
Описание исходных данных для моделирования смертности. Значения минимальной, максимальной среднесуточных температур, положения внутренних узлов температурных сплайнов (°С), общее изученное количество случаев смерти от всех естественных причин за период 1999–2016 гг.
|
Параметр |
Город |
||
|
Мурманск |
Архангельск |
Якутск |
|
|
Т -min |
–38 |
–37 |
–51 |
|
T 10 % |
–10,9 |
–13,3 |
–37,9 |
|
T 75 % |
8,5 |
10,3 |
12,0 |
|
Т 90 % |
12,9 |
16,3 |
18,6 |
|
т max |
25 |
27 |
28 |
|
Количество изученных случаев смерти от всех естественных причин |
|||
|
Возраст, лет: 30–64 |
28 435 |
26 427 |
13 554 |
|
65 и старше |
33 137 |
44 213 |
14 597 |
Вычисление атрибутивных рисков . Модель (2) учитывает все дни периода исследования, а не только теплый или холодный периоды, поэтому такая модель позволяет получить оценочные значения смертности M i и атрибутивную смертность А— сразу для всех дней периода исследования. Просуммировав ANi , получается общая атрибутивная смертность ANtot , которую можно затем подразделить на два
слагаемых, соответствующих всем дням с температурой выше оптимальной и всем дням с температурой ниже оптимальной. Эти два слагаемых характеризуют влияние жары и холода и обозначаются AN heat
и AN cold . После этого, согласно определению (1), рассчитываются атрибутивные фракции для жары и холода:
———
—
AF cold =
AN cold
———
Mtot
—
AF
heat =
AN heat
Mtot
Такой расчет можно сделать для различных прогнозных сценариев среднесуточных температур в будущем Tf , используя одну и ту же модель смертности, задаваемую уравнением (2). С помощью этой модели определяют функцию «доза – ответ» (дозой является отклонение температуры от оптимальной, а ответом – относительное повышение смертности). Поскольку эта функция предполагается неизменной на протяжении всего XXI в., model в уравнении (4) для атрибутивной фракции в будущем AFf зависит только от наблюдаемых температур Tobs :
* * *
AFf = attrdl ( Tf , crossbasis , Mobs , model ( Tobs ...)). (4)
В уравнении (4) T f = Tobs +Δ T , Δ T есть вектор суточных температурных аномалий – периодическая функция с периодом один год (рис. 1) на протяжении прогнозной декады; «…» означают другие параметры модели (2); crossbasis означает двумерный базис, по которому разлагается поверхность рисков β ( Ti-l , l ), получаемый прямым (декартовым) произведением двух одномерных базисов в пространстве температур и лагов. Пользовательская функция attrdl.R для вычисления атрибутивных рисков в программной среде R была написана для R -пакета dlnm 2.2.0 и доступна в онлайн-приложении к работе [10].
Построение доверительных интервалов для мер атрибутивного риска . Поскольку относительная точность климатического прогноза при всех сценариях и горизонтах прогнозирования остается в несколько (в 5–6) раз выше, чем точность базовых оценок AF и AN , то итоговые доверительные интервалы прогнозных оценок можно приближенно вычислить в два шага. На первом шаге из заданного сценария выбросов формируются три температурных сценария, соответствующие центральной оценке, нижней и верхней границе доверительных интервалов прогнозируемых среднесуточных температур, и для каждого из этих температурных сценариев вычисляются атрибутив-
ные количества смертей AN и фракции AF . Обозначим эти фракции AFf ( T l.b . ), AFf ( T mean ), AFf ( T u.b . ). Здесь l.b . и u.b . означают нижнюю и верхнюю границы 95%-ного доверительного интервала (ДИ) прогнозируемых температур, T mean – центральную оценку для каждой календарной даты. Каждая атрибутивная фракция вычисляется со своими доверительными интервалами. На втором шаге конструируются итоговые доверительные интервалы AN и AF , учитывающие обе ошибки (климатической и эпидемиологической моделей). Нижняя граница итогового ДИ выбирается как минимум из трех нижних границ доверительных интервалов вокруг AFf ( T l.b . ), AFf ( T mean ), AFf ( T u.b. ). Аналогично, итоговая верхняя граница доверительного интервала AFf выбирается как максимум из трех верхних границ тех же доверительных интервалов. Это допущение является консервативным, поскольку оно комбинирует доверительные интервалы результатов двух независимых модельных расчетов, что ведет к незначительному преувеличению (уширению) итоговых доверительных интервалов. Малость уширения по сравнению с истинными доверительными интервалами вокруг прогнозных оценок AFf обеспечивается как раз большой разницей в неопределенностях климатической и эпидемиологической моделей.
Результаты и их обсуждение. В изученных городах повышение температуры прогнозируется во все месяцы года и почти линейно со временем, то есть к концу XXI в. температуры вырастут примерно в два раза больше, чем к середине века. Температурные аномалии имеют ярко выраженный сезонный характер. На рис. 1 показано максимальное потепление при наиболее агрессивном сценарии радиационного воздействия RCP 8.5 к концу века. Для облегчения сравнений между городами все три диаграммы на этом рисунке выполнены в едином масштабе. Порядок расположения городов в направлении от морского климата к континентальному соответствует росту зимних аномалий. Прогнозируемое потепление зимой в Мурманске меньше, чем в Архангельске: величина Т аномалии около +8 °С в Мурманске и более +9 °С в Архангельске. Летние температурные аномалии в этих двух городах примерно одинаковы: около +5 °С. В Якутске сезонность потепления выражена еще сильнее: при том же сценарии выбросов разница между зимними и летними температурными аномалиями уже примерно в четыре раза: потеплеет на 3 °С летом, а в ноябре и декабре на 12 °С. При «умеренном» сценарии радиационного воздействия RCP 4.5 амплитуда потепления будет примерно в два раза меньше. Обратите внимание на чрезвычайно узкие доверительные интервалы вокруг центральных оценок температурных аномалий. Например, в Архангельске для показанного на рисунке сценария относительная стандартная ошибка прогнозируемых температурных аномалий варьируется от 1,5 % в апреле до 3,5 % в середине лета и в середине зимы.
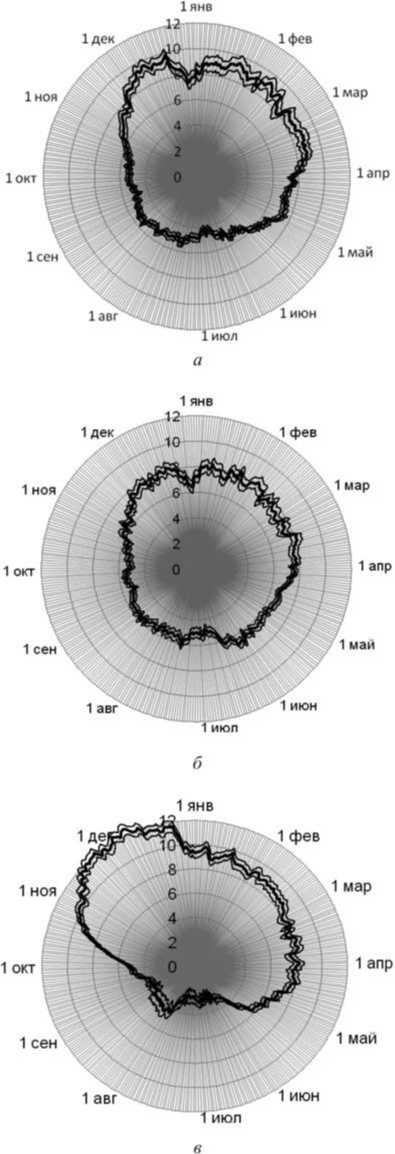
Рис. 1. Суточные температурные аномалии, прогноз на декаду 2090–2099 гг. по сравнению с периодом 1990–1999 гг., сценарий RCP 8.5. Толстая линия показывает среднюю оценку, тонкие линии – границы 95%-ного ДИ.
По вертикальной оси температура в °C: а – Архангельск; б – Мурманск; в – Якутск
Базовая линия температурно-зависимой смертности . Вычисление популяционной атрибутивной доли смертности и атрибутивного числа смертей проведено отдельно для всех дней со среднесуточными
температурами ниже оптимальной ( AF cold ) и выше оптимальной ( AFheat ) по формулам (3) для тех показателей смертности, для которых была установлена характерная U -образная зависимость смертности от температуры. Поскольку временной ряд ежедневной смертности Mobs представляет собой случайную функцию, установить эту зависимость возможно только при достаточной статистической мощности исходной выборки смертности. Например, ни в одном из трех городов не удалось установить этой зависимости для смертности от цереброваскулярных заболеваний (инсультов) в возрастной группе 30–64 лет из-за малого числа случаев. Естественно, на достоверность оценок AF влияет не только мощность выборки, но и чувствительность самого показателя смертности к изменению температуры, а также местный климат и особенности местного населения. Например, одна из особенностей Якутска – быстро растущая численность населения: за период исследования оно выросло со 195 тысяч в 1999 г. до 304 тысяч в 2016 г. Несмотря на сопоставимую численность населения Архангельска, Мурманска и Якутска (348, 316 и 250 тысяч на 2007 г. – середину периода базовой модели), в Якутске изученное количество смертей было более чем в два раза меньше (табл. 1). Вероятно, это стало причиной малого количества достоверных результатов оценки риска в этом городе. Из 10 изученных показателей смертности в Архангельске было получено 8 достоверных (на уровне 0,05) оценок AF (6 для холода и 2 для жары), в Мурманске – 4 (3 для холода и одна для жары); в Якутске – всего одна (для холода). Уже этот результат позволяет говорить о более сильном влиянии холода на смертность во всех городах, а также о сильном влиянии местных особенностей.
Сравнение абсолютных величин полученных в работе базовых оценок AFcold и AFheat наиболее информативно для тех показателей смертности, для которых обе оценки были статистически значимы. Это возможно лишь для двух показателей: смертности от инсультов и от всех БСК в Архангельске в возрастной группе 65+. Для первого из них AF cold = 0,240; AF heat = 0,010; т.е. значение AF cold превосходит AF heat в 24 раза, для второго AF cold = 0,236; AF heat = 0,007; т.е. значение AF cold превосходит AF heat в 34 раза. Такое различие в порядке величин заставляет предположить, что будущие изменения Δ AFcold по мере потепления также будут превосходить Δ AFheat по абсолютной величине. Вероятно, эти различия связаны как с механизмами отклика смертности населения на холод и жару, так и с фундаментальной асимметричностью температурной кривой смертности относительно среднегодовой температуры: ММТ соответствует примерно 90-му процентилю распределения среднесуточных температур. Таблица 2 содержит полученные значения ММТ как в °С, так и в терминах процентилей локальных многолетних распределений среднесуточных температур. Если сравнить температурную кривую смертности по форме с хок-
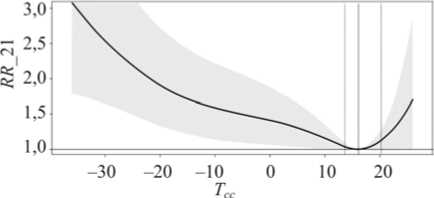
Рис. 2. Кумулятивный относительный риск смертности, накопленный в популяции в течение 21 дня (RR_21) после воздействия среднесуточной температуры воздуха Tcc (°C), полученной в Архангельске для смертности от инсультов в возрасте 65+. Сплошная вертикальная линия – ММТ (+16,1°C), вертикальные пунктирные линии – 95%-ный доверительный интервал, серый тон – доверительные интервалы относительного риска кейной клюшкой, то ее «черенок» будет длинней «крюка» примерно в 10 раз (рис. 2).
Из табл. 2 видно, что результаты оценки рисков в Архангельске надежнее, чем в других двух городах, потому что значения ММТ находятся в Архангельске в очень узком диапазоне – от 16,1° до 18,0 °С, исключая выпадающее значение, помеченное звездочкой. В Мурманске значения ММТ находятся в диапазоне от 12,4° до 17,7 °С, в Якутске – от 16,2° до 19,5 °С. По мере изменения климата от морского к континентальному абсолютные значения ММТ возрастают, а относительные, то есть вычисленные в терминах процентилей локальных распределений среднесуточных температур, наоборот, снижаются от 93-го процентиля в Мурманске до 88-го в Якутске. Снижение существенное, возможно, связанное с типом климата. Для сравнения укажем, что вычисленные нами по аналогичной методике оценочные значения ММТ в городе Ростове-на-Дону находились в диапазоне от 22,7° до 25,5 °С, то есть в более широком интервале, чем в Архангельске, со средним значением, соответствующему 89-му процентилю [12]. Средние значения в данном случае не являются наиболее вероятными, поскольку нет оснований предполагать, что значения ММТ для разных показателей смертности должны быть одинаковы в данном городе. Патофизиологические механизмы смертности от разных причин различны, поэтому указанные в табл. 2 оценочные значения взяты из разных распределений, а не из одного. Также отметим, что некоторые из исследованных распределений суточной смертности не являются статистически независимыми, потому что БСК складывается из ИБС и ЦВБ, а все естественные причины в свою очередь содержат примерно 2/3 БСК.
Прогнозируемая динамика климатозависимой смертности отдельно для тепла и холода . Атрибутивные фракции AF heat и AF cold изображены на рис. 3.
Для примера был взят показатель «Смертность от инфарктов в возрасте 65+», хотя похожие рисунки были получены и для остальных включенных в исследование показателей. Этот показатель выбран потому, что для него были получены оценки соответствующих фракций во всех трех городах, и при этом он показал во всех городах количественно сходные результаты в отношении поведения во время жары. На этом рисунке хорошо заметно, что холодозависимая смертность значительно превышает теплозависимую во всех городах и при всех сценариях потепления. Величина атрибутивной фракции AF heat растет при изменении климата от морского к континентальному: базовая оценка АFhbeat увеличилась от 0,2 % в Мурманске до 0,4 % в Архангельске и до 1,9 % в Якутске. При этом растут не только абсолютные величины AFheat , но и их изменения между декадами. Чтобы лучше понять характер этих изменений, прокомментируем, например,
Таблица 2
Температура, при которой смертность минимальна ( ММТ ), °С, и процентиль многолетнего распределения среднесуточных температур
|
о а Н со Ч О Щ |
Причина смерти |
Город |
|||||
|
Мурманск |
Архангельск |
Якутск |
|||||
|
°С |
процентиль |
°С |
процентиль |
°С |
процентиль |
||
|
40 |
ИБС |
– |
– |
17,1 |
92 |
25,0* |
99 |
|
ЦВЗ |
– |
– |
– |
– |
– |
– |
|
|
БСК |
– |
– |
18,0 |
93 |
– |
– |
|
|
БОД |
– |
– |
16,9 |
91 |
17,3 |
87 |
|
|
Естеств. |
12,4 |
89 |
17,1 |
92 |
– |
– |
|
|
+ 40 |
ИБС |
16,4 |
96 |
17,5 |
92 |
16,2 |
85 |
|
ЦВЗ |
– |
– |
16,1 |
90 |
– |
– |
|
|
БСК |
17,7 |
98 |
16,6 |
91 |
19,5 |
92 |
|
|
БОД |
12,8 |
90 |
11,3* |
77 |
17,8 |
88 |
|
|
Естеств. |
14,8 |
94 |
16,6 |
91 |
18,8 |
90 |
|
|
Среднее знач. |
14,8 |
93 |
17,0 |
91 |
17,9 |
88 |
|
П р и м е ч а н и е : * – выпадающие значения; средние вычислены без этих значений; ИБС – ишемическая болезнь сердца; ЦВЗ – цереброваскулярные заболевания; БСК – все болезни системы кровообращения; БОД – все болезни органов дыхания; естеств. – все естественные причины. Прочерк – значение не установлено.
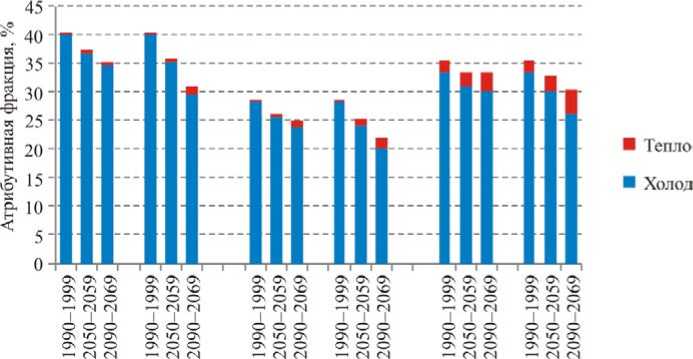
Рис. 3. Атрибутивные фракции (%) для показателя «Смертность от инфарктов в возрастной группе старше 65 лет» в результате воздействия температур воздуха выше оптимальной ( AFheat – красный цвет) и ниже оптимальной ( AFheat – синий цвет). Горизонтальная ось – декады для прогнозирования
последние три столбца, соответствующие сценарию RCP 8.5 в Якутске: на протяжении XXI в. AFheat увеличится с 1,9 до 4,3 %, то есть вырастет на 2,4 %. Одновременно AF cold снизится с 33,6 до 26,3 %, то есть уменьшится на 7,3 %. Видим, что для всех городов и сценариев выбросов уменьшение холодозависимой смертности более чем компенсирует увеличение теплозависимой смертности. Поэтому результирующий эффект оказывается благоприятным: суммарная доля AF tot монотонно снижается со временем. Подчеркнем, что процентные величины AF cold и AF heat специально сконструированы в определении (3) таким образом, чтобы их можно было суммировать непосредственно, потому что у них одинаковые знаменатели.
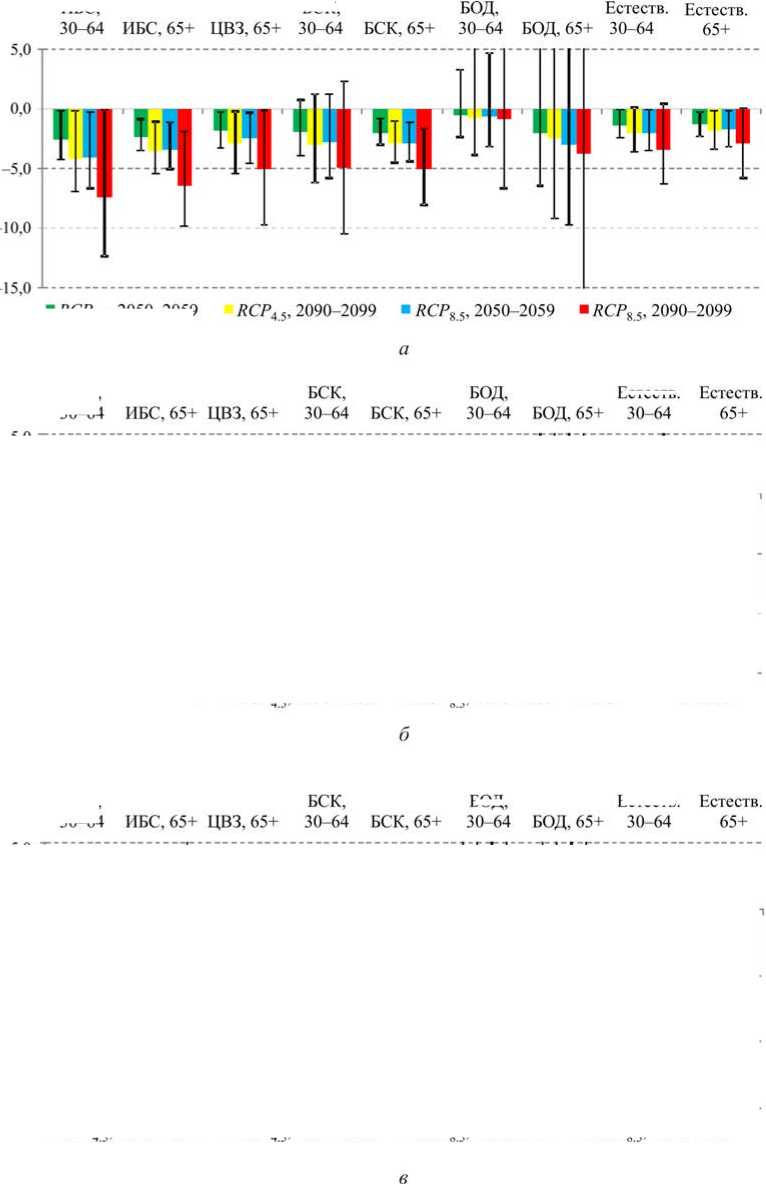
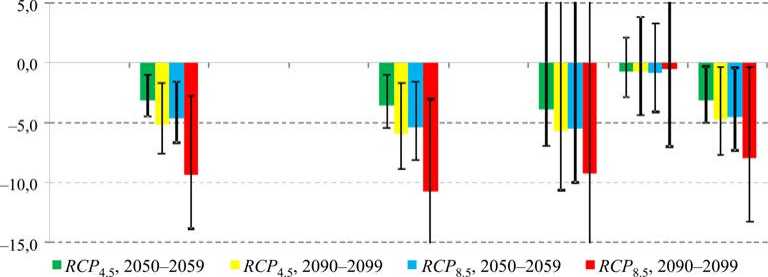
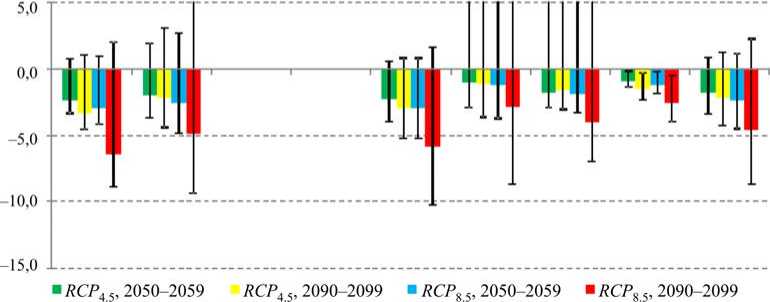
Результирующее влияние потепления на все изученные показатели смертности изображено на рис. 4. Обусловленные потеплением изменения со временем MP h^ = AF f at - AF b^ и A AF^ d = = AF cO^ — AF bd всегда будут разных знаков, поскольку холодозависимая смертность снижается, а теплозависимая смертность растет. Их арифметическая сумма дает итоговое изменение всей температурнозависимой смертности Δ AF tot между соответствующими декадами, которое выражено в процентах от общей смертности в данном городе согласно определению (3). Использование атрибутивных долей AF (в отличие от атрибутивных чисел AN ) удобно для сравнений между городами, регионами, странами и т.п. Для облегчения сравнений между городами все диаграммы на рис. 4 выполнены в едином масштабе по вертикальной оси.
Относительная стандартная ошибка ( RSE ) оценки AF cold значительно превосходит стандартную ошибку оценки AF heat , то есть при вычислении стандартной ошибки величины Δ AF tot можно вообще пренебречь ошибкой оценки AF heat и использовать следующее приближенное соотношение:
RSE (Δ AF tot ) ≈ RSE ( AF cold ). (5)
Это соотношение следует из того, что изменение фракции Δ AF Т линейно по лог-риску β T из уравнения (1) при β T << 1, что выполняется при всех температурах воздуха и остается справедливым до тех пор, пока относительная точность вычисления температурных аномалий (см. рис. 1) остается значительно выше относительной точности вычисления базовой оценки AF cold , о которой можно судить по доверительным интервалам относительных рисков на рис. 2. Приближенное равенство (5) позволило в изучаемой ситуации избежать эмпирического вычисления доверительных интервалов разностей Δ AF tot . Численное моделирование доверительных интервалов методом Монте-Карло обычно используется в таких задачах потому, что фракции AFb и AFf в уравнении (4) не являются статистически независимыми случайными величинами. При вычислении доверительных интервалов по формуле (5) была учтена их асимметричность: относительные ошибки параметра AF cold справа ( RSE+ ) и слева ( RSE– ) могут сильно различаться, и были использованы следующие соотношения:
RSE - ( AFmkl ) « ^—- b ; RSE + ( AF^ ) « ub^ . (6)
Данное заключение свидетельствует о необходимости отдельного вычисления положительной и отрицательной ошибок параметра Δ AF tot на рис. 4, при этом статистическая достоверность полученной оценки Δ AF tot определяется именно величиной RSE - ( AFcold ) : если на рис. 4 весь ДИ лежит целиком ниже оси абсцисс, то оценку Δ AF tot следует признать достоверной. Если же ДИ пересекает ось абсцисс, то нулевую гипотезу об отсутствии эффекта потепления на смертность нельзя отвергнуть.
ИБС,
БСК.
БОД.
Рис. 4. Изменения температурно-зависимой смертности по отношению к базовой линии 1990–1999 гг., прогнозируемые к середине XXI в. (декада 2050–2059) и концу века (декада 2090–2099). Величины Δ AFtot = Δ AFheat + Δ AFcold – результирующее влияние потепления в течение всей декады в процентах к суммарной смертности в базовом периоде согласно формуле (4). Вертикальные отрезки – 95%-ные доверительные интервалы прогнозируемых изменений.
Ось абсцисс – обозначения показателей смертности: ИБС – смертность от ишемической болезни сердца или инфарктов; ЦВЗ – смертность от цереброваскулярных заболеваний; БСК – смертность от всех болезней системы кровообращения; БОД – смертность от болезней органов дыхания; естеств. – смертность от всех причин, кроме внешних. Легенда указывает также на два сценария выбросов парниковых газов, приводящих к умеренному потеплению RCP 4.5 и максимальному потеплению RCP 8.5. Города расположены в направлении изменения типа климата от морского к континентальному: а – Архангельск; б – Мурманск; в – Якутск
КСРА5, 2050-2059
ИБС, 30-64
Естсств.
ИБС, 30-64
Естеств.
Сценарные различия . Для обоих сценариев потепления величина атрибутивной фракции AF tot продолжает снижаться со временем по сравнению с базовым периодом в течение всего XXI в., за одним исключением: это вся естественная смертность населения в возрасте 30–64 лет в Мурманске в сценарии RCP 8.5 . Для этого показателя к середине века Δ AF tot = –0,9 % [–4,1; 3,3 %], а к концу века Δ AF tot = –0,5 % [–7,0; 8,0 %]. Скорость увеличения аномалий смертности в точности равна скорости роста температурных аномалий для обоих сценариев потепления. Поясним это утверждение. По сценарию RCP 4.5 среднегодовая температурная аномалия достигнет в Мурманске Δ T = 2,4 °С к 2050–2059 гг. и Δ T = 3,7 °С к 2090–2099 гг. по сравнению с базовым периодом. Разделив Δ T 2090–2095 на Δ T 2050–2055 , получим 1,53. В Архангельске соответствующая величина равна 1,59, в Якутске 1,36, а в среднем для трех городов 1,49. Эту величину можно условно назвать средней скоростью (при)роста температурных аномалий за период между серединой и концом XXI в. Аналогично можно вычислить и скорость увеличения аномалии AF tot , разделив Δ AF 2090–2095 на Δ AF 2050–2055 . Например, для показателя «Смертность от ИБС в возрасте 65+ в Мурманске» это (–5,2 %)/(–3,1 %) = 1,68. Величины Δ AF tot отрицательные, изменения смертности увеличиваются со временем по модулю. Такой расчет был сделан для всех показателей смертности во всех трех городах, и затем была получена средняя оценка и дисперсия. Из расчета были исключены болезни органов дыхания во всех городах и вся естественная смертность населения в возрасте 30–64 лет в Мурманске по причине слишком широких доверительных интервалов полученных для них оценок Δ AF . Всего в расчете участвует 15 показателей: три в Мурманске, семь в Архангельске, пять в Якутске. В результате скорость прироста аномалий AF tot в сценарии RCP 4.5 за период между серединой и концом XXI века составила 1,47 ± 0,17, что практически совпадает со скоростью прироста температурных аномалий. Обратите внимание на очень узкое стандартное отклонение этой оценки. Для сценария RCP 8.5 соответствующие приросты равны 1,89 для температурной аномалии и 1,91 ± 0,15 для аномалии AF tot , то есть скорости роста опять совпадают. Этот результат важен потому, что никакого «перелома» тенденции снижения смертности к концу века не предвидится: годовая смертность снижается пропорционально росту температуры во всех сценариях выбросов.
Возрастные различия видны в числе установленных эффектов потепления на рис. 4. Хотя дизайн исследования предусматривал изучение равного количества показателей смертности в обеих возрастных группах, количество полученных результатов оказалось больше в старшей возрастной группе во всех городах (особенно это заметно в Мурманске). Эффект потепления можно оценить как изменение фракции ΔAFtot лишь для тех показателей смертно- сти, для которых установлена зависимость от температуры воздуха (см. рис. 2). Вероятно, невозможность установления такой зависимости (при достаточной статистической мощности выборки) должна быть связана с нечувствительностью данного показателя к изменению температуры воздуха. Если в данном городе и для данной причины смерти получены оценки эффекта потепления одновременно в двух возрастных группах, то можно ожидать, что эффект в старшей возрастной группе должен быть больше по абсолютной величине, чем в средней. Такие парные сравнения можно сделать в Мурманске лишь для одной причины – смертности от всех причин, кроме внешних, в Архангельске для всех причин, кроме инсультов, в Якутске для инфарктов, болезней органов дыхания и всех причин, кроме внешних. Всего набирается восемь пар, из которых в пяти случаях эффект больше в старшей возрастной группе и в остальных трех случаях (ИБС в Архангельске и Якутске, все причины, кроме внешних, в Архангельске) эффект больше в средней возрастной группе.
Географические различия в величине установленных эффектов потепления в контексте исследования наиболее интересны. Лишь для пяти из десяти исследованных показателей смертности эффекты потепления были установлены одновременно во всех трех городах. Один из этих пяти показателей (смертность населения от всех причин, кроме внешних, в возрасте 30–64 лет) показал выпадающие значения Δ AF tot в Мурманске (рис. 4) и поэтому был исключен из анализа, а оставшиеся четыре показателя приведены в табл. 3.
В Мурманске эффект потепления примерно в два раза больше по абсолютной величине, чем в остальных двух городах. В Архангельске и Якутске эффекты сравнимы по величине, причем в Якутске эффект, как правило, сильнее (для всех показателей кроме смертности от ИБС в возрасте 65+).
Атрибутивные числа смертей могут быть важны в некоторых ситуациях, например, когда необходимо посчитать экономическую оценку последствий потепления или принять определенные управленческие решения. В табл. 4 приведены оценки величин AN tot в динамике при различных сценариях выбросов, но лишь для всех причин, кроме внешних, поскольку этот показатель является интегральным.
Большинство результатов в табл. 4 статистически значимы, хотя доверительные интервалы достаточно широки. Величина ошибки определяется главным образом неопределенностью нисходящего (т.е. обусловленного воздействием холода) участка температурной кривой смертности (см. изображенные на рис. 2 доверительные интервалы). В абсолютных значениях смертность может снижаться по сравнению с базовым уровнем всего на несколько десятков человек в год. Например, в Якутске по сценарию сильного радиационного воздействия RCP 8.5 к концу века смертность может снизиться на 56 человек в год в сумме для двух возрастных групп.
Таблица 3
Изменения атрибутивных фракций температурно-зависимой смертности AFtot в процентах к базовому уровню: выбранные для анализа географических различий показатели
|
Показатель смертности |
Сценарии и горизонты прогнозирования |
RCP 4.5 , 2050–2059 |
RCP 4.5 , 2090–2099 |
RCP 8.5 , 2050–2059 |
RCP 8.5 , 2090–2099 |
|
ИБС, 65+ |
Мурманск |
–3,1 |
–5,2 |
–4,6 |
–9,4 |
|
Архангельск |
–2,4 |
–3,6 |
–3,4 |
–6,5 |
|
|
Якутск |
–2,0 |
–2,2 |
–2,6 |
–4,9 |
|
|
БСК, 65+ |
Мурманск |
–3,6 |
–5,9 |
–5,4 |
–10,8 |
|
Архангельск |
–2,0 |
–2,9 |
–2,9 |
–5,1 |
|
|
Якутск |
–2,3 |
–3,0 |
–3,0 |
–5,9 |
|
|
Все причины, кроме внешних, 65+ |
Мурманск |
–3,1 |
–4,7 |
–4,5 |
–8,0 |
|
Архангельск |
–1,3 |
–1,8 |
–1,7 |
–2,9 |
|
|
Якутск |
–1,8 |
–2,2 |
–2,4 |
–4,6 |
|
|
БОД, 65+ |
Мурманск |
–3,9 |
–5,7 |
–5,5 |
–9,2 |
|
Архангельск |
–2,0 |
–2,5 |
–3,0 |
–3,8 |
|
|
Якутск |
–1,8 |
–1,6 |
–1,9 |
–4,0 |
Таблица 4
Приведенные к одному году значения атрибутивных чисел смертности от всех естественных причин, суммарно для тепла и холода ( AN tot ), число случаев
|
Город |
Возраст, лет |
Базовый 1 |
RCP 4.5 |
RCP 8.5 |
||
|
1990–1999 |
2050–2055 |
2090–2095 |
2050–2055 |
2090–2095 |
||
|
Мурманск |
30–64 |
221 (–98; 424) |
213 (–80; 408) |
214 (–49; 408) |
211 (–41; 403) |
221 (–22; 392) |
|
65+ |
434* (53; 680) |
378* (11; 642) |
348* (21; 578) |
352* (25; 590) |
287* (4; 501) |
|
|
Архангельск |
30–64 |
265* (71; 423) |
245* (56; 387) |
235* (64; 382) |
236* (62; 370) |
214* (73; 343) |
|
65+ |
373* (104; 582) |
343* (93; 555) |
330* (76; 528) |
330* (77; 524) |
302* (87; 481) |
|
|
Якутск |
30–64 |
323* (29; 494) |
317* (19; 475) |
313* (0; 476) |
315* (0; 478) |
304* (8; 460) |
|
65+ |
198 (–74; 348) |
183 (–97; 346) |
179 (–79; 335) |
179 (–113; 331) |
161 (–113; 305) |
|
П р и м е ч а н и е: * – статистически значимая на 95%-ном уровне оценка.
Предыдущие прогностические оценки температуры к 2090–2099 гг. по сравнению с 2010–2019 гг. [13] по сценарию RCP 8.5 показывают сравнительно широкие доверительные интервалы вокруг средневзвешенных оценок среднегодовых температурных аномалий: для Северной Америки 4,9 °С (3,2–6,3) и для Северной Европы 3,4 °С (2,8–5,4) [13] (табл. 2). Северная Америка ближе по климату к приарктической зоне, чем Северная Европа, поскольку обладает континентальным климатом. Относительная стандартная ошибка прогноза довольно велика и составила, соответственно, 16 % и 19 %. Доверительный интервал для прогнозов температурных аномалий, использованных в данной работе, существенно уже: для того же сценария выбросов и тех же временных горизонтов среднегодовые температурные аномалии составили в Мурманске 5,4 °С (95%-ный ДИ 5,0–5,7 °С), в Архангельске 5,6 °С (5,2–,0 °С) и в Якутске 5,7 °С (5,3–6,1 °С), т.е. RSE около 3 %. Отметим хорошее согласование наших центральных оценок с величиной температурной аномалии 4,9 °С для Северной Америки.
При прогнозировании будущих изменений смертности предполагалось, что меняется только климат, сама же температурная зависимость смертности остается на протяжении XXI в. такой же, как в базовом периоде климатического прогноза. Это предположение означает отсутствие акклиматизации, индивидуальной и популяционной адаптации к климатическим изменениям. В действительности исследования длинных временных рядов смертности (на протяжении всего XX в.) показывают, что население само адаптируется к наблюдавшемуся в XX в. изменению климата. Так, значение ММТ в Стокгольме сдвигалось вправо по мере потепления как в абсолютном выражении (в °C), так и в относительном (как процентиль распределения среднесуточных значений температуры в день смерти). Процентиль вычислялся за 30-летние периоды с 1901 по 2009 г. За этот период абсолютные значения ММТ увеличились примерно с 11 до 20 °С, а относительные примерно с 70-го до 93-го процентиля [14]. При этом среднегодовые температуры увеличились всего на 1,4 °С. Аналогичный результат (о постепенном увеличении ММТ с течением времени) был получен во Франции с использованием данных о ежедневной смертности с 1968 г. [15]. В России такие работы не проводились, а оцифрованные данные о ежедневной смертности доступны лишь с 1999 г. Учитывая эти результаты, предположение об отсутствии адаптации, принятое в данной работе, может привести к преувеличению эффекта в будущем. Точнее, можно рассчитать лишь верхнюю границу искомого эффекта – максимальное (по абсолютной величине)
изменение температурно-зависимой смертности в результате ожидаемого потепления. Поэтому интерпретировать результаты данного исследования лучше не как прогноз изменения климатозависимой компоненты смертности с учетом всех имеющихся научных данных, а как сценарий возможных последствий изменения климата без учета адаптации населения.
Выводы. Потепление климата в Мурманске, Архангельске и Якутске приведет к снижению температурно-зависимой смертности, что подтверждают как результаты наших предыдущих исследований [16], так и глобального исследования [13]. Смертность от всех естественных причин в возрасте от 30 лет к 2090–2099 гг. по сравнению с 1990–1999 гг. в сценарии сильного радиационного воздействия RCP8.5 снизится в Мурманске на 4,5 % (95%-ный ДИ 1,1–7,9 %), в Архангельске – на 3,1 % (1,1–5,1 %) и в Якутске – на 3,6 % (0,3–7,0 %). Аналогичное изменение смертности по сценарию RCP8.5 ожидается к концу века и в Северной Европе –0,6 % (95%-ный ДИ –2,3–1,6 %) [14]. Тем не менее во время волн жары в приарктических городах смертность населения, особенно пожилого, будет возрастать [8, 17, 18]. Математические методы оценки воздействия таких волн на показатели смертности населения описаны в статье Д.А. Шапошникова и Б.А. Ревича [19].
Ожидаемое относительное снижение смертности в приарктическом регионе может быть в несколько раз более значительным, чем в Северной Европе, при этом доверительные интервалы полученных оценок близки по величине. Эти исследования дополняют друг друга, свидетельствуя о неравномерном распределении выгод и рисков, обусловленных глобальным потеплением. Несомненно, что сценарные оценки положительных и отрицательных последствий изменений климата в различных климатических зонах России необходимо включать в региональные планы адаптации, которые должны будут разрабатываться исполнительной властью. При этом важно использование и экономических показателей потерь здоровья, например, как это было сделано при оценке последствий аномальной московской жары 2010 г. [20].
Финансирование. Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-00-00600 (18-00-00596 и 18-00-00599).
Список литературы Сценарные оценки потепления климата и смертности населения российских приарктических городов в ХХI в
- Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change / R.K. Pachauri, M.R. Allen, V.R. Barros, J. Broome, W. Cramer, R. Christ, J.A. Church, L. Clarke [et al.] // R.K. Pachauri, L. Meyer eds. - Geneva, Switzerland: IPCC, 2014. - 151 p.
- The representative concentration pathways: an overview / D.P. Van Vuuren, J.A. Edmonds, M. Kainuma, K. Riahi, A.M. Thomson, K. Hibbard, G.C. Hurtt, T. Kram [et al.] // Climatic Change. - 2011. - № 109. - P. 5-31. DOI: 10.1007/s10584-011-0148-z
- Изменения климата 2018 год (декабрь 2017 - ноябрь 2018). Обзор состояния и тенденций изменения климата России. - М.: Институт Глобального климата и экологии имени академика Ю.А. Израэля Росгидромета, 2019. - C. 11.
- Temperature-related mortality impacts under and beyond Paris Agreement climate change scenarios / A.M. Vicedo-Cabrera, Y. Guo, F. Sera, V. Huber, C.F. Schleussner, D. Mitchell, S. Tong, E. Lavigne [et al.] // Climatic Change. - 2018. - Vol. 150, № 3-4. - P. 391-402. DOI: 10.1007/s10584-018-2274-3
- Temperatures are warming faster in the Arctic than anywhere else in the world. Here's why [Электронный ресурс]. - NASA. Earth Observatory, 2013. - URL: https://earthobservatory.nasa.gov/images/81214/arctic-amplification (дата обращения: 03.11.2019).
- Serreze M., Barry R. Processes and impacts of Arctic amplification: A research synthesis // Global and Planetary Change. - 2011. - Vol. 77, № 1-2. - P. 85-96. 10.1016 / j.gloplacha.2011.03.004
- DOI: 10.1016/j.gloplacha.2011.03.004
- Shaposhnikov D., Revich B. Toward meta-analysis of impacts of heat and cold waves on mortality in Russian North // Urban Climate. - 2016. - № 15. - P. 16-24.
- DOI: 10.1016/j.uclim.2015.11.007
- Shkolnik I.M., Efimov S.V. Cyclonic activity in high latitudes as simulated by a regional atmospheric climate model: added value and uncertainties // Environ. Res. Letters. - 2013. - Vol. 8, № 4. - P. 5007.
- DOI: 10.1088/1748-9326/8/4/045007
- The 2019 report of The Lancet Countdown on health and climate change: ensuring that the health of a child born today is not defined by a changing climate / N. Watts, M. Amann, N. Arnell, S. Ayeb-Karlsson, K. Belesova, M. Boykoff, P. Byass, W. Cai [et al.] // Lancet. - 2019. - Vol. 394, № 10211. - P. 1836-1978. 10.1016/S0140-6736 (19) 32596-6
- DOI: 10.1016/S0140-6736(19)32596-6
- Gasparrini A., Leone M. Attributable risk from distributed lag models // BMC Medical Research Methodology. - 2014. - Vol. 14, № 1. - P. 55.
- DOI: 10.1186/1471-2288-14-55
- Gasparrini A., Armstrong B., Kenward M.G. Distributed lag non-linear models // Statistics in Medicine. - 2010. - Vol. 29, № 21. - P. 2224-2234.
- DOI: 10.1002/sim.3940
- Температура воздуха и смертность: исследование пороговых значений жары и чувствительности населения на примере г. Ростов-на-Дону / Н.В. Шартова, Д.А. Шапошников, П.И. Константинов, Б.А. Ревич // Фундаментальная и прикладная климатология. - 2019. - № 2. - С. 66-94.
- Projections of temperature-related excess mortality under climate change scenarios / A. Gasparrini, Y. Guo, F. Sera, A.M. Vicedo-Cabrera // The Lancet Planetary Health. - 2017. - Vol. 1, № 9. - P. e360-e367. 10.1016/S2542-5196 (17) 30156-0
- DOI: 10.1016/S2542-5196(17)30156-0
- Evolution of minimum mortality temperature in Stockholm, Sweden, 1901-2009 / Å.D. Oudin, A. Tornevi, K.L. Ebi, J. Rocklöv, B. Forsberg // Environ Health Perspect. - 2016. - № 124. - P. 740-744.
- DOI: 10.1289/ehp.1509692
- Todd N., Valleron A.J. Space-time covariation of mortality with temperature: a systematic study of deaths in France, 1968-2009 // Environ Health Perspect. - 2015. - Vol. 123, № 7. - P. 659-664.
- DOI: 10.1289/ehp.1307771
- Climate change may reduce annual temperature-dependent mortality in subarctic: a case study of Archangelsk, Russian Federation / D. Shaposhnikov, B. Revich, V. Meleshko, V. Govorkova, T. Pavlova // Environ. Nat. Resour. Res. - 2011. - № 1. - P. 75-91.
- DOI: 10.5539/enrr.v1n1p75
- Влияние температуры воздуха на смертность населения Архангельска в 1999-2008 гг. / Ж.Л. Варакина, Е.Д. Юрасова, Б.А. Ревич, Д.А. Шапошников, А.М. Вязьмин // Экология человека. - 2011. - № 6. - C. 28-36.
- Impact of Temperature Waves on the Health of Residents in cities of the Northwestern Regions of Russia / B.A. Revich, D.A. Shaposhnikov, O.A. Anisimov, M.A. Belolutskaya // Studies on Russian Economic Development. - 2019. - Vol. 30, № 3. - P. 327-333.
- DOI: 10.1134/S1075700719030158
- Шапошников Д.А., Ревич Б.А. О некоторых подходах к вычислению рисков температурных волн для здоровья // Анализ риска здоровью. - 2018. - № 1. - С. 22-31.
- DOI: 10.21668/health.risk/2018.1.03
- Порфирьев Б.Н. Экономическая оценка людских потерь в результате чрезвычайных ситуаций // Вопросы экономики. - 2013. - № 1. - С. 46-68.
- DOI: 10.32609/0042-8736-2013-1-48-68


