Сдвиговое течение нелинейной упруговязкой жидкости

Известно, что не каждое решение уравнений движения фактически реализуется в природе. Реально существующие типы движений демонстрируют устойчивость к малым возмущениям. Полученные профили скорости должны быть динамически и кинематически допустимыми, т.е. удовлетворять не только гидродинамическим уравнениям, но и законам термодинамики, условиям на границах и лежать в пределах рассматриваемой геометрической зоны.

При исследовании работоспособности различных реологических моделей часто используют куэттовский тип течения, в котором кинематика потока известна заранее, а эффективная вязкость, а также первая и вторая разности нормальных напряжений подлежат определению. Многие линейные и нелинейные модели описывают такие течения вполне реалистично. Исследования, выполненные Трус-делом и Нолом [1], Колеманом [2], Данном и Фосдиком [3], показали, что существуют кинематически допустимые течения, в которых мощность напряжения может становиться отрицательной. Едва ли вероятно, что такие движения могут реализовываться в природе.

Изучение течения вокруг тела, проведенное Альтманом и Денном [4] для линейной упруговязкой жидкости Максвелла, привело авторов к заключению, что условие El2 = VRe We = 1 разграничивает две различные ситуации. В докритическом случае (El2 < 1) уравнения, описывающие течение, относятся к эллиптическому типу и имеют гладкие непрерывные решения. В закритиче-ском случае (El2 > 1) уравнения гиперболичны и их решения имеют сильные тангенциальные разрывы. Анализ некоторых нелинейных реологических моделей показал, что краевая задача о плоскопараллельном течении в канале под действием перепада давления может иметь неединственное решение и приводить к слабым тангенциальным разрывам в профиле скорости. Так, исследование течения четырехконстантной жидкости Олдройда в трубе [5] показало возможность неединственности решения задачи и немонотонности распределения градиента скорости в радиальном направлении. В зависимости от значений перепада давления и отношения времени ретардации к времени релаксации вычисленные профили скорости либо имеют гладкую параболическую форму, либо содержат слабые тангенциальные разрывы. Кривые течения такой жидкости имеют гистерезисный харак- тер. В работах [6, 7] рассмотрены одномерные течения раствора полимера в плоском канале под действием градиента давления. Для описания реологических свойств раствора полимера выбраны две модели. Первая является обобщением феноменологической модели Джеффриса [4] и содержит объективную временную производную с шестью произвольными материальными константами. Вторая - дифференциальная векторная модель, предложенная Рем-мелгасом, Харрисоном и Лилом, является аппроксимацией статистической модели Дои -Эдвардса - Марручи - Грызутти [4].

Для этих двух моделей получены точные аналитические решения задачи течения в плоском канале. Показано, что в обоих случаях, в зависимости от исходных параметров модели, задача может иметь как единственное, так и неединственное решение. Профили скорости могут быть либо гладкими, почти параболическими, либо содержать слабые тангенциальные разрывы. Найдены критериальные условия появления неоднозначных режимов течения.

В работах В.Н.Покровского, Г.В.Пыш-нограя и др. [8–11] предложено обобщение реологической модели Виноградова - Покровского. В диссертации С.А.Зинович "Полидисперсность в мезоскопической теории вязкоупругости линейных полимеров" (2001) приведено решение задачи о стационарном течении простого сдвига для модели Виноградова -Покровского методом последовательных приближений. Показано качественное соответствие зависимостей компонент тензора анизотропии от сдвига поведению вязкоупругой жидкости.

В работе [12] исследовано течение между параллельными плоскостями под действием постоянного перепада давления нелинейной вязкоупругой жидкости с одним тензорным внутренним параметром. Получены все точные аналитические решения этой задачи в параметрическом виде. Из множества решений выделены заведомо физически недопустимые решения. Получены распределения компонент тензора анизотропии, скорости и градиента скорости по высоте канала для различных параметров реологической модели. Показано, что для значений перепада давления выше критических наблюдается неоднозначность решения, приводящая к разрывам в профилях компонент тензора анизотропии.

Целью данной работы является получение и анализ всех аналитических решений задачи течения в плоском канале с подвижной границей нелинейной упруговязкой жидкости Виноградова - Покровского.

• 2.    Система реологических уравнений

Модифицированная модель Покровского–Виноградова получена при рассмотрении динамики невзаимодействующих гантелей, движущихся в нелинейной анизотропной среде. Гантель состоит из двух бусинок, соединенных пружиной. Форма и ориентация гантелей в потоке характеризуется тензором:

< РР >  1

a =------

< Р ²> 0   3

где р - вектор соединяющий концы гантели и описывающий относительное движение бусинок, < р2 >0 - равновесное значение выражения < р12 > + < р2 > + < р32 > . В равновесии a = 0 . Выражение для тензора напряжения и эволюционное уравнение для тензора анизотропии а имеют следующий вид:

о = - pI + 3—a,

^Т 0

V 1 + (к - в) I    2

a +--— a =—D - 3—a • a,

T0           3

где к ив - феноменологические пара- метры модели, которые характеризуют вклады, связанные с анизотропией, причем в учитывает вклад, связанный с ориентацией макромолекулярного клубка, к с его размерами; ц0 и г0 - начальные значения сдвиговой вязкости и времени релаксации;

V a - верхняя конвективная производная тензора анизотропии; I = au - первый инвариант тензора анизотропии.

• 3.    Сдвиговое течение в плоском канале

Для задачи стационарного течения простого сдвига уравнение неразрывности выполняется тождественно. Уравнение сохранения импульса преобразуется к виду дет     п да xy _ ^ '/0    xy _ g

дУ     Т0 дУ

£% = з n, ^s=£=о ду    т dу   ду

Система уравнений модели Виноградова – Покровского записывается следующим образом:

- 2Wa + a | 1 ^{+ ( к} -. ) | a^ + a, Ц    (5)

+3в I a2 + a2 1 = 0, xx     xy

^axy ( 1 ⁺ ( ^{К +} 2 ^в ) ^{( a}xx ^{+ a}yy )) = ^Wi ( ^ayy ^{+ 1 / 3} ) , ^{(6) a}yy f ^{1 +} ( ^К - ^в ) [ ^axx ^{+ a}yy )] ^{+ 3 в (} ^ y ^{+ a} .2 y ) = ^{0 (7)}

В результате получили зависимость компоненты тензора анизотропии a от Wi . Уравнение (14) является полиномом четвёртой степени относительно a a4y + A1 a№ + B1 af y + C1 ayy + D1 = 0.

Это уравнение может иметь два или четыре действительных корня и может не иметь действительных корней вообще в зависимости от знака дискриминанта Q ( к , в , Wi ) и знаков коэффициента a^ и выражения a 2 - 4 c .

а- = — a ,

‘j     Wi j

Q = 16 a4 c - 4 a3 b}2 - 27 b}4 +

^{1   1        1   1          1}                (15)

+144 ab2 c -128 a2 c2 + 256 c3,

где а - безразмерные компоненты тензора экстранапряжения (размерное значение определяется из a j = %а ); a_tJ - компоненты безразмерного тензора анизотропии a , в , к – безразмерные параметры модели, характеризующие вклад анизотропии, число Вайсен-берга Wi = т_оу •

где

aj = Bj

b =—

3.1. Исследование зависимости a_yy ( Wi )

Из уравнения (5) вычтем уравнение (7):

^{2 Wia}xy ^{- ( a}xx - ^ayy )| 1 ⁺ ( ^К + 2 ^в ) ^{( a}xx + ^ayy )) = 0 . ⁽⁹⁾

Подставим полученное соотношение (9) в (6):

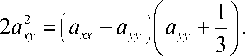
Выражение (10) для a ² подставим в уравнение (7) и выразим из него компоненту

a

xx

а : xx

Тогда

a yy ( в - 2 - (2 к + в ) a yy

в + (2к + в) ayy

а xx

a - a xx     yy

+ а      2 ayy (в - 1)

^yy в + (2 к + в ) a yy ’

₌ -2 a yy ( 1 + (2 к + в ) a yy j в + (2 к + в ) a yy

.

Подставим соотношение (13) в (10), а (12) в (6) и возведём в квадрат. Затем приравняем полученные выражения для a ² . xy

^{Wi 2 ( a} yy ^{+ 1}

в + (2 к + в ) a_№ j +

^J            (14)

+ a yy в ² ( 1 + (2 к + в ) a yy j ( 1 + a yy ( 2 к + 4 в - 3 ) ) 2 = 0 .

3 A ²

8    ,

A1 B1

3 A ⁴ A ² B A C

c = D,--- + ——1 —1—1

11256  16   4

Если Q <  0, то исследуемый полином четвертой степени будет иметь два действительных и два сопряженных мнимых корня. Если Q >  0, a_{ <  0 и a 2 - 4 c >  0, то полином будет иметь четыре действительных корня, в противном случае все корни уравнения четвертой степени будут мнимыми.

Характерный вид кривой Q = 0 представлен на рис. 1. В области I Q <  0, следовательно, существует два действительных корня уравнения (14), в области II Q >  0, a₁ <  0 и a 2 - 4 c >  0 и здесь существует четыре действительных решения рассматриваемого уравнения, в области III уравнение (14) не имеет действительных решений.

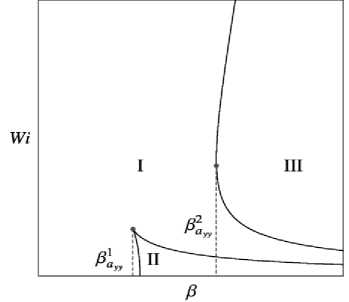
Рис. 1. Характерный вид кривой Q = 0

Поскольку дискриминант Q является

кубическим уравнением относительно Wi2 , то значения параметров в и в , при которых ayy         ayy происходит переход из области с двумя действительными решениями I в область с четырьмя решениями II , а также из области с двумя решениями I в область с чисто мнимыми решениями III , можно определить

Как видно из рис. 2, для а > 1 при в1 < в < в2 , т.е. когда решение проходит ayy              ayy через область II , нижняя кривая зависимости ayy (Wi) имеет S-образный вид (кривые 2, 3 для а = 1.5 на рис. 2). Для а <1 в этом диапазоне значений параметра в S-образный вид

аналитически:

ва,

284 + 886а + 918а2 + 421а3 + 80а4

---— --“—;—  +

4 ( 2 + а ) 2 [ 11 + 32 а + 23 а ² + 6 а ³)

3а — 3^(а + а — 2) [3 + 2а + а [

4(2 + а)2[11 + 32а + 23а2 + 6а3] ’

К

1,

J + 2а ’

а > 1

а < 1’

где для удобства введено обозначение

а = в

К

.

Например, для  а = 0.5,  в, ~ 1.172, ayy

в2 = 1.5, а для а = 1.5, ва “ 0.842, Д2 = 1.

ayy                                        ayy                    ayy

Характерный вид соотношения (14) для а >  1 и а <  1 представлен на рис. 2.

а = 0 . 5: в = 1)0 . 8 ; 2)1 . 12 ; 3)1 . 3 ; 4)1 . 51 .

зависимости a ( Wi ) появляется на верхней кривой (кривая 3 для а = 0 . 5 на рис. 2).

В силу того что при Wi = TY = 0 жидкость не движется, т.е. а^ = 0, то соответствовать действительности будет только кривая a ( Wi ), монотонно уменьшающаяся от нуля (верхняя кривая). Поскольку именно на этой кривой для а <  1 появляется S-образная неоднозначность, которая будет приводить к физически не реализуемым решениям, то для а <  1 модифицированная модель Виноградова – Покровского может применяться только при в <  ^в yy .

Для а > 1 при в > в2 = 1, т.е. когда ayy решение проходит через область III , зависимость a (Wi) имеет разрывы, поэтому для а> 1 модифицированная модель Виноградова–Покровского может быть применена толь-

ко для в < 1. При Wi — да для а = — > 1 в

а yy

—

в

2— + в

2 а + 1

а для а <  1 а... —— —   .

yy       ₃

3.2. Исследование зависимости a ( Wi )

а = 1 . 5: 1

Рис. 2 . Зависимость a_yy ( Wi )

Рассмотрим далее зависимость a ( a ) и, соответственно, a ( Wi ). Согласно соотношению (11) a является квадратичной функцией относительно a и в зависимости от значений параметров а и в может иметь одно, два или не иметь действительных решений. Исследование дискриминанта показало, что при в <  1 а^ имеет два решения при любых значениях а и a , однако одно из них физически реализовываться не будет, т.к. од-1 но из значений а_уу будет превышать — — для

а < 1 и —      для а > 1.

2 а + 1

Для в > 1, согласно исследованию зависимости a (Wi), модифицированная модель Виноградова – Покровского дает физически реализуемые результаты при а < 1 и в < в1 , где в1 определяется по формуле (16). Зависимость a(a) и, соответственно, a (Wi)  будет однозначной только для в < вах, где

-9. .

ва„ =0 2,   7 .(

2 а - 4 а - 7

На рис. 3 приведены зависимости в1 (а) и ва (а). Например, для а = 0.5 ayy

вах » 1.06, вау, « 1.72.

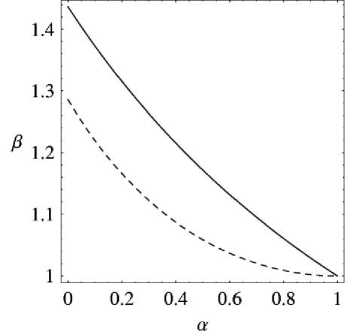
Рис. 3. Зависимости ва ( а ) и в ( а )

В области ниже сплошной кривой зависимость a ( Wi ) однозначна и монотонно убывает, в области ниже пунктирной кривой зависимость a ( Wi ) однозначна и монотонно возрастает. В области между этими кривыми зависимость a ( Wi ) имеет пик при некотором значении числа Wi , затем уменьшается и выходит на постоянную прямую (рис. 4).

Для построения зависимости a от ( Wi ) переменную Wi выразили из уравнения (14):

Wi =

а,, в2 [1 + (2к + в)а„ ](1 + а,, (2к + 4в - 3))2 (а,, + з)[ в + (2к + в) а„ ]3

. (18)

В результате a_xx ( Wi ) определяется параметрически через a_yy по формулам (11) и (18).

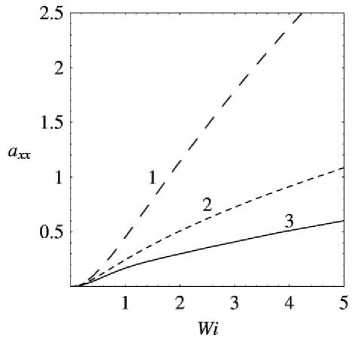
а = 1 . 5 : в = 1)0 . 1 ; 2)0 . 5 ; 3)0 . 99 .

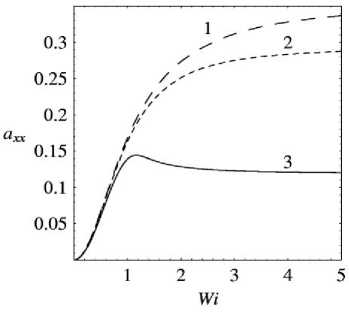
а = 0 . 5 : в = 1)0 . 99 ; 2)1 . 02 ; 3)1 . 12 .

Рис. 4 . Зависимости a от Wi xx

• 3.3.    Исследование зависимости a ( Wi )

Рассмотрим зависимость a от a и, соответственно, axy (Wi) в рамках параметров модели а ив, для которых зависимость a (Wi) однозначна. Зависимость a(a) yy                                                       xy yy является полиномом третьей степени относительно a

а,, в (1 + 2а) + а2, [1 + в (1 + 2а) | +

,                  А            ⁷      (19)

• ^а,, к + ^аХ ^в ( 1 ^{+ 2 а} ) J + ^а 2 , ^в = 0 .

Соотношение (19) может иметь одно или три действительных решения a в зави- симости от значений параметров а , в и аху . Характерный вид кривой Q = 0 для различных параметров в приведен на рис. 5.

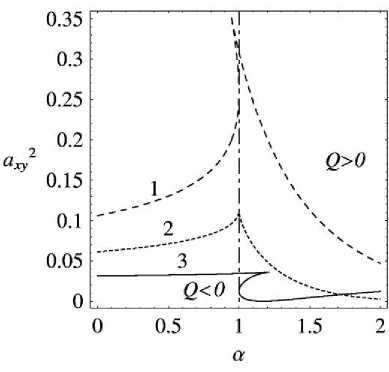
Рис. 5. Q = 0 для в = 1)0 . 3; 2)0 . 5; 3)0 . 9

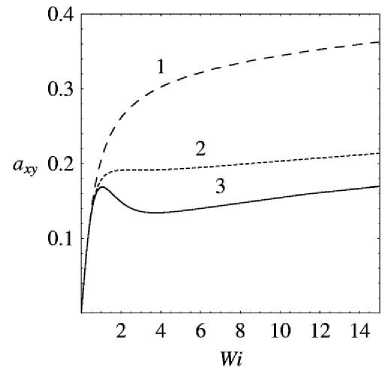
а = 1.2: в = 1) 0.5; 2) 0.89; 3) 0.99

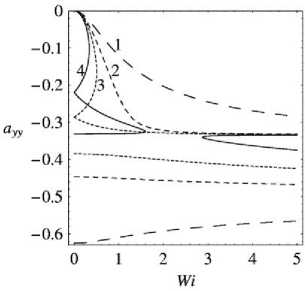
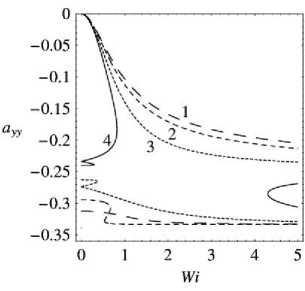
Для параметров модели, принадлежащих области ниже кривой Q = 0 , зависимость a ( a ) имеет три действительных решения ( Q <  0 ), однако исследование дискриминанта показывает, что при а <  1 физически реализовываться могут только два решения, так как одно из решений a не принадлежит области однозначности зависимости a ( Wi ).

Характерный вид зависимости a ( Wi ) для а <  1 приведен на рис. 6.

При а >  1 в области Q <  0 будут реализовываться все три решения a для некоторых значений a , в результате чего зависимость a ( Wi ) будет иметь область бифуркации (рис. 6).

Поскольку дискриминант Q сам в свою очередь является полиномом третьей степени относительно a2 , то диапазон значений пара-xy метра в, при которых возникает неоднозначность зависимости a (Wi), также можно вычислить аналитически из решения уравнения

27 + 54(а - 4) в +18(5 + 11а + 2а2) ва^ + +2(а -13)(1 + 2а)2 в^ = 0.

Например, для а = 1 . 05 неоднозначность существует в диапазоне 0 . 76 <  в <  1, для а = 1 . 2 - при 0 . 89 <  в <  1, для а = 1 . 5 -при 0 . 97 <  в < 1.

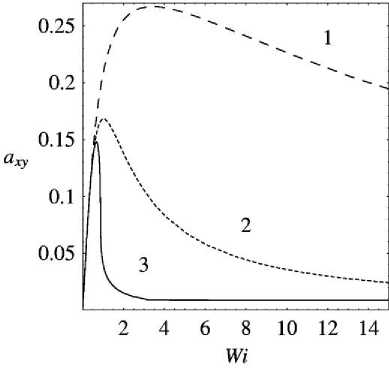
а = 0.5: в = 1)0.5; 2)0.99; 3)1.17

Рис. 6. Характерный вид зависимости a ( Wi )

• 3.4.    Исследование зависимости п* (Wi )

Безразмерная функция эффективной вязкости определяется как

. п    _ *     3

п = — = ст = — a .

п     xy Wi xy

Из соотношения (6), используя (12), определяем выражение для п *^:

.  (ayy + 3)(в + а„ (2к + в))

3в(1 + а„(2к + 4в - 3)) '

от Wi определяется системы уравнений п >  1. При Wi х

Зависимость п*  ¹

через параметр a_yy из (20) и (18). При Wi ^ 0 П * ^0.

Характерный вид данной зависимости для а >  1 и а <  1 приведен на рис. 7.

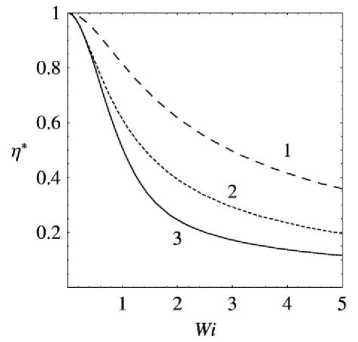
a = 1 . 5 : 1)0 . 1 ; 2)0 . 5 ; 3)0 . 99 .

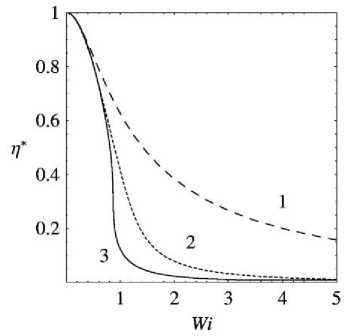
a = 0 . 5 : 1)0 . 5 ; 2)1 . 12 ; 3)1 . 17 .

Рис. 7. Зависимость П* (Wi )

Таким образом, модифицированная модель Виноградова – Покровского показывает, что в диапазоне параметров модели а и в , в котором безразмерная эффективная вязкость однозначна, сдвиговая компонента тензора экстранапряжений может иметь область бифуркации при a >  1 и пик с дальнейшим снижением и выходом на постоянное значение при а <  1 .

• 3.5.    Исследование зависимости Т * (Wi )

Безразмерные материальные функции первой и второй разности нормальных напряжений вычисляются по формуле

^ .₌^ ₌xC

^{1     T} 0 П 0

—

*

^уу     3  /         A

• —— = —г( a — a ).

i       Wi ^{2 xx yy}

Wi

Исходя из соотношений (14) и (18) выражение для Т * имеют следующий вид:

у * = 2 (ayy + 3 )(1 + ayy (2a + I))2

• ^{1   3} ( 1 + a yy (2 ав + 4 в — 3) ) 2 ^.

  
  

Зависимость Т* от Wi определяется через параметр a из системы уравнений (21) и (18). При Wi ^ 0 Т* ^ 2. При Wi ^ у (т.е. а ^^-) Т* ^ 0.

^уу 2 к + в ¹

Зависимость (21) является полиномом третьей степени относительно компоненты a и поэтому в зависимости от знака дискриминанта этого полинома может иметь один, три или не иметь действительных корней. Исследование данного дискриминанта показало, что для a > 1 и в < 1, т.е. в диапазоне однозначности зависимости a (Wi), всегда будет реализовываться одно из решений ayy , так как два других будут превышать предельное значение , к которому 2a +1

стремится а_уу при Wi ^м . Характерный вид зависимости Т * ( Wi ) для a >  1 приведен на рис. 8.

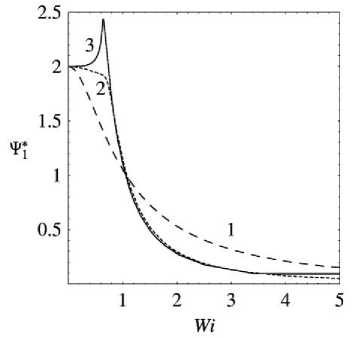
a = 0 . 1 : 1)0 . 5 ; 2)1 . 32 ; 3)1 . 36 .

Рис. 8 . Зависимость Т* (Wi )

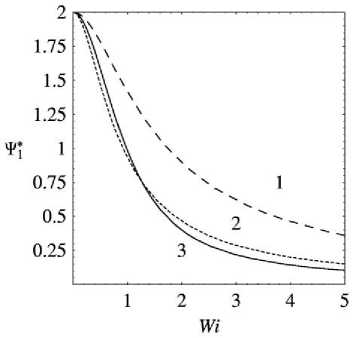
a = 1 . 5 : 1)0 . 1 ; 2)0 . 5 ; 3)0 . 99 .

При а <  1 зависимость однозначна и монотонно убывающая только для в <  в • ,

4Т которая определяется следующим образом:

_    51 а + 30

^ = 16а2 + 43а + 22 '

Например:

при а = 0.1 в,. = 1.326, а Д1  = 1.373,

• ⁴ 1                             ^ауУ

при а = 0.5 в ,. = 1.168, а Д1  = 1.172,

• ⁴ 1                             ^ayy

при а = 0.8 в,. = 1.062, а в1  = 1.06.

• ⁴ 1                         a ^аУУ

Вид зависимости в ,• ( а ) в сравнении с ⁴ 1

другими ограничениями на параметр в при а <  1 приведен на рис. 9.

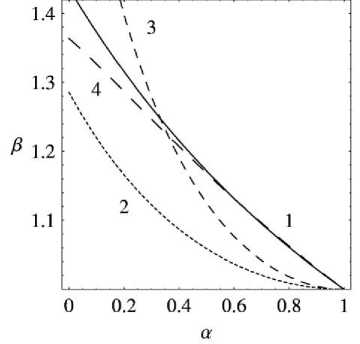
1) в yy ( а ) ; 2) ^ ( а ) ; 3) в  _ _{а >}у ( а ) ; 4) Д 4 , ( а )

Рис. 9. Вид зависимости в ,. ( а )

При в >  в . или, если в . > ^ , то при В > в зависимость 4 . (Wi ) может ^ayy                                     ¹

иметь как два, так и три подходящих действительных решения a . На рис. 4 приведен вид данной зависимости для а = 0 . 1, при котором существует пик зависимости 4 . (Wi ) (т.е. реализуются два решения), после которого значение 4 . монотонно уменьшается и выходит на постоянное значение. Для а = 0 . 5 будет существовать бифуркация при в >  в ,.

⁴ 1

(т.е. реализуются три действительных решения a_yy ), после которой данная зависимость также монотонно уменьшается, выходя на постоянное значение при Wi ^м .

Заключение

Анализ решений для сдвигового течения нелинейной упруговязкой жидкости показал:

• 1.    Модифицированная модель Покровского – Виноградова предсказывает монотонное изменение зависимости a ( Wi )  при

• 2.    Изменение зависимости a ( Wi ) при а >  1 и 0 <  Д <  1 также однозначна и монотонна. При а <  1 зависимость а_у(Wi) ) монотонна и однозначна при Д <  в , а зависи- ^ayy

• 3.    Зависимость a ( Wi ) может быть не

• 4.    Первая разность а_хх - a yy (Wi ) в диапазоне параметров модели а и Д , при которых зависимость a ( Wi ) однозначна, также

• 5.    В области параметров модели а и Д , при которых зависимость а_уу (Wi ) однозначна, эффективная вязкость ц* (Wi ) и сдвиговое напряжение однозначно и монотонно возрастают с ростом Wi . Вне этого диапазона кривая течения имеет максимум.

а > 1 и в < 1, а при а < 1 - для Д < Д1 . Вне ayy этих диапазонов параметров зависимость ayy(Wi) имеет бифуркацию.

мость a (Wi) монотонна и однозначна в бо- лее узком диапазоне Д < Д . В области

Д < Д < Д1  зависимость а^ (Wi) имеет axx              ayy                             xx пик при некотором значении числа Wi, затем уменьшается и при Wi ^м выходит на постоянное значение.

однозначной. Так, для а > 1 при Д > В axy данная зависимость будет иметь бифуркацию. Для а < 1 и Д < В1  зависимость ах„ (Wi)

axy                            xy всегда будет иметь пик, после которого зна- чение a постепенно снижается, выходя на xy постоянное значение при Wi ^ м.

однозначна и монотонно возрастает, за исключением области параметров а < 1 и Д > Д    , в котором данная зависимость ахх ауу имеет пик, после которого значение axx - ayy монотонно уменьшается, достигая постоянного значения при Wi ^м.