Sequential application of the hierarchy analysis method and associative training of a neural network in examination problems

In order to examine technical objects, it is customary to use for each object (device) a generalized quality indicator in the form of the following linear functional:

m

Jk = Y,V xkj, k = 1, 2 — K                    Ш j=1

where k is a number of one of the K compared objects, x kj are variables (features) having different nature (quantitative, qualitative, cost, etc.), which are evaluated by the experts; m is a number of features considered when examination. In general, this model is natural and does not cause difficulties. Exclusions are the cases when expert conditions are such that features area is expanded by addition of a feature of the general engineering evaluation x eng. The last feature can take negative values x_eng E [ — 1 , 1] and therefore for the successful solution of the examination problem it is necessary to apply the hierarchy analysis method (MAI) proposed by T. Saati [1].

In order to solve a direct examination problem, the values of generalized indicators Jk for all objects are determined, and then the object for which Jk takes the maximum value is selected. In the neural networks application, the built-in function compel of nntool package of the MATLAB language corresponds to the method. The function implements the following principle: "winner gets everything". However, at that the information about other examination objects is lost.

At the same time, the theory of self-organizing neural networks suggests another methodological approach to the examination problem. The approach saves information about all objects, that allows to consider their indicators in total. Therefore, there is the principle of soft maximum (softmax), based on the model of expert evaluations mixing [2]. This approach allows to get more reliable examination results, especially in cases where the objects features are very different.

The purpose of the article is to develop the examination method, based on a sequential application of the MAI method and associative training of neural networks. The proposed method is an alternative to the usual methods to solve the direct examination problem |3],

As initial data, we use the results of the evaluation of generalized quality indicators J of industrial receiving-control devices of the security-fire signal system [4] (Table). In the examination practice, in order to compare several objects it is customary to normalize the generalized indicators so that the value J _max = 1 corresponds to the best of them, and the lower values indicated in the table correspond to the rest.

Table

Normalized values of the generalized quality indicator

Devices	Tandem-IP	Inflow-GSM	Hunter- PRO	Jupiter-IP/ GPRS-8	Tandem-IP-M	Project-T
J	0,757	0,621	1,000	0,826	0,689	0,778

In addition, the features of the general engineering evaluation x_eng = — 1 and x_eng = 0 , 5 are selected for the second object "Inflow-GSM" and for the fourth object "Jupiter-IP / GPRS-8", respectively [4]. Therefore, finally vector of generalized quality indicators for compared objects takes the form

J = (0 , 757 — 0 , 379 1 , 000 1 , 326 0 , 689 0 , 778) T . (2)

The method of solving the direct examination problem was described in detail in [3]. The purpose of the method is to identify the best object in the set of compared objects by the criterion of the maximum of the generalized indicator J. In the self-organizing neural networks application, the function compel of network activation corresponds to the problem. The function belongs to the MATLAB language and implements the following principle: "winner gets everything" [5].

We apply a neural network with the activation function compel to a set of indicators (2) and graphically represent obtained results (Fig. 1).

The values of the indicator J , corresponding to the expression (2), are given in the upper part of Fig. 1, and the output signal of neural network with activation function compel is given in the bottom part of Fig. 1. As would be expected, only one (namely, the fourth) neuron "won" in the process of competition. The network outputs corresponding to other neurons are zero.

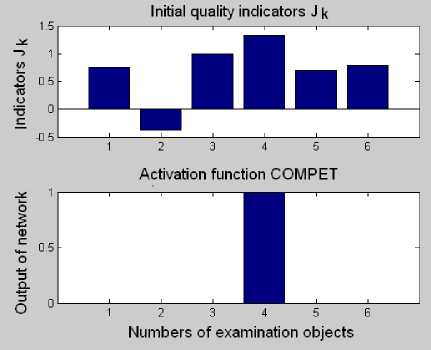
Fig. 1. The unique output of the neural network with the activation function compet

This completely corresponds to the usual method of solving a direct examination problem, since its purpose was to identify the unique object with the best indicators. However, it is follows from the bottom part of Fig. 1 that the information on indicators of other examination objects was lost.

In order to comment this situation, we refer to the opinion of the well-known specialist in neural networks, S. Khaikin [2, p. 485]: "Hard decisions, unfortunately, lead to loss of information, while soft decisions keep the information ... this empirical rule states that the information contained in the input signal can be effectively saved from a computational point of view until the system is ready finally to make decision or evaluate the parameter". Hierarchy Analysis Method. According to the method of T. Saati [1], let the examination objects ranks be in the following form

R = (3 9 2 1 3 3) T .                              (3)

We form the matrix of pairwise comparisons W, verify coordination of the matrix and determine the priority vector

S = ( 0 , 260 0 , 061 0 , 469 0 , 758 0 , 260 0 , 260 ) T .                (4)

and graphically present the results (Fig. 2, upper part).

Let us note the features of MAI applying results, comparing the results of the calculations in Fig. 1 and Fig. 2 (upper part).

• 1.    Negative value of the generalized indicator of the second object (see Fig. 1) was replaced by a positive value, although the last one is small in absolute value. This corresponds to the usual practice of applying the expert systems theory [3], when all J k E [0 , 1]. This implies that the second object is not just discarded, but has some opportunity to participate in the examination.

• 2.    The similar values of 1, 5, 6 objects indicators were replaced by the same values, 0,260. This is completely justified, since such objects can be considered as equivalent during formation of an expert opinion.

• 3.    The MAI method allows clearly separate objects on prospective and unacceptable.

Therefore, we can confirm the assumption that the MAI method is an effective tool for comparing generalized quality indicators taking into account the features of engineering evaluation.

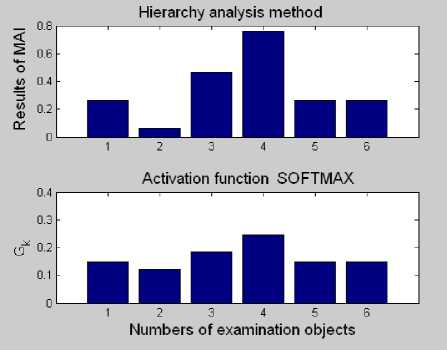
Fig. 2. Sequential application of the hierarchy analysis method and associative training of a neural network with the activation function softmax

The Method of Double-Smoothing of the Generalized Quality Indicator Values of the Examination Objects. We propose a further improvement of the quality of examination results interpretation - sequential application of the hierarchy analysis method and associative training of a self-organizing neural network.

In the analysis of Fig. 1, we noted that to form a neural network, it was advisable to replace the hard competing activation function compel by the competing activation function softmax with a soft maximum.

The activation function softmax is implemented by self-organizing neural network of "expert" opinions mixing and consists of neural networks (modules) trained with the teacher and called as experts networks, or simply experts [2]. The integrating element is called as "gateway network". It is assumed that different experts work best in their own fields of input space according to the probabilistic generating model of input data set.

Now, let indicators S, which are already formed by the MAI method (4), be sequentially fed on the input of neural network. Note that a kind of alignment of various indicators is performed and even a positive value is assigned to negative indicators during the procedure softmax. Therefore, we call outputs of neural network yk as tolerant generalized quality indicators and denote by Gk (Fig. 2, lower part).

Indeed, in this figure: 1) all indicators Gk , in the difference from the initial quality indicators Jk, have positive values; 2) the obtained indicators Gk are normalized and a sum of them is equal to unity; 3) information about all objects is saved, therefore the whole picture of examination can be evaluate better; 4) it is shown that even the second object having the negative value of indicator J ₂, has some "right" to participate in the examination.

Compare the upper and lower parts of Fig. 2. Qualitative ratio between the objects of examination is saved: still the best object is the fourth device, and the worst object is the second one. That is, the conclusions of examination remain unchanged.

The method of double smoothing of the generalized quality indicator values is an alternative to the usual "hard" approach to the solution of the direct examination problem, considered in the papers [3, 4]. It seems that the method will be particularly effective in the case of large variations in the features of the compared objects, in particular, for such objects that their features can take negative values.

The proposed methods give different possibilities for interpretation of the examination results while a whole picture of the ratio of examination objects indicators remains qualitatively unchanged.