Сеточно-характеристическая разностная схема для решения уравнения Хопфа на основе двух различных дивергентных форм
Бесплатный доступ
Построено новое двухпараметрическое семейство разностных схем для численного решения уравнения Хопфа. Исходная задача заменялась задачей для системы двух дифференциальных уравнений на основе различных дивергентных форм уравнения Хопфа. Потоковые члены выражались в виде линейных комбинаций переменных, входящих в разные дивергентные формы. В отличие от большинства работ, использующих методы неопределенных коэффициентов для построения разностных схем, при таком подходе неопределенные коэффициенты возникают при формулировке дифференциальной задачи. Система уравнений сохраняет гиперболический тип при любых значениях параметров. Для численной реализации за основу выбрана известная сеточно-характеристическая схема в инвариантах Римана, которая в случае линейного уравнения с постоянными коэффициентами переходит в схему Лакса - Вендроффа. Проведены расчеты двух тестовых задач - об эволюции гладкого начального условия и формировании разрывного решения и о распространении "ударной волны". По результатам тестовых расчетов подобраны коэффициенты экстраполяции, позволяющие получить хорошее согласие с точным решением. Исследовался апостериорный порядок сходимости к предельной функции для разрывных решений. При удачно подобранных коэффициентах экстраполяции он незначительно превышает единицу в момент градиентной катастрофы. При распространении сильного разрыва на больших временах порядок сходимости падает до 0,76. Остается открытым вопрос о постановке оптимизационной задачи, позволяющей выбирать коэффициенты экстраполяции наилучшим образом, возможно, в зависимости от локальных свойств решения. Также открытым пока остается вопрос о создании гибридных разностных схем с переменными коэффициентами экстраполяции в зависимости от гладкости решения.
Уравнение хопфа, дивергентная форма, неопределенные коэффициенты, схема лакса-вендроффа, разрывное решение
Короткий адрес: https://sciup.org/147241741
IDR: 147241741 | УДК: 519.6 | DOI: 10.14529/mmp230209
Текст научной статьи Сеточно-характеристическая разностная схема для решения уравнения Хопфа на основе двух различных дивергентных форм
Уравнения и системы уравнений гиперболического типа встречаются в большом количестве приложений. Характерной чертой решений задач для систем уравнений гиперболического типа является наличие слабых (обобщенных) решений, допускающих как разрывы самих функций, так и разрывы производных. Ввиду большого количества постановок задач для уравнений гиперболического типа не сформировался единый подход к их решению численными методами. Подробный обзор конечноразностных методов решения задач для уравнений гиперболического типа приведен в [1].
Для линейного уравнения переноса С.К. Годуновым установлена теорема, запрещающая существование монотонных конечно-разностных схем с порядком аппроксимации выше первого [2]. Хотя аналогов теоремы Годунова для произвольных уравнений и систем гиперболического типа не установлено, практически те же эффекты проявляются и при реализации численных методов для других систем уравнений гиперболического типа. Под монотонностью здесь понимается отсутствие нефизичных осцилляций численного решения. Немонотонность для схем высокого порядка аппроксимации проявляется, например, при решении уравнения Хопфа методом прямых [3].
Несмотря на большое число численных методов решения систем уравнений гиперболического типа, проблема создания разностных схем, минимизирующих как диссипативную, так и дисперсионную составляющие погрешности, по-прежнему актуальна. Известны следующие подходы к ее решению.
Использование дифференциальных следствий самого уравнения. По-видимому, исторически первый способ повышения порядка аппроксимации. В 1962 году на его основе Р.П. Федоренко построен класс гибридных схем, использующих дифференциальные продолжения в области гладкости решения (то есть там, где производные определены) [4]. Дифференциальные продолжения использованы К.М. Магомедовым и А.С. Холодовым при построении класса сеточно-характеристических численных методов [5]. Использование дифференциальных продолжений также привело к созданию класса схем повышенного порядка аппроксимации на минимальном шаблоне ( ≪ компактные разностные схемы ≫ ) [6].
Другой способ повышения порядка аппроксимации конечно-разностных схем предложен Б.В. Роговым. Он заключается в одновременном использовании в качестве расчетных переменных не только самой функции, но и интегральных средних ее значений по отрезку. Схемы, построенные подобным образом, получили название ≪ бикомпактные схемы ≫ [7, 8].
В оригинальных работах по бикомпактным схемам такие интегральные средние относились к тем же узлам сетки, что и основные переменные. В принципе можно определить переменные бикомпактной схемы на разнесенных сетках.
Третий подход к повышению пространственного порядка аппроксимации конечноразностной схемы при попытке уменьшить и диссипативную, и дисперсионную составляющую погрешности предложен сравнительно недавно. В работе В.М. Го-ловизнина и Б.Н. Четверушкина [9] построена новая консервативная балансовохарактеристическая схема. При этом для интерполяции ≪ консервативных ≫ переменных используются потоковые величины, определяемые на разнесенной сетке.
Отметим, что в настоящее время все упомянутые подходы к повышению порядка аппроксимации разностных схем активно развиваются. Число публикаций за последние годы по данной тематике велико. Кроме того, создание класса бикомпактных схем по своим идеям близко к идеям разрывного метода Галеркина [10] (где интегральное среднее по отрезку есть один из способов приближения потоковых величин). Идея введения разнесенных сеток для консервативных и потоковых переменных для повышения точности разностных схем активно применяется для построения схем в задачах с несколькими пространственными переменными. Такой подход в принципе можно считать общим как для классов бикомпактных и балансово-характеристических схем, так и для вариантов разрывного метода Галеркина.
Все упомянутые подходы объединяет общая идея – для построения разностной схемы использовать не только само уравнение, но и некоторые его следствия.
В данной работе авторами предлагается новый подход для ≪ расширения ≫ дифференциальной задачи. Как известно, для некоторых уравнений гиперболического типа существует не единственная дивергентная форма представления уравнения. Например, для квазилинейного уравнения Хопфа существует счетное число таких форм [11]. Предлагается для построения разностных схем использовать несколько дивергентных форм, объединяя их в систему уравнений, и строить разностную схему уже для системы уравнений гиперболического типа.
1. Постановка задачи
Рассмотрим следующую дифференциальную задачу для уравнения Хопфа:
∂u∂u
+ uTT" = 0'
∂t∂x
Наряду с характеристической формой записи уравнения Хопфа (1) будем рассматривать дивергентную форму записи du +1A (u2) = 0.
dt 2 dx
Эта дивергентная форма соответствует закону сохранения импульса.
Выберем теперь другую дивергентную форму записи уравнения (1). Так как решение (1) отлично от тождественного нуля, то его можно переписать в виде
1 du du
— я7 + я- = 0'
u ∂t ∂x
Введем новую переменную v = In | u | , тогда последнее равенство будет иметь вид
∂v ∂u
+ я- = 0'
∂t ∂x
Это – следствие исходного уравнения (1). Обратное преобразование, переводящее решение (3) в решение (1) — u = sign (u)e v .
Для уравнения (1) потоковое слагаемое представим в виде линейной комбинации потоков, вычисленных с использованием функций u и v :
ди + 2 £ ( ви 2 + (1 - в ) e 2v ) =0,
где в > 0 .
Если теперь рассматривать систему уравнений (3), (4) и решать ее численно, то сеточная функция u будет представлять собой сеточную проекцию решения уравнения Хопфа. Такая форма системы уравнений будет самой простой, но, к сожалению, численные результаты в этом случае получаются неудовлетворительными.
Для получения нового семейства разностных схем введем параметр а > 0 и представим потоковое слагаемое в (3) по аналогии с (4). Получим систему нелинейных уравнений в частных производных
^t + 2дХ ( в" 2 + (1 — в ) e 2 v ) =°.
Iv + It (аи + (1 — а) sign (u) e v ) = 0. ∂t ∂x
Начальные и граничные условия для системы будут сформулированы ниже при описании результатов расчетов тестовых задач.
В систему нелинейных дифференциальных уравнений входят два неопределенных коэффициента. В отличие от большинства работ, использующих методы неопределенных коэффициентов для построения разностных схем, при таком подходе неопределенные коэффициенты возникают при формулировке дифференциальной задачи.
Отметим, что использование методов неопределенных коэффициентов широко использовалось при построении сеточно-характеристических схем [5]. Пространства неопределенных коэффициентов для построения линейных разностных схем впервые были введены в [11]. В [12] на основе анализа в пространствах неопределенных коэффициентов построены гибридные неосциллирующие схемы высокого порядка аппроксимации для нелинейных систем уравнений гиперболического типа.
Известно [13], что (1) допускает запись в виде бесконечного числа дивергентных форм. Форма (1) и дивергентная форма, учитывающая закон сохранения энергии для уравнения Хопфа, использовалась для анализа семейства разностных схем в пространстве неопределенных коэффициентов для решения уравнения Бюргерса с преобладающей конвекцией [14].
В ходе эволюции даже гладкого начального возмущения при решении уравнения Хопфа могут сформироваться разрывы [15]. Классическое решение уравнения перестает существовать, существует только слабое (обобщенное) решение. Актуальным является проблема построения разностных схем, позволяющих правильно воспроизводить явление градиентной катастрофы, правильно воспроизводить скорость фронта и давать минимальные осцилляции при возникновении разрывов решения.
2. Сеточно-характеристическая схема второго порядкааппроксимации по пространству
В качестве рабочей схемы строится вариант сеточно-характеристической схемы [5], имеющий второй порядок аппроксимации по пространственной переменной. Несмотря на то, что схема фиксирована, она погружена в двумерное пространство неопределенных коэффициентов. В случае, когда 0 < а, в < 1 , выполняется интерполяция при вычислении пространственных производных для обеих переменных, в противном случае – экстраполяция хотя бы для одной переменной.
Для построения разностной схемы перепишем систему в характеристической форме
£ f u ^ + (в u (1 - в ) e 2v 2 Л (А = 0 (5)
dt V/ \а (1 — а) sign (u)e v/ dx \v) ' U
Собственные числа матрицы системы (5) будут
А х = 2 [в u + (1 - а) sign (u)e v ] + V D ,
А2 = 2 [[вu + (1 — а) sign(u)ev] - VD^ , здесь D — дискриминант возникающего квадратного уравнения
D = [в u + (1 — а) sign (u)e v ] 2 — 4 [ в (1 — а) | u | e v — а (1 — в) e 2 v ] •
Для точного решения уравнения Хопфа должно выполняться равенство e 2v = u 2 , тогда, после упрощения, получим следующую оценку дискриминанта:
D = (в — 1 — a) 2 u 2 . (6)
Из (6) следует, что собственные числа всегда действительные, тогда система (5) имеет гиперболический тип при любых значениях параметров α и β .
Соответствующие левые собственные векторы для собственных чисел матрицы системы (5) выписаны ниже:
"^ i — (a, A i — в и ), J 2 — (a, A 2 — в и ).
При переходе в базис из левых собственных векторов система уравнений расщепляется. При этом возникают новые расчетные переменные – инварианты Римана. Для системы (5) они имеют вид:
I 1 — au + (A 1 — в и ) v,
I 2 — au + (A 2 — в и ) v.
Обратный переход от инвариантов Римана к естественным переменным задачи u и v осуществляется пересчетом
(и^ — — 1 (A 2 v α √ D
- β u
- α
β u - α
λ 1 II 12 .
Введем некоторые ограничения на выбор параметров α и β . Для собственных чисел матрицы (5) с учетом (6) получаем оценки
A i — 2 [( в +(1 — a )) u + |в — 1 — a| l u l ],
A 2 — ^[( в +(1 — a )) u — |в — 1 — a| | u | ] •
Потребуем сначала, чтобы при положительном значении u оба собственных числа были неотрицательными. Как легко показать, для этого требуется выполнение условия β ≥ α. Потребуем далее, чтобы при отрицательном значении u первое собственное число было неотрицательным, а второе – неположительным. Для выполнения этого требования должно выполняться неравенство β ≤ α.
Построим теперь двухпараметрическое семейство сеточно-характеристических схем. В расчетной области введем равномерную расчетную сетку по времени t и по пространству x :
t n — n т, x k — x 0 + kh, k — 0, N.
Значения u и v при n — 0 задаются начальными условиями. Значения и и v при k — 0 (или при k — N , в зависимости от постановки задачи) задаются граничными условиями. Для расчетов будем использовать разностную схему второго порядка аппроксимации по пространственным переменным. В качестве основы для построения схемы выбран вариант сеточно-характеристической схемы [5]. В случае линейного уравнения переноса с постоянными коэффициентами она переходит в известную схему Лакса – Вендроффа. Разностные уравнения для инвариантов Римана выглядят следующим образом.
Если u m > 0 , тогда
(i i ) m +1 — (1 — (^ i ) m )(i i ) m +(^ i ) m (i i ) m - i
(I 2 ) m +1 — (1 — (^ 2 ) m )(i 2 ) m +(^ ) m (1 2 ) m - i
— 2 (( a i ) m ) 2 ( ( i i ) m +i — 2 (I i ) m +(I i ) m - i ) , — 2 (( a 2 ) m ) 2 ( (I 2 ) m +i — 2 ( I 2 ) m +(I 2 ) m - i ) ,
здесь введены обозначения (^ i ) m и (^ 2 ) mm для локальных значений чисел Куранта для
|
инвариантов |
г х n = т (А 1 ) т n т (A 2 ) m ( a i ) m h , ( а 2 ) m h • |
Если u m < 0 , тогда
к) m +1 = (1 - (^ 1 ) m ) (i i ) m + <» i ) m (a ) m — i - 2 (№ 2 ( (i i ) m +i - 2 № + (i i ) m — i ) ,
№) m +1 = (1 + (^ 2 C.) (AX m — (^ 2 ) m (I 2 ) m +1 — 2 (№ 2 ( ( AXm +i — 2 (I 2 ) m + (I 2 ) m - 1 ) .
Значения и и v естественных переменных на (n + 1)-м временном слое восстанавливаются uv
n +1
т
1 ЛЛ 2 - в и) ’
[(аД 2 ) ’ - (аА 1 ) ’ ] V -а ’
-
(A i - в u )mA ЛЛ
α n m I 2
n +1
m
Для устойчивости разностной схемы потребуем выполнения условия Куранта
h
т< max( | A i | , ^Dm'
m
3. Результаты тестовых расчетов
С помощью численной реализации описанной разностной схемы проведены численные расчеты нескольких тестовых задач. Результаты показывают, что лучшие результаты разностная схема дает при использовании экстраполяции в дифференциальной задаче а > 1,в > 1. При а = 1,в = 1 уравнения в системе расщепляются, для решения первого уравнения системы предложенная разностная схема переходит в традиционный вариант схемы Лакса – Вендроффа.
Тестовая задача 1. В качестве начальных условий выбираем гладкую функцию и (0, x) = A- ch-2 x.
Известно, что в ходе эволюции данного начального возмущения теряется гладкость [15], в решении образуется сильный разрыв.
Начальные условия для функции v очевидны, v (0,x) = ln A - 2ln(ch 2). Для определенности положим A = 1 . В качестве граничных условий выбираем условия периодичности на отрезке x G [ - 5, 5]
и (t, - 5) = и (t, 5) .
На рис. 1 приведены график точного решения задачи, построенного методом характеристик (пунктирная линия), и графики численного решения на сетке с 3200 ячейками по пространственной переменной и значении числа Куранта 0,4 при значениях параметров а = 1, 01 и в = 1,1 (сплошная линия) и а = 1,1 и в = 1,15 (штриховая линия) для времени T = 2, 598 (момент градиентной катастрофы). Пройдено 2079 шагов по времени. Видно, что совпадение графиков удовлетворительное, но численное решение несколько опережает точное из-за того, что численная погрешность носит преимущественно дисперсионный характер.
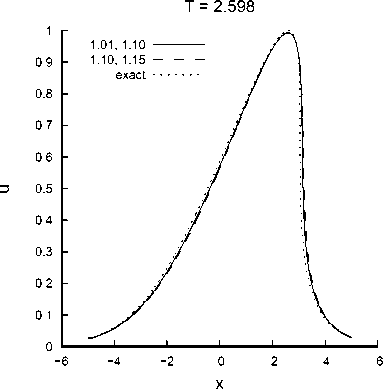
Рис. 1 . Сравнение численного решения при значениях параметров 1,01 и 1,1 (сплошная линия) и 1,1 и 1,15 (штриховая линия) с точным решением дифференциальной задачи, построенным методом характеристик, (пунктирная линия) для времени T = 2,598 (момент градиентной катастрофы)
Для количественной оценки порядка сходимости к предельной сеточной функции при утрате гладкости решения вычислялась норма разности численных решений на различных сетках (аналог нормы L2) при фиксированном времени
M
err 2 =
h^ (u n - U 32Oo (X i ,t n )) 2 .
i =0
Расчет проводился на последовательности сгущающихся сеток с числом ячеек 100, 200, 400, 800, 1600 при максимальном значении числа Куранта 0,4. Здесь число Куранта вычислялось по начальным данным, k = h • max ( | А 1 | , | А 2 | ) 0 . Зависимость нормы погрешности от шага по пространственной координате приведена на рис. 2 в двойных логарифмических координатах. Апостериорный порядок сходимости определялся тангенсом угла наклона прямой, построенной по расчетным данным методом наименьших квадратов. Для момента градиентной катастрофы он оказался равным 1,02 для а = 1, 01 и в = 1,1 (сплошная линия) и 1,05 для а = 1,1 и в = 1,15 (штриховая линия).
На рис. 3 показана зависимость нормы погрешности в зависимости от шага по времени при фиксированном шаге по пространственной переменной (от числа Куранта). Расчеты проводились для значений числа Куранта (cv) 0,4, 0,2, 0,1, 0,05, график приведен в двойных логарифмических координатах. Для рассматриваемой разностной схемы погрешность, связанная с изменением шага по времени, существенно меньше погрешности, определяемой пространственной дискретизацией, поэтому схема практически нечувствительна к изменению шага по времени (числа Куранта).
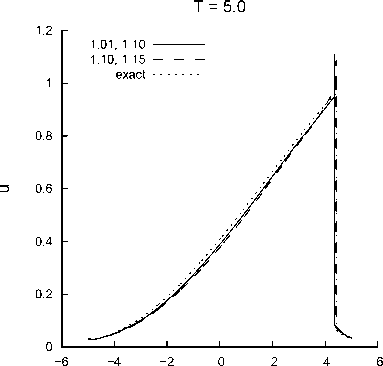
Аналогичные оценки проведены для времени 5,0 (после 4000 шагов по времени) На рис. 4 приведены график точного решения задачи, построенного методом характеристик (пунктирная линия) и графики численного решения на сетке с 3200 ячейками по пространственной переменной и значении числа Куранта 0,4 при значениях параметров а = 1, 01 и в = 1,1 (сплошная линия) и а = 1,1 и в = 1,15 (штриховая линия). Видно, что совпадение графиков удовлетворительное, но теперь наметилось
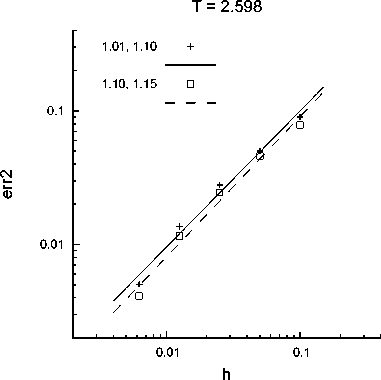
Рис. 2 . Оценка порядка сходимости схемы для момента градиентной катастрофы
0.01
T = 2.598
1.01, 1.10
1.10, 1.15 — ч- —
0.1 cv
J
Рис. 3 . Оценка зависимости погрешности разностной схемы от шага по времени (числа Куранта) для момента градиентной катастрофы
некоторое отставание фронта численного решения от точного. Это отставание можно объяснить тем, что для численного решения нарушаются имеющиеся в задаче законы сохранения (построенная схема неконсервативна). Так как в основу построения разностной схемы положена немонотонная схема Лакса – Вендроффа для каждого инварианта, то можно ожидать, что построенная схема немонотонна. Рис. 4 иллюстрирует появление нефизичных осцилляций в окрестности разрыва.
x
Рис. 4 . Сравнение численного решения при значениях параметров 1,01 и 1,1 (сплошная линия) и 1,1 и 1,15 (штриховая линия) для времени T = 5,0 (пройдено 4000 шагов по времени) с точным, построенным методом характеристик (пунктирная линия)
Для количественной оценки порядка сходимости при времени 5,0 также использована норма (7). Расчет проводился на последовательности сгущающихся сеток с числом ячеек 100, 200, 400, 800, 1600 при фиксированном числе Куранта 0,4. Зависимость нормы погрешности от шага по пространственной координате приведена на
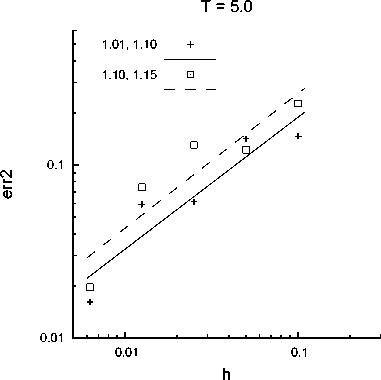
Рис. 5 . Оценка порядка сходимости схемы для момента T = 5,0
T = 5.0
1.01, 1.10
1.10, 1.15
0.01 0.01 0.1 1
cv
Рис. 6 . Оценка погрешности схемы для момента T = 5,0 при изменении шага по времени (числа Куранта)
рис. 5 в двойных логарифмических координатах. Апостериорный порядок сходимости определялся тангенсом угла наклона прямой, построенной по расчетным данным методом наименьших квадратов. Порядок сходимости разностной схемы оказался равным 0,76 для а = 1, 01 и в = 1,1 (сплошная линия) и 0,78 для а = 1,1 и в = 1,15 (штриховая линия).
На рис. 6 показана зависимость нормы погрешности в зависимости от шага по времени (от числа Куранта) при фиксированном шаге по пространственной переменной для времени T = 5, 0 . Расчеты проводились для чисел Куранта (cv) 0,4, 0,2, 0,1, 0,05. график приведен в двойных логарифмических координатах. Для рассматриваемой разностной схемы погрешность, связанная с изменением шага по времени, существенно меньше погрешности, определяемой пространственной дискретизацией, поэтому схема и для этого момента практически нечувствительна к изменению шага по времени (числа Куранта).
Тестовая задача 2 . Разные авторы проводят тестирование своих разностных схем на отличных друг от друга постановках задач. В работе [16] приведены результаты тестирования схемы (разрывный метод Галеркина) на точном разрывном решении уравнения Хопфа:
{x + 1 / х т—7 ,x ------, X > Xf (t) t+1 f Такого рода решение моделирует распространение ударных волн в газе. Используем это решение в качестве тестового. В качестве начальных данных бралось значение точного решения при t = 0, в качестве граничного значения на каждом временном слое при x = 0 бралось значение точного решения в этой точке при соответствующем моменте времени. Предложенная разностная схема использована для воспроизведения данного разрывного решения на сетке, совпадающей с использованной в [16] (400 и 800 ячеек по пространству). Расчеты велись с числом Куранта 0,4. Наилучшее совпадение с точным решением достигнуто при значениях коэффициентов а = в = 1, 0365. Рис. 7. Сравнение численного решения для t = 0,5 и сеток с числом ячеек 400 (штриховая линия) и 800 (сплошная линия) по пространственной переменной с точным решением (пунктирная линия) T = 5.0 0.1 0.09 0.08 0.07 0.06 0.05 0.04 0.03 0.02 0.01 400 cells I 800 cells I 0 0.2 0.4 0.6 0.8 Рис. 8. Погрешность приближенного решения при времени 0,5 для сеток с 400 ячейками (штриховая линия, 500 шагов по времени) и 800 ячейками (пунктирная линия, 1000 шагов по времени) Сравнение численного и точного решения для времени 0,5 приведено на рис. 7. Видно, что на данном тесте качество приближения заведомо не хуже, чем для разрывного метода Галеркина [16]. На рис. 8 приведена погрешность численного решения для времени 0,5 (500 и 1000 шагов по времени для сеток 400 и 800 ячеек по пространству соответственно). В области гладкости функции погрешность незначительна. Она возрастает в окрестности разрыва решения. Несмотря на то, что при сгущении сетки имеется стремление к точному решению, амплитуда графика погрешности в окрестности разрыва остается примерно постоянной. Заключение Для повышения априорного порядка аппроксимации разностных схем и уменьшения нефизичных осцилляций на разрывах при построении разностных схем обычно применяются некоторые дополнительные условия, представляющие собой следствия исходного дифференциального уравнения. Это могут быть, например, дифференциальные продолжения или интегральные средние на сетке. При использовании таких подходов можно применить метод анализа разностных схем в пространстве неопределенных коэффициентов для построения разностной схемы. В предлагаемом подходе введение в рассмотрение неопределенных коэффициентов предполагается на этапе формулировки дифференциальной задачи. Мы рассматриваем проблему построения разностной схемы для квазилинейного уравнения гиперболического типа (уравнения Хопфа) как проблему построения схемы для системы уравнений, причем для потоковых переменных выполняется экстраполяция на основе использования двух дивергентных форм. Тестовые расчеты показали, что при удачном выборе коэффициентов экстраполяции разностная схема показывает неплохие результаты на разрывных решениях уравнения Хопфа. При проведении численных расчетов неопределенные коэффициенты подбирались вручную. Открытым остается вопрос о постановке оптимизационной задачи, позволяющей выбирать коэффициенты экстраполяции наилучшим образом, возможно, в зависимости от локальных свойств решения. Также открытым пока остается вопрос о создании гибридных разностных схем (с переменными коэффициентами экстраполяции и разными аппроксимационными свойствами в зависимости от гладкости решения).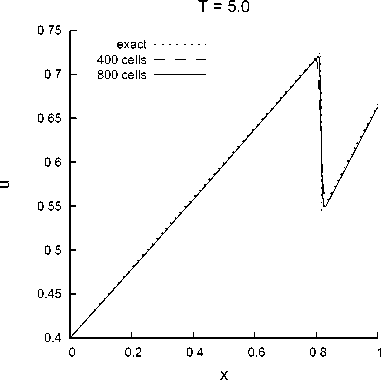
Список литературы Сеточно-характеристическая разностная схема для решения уравнения Хопфа на основе двух различных дивергентных форм
- Куликовский, А.Г. Математические вопросы численного решения гиперболических систем уравнений / А.Г. Куликовский, Н.В. Погорелов, А.Ю. Семенов. - М.: Физматлит, 2012.
- Годунов, С.К. Разностный метод численного расчета разрывных решений уравнений гидродинамики / С.К. Годунов // Математический сборник. - 1959. - Т. 47 (89), № 3. -С. 271-306.
- Гужев, Д.С. Уравнение Бюргерса - тест для численных методов / Д.С. Гужев, Н.Н. Калиткин // Математическое моделирование. - 1995. - Т. 7, № 4. - С. 99-127.
- Федоренко, Р.П. Применение разностных схем высокой точности для численного решения гиперболических уравнений /Р.П. Федоренко // Журнал вычислительной математики и математической физики. - 1962. - Т. 2, № 6. - С. 1122-1128.
- Магомедов, К.М. Сеточно-характеристические численные методы / К.М. Магомедов, А.С. Холодов. - М.: Юрайт, 2017.
- Толстых, А.И. Компактные и мультиоператорные аппроксимации высокой точности для уравнений в частных производных / А.И. Толстых. - М.: Наука, 2015.
- Рогов, Б.В. Монотонные бикомпактные схемы для линейного уравнения переноса / Б.В. Рогов, М.Н. Михайловская // Математическое моделирование. - 2011. - Т. 23, № 6. - С. 98-110.
- Аристова, Е.Н. Бикомпактные схемы для неоднородного линейного уравнения переноса / Е.Н. Аристова, Д.Ф. Байдин, Б.В. Рогов // Математическое моделирование. - 2013. -Т. 25, № 5. - С. 55-66.
- Головизнин, В.М. Алгоритмы нового поколения в вычислительной гидродинамике / В.М. Головизнин, Б.Н. Четверушкин // Журнал вычислительной математики и математической физики. - 2018. - Т. 58, № 8. - С. 20-29.
- Cockburn, B. An Introduction to the Discontinuous Galerkin Method for Convection-Dominated Problems / B. Cockburn // Lecture Notes in Mathematics. - Berlin: SpringerVerlag, 1998. - P. 151-268.
- Холодов, А.С. О построении разностных схем с положительной аппроксимацией для уравнений гиперболического типа / А.С. Холодов // Журнал вычислительной математики и математической физики. - 1978. - Т. 18, № 6. - С. 1476-1492.
- Холодов, А.С. О критериях монотонности разностных схем для уравнений гиперболического типа / А.С. Холодов, Я.А. Холодов // Журнал вычислительной математики и математической физики. - 2006. - Т. 46, № 9. - С. 1638-1667.
- Федоренко, Р.П Введение в вычислительную физику / Р.П. Федоренко. - Долгопрудный: Интеллект, 2009.
- Basharov, I.V. On the Finite Difference Schemes for Burgers Equation Solution / I.V. Basharov, A.I. Lobanov // Smart Modelling for Engineering Systems. - Singapore, 2021. - V. 215, P. 151-167.
- Уизем, Дж.Б. Линейные и нелинейные волны / Дж.Б. Уизем. - М.: Мир, 1977.
- Криксин, Ю.А. Построение точных решений некоторых уравнений гиперболического типа, содержащих разрыв, распространяющийся по неоднородному фону /Ю.А. Криксин, П.А. Кучугов, М.Е. Ладонкина, О.А. Неклюдова, В.Ф. Тишкин // Препринты Института прикладной математики им. М.В. Келдыша. - М., 2018. - № 17. - 14 c.


