Сглаживание трендов динамических рядов в задачах управления персоналом
Автор: Крученецкий В.З., Айдауова А.А., Крученецкий В.В.
Журнал: Вестник Алматинского технологического университета @vestnik-atu
Рубрика: Техника и технологии
Статья в выпуске: 4 (113), 2016 года.
Бесплатный доступ
Рассмотрены методы сглаживания линий трендов динамических рядов, используемых в задачах управления персоналом ВУЗа, в частности прогнозирования. Дан анализ методов и моделей трендов динамических рядов. Результаты сглаживания приведены на реальном при-мере тренда методами скользящей средней, последовательных разностей и экспоненциаль-ного сглаживания. Проведенные исследования позволяют повысить качество прогнозирова-ния в управлении персоналом ВУЗа.
Тренд, мультипликативная модель, аддитивная модель, прогнозиро-вание, сглаживание
Короткий адрес: https://sciup.org/140204897
IDR: 140204897 | УДК: 004:350.081
Текст научной статьи Сглаживание трендов динамических рядов в задачах управления персоналом
Как известно, в современном мире, в условиях воздействия внутренних и внешних переменных факторов, изменчивой экономики, менеджеры должны предугадывать изменения и их влияние на результаты работы c тем, чтобы адекватно на них реагировать. Одним из методов, позволяющих обеспечить точное планирование, является прогнозиро- вание, в котором предсказание будущего опирается на накопленный опыт и текущие предположения относительно будущего. Ко всему, прогнозирование является одной из важнейших функций управления персоналом [1,2].
Статистические методы в прогнозировании играют решающую роль. При этом важное место и значение занимают динамические, в том числе временные ряды. Для описания временных рядов требуется определенная модель. Модели отличаются большим разнообразием, из которых наиболее распространенными являются аналоговые, математические. Последние, представляющие собой систему уравнений и позволяющие получить некий набор искусственных данных в форме временных рядов, в данном случае являются основными.
Прогнозированию, как и любому другому процессу с использованием динамических рядов, присущ алгоритм, который включает следующие пошаговые действия:
-
1. Выбор совокупности моделей динамических рядов.
-
2. Оценка конкретной модели (в рамках совокупности), которая позволяет получить искусственные данные, отвечающие важнейшим характеристикам анализируемого ряда.
-
3. Представление прогноза ожидаемого значения будущего поведения модели, для которой сделана оценка.
Границами прогноза являются доверительные интервалы и при условии, если используемая модель корректна, будущее наблюдение с вероятностью, например, 95%, попадет в эти границы. Границы прогноза вычисляются обычным способом на основании стандартной ошибки, которая представляет изменчивость будущего поведения оцениваемой модели [1,3].
Объекты и методы исследования
В качестве объектов исследования рассматриваются тренды динамических рядов, используемых в задачах управления персоналом, в частности, прогнозирования. При анализе временного ряда используются различные методы и подходы в прогнозировании. В данной работе дано как теоретическое описание основных методов анализа трендов динамических рядов, их сглаживания, так и их практическое воплощение.
Основная тенденция изменения временного ряда выражается трендом (тренд - от англ. trend — тенденция). Тренды могут быть описаны различными уравнениями — линейными, логарифмическими, степенными и др. Фактический тип тренда устанавливают на основе подбора его функциональной модели статистическими методами, либо сглаживанием исходного временного ряда. В экономике, например, тренд - направление преимущественного движения показателей. Обычно рассматривается в рамках технико-экономи- ческого анализа, где подразумевают направленность движения цен или индексов.
Выделяют тренды восходящий (бычий), нисходящий (медвежий) и боковой (флэт). На графике часто рисуют линию тренда, которая на восходящем тренде соединяет две или более впадины, например, цены (линия находится под графиком, визуально его поддерживая и подталкивая вверх), а на нисходящем тренде соединяет два или более пика цены (линия находится над графиком, визуально его ограничивая и придавливая вниз). Трен -довые линии являются линиями поддержки (для восходящего тренда) и сопротивления (для нисходящего тренда). При восходящем тренде последующий пик на графике должен быть выше предыдущих; при нисходящем тренде - последующие спады на графике должны быть ниже предыдущих [1,3].
Методы оценки трендов также отличаются разнообразием. Различают параметрические и непараметрические методы. Первые (параметрические) — рассматривают временной ряд как гладкую функцию по времени, т.е. от t:
. (1)
При этом сначала выявляют один, либо несколько допустимых типов функций .!' :; затем различными методами (например, методом наименьших квадратов) оценивают параметры этих функций, после чего на основе проверки критериев адекватности выби -рают окончательную модель тренда. Важное значение для практических приложений имеют линеаризованные тренды, то есть тренды, приводимые к линейному виду относительно параметров с использованием тех или иных алгебраических преобразований. Вторые (непараметрические) — это разные методы сглаживания исходного временного ряда: скользящие средние (простые, взвешенные), экспоненциальное сглаживание. Эти методы применяются как для оценки тренда, так и для прогнозирования. Они особенно полезны в случае, когда для оценки тренда не удается подобрать подходящую функцию.
Основное предположение, лежащее в основе анализа временных рядов, состоит в следующем: факторы, влияющие на исследуемый объект в настоящем и прошлом, будут влиять на него и в будущем. Таким образом, основные цели анализа временных рядов заключаются в идентификации и выделении факторов, имеющих значение для прогнозирования. Чтобы достичь этой цели, разработано множество математических моде- лей, предназначенных для исследования колебаний компонентов, входящих в модель временного ряда [1]. В их числе наибольшее распространение получили аддитивная и мультипликативная модели. Отличие в формулах, представляющих эти модели, является то, что в первой модели компоненты складываются, а во второй - перемножаются. Наиболее распространенной является классическая мультипликативная модель для ежегодных, ежеквартальных и ежемесячных данных. Ее основными компонентами являются: цикли-
Таблица 1 - Данные валового дохода организации ческий, нерегулярный и сезонный компоненты, тренд.
Результаты и их обсуждение
Тренд – это долговременная тенденция (закономерность) в изменении уровней ряда. В таблице 1 приведен временной ряд валового дохода реальной организации. Изображение временного ряда по этим данным наглядно иллюстрируют рост валового дохода (рис. 1). Как видим, на протяжении 20 лет рост доходов организации имел возрастающую тенденцию.
|
Годы |
Доходы (тыс. тенге) |
Годы |
Доходы (тыс. тенге) |
|
1992 |
581.4 |
2002 |
1301.3 |
|
1993 |
581.7 |
2003 |
1440.5 |
|
1994 |
590.6 |
2004 |
1661.2 |
|
1995 |
620.4 |
2005 |
1769.8 |
|
1996 |
700.0 |
2006 |
1850.6 |
|
1997 |
781.1 |
2007 |
1954.3 |
|
1993 |
891.5 |
2008 |
2023.5 |
|
1999 |
993.0 |
2009 |
2079.3 |
|
2000 |
1110.5 |
2010 |
2145.8 |
|
2001 |
1149.0 |
2011 |
2429.6 |
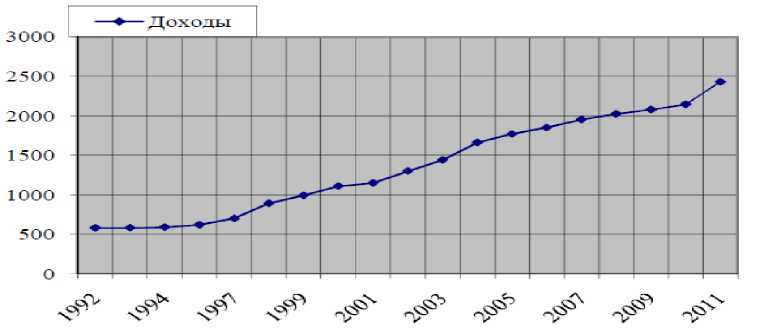
Рис. 1 Динамический ряд валового дохода.
Необходимо отметить, что тренд - не единственный компонент временного ряда; так в состав мультипликативной модели временного ряда входит: сезонный, циклический и нерегулярный компоненты [1]. Циклический компонент описывает колебание данных, часто коррелируя с циклами деловой активности. Его длина изменяется обычно в интервале от 2 до 10 лет. Частота и амплитуда циклического компонента также не постоянны. В некоторые года данные могут иметь значения выше, предсказанного трендом, а в другие годы – ниже. Любые наблюдаемые данные, не лежащие на кривой тренд и не подчиняю- щиеся правилам циклической зависимости, являются случайными компонентами, если данные записываются ежедневно или ежеквартально, возникает компонент, называемый сезонным [1,3].
Классическая мультипликативная модель динамического ряда утверждает, что любое наблюдаемое значение является произведением перечисленных компонентов и выражается следующим образом:
Y = Tt*Ct*It , (2)
где T i – значение тренда, С i – значение циклического компонента в i-м году,
I i – значение случайного компонента в i-м году.
Если данные измеряются ежемесячно или ежеквартально, наблюдение Y i , соответствующее i-му периоду, выражается уравнением:
Trl = Tl*SuCl*Il, (3)
где T i – значение тренда, S i – значение сезонного компонента в i-м периоде, С i – значение циклического компонента в i-м периоде, I i – значение случайного компонента в i-м периоде [1].
Как отмечено выше, простейшим подходом к моделированию временных рядов, содержащих сезонные колебания, является построение аддитивной или мультипликативной моделей временного ряда. Выбор одной из этих моделей основывается на анализе его структуры. Если амплитуда сезонных колебаний примерно постоянна, то строят аддитивную модель. Если же она непостоянна, то есть возрастает или уменьшается, то строят мультипликативную модель. Чаще всего при изучении спроса, роста цен и других рыночных показателей строится аддитивная модель временного ряда.
На динамику изучаемого показателя действует множество факторов, среди которых важное место занимают сезонные колебания, инфляция, кризисы, появление конкурирующей продукции и т.д. Условно показатели можно разделить на два вида – циклические и нециклические. Циклические – это все виды сезонных и повторяющихся временных колебаний. Нециклические – случайные показатели, влияющие на спрос, а также трендовые компоненты.
Существуют такие динамические ряды, в которых не совсем понятна закономерность, т.е тенденция изменения данных слабо выражена или вообще отсутствует. В этом случае наиболее распространенным приемом для устранения «аномальных» значений данных является сглаживание временного ряда. Рассмотрим пример колебаний средней численности работников университета (каждого последующего года по отношению к предыдущему). В таблице 2 приведены данные за 12 лет, на рис.3 дана диаграмма их разброса.
Таблица 2 - Изменения численности персонала университета.
|
Год |
Изменения численности, в % |
Год |
Изменения численности, в % |
|
1991 |
14,4 |
1997 |
16,5 |
|
1992 |
17,2 |
1998 |
12,9 |
|
1993 |
16,3 |
1999 |
14,4 |
|
1994 |
14,4 |
2000 |
15,6 |
|
1995 |
11,6 |
2001 |
19,4 |
|
1996 |
12,6 |
2002 |
18,3 |
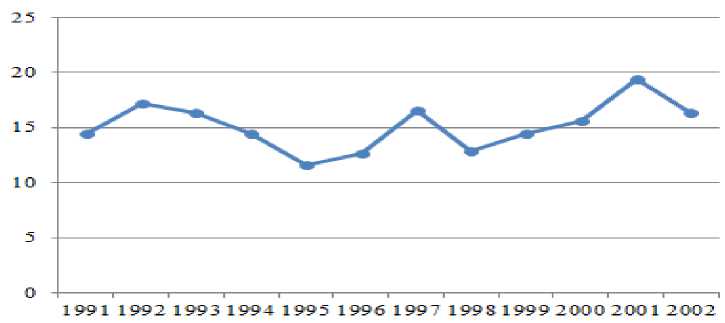
Рис. 3 Диаграмма разброса численности персонала университета.
Как видно из рис.3, временной ряд имеет большое число колебаний и, таким образом, визуальный анализ графика не позволяет утверждать, что данные имеют тренд и определенную закономерность. В таких случаях применяются методы сглаживания.
Существует три основных метода сглаживания: скользящей средней, последова- тельных разностей и метод экспоненциального сглаживания. Рассмотрим их на указан- ном выше примере изменения численности персонала университета.
Метод скользящих средних субъективен и зависит от длины периода L, выбранного для вычисления средних значений. Для того, чтобы исключить циклические колебания, длина периода должна быть целым числом, кратным средней длине цикла. Скользящие средние для выбранного периода, имеющего длину L , образуют последовательность средних значений, вычисленных для последовательностей длины L . Обозначаются обычно символами MA(L) .
Предположим, что мы хотим вычислить пятилетние скользящие средние значения по данным, измеренным в течение n =11 лет. Поскольку L =5, пятилетние скользящие средние образуют последовательность средних значений, вычисленных по пяти последовательным значениям временного ряда. Первое из пятилетних скользящих средних значений вычисляется путем суммирования данных о первых пяти годах с последующим делением на пять; тогда формула скользящей средней примет вид:
MA(5^ = К 1 +Г 2 +У З +У 4 + 1-'5
Второе пятилетнее скользящего сред- него вычисляется путем суммирования данных о годах со 2-го по 6-й с последующим делением на пять:
2 2 +У 3 +К 4 +У 5 +У 6
МЛ(5) =
Третье пятилетнее скользящего сред- него вычисляется путем суммирования данных о годах со 3-го по 7-й и для последующих пятилетий этот процесс продолжается, пока не будет вычислено скользящее среднее для последних пяти лет. Работая с годовыми данными, следует полагать число L (длину периода, выбранного для вычисления скользящих средних) нечетным. В этом случае невозможно вычислить скользящие средние для первых (L – 1)/2 и последних (L – 1)/2 лет. Следовательно, при работе с пятилетними скользящими средними невозможно выполнить вычисления для первых двух и последних двух лет. Год, для которого вычисляется скользящее среднее, должен находиться в середине периода, имеющего длину L. Если n =11, a L =5, первое скользящее среднее должно соответствовать третьему году, вто- рое — четвертому, а последнее — девятому. [1]. Тогда согласно, приведенным в таблице 3 данным и изображенным на рис. 3 зависимостям, получим сглаживание ряда методом скользящей средней (табл. 3, рис. 4).
Таблица 3 - Данные, полученные сглаживанием методом скользящей средней изменения численности персонала университета.
|
Год |
Изменения численности в % |
MA(3) |
MA(5) |
Год |
Изменения численности в % |
MA(3) |
MA(5) |
|
1991 |
14,4 |
Н/Д |
Н/Д |
1997 |
16,5 |
14 |
14 |
|
1992 |
17,2 |
15,967 |
Н/Д |
1998 |
12,9 |
14,6 |
14,4 |
|
1993 |
16,3 |
15,967 |
15,18 |
1999 |
14,4 |
14,3 |
15,76 |
|
1994 |
14,4 |
14,767 |
14,82 |
2000 |
15,6 |
16,467 |
16,12 |
|
1995 |
13,6 |
13,533 |
14,68 |
2001 |
19,4 |
17,767 |
Н/Д |
|
1996 |
12,6 |
14,233 |
14 |
2002 |
18,3 |
Н/Д |
Н/Д |
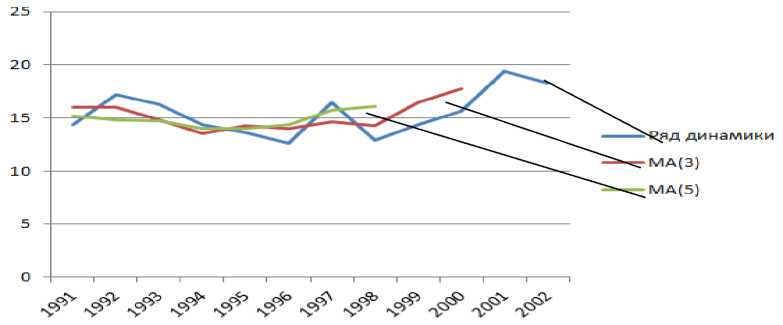
Рис.4 - Графики 3-х и 5-и летних скользящих средних
Из таблицы 3 и рисунка 4 следует, что брать больше 7-и лет скользящих средних смысла не имеет, поскольку из начала и конца этого периода выпадает большое количество значащих данных (Н/Д); это может исказить форму динамического ряда и сделать неточный прогноз [1,3].
Часто при аналитическом выравнивании ряда используется модель тренда в виде полинома. Для определения порядка аппроксимирующего полинома в этом случае и выделения тренда широко используется метод последовательных разностей членов анализируемого временного ряда. Метод основан на следующем математическом факте:
f ( t ) = a 0 + a 1 t +...+ a p t p (6)
Если временной ряд y 1 , y 2 , ..., y t , ..., y n содержит в качестве своей неслучайной составляющей алгебраический полином порядка р, то переход к последовательным разностям y(1), y (2), …, y ( n ), повторенный р +1 раз (то есть переход к последовательным разностям порядка р +1), исключает неслучайную составляющую (включая константу a 0 ), оставляя элементы, выражающиеся только через остаточную случайную компоненту u ( t ).
Алгоритм этого метода следующий: последовательно для k =1, 2… вычисляем разности Dky ( t ) ( t =1, 2…, n - k ). Из анализа поведения разностей, в зависимости от их порядка k, следует, что, начиная с некоторого k, несмотря на его дальнейший рост, разности стабилизируются, оставаясь приблизительно на одном уровне. Это значение k и будет давать порядок сглаживающего полинома, то есть p. Но следует иметь в виду при применении этого метода - стабилизация разностей не доказывает, что ряд первоначально состоял из полинома плюс случайный остаток, а только указывает на приближенное представление таким образом.
Для выявления долговременных тенденций, характеризующих изменения данных, кроме скользящих средних, применяется метод экспоненциального сглаживания. Этот метод позволяет также делать краткосрочные прогнозы (в рамках одного периода), когда наличие долговременных тенденций остается под вопросом. Благодаря этому метод экспоненциального сглаживания обладает значительным преимуществом над методом скользящих средних [1].
Метод экспоненциального сглаживания получил свое название от последовательности экспоненциально взвешенных скользящих средних. Каждое значение в этой последовательности зависит от всех предыдущих наблюдаемых значений. Еще одно преимущество метода экспоненциального сглаживания над методом скользящего среднего заключается в том, что при использовании последнего некоторые значения отбрасываются. При экспоненциальном сглаживании веса, присвоенные наблюдаемым значениям, убывают со временем, поэтому после выполнения вычислений, наиболее часто встречающиеся значения получат наибольший вес, а редкие величины — наименьший. Здесь мы сталкиваемся с большим числом вычислений, но электронный процессор Excel позволяет весьма просто и удобно реализовать метод экспоненциального сглаживания.
Уравнение, позволяющее сгладить временной ряд в пределах произвольного периода времени i , содержит три члена: текущее наблюдаемое значение Y i , принадлежащее временному ряду, предыдущее, экспоненциально сглаженное значение E i-1 и присвоенный вес W [ 1,3].
Вычисление экспоненциального сглаживания в i-м значении времени будет выглядеть следующем образом:
E i =Y i (7)
E i =WY i +(1-W)E i-1 , i=2,3,4…, n (8)
где Ei – значение экспоненциального сглаженного ряда, вычисленного для i-го периода, Ei-1 – значение экспоненциально сглаженного ряда, вычисленное для i -1 периода, Yi – значение временного ряда в i-м периоде, W – субъективный вес или сглаживающий коэффициент (0 Таблица 4 - Данные, полученные сглаживанием методом экспоненциального сглаживания изменения численности персонала университета. Год Изменения численности, в % W=0,5 W=0,25 Год Изменения численности в % W=0,5 W=0,25 1991 14,4 14,4 14,4 1997 16,5 14,55 13,575 1992 17,2 15,8 15,1 1998 12,9 14,7 15,6 1993 16,3 16,75 16,975 1999 14,4 13,65 13,275 1994 14,4 15,35 15,825 2000 15,6 15 14,7 1995 13,6 14 14,2 2001 19,4 17,5 16,55 1996 12,6 13,1 13,35 2002 18,3 18,85 19,125 Рис. 5 - Графики экспоненциального сглаживания (с коэффициентами W=0.5, W=0.25), Значение, полученное экспоненциальным сглаживанием для i-го интервала времени, можно использовать в качестве оценки предсказания значения в (i+1)-м интервале; тогда прогнозирование значений примет вид: Y+ = Е1 (9) Экспоненциальное сглаживание, как отмечено ранее, имеет преимущества перед методом скользящей средней, так как оно не отбрасывает начальные и конечные значения. Для построения диаграммы и линии тренда мы использовали стандартный программный продукт - табличный процессор MS Excel. Построение диаграммы разброса и вычисление регрессионных коэффициентов не связаны между собой, поэтому эти процедуры можно выполнять независимо друг от друга [1]. Для построения диаграммы разброса, следует выбрать команду Вставка →Диаг-рамма, затем на вкладке Вставка → Гистограмма, пункт Точечная с маркерами в раскрывающемся списке; Выберем верхнюю (первую) диаграмму, сопровождающуюся описанием: «Сравнение пар значений». Затем для вызова контекстного меню - команду «Выбрать данные…», введем в окне редактирования Выбор источника данных в поле Диапазон данных для диаграммы. установим нужные значения в Элементы легенды (Ряды), подписи и легенды к диаграмме для простоты восприятия и чтения данных. На последнем этапе построим линию тренда. Для этого выделим диаграмму, далее, вызвав контекстное меню, выбираем команду добавить линию тренда, затем выбираем необходимый вариант тренда. Заключение Выбор сглаживающего коэффициента, или веса, присвоенного членам динамического ряда, является принципиально важным, поскольку он непосредственно влияет на результат. К сожалению, этот выбор до некоторой степени субъективен. Если исследователь хочет просто исключить из временного ряда нежелательные циклические или случайные колебания, следует выбирать небольшие величины коэффициента W (близкие к нулю). С другой стороны, если временной ряд используется для прогнозирования, необходимо выбрать большой вес W (близкий к единице). В первом случае четко проявляются долговременные тенденции временного ряда; во втором случае - повышается точность краткосрочного прогнозирования [1]. Построение диаграммы и линии тренда c использованием стандартного программного продукта MS Excel, анализ временного ряда, визуализация наглядного роста или падения тенденции, весьма удобны, хотя несколько трудоемкие. Поэтому можно воспользоваться надстройкой PH Stat2 к процессору MS Excel, которая автоматически выполняет вышеописанный алгоритм.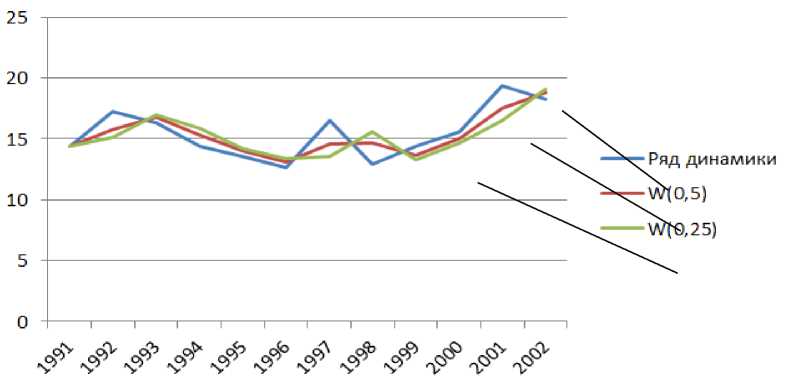
Список литературы Сглаживание трендов динамических рядов в задачах управления персоналом
- Дэвид М. Левин, Дэвид Стэфан, Тимоти С. Кребиль. Статистика для менеджеров с использованием Microsoft Excel. 4-е изд. «Вильямс». -М.: 2004. -1312 с.
- Крученецкий В.З., Айдауова А.А., Заурбеков Н.С. К использованию стандартных компьютерных средств в менеджменте персона-лом ВУЗа. ∕∕ Материалы VIII международной конференции «Инновационная политика и устойчивое развитие современного общества», Казахстанско-Немецкий Университет (КНУ), 17 марта 2016г., Алматы. -С.186-191.
- Крученецкий В.З., Калабина А.А. и др. Некоторые аспекты прогнозирования бизнес-процессов с использованием методов анализа времен-ных рядов и стандартных программных средств.//Вестник АТУ. -№ 5 (101). -2013. -С 39-46.


