Сходимость рядов Вольтерры при анализе нелинейных динамических схем

В настоящее время центр тяжести научных исследований переместился в моделирование. Новые математические формулировки и алгоритмы естественным образом приводят к изменению и развитию устоявшихся представлений, способствуя удачному решению научно-технических задач.

Для частотного анализа нелинейных схем обычно привлекается или метод гармонического баланса, или метод рядов Вольтерры [1; 2]. Каждый из подходов имеет свои многочисленные проблемные стороны и нуждается в дальнейшем развитии. То, что широкий класс физических и биологических систем описывается функциональными рядами Вольтерры известно достаточно давно. На начальном этапе поиска новых идей для оптимизации характеристик нелинейных устройств функциональные ряды, имеющие ярко выраженное физическое содержание, представляются более полезными, чем процедуры с абсолютной формализацией реальных процессов. Однако практическое применение этого мощного инструмента за рамками слабо нелинейного взаимодействия сдерживается серьезными проблемами, в первую очередь связанными со сходимостью функциональных рядов.

В [3–5] показано, что расходимость функциональных рядов возникает в том случае, если

Вольтерры.

в схеме начинают лавинообразно нарастать повторные взаимодействия вида p (m 1Ю1 + Hi®2 + ...) + q (m2®1 + тг2®2 + ^) + ^, обусловленные петлями скрытых или явных обратных связей, неизбежно присутствующих в схеме. Если уровень продуктов повторного нелинейного взаимодействия, циркулирующих по контурам схемы, начинает превышать некоторое критическое значение, то сильно нелинейный анализ на платформе функциональных рядов становится не только непрактичным, но и принципиально невозможным. Классические ряды Вольтерры не справляются с такого рода нелинейными задачами, т. к. концепция разделения составляющих по уровням нелинейности становится неработоспособной. Способность разделять составляющие по уровням нелинейности, органически присущая рядам Вольтерры, одновременно является и самой сильной, и самой уязвимой стороной, обусловливающей низкую устойчивость рекурсивного вычислительного процесса.

Итак, универсальная причина расходимости рядов Вольтерры – это проявление деструктивного характера влияния внешних или внутренних обратных связей на концепцию разделения продуктов по уровням нелинейности. В данной работе углубляются и детализируются общие © А.М. Бобрешов, Н.Н. Мымрикова, 2014

представления о закономерностях, сопровожда- ющих срыв итерационного процесса нахождения решения с помощью функциональных рядов. При этом показывается, какие именно скрытые особенности в точном решении приводят к появлению критических для рядов Вольтерры точек при отсутствии видимых аномалий во внешнем поведении нелинейной системы.

Следует отметить, что сумма Вольтерры tt

^J —Jk (ti, —,т n) E (t-т1) — n=10    0

операторов

— E (t - т n) d T1 — d т n или является точной моделью аналитической нелинейной системы с внутренней структурой, или используется как приближенный инструмент функционального регрессионного ана- лиза неаналитических поведенческих систем. В первом варианте ряды Вольтерры при учете необходимого числа ядер либо точно описывают нелинейные процессы, либо резко расходятся, не справляясь с описанием высокого уровня повторных взаимодействий в петлях обратных связей. Во втором варианте ряды Вольтерры – это функционально-полиномиальная регрессия для хранения дискретной информации о поведении нелинейной динамической системы в проведенных над ней экспериментах. В дальнейшем речь будет идти о сходимости аналитических рядов Вольтерры с увеличением порядка учитываемых ядер, определяемым по исходным дифференциальным уравнениями и ассоциируемым системам линейных алгебраических уравнений. ×то касается функционально-полиномиальной регрессии, то более или менее надежно можно идентифицировать только ядра 1–3-го порядка, а сходимость рядов понимается совсем в другом смысле (как повторяемость результатов при увеличении числа временных отсчетов для характеристик «вход-выход»).

Поскольку ряды Вольтерры начинают расходиться в точках, за которыми аналитическое продолжение решения в комплексную область перестает существовать в виде степенного ряда с положительными степенями [4; 5], то к реальному воздействию на входе рассматриваемой системы следует добавить мнимую часть. Далее все возможные решения для отклика нелинейной системы должны быть получены в комплексной форме. Однако в общем случае найти аналитическое решение нелинейных алгебраических уравнений выше четвертого порядка нельзя.

×то касается нелинейных дифференциальных уравнений, то даже для самых простых нелинейных схем с гармоническим воздействием аналитическое решение в общем случае отсутствует. В связи с этим для нахождения полного набора возможных откликов системы искомое решение представлялось в виде гармонического ряда да

u ( t ) =

^ U h exp ( jh to t ) , h =-да

а коэффициенты ряда Uh определялись из системы нелинейных алгебраических уравнений. По существу, это гармонический баланс. В отличие от метода гармонического баланса, используемого в системе AWRMWO, для системы нелинейных уравнений n-го порядка необходимо обеспечить нахождениеnрешений, включая комплексно-сопряженные. Для этой цели эффективным оказался подход, развитый в [3; 6]. Для этого подхода характерен полный отказ от концепции разделения динамики по уровням нелинейности и переход к унифицированным матричным операциям, сводящимся преимущественно к рутинной многократно повторяющей- ся процедуре умножения матриц на векторы напряжений. Подход также хорошо приспособлен к работе с комплексными переменными. Кроме того, в отличие от традиционного гармонического баланса, в нем спектральные преобразования осуществляются бездискретного преобразования Фурье, что способствует улучшению точности результатов. Поскольку для решения поставленной задачи вычислительная схема должна обладать очень высокой устойчивостью, то все-таки пришлось внести некоторые изменения: метод итераций Пикара заменен методом Ньютона – Рафсона. В результате методика матричного анализа оказалась менее чувствительной к рекурсивности описания нелинейных взаимодействий и позволила найти все требуемые решения. Поскольку характеристики нелинейных элементов задаются степенными полиномами и легко дифференцируются, то вычисление якобиана почти не усложняет теорию. В частности, для одноконтурной нелинейной схемы c уравнением (3) или (4)

Gu + g ( u ) = E , g ( u ) = a 1 u + a 2 u ² + a 3 u ³ + — (3)

du

C --+ g (u ) = E , dt ⁽ )

E = E o cos to t

соответственно решаются уравнения (5) или (6) для ( k + 1 ) -й итерации вектор-столбцов напряжений U ^{( + 1 )}

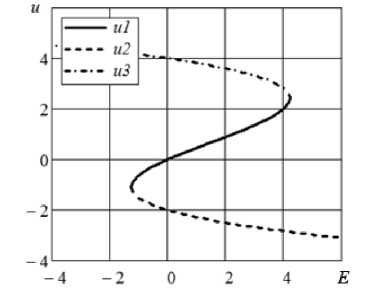
Рис. 1. Вещественные решения нелинейного уравнения (3): а ) a 3 / a 2 =

- 0.5; б ) a 3 / a 2 = + 0.5

( G + a 1 + 2 a ₂ U ⁽ k ) + 3 a ₃ U ⁽ k ) ² + _ ) U ⁽ k ^{+ 1 )} = = ( a ₂ + 2 a ₃ U ⁽ k ) + _ ) U ⁽ k ) U ⁽ k ) + GE, ( j®C + a 1 + 2 a ₂ U ⁽ k ) + ...) U ⁽ k ^{+ 1 )} = = ( a ₂ + 2 a ₃ U ⁽ k ) + _ ) U ⁽ k ) U ⁽ k ) + jrnCE

Вектор-столбец U

( k )

и матрица напряжений

U ⁽ k )

формируются из напряжений на ( k )-й итерации

Г ... ^

( k ) 2

U ₁ ( k )

U ⁽ k ) =

( k ) 0

U ( k

U

( k )

- 2

r...

( k )

□

( k ) U ₀

U - ^k 1)

( k )

^U - 2

( k )

^U - 3

(k)(

U ₁ U ₂

U 0 ^k ) U 1k )

(k)(

^U - 1 ^U 0

(k)(

^U - 2 ^U - 1

......)

U 3k)

U (k)

U k)

U ')

– диагональная матрица частот; E – вектор

входного воздействия [3; 6].

Рис. 1, à иллюстрирует возможные решения уравнения (3) и системы уравнений (5) в зависимости от значения напряжения E на входе (с трехчленным полиномом при соотношении между коэффициентами a 3 / a 2 = - 0.5). Видно, что в диапазоне значений E от –1.262 до 4.225 уравнение (3) имеет три вещественных корня u ₁, u 2 , u з . Один из корней U i при E = 0 имеет нуле

вое значение, остальные два корня U 2 , и 3 отличны от нуля даже в отсутствии воздействия. Ряды Вольтерры позволяют найти только корень u ₁, проходящий через начало координат. При уче-

те достаточного числа ядер результаты, полученные с помощью рядов Вольтерры и тестовые расчеты, совпадают до 5–6 знаков после десятичной точки. В точке E = - 1.262 два корня U i , и 2 стягиваются в одну точку, а в точке E = 4.225 становятся равными U i и U 3 . Вне этого интервала корни U i , U 2 ( E <  - 1.262) и U i , U 3 ( E >  4.225) перестают существовать в вещественной форме (приобретают комплексные значения). Левее E = - 1.262 вещественным является корень U 3 , правее E = 4.225 — корень U 2 . Однако метод рядов Вольтерры не позволяют найти эти корни, и вне диапазона - 1.262 .„ + 4.225 функциональный ряд расходится.

При воздействии на входе гармонического сигнала с амплитудой E ₀ мгновенное значение напряжения будет изменяться в диапазоне от - E 0 до + E 0 . Поэтому при выбранных значениях коэффициентов a_i радиус сходимости рядов Воль-терры будет 1.262. На рис. 2, à приведены временные зависимости напряжения при E ₀ = 0.5. Наблюдается три возможных временных процесса U i ( t ), U 2 ( t ), U 3 ( t ). С помощью рядов Воль-терры может быть рассчитано только колебание u ₁( t ), изображенное сплошной линией. По мере увеличения входного воздействия две кривые u ₁( t ), u ₂( t ) начинают все больше сближаться, при этом сходимость рядов Вольтерры при расчете зависимости u ₁( t ) все более замедляется. При E 0 = 1.262 минимумы кривой U i ( t ) и максимумы кривой u ₂( t ) начинают соприкасаться (рис. 2, á ). Ýтот случай является критическим для рядов Вольтерры. При дальнейшем увеличении E ₀ на вещественной плоскости остается только одна кривая U 3 ( t ). Однако эту зависимость уже нельзя рассчитать рядами Вольтерры. Вначале ряды Вольтерры начинают расходиться очень медленно, поэтому для надежной идентификации критической точки в функциональных рядах удерживалось до ста членов.

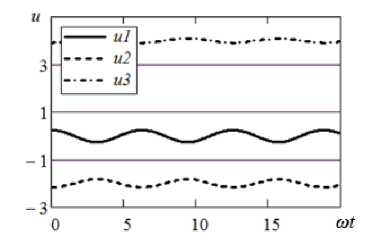
Рис. 2. Временные процессы в нелинейном резистивном контуре при гармоническом воздействии E о cos ш t : а ) E о = 0.5; б ) E ₀ = 1.262

Отметим, что метод гармонического баланса тоже «чувствует» приближение критической точки, после которой происходит перекрытие двух из трех вещественных решений. Так как система на некоторую часть периода скачкообразно переходит в другое состояние, то это сопровождается резким возрастанием неустойчивости итерационного процесса. Например, если в качестве критерия окончания итерационного процесса задать отличие амплитуд последовательно найденных гармоник менее чем на 10 - ⁵, то решение уравнения с линейным начальным приближением при прохождении критической точки 1.262 не будет найдено даже за 1000 итераций, в то время как при меньших значениях E ₀ нужно всего максимум 5–7 итераций. Усложняется спектральный состав выходного колебания (рис. 3). Наличие в спектре заметных гармоник выше третьего порядка свидетельствует о сильном повторном взаимодействии гармоник, т. к. степень аппроксимирующего нелинейность полинома равна трем.

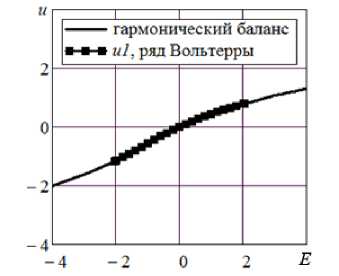
При изменении знака коэффициента a ₃ на противоположный ( a 3 / a 2 = + 0.5) уравнение (2) и система (4) при любых значениях Å имеют единственный вещественный корень и два комплексно-сопряженных корня (не имеющих физического смысла). Однако радиус сходимости ряда Вольтерры все равно становится конечным, и в этом случае диапазон сходимости - 2.0367... + 2.0367 (рис. 1, б ). Объяснение следует искать в теории функции комплексной переменной. Если реальное воздействие дополнить мнимой частью и найти решение на комплексной плоскости, то в этой особой точке тоже будет происходить ветвление корней. В соответствии с теорией функции комплексной переменной за радиусом окружности, проходящей через точку ветвления, разложение функции в ряд по положительным степеням становится невозможным [7]. В результате ряды Вольтерры начинают расходиться. Отметим, что на эту критическую

Рис. 3. Амплитудыгармонических составляющих отклика точку реагируют только ряды Вольтерры, не справляясь с «проклятием размерности» из-за чрезмерных повторных комбинационных взаимодействий. Метод гармонического баланса в данной ситуации не обнаруживает замедления сходимости итерационного процесса.

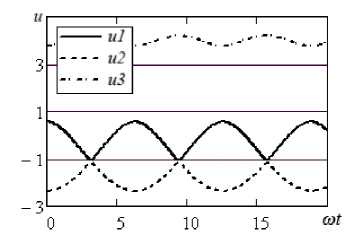
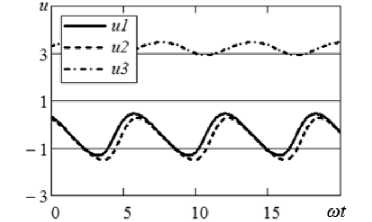
На рис. 4, à показаны три возможных решения дифференциального уравнения (4) и системы уравнений (6) при a 3 / a 2 = - 0.5; Е 0 = 0.5; to С = 1. И в данном случае может существовать три временных процесса u ₁( t ), u ₂( t ), u ₃( t ) при одном и том же гармоническом воздействии. На графике сплошной линией выделен отклик системы, который определяется с помощью рядов Вольтерры. На рис. 4 переходные процессы не показаны, т. к. метод гармонического баланса позволяет найти только установившуюся часть решения (4). По мере увеличения Å ₀ два решения u ₁( t ), u ₂( t ) начинают все больше сближаться (рис. 4, б , Е 0 = 1). Для Е 0 = 1.00576 кривые ^ 1 ( t ), u ₂ ( t ) полностью сливаются. При дальнейшем увеличении Å ₀ решения u ₁( t ), u ₂( t ) перестают существовать в вещественной форме, и остается только одна зависимость u ₃( t ), которая не может быть рассчитана с помощью функциональных рядов. Ситуация с наложением решений соответствует предельным возможностям этого аппарата, и Е 0 = 1.00576 — это радиус сходимости ряда Вольтерры при заданных параметрах нелинейной системы.

Случай a 3 / a 2 = + 0.5 для динамической схемы аналогичен тому, что имело место для резистивной схемы (см. рис. 2, á ). Имеется одно ве-

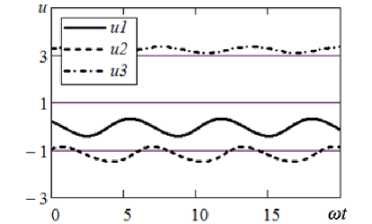
Рис. 4. Временные процессы внелинейном RC -контуре при гармоническом воздействии E 0 cos ш t : а ) E 0 = 0.5; б ) E 0 = 1

щественное решение дифференциального уравнения u ₁( t ) и пара комплексно-сопряженных решений u ₂( t ), u ₃ ( t ). Место ветвления решений на комплексной плоскости как раз соответствует критической для рядов Вольтерры точке.

Для резистивной и динамической схемы величины G и ш С были взяты равными, но радиус сходимости для динамической схемы оказался несколько ниже в обоих случаях. Вообще говоря, для сложной схемы (с несколькими контурами обратной связи) затруднительно априорно предсказать, как сильно изменится радиус сходимости при переходе от резистивной схемы к динамической, т. к. действует несколько конкурирующих факторов. Во-первых, в отличие от резистивной схемы, проводимости емкостей для частот высших гармонических составляющих не одинаковы, и величина htoC тем больше, чем выше номер гармоники h (для индуктивностей, наоборот). В зависимости от топологии схемы это может привести как к повышению, так и понижению уровня повторных взаимодействий. Во-вторых, если в резистивной схеме были контуры с положительной обратной связью, то при переходе к динамической схеме продукты повторного взаимодействия уже не будут синфазны продуктам первичного взаимодействия, и нелинейное взаимодействие ослабится. В-третьих, при наличии контуров с отрицательной обратной связью при переходе к динамической схеме продукты первичного и повторного взаимодействия будут взаимно компенсироваться в меньшей степени, т. к. они не останутся строго противофазными; в результате нелинейное взаимодействие усилится. Проведенная серия расчетов это подтверждает.

Таким образом, охватывающая нелинейные элементы глубокая обратная связь, интенсивные повторные комбинационные взаимодействия спектральных составляющих, точки ветвления решений на комплексной области, разрушение концепции разделения взаимодействий по уровням нелинейности и конечный радиус сходимо- сти функциональных рядов – все это различная физическая или математическая интерпретация закономерностей поведения моделей нелинейных динамических систем. По существу, критические для сходимости рядов Вольтерры уровни воздействия – это точки явного или скрытого перехода модели нелинейной системы из одного состояния в другое. И ряды Вольтерры с их слабой рекурсивной устойчивостью являются как бы индикатором такого перехода системы (в том числе перехода, не заметного по внешним характеристикам) в состояние, когда разделение продуктов взаимодействия по уровням нелинейности оказывается невозможным.