Simulation of relay-races

Multistage concurrent games, in which situation develops in physical time, or relayraces objectively exist in different fields of human activity, such as sport, economics, politics, defense etc. [1-4]. In games of this type "distance" that should be overcome by participants is broken down into "stages", and efficiency of "distance" passage depends not only on overall "winning" the whole "distance", but also on "winning" the "stages" (below terms "distance", "stage", "winning", "forfeit" etc. will be used without inverted commas).

In the paper assumptions are as follows [5]:

• 1)    relay-race is considered as passing by participants of equal distance in real physical time;

• 2)    distance of every participant is divided onto stages, every of which has a number equal for all participants;

• 3)    stages with the same numbers have equal length;

• 4)    all participants start at once;

• 5)    time of passing of every stage by the participant is a random one and is de-fined individually for him with accuracy to density;

• 6)    after completion of a current stage the participant starts the next one without a lag;

• 7)    winning or losing of a stage competition is understood as completion of the stage being the first or not the first;

• 8)    winner’s forfeit is distributed in time and depends on difference of stages, which winner and losers pass.

• 1.    Relay-Race as М-Parallel Semi-Markov Process

Distance, stages and participants are shown on Fig. 1, where the following indexes are used: 1 < m, n < M are numbers of participants under competition; 0 < i, j < J are numbers of stages, or numbers of changeover points. Point 0 is the start one, point J is the final one. Number of stage is cpiite similar with number of starting points. Indexes of stages are performed as functions. Bracketed part of index are points of participants.

* 1 2 ... m ... v: M	0(1)		i (1)	...	J (1)-1	J (1)
	0(2)		i (2)	...	J (2)-1	J (2)
	0( m )	...	i ( m )	...	J ( m )-1	J ( m )
	0( M )	...	i ( M )	...	J ( M )-1	J ( M )
	0       1	...	i     i +	... J -1     J

Stage’s Number

Fig. 1. Distances, stages and participants of relay-race

Model of relay-race with M participants may be performed as M-parallel semi-Markov process h (t) = [ h i( t) ,...,hm (t) ,...,hn (t),... hM (t)],                        (1)

where t is the time: h m ( t ) is the m -th semi-Markov nratrix [6. J of size ( J + 1) x ( J + 1). which describes passing the stages of distance by m -th participant;

h m ⁽ t ) — Vhj ( m ) ,l ( m )⁽ t ) J,                                        (-)

h        ₍ t ) = / fi ( m )⁽ t ) , when ^{/ (} m ^)— j ⁽ m ^{) + 1} ,

j ⁽ m ) ,l ⁽ m )(         о , ^ _ац _other cases.

fi ( m )( t ) is density of tinie of passing the Ftli stage by the m -tli participant. For densities fi ( _m )( t ) the following restrictions are performed:

∞ j tfi(m)(t)dt < ^ ^hen 0 < i (m) < J, 1 < m < M, 0

fj(m)(t) = lim §(t - т), 1 < m < M, τ→∞ where §(t — т) is a, shifted Dirac 5-function.

The first restriction means that all participants pass all stages, except the J -th, during a finite time. The second restriction means that the J -th stage may be considered as stage with infinite time of passing.

Numbers of stages may be performed as the cortege p — (0 ,... ,i,..., J ), the M -th Cartesian degree of which gives an M -dimensional space s — p^M of states of process (1) (Fig. 2). Coordinates of space are fixed on the participants, discrete coordinate values define numbers of changeover points, or current stages of participants. In the space s an M -dimensional vector of states is defined

S = [г(1),...,г(т),...,г(М)], where i ( m ) is the number of a current stage of the m-th participant.

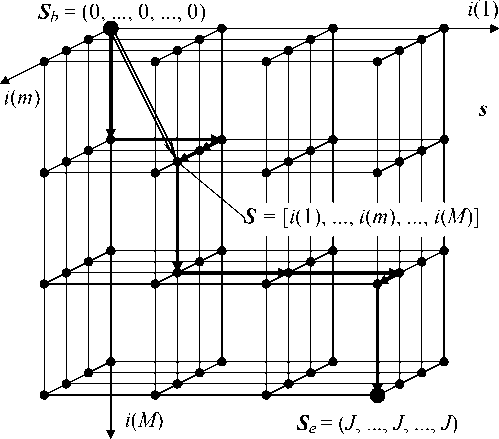
Fig. 2. Space s of states

The total number of states is equal to ( J + 1) M. Initial meaning of vector S b = (0 ,..., 0 ,..., 0). Wandering through M -parallel semi-Markov process has the character of evolution, in which after every switch some element of vector S increments by a unit. For any switches incremental element is the only one. Switches last till state S e = ( J,..., J,..., J ). The total number of switches during evolution is R = JM.

• 2.    Common Formulae for Evolution Parameters

During evolution the ordinary semi-Markov processes, described by (1), compete between them [2,5]. Let us consider the common case, when processes under competition are described with densities 9 1( t ) ,..., 9 _a ( t ) ,..., 9 A ( t ). In such a case density of time till a first switching is defined as

A  AA

9w ( t ) = ^9wa ( t ) =     9a ( T ) П [1 - 6 в ( t )] ,

a =1           a =1        в =1

в=a where 9wa(t) is the weighted density of time of winning the a-th density: 6в(t) = ft 9в(т)dT is distribution function.

The probability of win of the а -th density and pure density of time of winning the а -th density are, correspondingly, equal to:

πwα

∞

⁹ wa ⁽ t ) ^dt ;

φwα

9 _wa ( t ) ⁿ wa ⁽ t )

The following proposition is quite correct.

Proposition 1. If density 9a(t) is under restriction (3), i.e. 9a(t) = limт,.x 5(t — т), then nwa = 0.

Really, in this case

∞A

A

= lim n i¹ - ⁶ в ^{( т )]} • τ →∞

β =1

β ̸ = α

nwa = / lim 5 ( t — т ) П [1 - 6 в ( t )] dt τ →∞

β =1

⁰                 β ̸ = α

If among the functions 6 в ( t ) there are functions, for which 6 в ( t ) = lim _тx^ n ( t - т ), where n ( t — т ) is shifted Heaviside function, then one can always demand the solution of indeterminacy as lim _т ,. _x. J^ 5 ( t — т ) n ( t — т ) dt = 0. So, proposition 1 may be considered to be proven.

The second formula, necessary for relay-races simulation, is the dependence for waiting time density. If from competing processes of 9 _a ( t ) and 9в ( t ) , 9в ( t ) ^wi^ns the process, it waits until 9 _a ( t ) will be completed, which may be evaluated as [2,5]

n ( t ) f 9в ( e ) 9a ( t + e ) de

9 •■ ( t ) = ----- ^----------------------

f 6 в ( t ) d 6 a ( t )

Proposition 2. If 9_a ( t ) is restricted by (3), then the lower boundary of the domain and expectation of 9в^_а ( t ) tend to infinity.

∞

Really, in that case denominator of (7) is equal to J 6 в ( t ) lim _т^^ 5 ( t — т ) dt = 1. Lower 0

boundary of 9в(t) is min {агд^9в(t) > 0J} = Tвmin > 0. So lower boundary of numerator of ( ?) is min arg J 6в (e) limт .. 5(t — т + e)d( > 0 = limт.. (Тв min + т) ^ го.

It is known [8], that for every random value expectation ranges in domain T min <  T < T max, where T is an expectation, T _min , T max are lower and upper boundaries of domain. Consequently, if Tв _min ^ го , then Tв ^ го , where Tв = J^ t9в ( t ) dt is an expectation of time of completion 9в ( t ).

So, proposition 2 may be considered to be proven.

Proposition 3. If lower boundary of density 9_a ( t ) is as T_{a min} ^ го, then

π _wα

∞A

= / 9a ( t ) П [1

β =1

⁰        β ̸ = α

— 6 в ( t )] dt = 0 •

Really, density 9 _a ( t ) may be performed as a result of ideal multiplicative sampling with the infinitesimal sampling period:

∞

9a ( t )= lim E 9a ( t ) 5 ( t — Zl ) ,                            (8)

ζ →∞ _{l =0}

where Z ^ го is the sampling period.

All readouts of function (8) belong to t > T _{a min} ^ to, thus

∞

9a ( t ) —   lim lim ^ 9a ( t ) 5 ( t - Ta min - Zl ) •

T a min '^ Z '^ j=J

So, according to proposition 1,

∞

— ^z l ) П^[1 - ⁰ в ⁽ t ^)] dt ^{— 0} , в =1 в = a

ⁿ wa —

lim lim ^ 9 a ( t ) 5 ( t — Ta min

J  T a min '^ Z '^ ²=0

and proposition 3 is proved.

Proposition 4. If density distribution 9_a ( t ) has the property min arg 9_a ( t ) — T_{a min} ^ to, then lower boundary of domain and mathematical expectation of 9p_ia ( t ) tend to infinity.

Really, in accordance with intermediate result of proposition 2, in this case the de-∞∞ nominator of (7) J 0в(t) lim lim   9a(t)5(t — Tamin — Zl)dt — 1- Lower boundary of

0         T a min '^ ^Z '^ l =0

numerator of (7) in this case

∞∞ min arg / 9 в (f)   lim   lim ^^ 9a (t) 5 (t — Ta min

— Zl ) d( >  0 — Ta min ^ TO,

0       Ta min'^ Z '^ ^=J and proposition 4 is proved.

With use of dependences obtained and propositions proved a recursive procedure of relay-race evolution analysis may be formed.

• 3.    Recursive Procedure of Relay-Race Evolution Analysis

Evolution of relay-race develops as competition in M -parallel semi-Markov process [912]. Let us introduce the concept of switching trajectory in the space s of states (Fig. 2) as the realization of stochastic sequence of vector S from state S b till state S _e. The trajectory as a whole is occasional, the realization is quite deterministic for every concrete case of evolution [6,8].

Let us consider some (f.e. fc -th) case of evolution, which starts from state S b — (0 , • • •, 0 , • • •, 0). When no switches took place, the total number of switches is equal to r — 0, and participants pass zero stages of their distances. Initial densities from zero rows of matrices h_m ( t ) , 1 < m < M participate in competition.

Let the n -th participant win in the fc -th realization under consideration. Probability of his winning may be obtained from (5) [13]:

∞M n0,k — / 0g0(n) (t) П [1 - 0GJ(j)(t)] dt,                        ^

0                 j =1, j=n

∞ where   '"G...(t) — Jgg.„(т)dx is the distribution function; 0g0(j)(t) — f0(j)(t),

0(1) < 0(j) < 0(M), upper left index points to the number of previous switches; lower right index points to the number of stage, in which the j-th participant stays in current moment of time.

Density of time spent by the winner for passing zero stage is equal to (5)

M

⁰ 9 0( n )⁽ t ) П [1 ^- ° G 0( j )⁽ t )] j =1 , ^j =n

Ф ° ,k = ---------------------------- П ° ,k

After winning of the n -th participant on the zero stage he begins to pass the first stage, although all others continue passing their zero stages. This is why after the first switch the following densities participate in the competition:

gi ( j )⁽ t )

g °( n ) ^ °( j )( t ) , when j = n, f 1( n )( t ) ,       when j = n,

(П)

where g °( _n ) ^ °( j )( t ) is the density of waiting time for tire n -tli participant until the j -tli participant completes his zero stage.

Lower right indexes of ¹ gi ( j )( t ) in the switching trajectory realization are as follows:

i (1) = 0 ,..., i ( m ) = 0 ,..., i ( n ) = 1 ,... i ( M ) = 0 .

Let us analyze the situation after r switches of the fc -th realization. In accordance to conditions of evolution total number of switches is equal to

M

^ i ⁽ j ) = r, j =1

where i (1) ,..., i ( m ) ,..., i ( n ) ,..., i ( M ) are different, in common case, nominations of indexes, which define numbers of stages, passed by participants in the fc -th realization after r switches.

Let us denote the densities, which participate in competition after r switches, as ^r gi (i)( t ) , ..., ^r gi ( _m )( t ) , ..., ^r gi ( _m )( t ) , ..., ^r gi ( _M )( t ). and suppose. that the Z -tli participant wins.

The probability of his winning is equal to

∞M nr,k = / r gi (l)(t) П [1 ~ rGi(j)(t)] dt,

°                j ==1, j =l where rgi(j)(t) are densities, which participate in competition after r switches.

In particular, if after r switches in the fc -th realization the first participant wins, then the probability of his winning is equal to

∞M nr,k = /rgi(i)(t) П [1 - rGi(j)(t)] dt.

°            j=1, j =1

Density of between switches in a general case is equal to фг,к

M rgi(i)(t) П [1 j=1, j =l

-

r Gi ( j )( t )]

.

πr,k

Let us note, that after J switches in M cases from the MJ realization, there emerges a situation, when vector S takes one of the next nominations: ( J, 0 ,..., 0 ,..., 0) ,..., (0 ,..., 0 , J, 0 ,..., 0) ,..., (0 ,..., 0 ,..., 0 , J Y After that quantity of possible competition outcomes from denominated sates decreases to unit. If the m -th participant gets the state J , then the probability of outcome from this state, according to propositions 1 and 3 is equal to zero.

After winning of the Z -tli participant for the r -th switching, he starts the [ i ( Z ) + 1]-th stage of his distance. All other participants continue the i ( j )-th stage, 1 < j < M,j _ Z. This is why in competition for the ( r + 1)-th switching the next densities participate:

r+П, ,(о -1 rgi< 1)^(j>(t)■ "lien j _ l, gi1 j)(t)     I fi(i)+i(t),      when j' = Z, where gi(l).,(j)(t) is the waiting time (7).

In particular, if in the fc -th realization the first participant wins, for ( r + 1)-th switching the next densities contend:

r +1 , . _{( t} ) _ { rgi (1) ^ i ( j )⁽ t ) , when j = ¹ , i ⁽ j )        \fi (i)+i( t ) ,      when j = 1 .

And lastly, let us assume, that in the fc -th realization after the ( R — 1)-th switching the state

\ J,      when I ^{_ m} ,                 i

i ⁽ l ^)_t J — 1 , when / _ m,  \ i ⁽ l ^)_ R ^{— 1}

emerges.

Probability of winning of the m -th participant is as follows:

^П R — 1 ,k

∞M

_ / R-1 gj(m)-1(t) П [1 — о                j-• j=m

R ¹ Gj ( i )( t )] dt.

Due to propositions 1 and 3, n _{R- 1} , _k _ 1. Probabilities of winning of all other participants (they reach the states J ) are equal to zeros. Densities of residence in states after R switchers are as follows:

,      _ J Rgj ( m ) - 1 ^ J ( i )( t ) , when j _ Z _ m ;

'gi ⁽ j ⁾⁽ t )     1               ^f J ( j )⁽ t ) , j ^_ l ^{_ m} .

Results of the fc -th recursive procedure are shown in Table 1.

The probability of the fc -th realization of evolution and the time density for finishing of the fc -th realization of relay-race are as follows:

R - 1

Пк _ П Пк,г, r =0

R - 1

Фк ( t ) _ L ^{- 1} П L [ фк, ( t )] , r =0

Table 1

fc -th recursive procedure

r S Densities 0 0,..., ,..., 0,..., 0 f0(1), . . . , f0(m), . . . , f0(n), . . . , f0(M) g0(1), . . . , g0(m), . . . , g0(n), . . . , g0(M) 1 0, . . . , 0, . . . , 1, . . . , 0 g0(n)^0(1), . . . , g0(n)^0(m), . . . , f1(n), . . . , g0(n)^0(M) g0(1), . . . , g0(m), . . . , g 1(n), . . . , g0(M) 2 0,...,1,...,1,...,0 g0(m)^0(1), ..., f1(m), . . ., g0(m)^ 1(n), . .., g0(m)^0(M) g0(1), . . . , g 1(m), . . . , g 1(n), . . . , g0(M) 3 0,..., 1,...,2,...,0 g 1(n)^0(1), . . . , g 1(n)^ 1(m), . . . , f2(n), . . . , g2(n)^0(M) g0(1), . . . , g 1(m), . . . , g 1(n), . . . , g0(M) 4 0,..., 1,...,3,...,0 g2(n)^0(1), . . . , g2(n)^ 1(m), . . . , f3(n), • • • , g2(n)^0(M) g0(1), . . . , g 1(m), . . . , g3(n), . . . , g0(M) ■ ■ ■ III • •• r i(1),..., i(m),..., i (n),..., i (M) • •• r gi (1),...,r gi (m),...,r gi (n),...,r gi ( m ) r + 1 i (1) + 1,... ,i (m), ..., i (n),..., i (M) fi (1)+1, . . . , gi (1) ^i (m), . . . , gi (1) ^i (n), . . . , gi (1) ^i (M) r+1 gi (1), . . . , r+1 gi (m), . . . , r+1 gi (n), . . . , r+1 gi (M) ■ ■ ■ III III R - 2 J(1),...,J(m) - 1 J(n),...,J(M) - 1 III R—2 gJ (1),. . . , R—2 gJ (m) -1, ..., R—2 gj (n),. . . , R-2 gj (M) -1 R-1 J (1),..., J (m) — 1 J (n),..., J (M) R—2 gj (M)-1 ^J (1), . . . , R—2 gj (M)-1 ^J (m) -1, . . . , R-2 gJ (M) -1 ^J (n) . . . , fJ (M) gJ(1), . . . ,       gJ (m) -1, . . . ,       gJ (n), . . . ,       gJ (M) R J (1),..., J (m),..., J (n) ,...,J (M) R-1                              R-1 gJ (M) -1 ^J (1), . . . , fJ (M) . . . ,      gJ (m) -1 ^J (n), . . . , R-1 gJ (m) -1 ^J (M) gJ(1), . . . ,   gJ (m), . . . , gJ(n), . . . ,   gJ(M) where L [...] and L1 [...] are the direct and the inverse Laplace transforms correspondingly. Total quantity of realization K grows fast in dependence on number of participants and number of stages (R. Bellman’s "curse of dimensionality" [1]). The growth of realizations quantity is restricted by the fact that during switches some participants get the J-th stage and further evolution on this branch is impossible. So it born difficulty of calculation of total quantity of realizations.

• 4.    Evaluation of Effectiveness of Relay-Race Strategy

It is quite natural for evaluation of effectiveness to use the model, in which

• •    the pairs of part.icipants. f.e. the m -th and the n -th are considered:

• •    participant, who gets a stage with higher number, acquires a forfeit from participants, who get a stage with lower number;

0 ... 0

е forfeit is defined as a distributed payment ci ( _m ) ,i ( _n ) ( t ), value of which depends on time.

Elements    ci ( _m ) ,i ( _n )( t )   are stacked into four-dimensional matrix of size

( J + 1) X ( J + 1) X M X M:

e( t ) — [ e mn ( t ) J, 1 < m,n < M.                        (19)

where e _m , _n ( t ) is a symmetrical matrix of size ( J + 1) X ( J + 1), which characterizes payments of the m -th participant to the n -tlr one:

	c 0( m ) , 0( n )( t )    .	.     c 0( m ) ,i ( n )( t )     .	■ c 0( m ) ,j ( n )( t )
c m,n ( t )	ci ( m ) , 0( n )( t )     .	... . ci ( m ) ,i ( n )( t ) .	.   ci ( m ) ,j ( n )( t )	;             (20)
	cj ( m ) , 0( n )( t )    .	... . cJ ( m ) ,i ( n )( t ) .	. cj ( m ) ,j ( n )( t )

Cm,n ( t ) =        ...      , 1 < m < M.

0 ... 0

Let us extract from the general fc -th realization only participants m and n and tabulate the к ₂ , _m , _n -th realization of pair evolution.

к ₂ , _m , _n -th realization of pair evolution

r	S	Densities
0	0 , 0	f 0( m ) , f 0( n ) , 0 g 0( m ) , 0 g 0( n )
1	0 , 1	g 0( n ) ^ 0( m ) , f 1( n ) , g 0( m ) , g 1( n )
2	1 , 1	f 1( m ) , g 0( m ) ^ 1( n )
		• I I
r	i ( m ) , i ( n )	g i ( m ) , g i ( n )

Table 2

r	S	Densities
r + 1	i ( m ) + 1 , i ( n )	f i ( m )+1 ,     g i ( m ) ^ i ( n ) r +1 gi ( m )+1 ,r +1 gi ( n )
		.  •   •
R - 2	J ( m ) — 1 , J ( n ) — 1	R - 2 gj ( m ) - 1 ,R - 2 gj ( n ) - 1
R - 1	J ( m ) — 1 , J ( n )	R - 2 g J ( m ) - 1 ^ J ( n ) - 1 , fj ( n ) R - 1 gj ( m ) - 1 ,R - 1 gj ( n )
R	J ( m ) , J ( n )	f     R- 1 „ fj ( m ) ,      g j ( n ) ^ j ( m ) - 1

Analysis of evolution shows that situation, which changes conditions of forfeit payments, emerges from the winning of one of the participants and lasts till the next switching. If after r switches densities ^r gi ( _m )( t ) and ^r gi ( _n )( t ) compete, then the entire sum of forfeit on the stage is as follows [2]:

∞ r,k2 ,m,n

Cm,n —

{ r ^g i ( m )( t ) [1 ^— Gi ( n )( t )] + r ^g i ( n )( t ) [1 ^— Gi ( m )( t )] } ci ( m ) i ( n ) dt      (21)

Due to (21) the n-tli participant pays to the m-tlr. if i(m) > i(n). and the m-tlr participant pays to the n-th, if i(m) < i(n). For the к2,m,n-th realization of relay-race on formulae, obtained from (5), the probabilities nr,k2mn corresponding to concrete order of switching can be found. So, winner’s sum (the m-th participant) is defined as

M K 2 2 J             2 J             \

Nm

= E ЕП nrk 2 mM , n =1 , k 2 ,m,n Г =0            \r =0              /

n=m where K2 is common quality of realization оf pair evolution, which consists of J stages.

Conclusion

Concurrent game was represented as a relay-race, in which participants pass the distance, divided into stages, time of passing of which is known accurate to densities. Usage of the conception of M -parallel semi-Markov process allows to work out a recurrent procedure of relay-race evolution. On the base of common recursive procedure a pair evolution was constructed. For the pair evolution a mathematical expression for evaluation of winner’s sum is obtained. Expression for calculation of winner’s sum is the key to form the optimal strategies of multistage dynamical competitions in the case, when one can control the densities of passing by participants.

Further investigation in this area should be directed to find both formula, which connects quantities of participants and stages with total quantity of trajectories and formula, which permit to generate trajectories of relay-races evolution (now such trajectories are generated algorithmically), that helps to overcome curse of dimensionality. Also a mathematical apparatus, which connects the proposed models with classical game theory [14,15], and permits to build up optimal strategies of relay-race evolution, may be worked out.

Acknowledgements. The reported study was partially supported by RFBR and Tula Region Government, research project No. 16-41-710160 r_a.