Сингулярно возмущенная система параболических уравнений в критическом случае

1. Постановка задачи и регуляризация

Рассмотрим первую краевую задачу для систем сингулярно возмущенных параболических уравнений

L _s u ( x , t , s ) = s d _tu - 8 ² a ( x) d 2 u -

• — A    ( t ) u = f ( x , t ), ( x , t ) eQ ,

• ^u    | t = o = °, и | x = o = u | x = i = 0                (1)

где 8 >  0     -    малый    параметр,

Q = {( x , t ): x e (0,1), t e (0, T ]}. Задача (1) изучается при следующих предположениях:

• 1.    0 <  a ( x ) e C " [0,1],

  © Омуралиев А. С., Кулманбетова С., 2016

• 2.    m x m матрица A ( t ) имеет m простых собственных значений { λ_i ( t )} , удовлетворяющих условиям

^∗ Статья написана по материалам международного симпозиума "Дифференциальные уравнения. Сто лет математической науке Урала". Пермь. 16–19 мая 2016 .

A ( t ) e C “ ( [ 0, T ], C m 2 ) , f e C " ( q , C m )i .

• а)    A i (t ) ^ 0 ( i = 1,2,..., k );

• b)    ReV t ) < 0 ( i = k + 1, . , m );

• c)    Л '( t ) * ^ j ( t ) , ^v i * J , i , J = k + 1, m .

• 3.    A i (t ) = 0 ( i = 1,2, . , k ) соответствует k линейно независимых собственных векторов { b j ( t )}, i = 1, k .

Далее будет построена регуляризованная асимптотика [1] решения поставленной задачи. Отметим, что аналогичная задача изучена в [2], однако там получена асимптотика типа пограничного слоя.

Следуя [1], произведем регуляризацию задачи (1), для чего введем регуляризующие переменные [1], [3]:

t 1 t            ψ ( t )

т = -y, m-=-LA(s)ds = —— ε2      ε 0           ε i = k +1,...,m,

^T 0   ^д т ^-

T2= dt -

ϕ_l ( x )

^£ l = —j=~ , ⁿ l = ε

ϕ_l ( x )

,

A n , T 1 = Л ( t) d m - A ( t ),

^A £ , ^L £ = a ^{( x} ) £ ^Ll , £ , l = 1

P l ( X ) = ^{( - 1)} l ¹ J x

ε ³

ds

, l = 1,2,      (2)

и расширенную функцию

u ( M , £ ), M = ( x , t , П, £,т, M ), £ = (Й, £ 2 ), П = (П 1 , n 2 ), M = ⁽ M k + 1 , M k + 2 , - , M m )

такую, что u(M,£ )0=y( x, t ,£)= u(x, t,£),              (3)

0 = (п,£,т, m ),

^L n = a ^{( x} ) £ ^Ll , n , l = 1

^Ll , z = ²⁽P l ^{( x ) d} 2, z ⁺ P l ( ^{x ) d} z •

Введем классы функций, в которых будут решаться итерационные задачи:

m

U1 = {V1 (x, t): V1 (x, t) = £ v- (x, t) b- (t), i=1

v- ( x , t ) e C ' ( Q )},

Y( x , t , £ ) =

ϕ ( x ) ϕ ( x ) t ψ_i ( t )

I £ ’ ³ , £ 2 , £

U 2 = { ^ 2 ( N 1 ): V 2 ( N 2 ) = £ Y ( N 1 ) b i (t ), i = 1

Тогда, на основании (1), (2), (3), относительно расширенной функции получим

I ^Yi ^{( N} 1)| <  c ^exP

—

задачу

L_£u(M , £ ) = ¹ T 0 й + T 1 й - JL l uU + T ₂ й - ε^η

к

+ n 2 },

n

8т J

,

mm

-£-\[^ £ й - £ ² L_xu = f ( x , t ),

U 3 = { V 3 ( N 2 ): V 3 ( N 2 ) = £ £ [ C i,j ( x , t ) + i = 1 j = k + 1

u 1 1 = t = m = 0 0, u | x = 0, £ 1 = n 1 = 0 0, й\_х = 1 £ 2 = n ₂ = 0 = 0.                  (4)

Расширенная задача (4) регулярна по ε при £ ^ 0, ибо справедливо тождество

LuM , ^£ ) 0 = y ( x , t , £ ) = ^L £ ^{U ( x} , t , ^£ )•

1          £ \

+ £ ® l , j ( x , t )erfc I у | ]exp( m j ) b - ( t ),

l=1               к 2^ tJ ci, j(x, t), ®i, j-(x, t)e C w (Q)},

N 1 = ( x , t , п,т ), N 1 = ( x , t , £ , m ),

П = ⁽ П 1 , П 2 ), ^£ = ^{( £} 1 , ^£ 2 ^).

Из этих классов построим новый класс, как прямую сумму u = ®k=1 Uk, тогда произвольный элемент uv (M) e U этого класса запишется uv (M) = £m {Vv, i (x, t) + Yv, i (N1) + i=1

a m . k + 1 [— x . t ) +

+ £ 2 = 1 ^ j ^{( x} , t ^)erfc I ^£ | ^exp⁽ m j ^)} b ⁽ t ) • (6)

Уравнения (5) при v = - 2, - 1 однородные, поэтому они разрешимы в классе функций U и их решения представимы в виде (6), если функция Y_{v , i} ( N ₁) является решением уравнения

T v , i ( N 1 ) = A n Y v , i ( N 1 ), v = - 2, - 1 (7) c краевыми условиями

Y v , i ( N i)\_t = t = o = 0,

Y v , i (МЖ= 0 = d V, i ( x , t ),

Y v , i ( N 1 )\ n 2 = 0 = d vi ( x , t ),                 (8)

^dv , i ^{( l} - 1, t ) = ^-V v , i ^{( l} - 1, t ) ,

V = - 2, - 1.

ηk           ηkdv zk      I----- , dZk      I-------Г ’

^{2 dT - v}         4^(т - v ) ³

^{4( т - v} ) nV функцию (9) перепишем:

Решение этой задачи имеет вид [4, c. 196]

Y v , i ( N) =

² d^l ( x , t )

Y . 2 N 1 ) = S     ’

l = 1

4 π

Г ^            2

j n^ ^4exp^{( -} zk ) ^x

2 τ

= x d v , i ⁽ x , t ) f₀ ^T j^ Z 1 G ( n , ^Z , ^{T -}

z ) I Z i = 0 d ^z 3 - l^dz =

г' 2 z_{k r} x   ——[exp

^J 0 nk ^P

c

—

⁽ n ^{- Z}l ^{) 2} 2 z_k

\

x [exp

x< exp

к

= X d v , i ( X , t ) I l (n ),             (9)

l = 1

^{G (} П 1 ,П 2 , ^Z 1 , ^Z 2 , t ) = 1- ^x

4 πt

^{( n} 1 ^{- Z} 1 ^{) 2}

exp

I

I

exp

—

^{( n} l ^{+ Z} l ^{) 2}

к     4 n 2

^{( n} 2 ^{- Z} 2 ) 2

( exp

I

^{( n} 2 ^{+ Z} 2 )

При т = t = 0 полученное решение обращается в нуль, поэтому значение функций l                     :l dv, i(x, t )\ t =0 = dv, i( x)            (10)

принимаем произвольно и это допущение будет использовано ниже.

Теорема 1. Для решения задачи (7), (8)

справедлива оценка

Y v , i ( N 1 )

< c exp

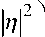
8т к 2

| n = J П 1 + П 2 .

Доказательство. Заметив, что

d

— ( G ( n , £ , т - v )) ^ = 0 =

---------x 4п(т - v )

(     „2 I

^{П к} exp—

( т - v )     к 4( т - v ) J

x

x <  exp

(m-ii?

4( т - v ) J

( exp

к

n i i f |

4( т - v ) J

k ^ l , k , l = 1,2,

и, произведя замену:

4 η_k ²

—

^zk ] d ^Z l^dzk .

Таким образом, замена

^{( n l} ± ^{Z l} ) ^z k = t_l , dt_l =± z^dZi η_k            η_k

во внутреннем интеграле приведет к виду

^2, d v i ( X , t ) р^             л

Yv,i(N1) = S   }----1 nk 4 exp(-z2 ) x l=1  4п  2 т

ηlzk xf0 nk exp(-12)dtl.

Отсюда, используя неравенство [6, с. 352] и формулу 3.323 из [7], получим требуемую оценку.

Теорема доказана.

Вычислим свободный член итерационного уравнения (5) при k = 0

F 0 ( M ) = - 7 1 u - 2 ( M ) =

= - S Л ( t ) [ v - 2,i (X , t ) + Y - 2, i ( N 1 ) ] b i (t ) - i = k + 1

- S ( ^ j ( t ) - Л ( t ) ) x i , j = k + 1

^x c i -,² ( x , t ) ⁺ s ^ ij¹ ( x , t ^)erfc ⁽ 2^ l^

^{x e}xp⁽ и ) b i⁽ t ) ^-

- S S ^ ( t ) [ c - j ( x , t ) + i = 1 j = k + 1

+ S ®Уl (x, t )erfc l=1

( ■ I к 2 -Л 2,

^{x e}xp⁽ ^ j ) ^b i⁽ t ).

x

x

Обеспечивая разрешимость в U уравнения с такой правой частью, положим c ^- ( x , t ) = 0, o ^- , l ( x, t ) = 0,

V i ^ j &1, m , j = k + 1, m , v - 2 i = 0 V i = k + 1, m , а функции v - 2, i ( x , t ) V i = 1, k , c^{- 2} ( x , t ), -2. 1/

Юц , (x , t ) V i = k + 1, m являются произвольными. При таком выборе функций свободный член примет вид

m

F o ( m ) = - £ Л ( t ) Y - 2,i ( N 1 b i ( t ).

i = k + 1

Решением краевой задачи (5) при k = 0 со свободным членом F ₀( M ) будет функция (6) при v = 0, если Y o, _i ( N i ) будет решением неоднородного уравнения (7) с правой частью F ₀( M ) и краевыми условиями вида (8). Решением этой задачи будет (см. [4, с. 196])

T рЮ рю

^Y „( ^N 1 ) = - Л ( t ) J o J o J o ^Y - 2, , ( ^N 1 ) x ^x G П 1 ,п 2 , Z 1 , Z 2 , T - z ) dZ 1 dZ 2 dz +

+£ d 0,i( x, t) x l=1

T рю

^X j ₀ j ₀ ^d Z l ^{( G} (П 1 Л 2 , ^Z 1 , ^Z 2 ^{, T}

- z ) dZ _{3 -} l dz .

Теорема 2. Пусть

I Y - 2, i ^{( N} 1)| <  c exP

тогда справедлива оценка

I ^Y 0, i ^{( N} 1)1 <  ^c exP

И11

8 τ

η

8 t

Доказательство проводится аналогично и на основе предыдущей теоремы 1.

В следующее итерационное уравнение войдет член L _n u _{- 2}( M ), присутствие которого

или выбирая

2^l'( x )5 xd- 2 i (x, t) + $( x) d- 2 i (x, t) = 0 (12) обеспечим требуемое соотношение. Ниже будет показано, что функция d- 2 i (x, t) имеет вид d-2,i(x, t) = d-2,i(x)P(t) + P2(t).     (13)

j = k +1, m , v-1i = 0 V i = k +1, m , а функции v-1, i (x, t) V i = 1, k, c- 1( x, t), of11 (x, t) V i = k +1, m являются произвольными функциями. Тогда решение этого уравнения представимо в виде (6) с индексом v = 1, если Y1i (N1) - решение неоднородного уравнения вида (7). Функция Y1,i(N1) , как решение неоднородного уравнения вида (7) представимо в виде, аналогичном (11).

Следующее итерационное уравнение после соответствующих действий, приводящих к соотношению L _n u - 1 ( M ) = 0, имеет свободный член и представимо в виде

F 2 (M ) = - Tu о - T 2 u - 2 + f ( x , t ) = mm

=£fi(x)b(t)- £ (л(t)-A(t))x i =1                         i, j = k +1

^c 0 j ^{( x} , t ) ⁺ £ o t'^{( x} , t ^)erfc ^ ^

X

выведет решение из класса U . Обеспечивая разрешимость этого уравнения в данном классе, обратим этот член в нуль. Для чего вычислим

km x exp(^.)bi(t) -£ £ л(t)x i=1 j=k +1

x

^c 0 j ^{( x} , t ) ⁺ £ o t'^{( x} , t ^)erfc ^ 2 2t

x

L n U - 2 ( M ) =

= a(x)£ £[2^/(x)dxd-2,i (x, t) + i=1 l=1

+ ^ ; ⁽ x ) d - 2, i ⁽ x , t ^{)] d} n l l ⁽ n ^{, T} ) b i⁽ t ) = ⁰

m x exp(Vj)bi(t)- £ л(t)[v0,i(x, t) + j=k +1

k

-Yo/N1)] b.( t)-£[d tv -2,i( x, t) + i=1

+ E а^( t ) v - J x , t )Ь( t ) - j = 1

• - E v - 2, i ( x , t ) £ ^a j A t ) b ( t ) ^- i = 1                 j = k + 1

• - £ to t d - 2, ( x , t ) + i = 1 I = 1

• ⁺ E ^a i,j ( t) ^d l - 2, j ( x , t ) b i ( t ) I(ПТ ) ^-

• J=1

• ^-    £ ^{[ d} с - 2 ( x , t ) ⁺ a , i ( t ) cl 2 ( x , t ^{)] x} i = k + 1

^x exp( U )hlt ) ^-

• ^- E £ a j ( t)c - 2 ( ^x , t) ^b j ⁽ t ^)exp⁽ ^) ^- i = k + 1 j = 1( i ^ j )

m 2

• -EE^ a(x, t)+

i = k + 1 l = 1

+ a ( t)a - 2,^l ( x , t )]erfc |       | x

• i , i       i , i                  <  27 1 J

x exp( и ) bi( t)- mm2

• ^- E E E ^a i, j ⁽ t ^{) a -}2’‘ ^{( x} , t ^)erfc I      I^х

i=k+1 j=1(i^j) i=1                              \ 2v t j xbi( t )exp( ^J), fl(x) = (f(x, t),b*(t)).

Обеспечивая разрешимость итерационного уравнения (5) при k = 2, произведем следующие приравнивания: k d tv-2, i(x, t)+E a j (t) v-2, i(x, t)=f(x), i=1,k,

J = 1

k

A ⁽ t ) v 0. i ⁽ x , t ) = ^- E ^a i,J ⁽ t ) v - 2, J ⁽ x , t ) ^{+ f (} x ) ,

J = 1

i = k +1, m, dtd- 2,i( x, t) + E a,j (t) d- 2,J (x, t) = 0 V i = 1m, j=1

^d t ^c - ^{2 (} x , t ) ⁺ a , i ⁽ t ) ^c - ^{2 (} x , t ) = ⁰,

5 _taT 2, l ( x , t ) + a i i ( t ) a f 2, l ( x , t ) = 0 V i = k + 1, m , ( ^A j ⁽ t ) ^{- A} i ⁽ t ) ) ^{c 0} j ^{( x} , t ) = ^{- a} i , j ⁽ t ) c - j ^{( x} , t ),

( ^A j ⁽ t ) ^{- A} i ⁽ t ) ) rfj' ^{( x} , t ) = ^{- a} i , j ⁽ t ^{) d} j , J ^{( x} , t )

V i , J = k + 1, m ,

^A i ⁽ t ) c ⁰ j ⁽ x , t ) = - a j ⁽ t ) c ^{- (} x , t ),

A i ( t ^d j¹ ( x , t ) = - a i , j ( t ) a - J ( x , t )

V i = 1, k , J = k + 1, m .          (14)

Отметим, что решая уравнение (14) относительно   dl_ 2i (x, t)   при начальном условии (10), получим решение в виде (13). Найденное решение подставим в (12) и получим уравнение относительно d-2 i (x). Начальные условия для дифференциальных уравнений, вошедших в (14), определим из краевых условий для u -2( M), входящих в (5):

v-2,i( x ,0) = 0, Y-2/ N1)| T=0 = 0, ci-2(x,0) = -v-2,i (x,0), a-2,1 (x ,0) = a-2,l (x),

• V- 2, ( x , t )|     = - c -2( l - 1, t ),

xl 1

• Y -2, i ( N 1 )| _n = ₀ = d - 2, i ( x , t ),

d - 2, i ( x , t )| _; =- v - 2, i ( l - 1, t ), xl 1

l = 1,2, i = 1, m .

Отметим, что функция a - ², ^l ( x ), как и функция d - _{2 i} ( x ), аналогичным образом обеспечит выполнение соотношения L ^ u _{- 2} ( M ) = 0.

Свободный член F ₂( M ) , при таком выборе примет вид, подобный F ₀ ( M ) . Поэтому уравнение (5) при k = 2 разрешимо в U .

Далее, повторяя вышеописанный процесс, определим все коэффициенты частичной суммы:

n ^k

• u . п ( M ) = E £ ² U ( ^M ). k =- 2

• 4. Оценка остаточного члена

Таким образом, используя принцип максимума [5], подобно [3], легко устанавливается, что сужение этой суммы посредством регуляризующих функций является формальным асимптотическим решением исходной задачи (1), т.е. доказана

Теорема 3. Пусть выполнены условия 1)-4). Тогда сужение частичной суммы при в = y ( x , t , £ ) , полученного вышеописанным методом, является асимптотическим решением задачи (1), т.е. при достаточно малых £ и n = - 2, - 1,0,1,... справедлива оценка

||u ( x , t , £ ) - u_{e n} ( x , t , / ( x , t , £ ))|| <  £ .