Синтез и анализ зацепления червячной передачи самоблокирующегося дифференциала в обобщающих параметрах

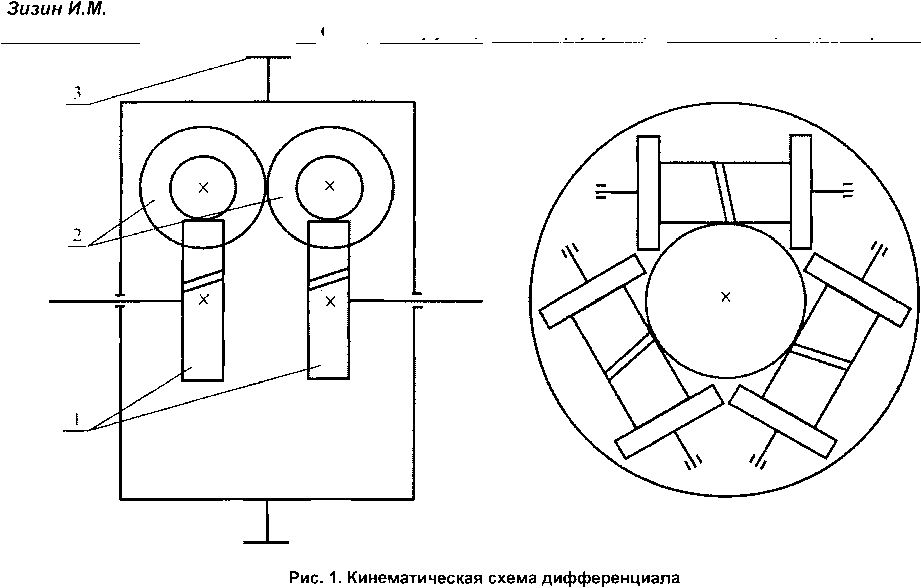
По заданию Уральского автомобильного завода на кафедре технической механики филиала ЮУрГУ в г. Златоусте разработана конструкция самоблокирующегося дифференциала автомобиля «Урал», обладающего соответствующими противобуксовочными качествами транспортного средства при движении по труднопроходимой местности. Дифференциальный эффект происходит при повороте автомобиля, когда полуоси вращаются с различными числами оборотов, вызывая при этом вращение полуосевых шестерен 1 и сателлитов 2, которое сопровождается возникновением сил трения в дифференциале. Самоблокировка обеспечивается за счет низкого КПД дифференциала при прямолинейном движении, а также в случае, когда сцепление с грунтом одного из ведущих колес понижено, то есть в случае, когда отсутствует относительное перемещение деталей дифференциала и они вращаются от приводного колеса 3 как одно целое с корпусом (рис. 1).

Согласно техническому заданию коэффициент блокировки К проектируемого дифференциала должен составлять порядка 1,9...3.

Коэффициент блокировки К есть величина, обратная коэффициенту полезного действия червячной передачи дифференциала ц, и определяется по формуле к = 1/17 = tg(X + p)/tg(X-p),                                                       (1)

где р = arctg (f) - угол трения; f- коэффициент трения скольжения; X- угол подъема витков червяка на делительном цилиндре.

По заданному значению К = 1,972 была рассчитана требуемая величина угла X = 23° 16' 11".

Задачей являлось создание дифференциала в определенных габаритах для помещения его в картер существующей серийной модели автомобиля. Межосевой угол в зацеплении равен 90°. Дифференциал включает в себя 6 червячных передач (рис. 2).

Синтез и анализ зацепления червячной передачи самоблокирующегося дифференциала в обобщающих параметрах

Особенности конструкции дифференциала приводят к тому, что витки червяка требуется выполнить на участке вала, ограниченном с обеих сторон поверхностями большего, чем диаметр червяка, размера. Поэтому при изготовлении червяка возникают существенные технологические трудности: ни один из обычно используемых для нарезания червяков способов не является приемлемым, так как требуемый способ должен обеспечить получение многозаходных червяков на «закрытых» участках вала. Поэтому для нарезания червяка был предложен метод зуботочения витков червяка с помощью эвольвентного зуборезного долбяка. При этом червяк, полученный в таком станочном зацеплении, является неэвольвентным. Указанный метод может быть реализован на серийном вертикальном зубофрезерном станке.

Если червяк нарезается косозубым долбяком и сцепляется с косозубым цилиндрическим эвольвентным колесом, являющимся копией долбяка, то по 2-му способу Оливье в полученной передаче будет реализован линейный контакт. Локализацию контакта можно осуществить следующим образом: нарезанный косозубым долбяком червяк зацепляется с косозубым цилиндрическим эвольвентным колесом, имеющим число зубьев меньше, чем у долбяка.

Таким образом, объектом данного исследования является червячная передача дифференциала с червяком, нарезаемым долбяком на зубофрезерном станке, и колесом, нарезанным червячной фрезой. Основной целью работы было исследование всех геометро-кинематических возможностей зацепления таких передач. Для этого была использована методология геометрического синтеза и анализа неэвольвентных пространственных зубчатых зацеплений в обобщающих координатах, разработанная профессором, доктором технических наук О.Н. Цукановым [1].

Расчет и конструирование

Согласно указанной методологии уравнения эвольвентной винтовой поверхности зубцов исходного звена представляются в виде функций обобщающих координат поверхности зацепления: торцового угла зацепления с^ и угла профиля эвольвентного зубца исходного звена ц, (рис. 3):

х = rb cos c^v + lb sin о^;

у = rb sin o^ - lb cos o^ (2) где rb - радиус основной окружности; lb - линейный параметр, определяющий положение точки эвольвентного профиля зубца на нормали к нему [1].

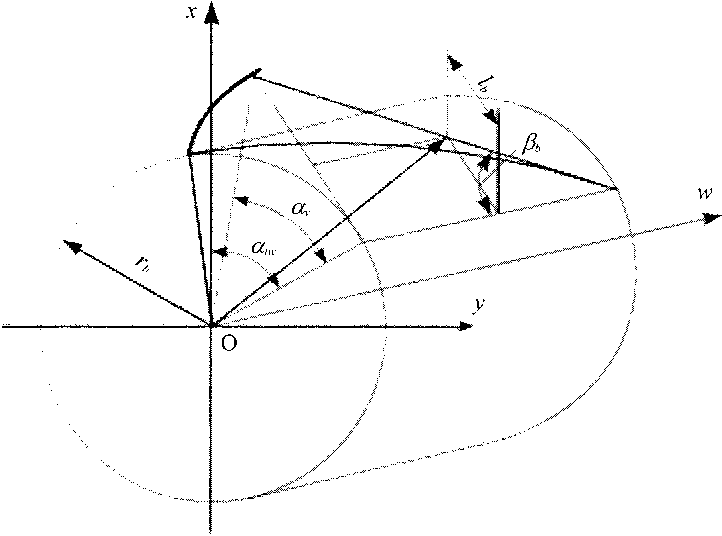
Рис. 3. Эвольвентная поверхность зубцов исходного звена в обобщающих параметрах

Радиус Гь является обобщающим параметром, определяющим масштаб передачи. Линейный параметр 1Ь является функцией обобщающих параметров гь , осу, угла наклона линии зубца на основном цилиндре рь, аппликаты w торцового сечения исходного звена:

1Ь ~ rb tg о^ -wtg/3b.(3)

Уравнения поверхности зубцов огибающего звена червяка, их подрезания и заострения получены с помощью формул преобразования систем координат из общих зависимостей, приведенных в [1].

Уравнения поверхности имеют вид:*

хч = х cos ф, + w sin фч — rw (1 — I/i) cos фч;

Уч = - х sin фч + w cos фч + rw (1 - I/i) sin фч;(4)

w4 = - у;

где фч - угол поворота червяка; r_w - радиус начальной окружности исходного звена; i = w_K/^₄ -передаточное отношение передачи; I = cos /3_WK /cos 3^ З^к, 3w4 - углы наклона линии зубьев колеса и червяка на их начальных поверхностях соответственно.

Уравнение зацепления, получаемое из основной теоремы зацепления, приводится к виду w = rb {tg /3btg Оу + [- cos o^tg Зь + tg 3b (1 - I/i) sec c^w0 -

• -    1 /i] / (- sin a^)} cos² Зь.                                                                            (5)

Исследование геометро-кинематических показателей (ГКП) зацепления выполняется в обобщенной (предельной) области его существования, ограниченной линиями подрезания и заострения зубцов огибающего звена.

Для определения координат точек кривых подрезания при задаваемых значениях торцового угла зацепления а^ угол а^ находится из уравнения tg ty = Datg Зь + lb* sec Зь.                                                                        (6)

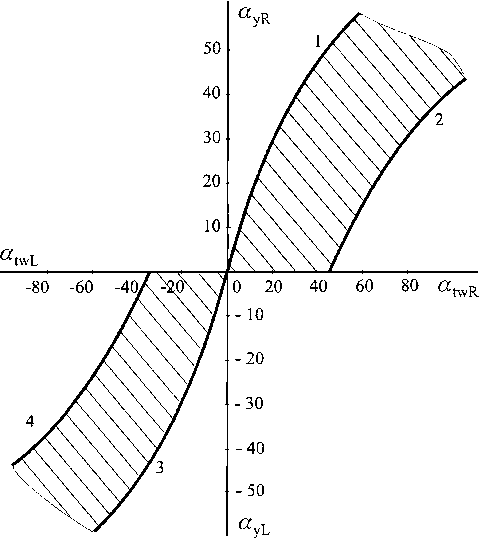
Рис. 4. Обобщенная область существования зацепления: 1,3- кривые подрезания; 2, 4 - кривые заострения

Зизин И.М.                                    Синтез и анализ зацепления червячной передачи самоблокирующегося дифференциала в обобщающих параметрах

Параметр 1Ь* определяется из квадратного уравнения

(-sin oQ l_b*² + {[(- tg p_b cos atw - Ei) (tg P_b + E_a) + EVi] cos p_b +

+ [(1 - Ei) sec O4_w0 - cos o^] sec ft} l_b* - cos o^Da^g p_b + E_a) = 0,                           (7)

где

D_a = [ - tg 3_b cos o^ + tg P_b (1 - Ei) sec о^₀ - l/i](- sin aQ;

E_a = {[(1 - Ei) tg P_b sec o^₀) - 1/i] cos a^ - tg ft} / sin² a%_w.

Для определения координат точек кривых заострения используется условие

Уь = Ук,                                                                                     (8)

вытекающее из равенства wkL = w^ = - у.

Задавая c^_R и c^_L = - c^_R, варьируем q^r в предполагаемом диапазоне. Из уравнения (8) находим о^_ь. Расчет производится до получения значений меньше некоторых наперед заданных величин Ах_ч, Ау_ч. По полученным значениям Qt_w? (Ху строятся кривые заострения.

По расчетным значениям обобщающих координат строится обобщенная область существования зацепления (ООСЗ), ограниченная формой и положением кривых подрезания и заострения (рис. 4).

Далее в этой области отыскиваются геометро-кинематические показатели зацепления, наиболее полно удовлетворяющие требованиям технического задания, и соответствующие значения параметров исходного контура.

В настоящее время получены благоприятные ГКП зацепления (при m = 4 мм, числах зубьев Zi = 21, z2 = 4) для случая использования стандартного исходного контура по ГОСТ 13755-81:

• -    коэффициент перекрытия - 2,67;

• -    главные приведенные кривизны в полюсе зацепления - 0,025 и 0,042 мм"¹;

• -    скорости скольжения в крайних точках зацепления -11 и 31 мм/с.

• 7. Лопатин, Б.А. Цилиндро-конические зубчатые передачи: монография / Б.А. Лопатин, О.Н. Цуканов. - Челябинск: Изд-во ЮУрГУ, 2005. - 200 с.

Дальнейшее исследование направлено на получение более благоприятных показателей без привязки к исходному контуру и данных о напряженно-деформированном состоянии зубьев, оценка которого выполняется в CAD-системе методом конечных элементов.