Синтез траекторий сборочно-сварочных роботов-манипуляторов в рабочей среде с препятствиями

В известных работах предложен ряд алгоритмов синтеза траекторий роботов в среде с препятствиями, которые основаны на дискретной модели свободного от столкновений конфигурационного пространства. Задача синтеза при этом сводится к поиску кратчайшего пути на графе, ребрам которого ставятся в соответствие линейные либо дуговые фрагменты траектории робота, при движении по которым отсутствуют столкновения и удовлетворяются конструктивные ограничения [1; 2]. В ряде последних исследований реализованы алгоритмы синтеза, выполняющие поиск нескольких решений, что увеличивает вероятность нахождения траектории за фиксированное время [3–4]. В частности, в работе [5] синтез реализован с использованием концепции мультиграфа задачи движения (TMM).

Необходимо отметить, что известные алгоритмы синтеза траекторий позволяют эффективно обойти проблему размерности конфигурационного пространства роботов [6–9], но не учитывают форму препятствий и форму звеньев манипулятора, что приводит к реализации траекторий низкого качества с большим объемом движений [6]. При использовании таких алгоритмов траектория робота может быть найдена за конечное время также лишь с определенной вероятностью, т.е. свойство «полноты» решения теряется [6; 10].

В данной работе предложен новый комбинированный метод синтеза траекторий роботов-манипуляторов в рабочей среде с препятствиями, основанный на использовании решетчатой дискретизации «насыщенных» препятствиями зон конфигурационного пространства. Такой подход в отличие от известных позволяет эффективно учесть сложную форму препятствий, характерную для сборочно-сварочных роботизированных комплексов. В соответствии с этим подходом синтез свободной от столкновений траектории осуществляется путем поиска кратчайшего пути на графе, ребрам которого ставятся в соответствие линейные движения робота между промежуточными конфигурациями, найденными как путем рандомизированной дискретизации (в зонах с малым количеством препятствий), так и путем решетчатой дискретизации (в зонах с большим количеством препятствий сложной формы.) Такой метод позволяет синтезировать участки траекторий робота в наиболее сложных зонах выполнения технологических операций сборки/ сварки без предварительной проверки его движений на столкновение, что обеспечивает приемлемое для практики количество тестов столкновения при сохранении свойства «полноты» при фиксированном шаге дискретизации.

Комбинированный метод синтеза траектории роботов-манипуляторов

Рассмотрим робот-манипулятор, имеющий n поворотных сочленений, в рабочей зоне которого расположено некоторое мно- жество препятствий B = {B 1, B2, ..., Bm}. Конфигурацию этого робота зададим в виде вектора q = [qi]T, где qi – величины углов в сочленениях (i = 1:n). Ограничения на изменения углов в сочленениях зададим в виде qmin < q < qmax, где qmin, qmax - векторы, определяющие нижнее и верхнее конструктивные ограничения на изменение углов в сочленениях робота-манипулятора. Зададим геометрическую модель робота-манипулятора, установленного в конфигурацию q, в виде множества М(q). Тогда свободное от столкновений конфигурационное пространство определяется как

C f = { q е C | M ( q ) _n B = 0 }. (1)

Задача определения пересечения множеств М(q) и B решается путем проведения теста столкновения между роботом и препятствиями [2]. Прямолинейный участок траектории между двумя конфигурациями qa и qb (a # b, qa, qb е Cf,) задается в виде множества векторов dab = {dk I M(dk) n B = 0}. (2) где dk = qa+(h I Nh)(qb - qa), h = 0: Nh, Nh > N - параметр дискретизации прямолинейного участка траектории.

Дискретная конфигурация робота q _b е C f является соседней с конфигурацией q _a е C_f , если между ними существует прямолинейный участок траектории d ab и D ( q a , q _b ) <  d , где D (•) - симметричная функция, характеризующая расстояние между двумя локациями робота-манипулятора. Траектория, соединяющая стартовую q s 1 и целевую q sg конфигурации робота, представляет собой последовательность, состоящую из соседних конфигураций q s 1 , q s ₂, „., q sg е DC f , и прямолинейных участков, соединяющих эти конфигурации, d s 1 s ₂, d s 1 s ₂, •", d ( sg -1) sg . В качестве критерия качества траектории движения робота манипулятора при сварке шва предлагается использовать суммарное время перемещения технологического инструмента:

τ = N Δ t + ρ/ν, (3) где N – количество операций, выполняемых роботом в технологическом процессе сбор-ки/сварки; ∆ t – время выполнения одной операции; ρ – длина пути технологического инструмента при его движении в направлении от начальной к конечной локации;

ИССЛЕДОВАНИЯ v - скорость движения технологического инструмента.

Тогда задача синтеза траектории робота-манипулятора может быть сформулирована следующим образом: среди всех последовательностей дискретных конфигураций q s i , q s 2 , • ••, q _sg ^G C f , координаты которых лежат внутри области, ограниченной предельно допустимыми значениями углов в сочленениях q min <  q <  q max , найти последовательность , на которой критерий качества (3) ³⁸ достигает минимума.

Для описания конфигурационного пространства робота примененная статистическая модель представляется в виде неориентированного графа R = ( V, E ). Вершины V этого графа являют собой множество свободных от столкновений конфигураций робота, координаты которых – случайные величины.

Формирование множества V осуществляется следующим образом: генерируется случайная конфигурация робота-манипулятора и выполняется тест столкновения робота с препятствиями. Если столкновения нет, то конфигурация добавляется в множество V , в противном случае она отбрасывается. Ребрам Е графа ставятся в соответствие прямолинейные участки траекторий между свободными от столкновений конфигурациями (рис. 1, а ). Зона, насыщенная препятствиями, так называемый «узкий коридор» (рис. 1, б ), дискретизируется регулярной решеткой, поскольку вероятность выявления такой зоны рандомизированным методом близка к нулю [1]. Соответствующие вершины и ребра решетки добавляются в граф R . Такой подход к формированию статистической модели позволяет эффективно решить проблему раз-

мерности, возникающую при планировании траекторий промышленных роботов-манипуляторов [1; 2; 6].

Предложенный комбинированный метод синтеза траектории предполагает реализацию следующих этапов:

• 1.    Генерируется множество V , состоящее из N max свободных от столкновений конфигураций робота-манипулятора.

• 2.    Выполняется поиск прямолинейных участков траекторий между соседними конфигурациями q i , q j , и найденные участки заносятся в множество E .

• 3.    Если между соседними конфигурациями q _i , q _j нет прямолинейного участка траектории и эти конфигурации находятся в зоне, насыщенной препятствиями, то выполняется поиск криволинейного участка траектории между q _i и q _j , дискретизированного регулярной решеткой G . Если такой участок траектории найден, то он добавляется в граф R .

• 4.    Формирование множества E выполняется путем циклического повторения шагов 2, 3 K _max раз.

• 5.    Выполняется поиск кратчайшего пути на графе R , исходя из критерия качества (3).

Алгоритм синтеза траектории роботов-манипуляторов

С учетом специфики и возможностей геометрического моделирования роботов-манипуляторов в современных CAD-системах на основе предложенного метода разработан алгоритм планирования траектории, ориентированный на интеграцию в систему автономного программирования сборочно-сварочных РТК (табл. 1). Алгоритм использует следующие обозначения. Randq – функция генерации

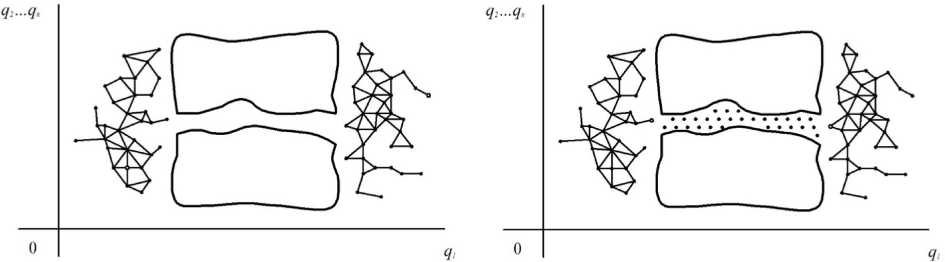
Рис. 1. Комбинированный подход к дискретизации конфигурационного пространства робота-манипулятора

вектора конфигурации с координатами, имеющими случайные значения в допустимом диапазоне q min <  q <  q max . Rand - функция генерации случайных целых чисел i ≠ j в диапазоне от 1 до N _max. EPath – функция вычисления прямолинейного участка траектории между двумя конфигурациями q i и q j . TTest - функция, выполняющая оценку «насыщенности» окрестности конфигурации q препятствиями путем генерации случайных конфигураций в ее окрестности и тестирования их на столкновение. В случае если количество столкновений превышает допустимый предел, функция TTest возвращает 1, указывая на то, что окрестность конфигурации q «насыщена» препятствиями. Connect - функция, выполняющая поиск конфигураций ( q i , q J ) на решетке дискретизации G , являющихся соседними с конфигурациями ( q i , q j ). GraphSearch - функция поиска кратчайшего пути на графе R , исходя из критерия качества (3).

Таблица 1

Алгоритм синтеза траектории сборочно-сварочных роботов манипуляторов

Исходные данные :

геометрическая модель РТК - М ( q ), B , начальная и целевая конфигурации робота - q s , q g .

• 1:    i — 1; V — q _s , q _g ;

• 2:    повторять

• 3:     q _i ← Randq ;

• 4:      если q i e Cf

• 5:         то V — q i ;

• 6:      i ← i +1;

• 7:    до тех пор пока i_max;

• 8:    k← 1

• 9:    повторять

• 10:    ( ij ')— Rand (1, N max );

• 11:     если ( D ( q i , q j )< d и EPath ( q i , q j )* 0

• 12:      то Е ^ EPath ( q i , q j )

• 13:     иначе

• 14:         если ( D ( q _i , q _j )< d и ( TTest ( q _i )=1 или TTest ( q _j )=1))

• ^15:              то ( q i , q g ) ^ Connect ( q , , q j , G ) ,

• ^16:               R ^ SearchGridPath ( q , , q J ) ,

• ^17:                V ^ ( EPath ( q , , q i ) , EPpath ( q , , q J ) );

• 18:     k←k+ 1;

• 19:    до тех пор пока k_max;

• 20:    path ^ GraphSearch ( R , q s , q g );

Особого внимания заслуживает рассмотрение процедуры SearchGridPath, разработанной на основе методики, предложенной в предыдущих работах авторов данной статьи [11–14]. Процедура выполняет поиск криволинейной траектории между двумя конфигурациями робота-манипулято ра (qi,qJ) путем дискретизации окрестности данных конфигураций дискретной решеткой. Соответственно, в результате выполнения процедуры в граф R добавляются вершины и ребра, принадлежавшие криволинейному участку траектории между (qi,qj) . Алгоритм процедуры SearchGridPath приведен в табл. 2.

Алгоритм использует следующие обозначения: N ₀ – начальное значение параметра дискретизации конфигурационного пространства робота решеткой; N _max – максимально допустимое значение параметра дискретизации конфигурационного пространства робота решеткой; N_s - шаг изменения параметра дискретизации; P – криволинейная траектория робота.

Алгоритм использует следующие функции: maxf( ф _b ) - функция, возвращающая максимальное значение весовой ф из множества ф _b ; maxb ( ф _bk ) - функция, возвращающая индекс b максимального значения весовой функции из множества ф _b ; q (ф) - функция, возвращающая конфигурацию робота, соответствующую значению весовой функции ϕ; explore ( q (ф a ), q (ф _b )) - функция проверки существования прямолинейного участка траек-

Таблица 2

Алгоритм процедуры SearchGridPath

Исходные данные:

геометрическая модель РТК – М(q), B, начальная и целевая конфигурации робота – qs 1 = qi, qSg = j_________________________

• 1:    Установить начальное значение параметра

дискретизации N←N ₀;

повторять

Вычислить V _a для параметра дискретизации N ;

Установить весовые коэффициенты для ребер решетки T ab ^ 1/3 n ( k=1:d );

повторять

Вычислить весовую функцию ф a ( a =1: Nⁿ );

a — s 1;

повторять ф—тахfфbk);

b —max b ( ф b );

p ^— explore ⁽ q ^{( ф} _а ), q ^{( ф} ь ));

P —{ q ( ф a ), q ( ф b )};

если b = sg , то возвратить фрагмент траектории P ; a — b ;

до тех пор пока p =0;

T ab k ← 0;

P —0;

до тех пор пока ф _s 1 =0;

N — N + N _s ;

до тех пор пока N < N max .

ИССЛЕДОВАНИЯ тории между двумя конфигурациями робота q(ϕa) и q(ϕb) в соответствии с формулой (2). Если такой участок траектории существует, функция возвращает «1», в противном случае она возвращает «0».

Данный алгоритм функционирует следующим образом. Первоначально конфигурационное пространство робота дискретизируется с низким разрешением N 0 ₉, и предполагается, что между всеми соседними конфигурациями существуют прямолиней- ⁴⁰ ные участки траектории, т.е. всем весовым коэффициентам ребер решетки присваивается значение 1/3 n . Далее вычисляется весовая функция для каждого узла решетки ф а ( a = 1 : N n ) и ищется траектория между стартовой q _s1 и целевой q sg конфигурациями путем подъема в направлении градиента весовой функции узлов решетки. Для этого отрезки, соединяющие соседние конфигурации q _a и q _b , дискретизируются с высоким разрешением N_h в соответствии с (2) и для каждой дискретной конфигурации робота d k выполняется тест столкновения. Если столкновения отсутствуют, то выбираются две новые конфигурации на решетке низкого разрешения в направлении градиента. Если обнаружено столкновение, то значение весового коэффициента ребра решетки T ab устанавливается в нуль.

Значения весовой функции f_a для каждого узла решетки вычисляются на основе следующей итерационной формулы:

( >

Ф ! ,' ^{+ 1 )} = f a, У T b, ^5 + V . ,           (4)

V к=1                / где l - номер итерации; Va - параметр, значение которого определяется следующим образом: Va = -1, если qa ё Cf, Va = 1, если qa = qSg, Va = 0 во всех остальных случаях.

Нелинейная функция f a имеет следующий вид:

• fa ( А ' ) =

,       0"

tanh ( а ) ,

если а <  0, если а >  0.

Величина весовых коэффициентов ребер решетки T _ab выбирается исходя из достаточных условий сходимости итерационной процедуры (4), полученных в работах [11; 14]. В частности, T _ab = 13 n , если существует прямолинейный участок траектории между конфигурациями q _a и q b_k и T ab = 0 в противном случае.