Систематизация преподавания математических дисциплин на факультетах агробиологических направлений

Основная задача вузов состоит в подготовке высококвалифицированных специалистов. Это требует дальнейшего совершенствования учебного процесса путем изменения, как методики преподавания дисциплин, так и их содержания. Высокая конкуренция на внутреннем и внешнем рынках требует обеспечить подготовку высокообразованных людей и высококвалифицированных специалистов, способных к профессиональному росту в условиях развития новых технологий. Прежде всего, важен общий интеллектуальный уровень, ибо отдельная личность при наличии особых способностей эффективно функционирует, как проводник идей, сформированных в массе. Поэтому образовательные системы должны не только систематизировать современные знания, но и учить, как систематизировать полученную информацию. Необходима систематизация учебного материала с целью повышения информативности предмета и развития более высокого уровня мышления учащихся.

Первый фактор - классификация разделов математики по уровню познания.

Второй фактор - представление математики как базовой для всех дисциплин. Дело в том, что ряд математических понятий при изучении других предметов изменяется. Преподавателям следует установить межпредметные связи, знать программы друг друга, выработать единый подход к изложению однотипных понятий, условиться о едином обозначении математических величин, используемых в различных предметах.

Третий фактор - аналогии и логическая связь отдельных разделов математики. Это формирует долговременную память и создает условия для более высокого уровня мышления. Аналогии же позволяют облегчить восприятие нового материала, помогают строить умозаключения, подобные уже имеющимся, но примененные к новым математическим объектам.

Четвертый фактор – общие методы решения математических задач при изучении других дисциплин. Обобщенные методы решения задач базируются на введении фундаментальных методологических понятий. Далее анализируются задачи курса, проводится классификация методов решения и разработка универсальных методов решения, что позволяет производить решения любой задачи с использованием обобщенной методики.

Пятый фактор – разработка заданий с межпредметным содержанием [1,2,3].

Шестой фактор – разработка заданий связанных с будущим местом работы.

Потребности работодателей и продиктовали необходимость создания программ прикладного бакалавриата. Очевидно, что прикладной бакалавриат будет популярнее обычного. В наше время получение высшего образования является почетной задачей практически каждого, а качество образования, к сожалению, интересует немногих. Студенты, окончившие традиционный бакалавриат получили общее высшее образование, и обычно работодатель их доучивает или сразу переучивать под конкретное рабочее место [2].

Математические методы все больше проникают во все сферы нашего общества, поэтому, необходим высокий уровень математической подготовки выпускников ВУЗа. Основной задачей изучения дисциплины «Математика» студентами агрономических специальностей является формирование базового комплекса основных теоретических и практических знаний по всем разделам математики с прикладной направленностью, а также развитие логического мышления, повышение интеллекта студентов, математической культуры [1-5].

От молодых специалистов ждут ответственности, способности логично мыслить, анализировать и прогнозировать результаты своей деятельности. И математика способствует формированию этих способностей [6].

На занятиях, в процессе изучения математики, у студентов формируется системность мышления и действий, умение абстрагировать мышление, способность к анализу. Однако, очень часто, студенты задают преподавателю вопрос: зачем им математика, как она пригодится в выбранной профессии? Ответить на эти вопросы, а также показать студентам связь математики с их будущей специальностью, кроме факторов, рассмотренных в статье «Факторы, систематизирующие изучение математики в вузе» позволяют задачи прикладного характера. Учащемуся необходимо видеть связь применения математических методов к решению задачи на конкретном примере. Рассмотрим задачу статистики. Для студентов направления подготовки 35.03.04 «Агрономия» [5].

На практике часто приходится иметь дело с зависимостью между переменными более сложной, чем функциональная - если каждому значению одной случайной величины поставлено в соответствие одно значение другой. Такова, например, зависимость между количеством посеянных семян X и собранным урожаем Y . Здесь каждому значению величины X соответствует множество возможных значений величины Y . Вместе с тем, как показывает опыт, оба признака могут быть подвержены воздействию случайных факторов, причем среди них могут быть и общие для обоих признаков. Поэтому средний урожай является функцией зависящей от количества семян. Такого рода зависимости относятся к корреляционным.

Пример. Были произведены измерения общей массы X десяти гроздей винограда сорта «Изабелла» в граммах и количества ягод в каждой грозди Y . Значения двух переменных представлены в следующей таблице:

Таблица - 1

Х	120	145	150	155	157	163	174	186	200	240
Y	38	43	50	52	57	58	65	62	70	80

Вычислить выборочный коэффициент корреляции, коэффициент регрессии Y по X и найти выборочное уравнение прямой регрессии Y на X .

Решение. Составим вспомогательную таблицу, в ней результаты измерений записаны во второй и третий столбцы. Внизу каждого из этих столбцов вычислены суммы для нахождения средних значений массы грозди винограда x и количества ягод y . Далее расположены столбцы, в которых вычисляются разности x. — xB и y. — yB, их квадраты и произведения. Затем значения этих столбцов суммируются. Надо отметить, что суммы в столбцах, в которых вычислены разности x — xB и y. — ув, будут всегда равны нулю.

Таблица - 2

	х i	y i	x — x B	( x — хв ) 2	У г — У в	( У i — У в ) 2	( x , — x B )( У г — У в )
1	120	28	-49	2401	-20	400	980
2	145	43	-24	576	-15	225	360
3	150	55	-19	361	-3	9	57
4	155	52	-14	196	-6	36	84
5	157	57	-12	144	-1	1	12
6	153	58	-6	36	0	0	0
7	174	65	5	25	7	49	35
8	186	62	17	289	4	16	68
9	200	70	31	961	12	144	372
10	240	80	71	5041	22	484	1562
Е	1690	580	0	10030	0	1364	3530

Находим средние значения x и y :

xB = -Е x = n

= 169. Ув = - Е у, = n

= 58.

Вычислим выборочный коэффициент корреляции, используя форму- лу:

г

B

Z(x- xBXy , — y.)

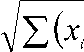
— xB )2 Jl( У,— Ув У

необходимые величины берем из вспомогательной таблицы:

Е⁽ x ^{— х}в Н у , ^— У в ) = ³⁵³⁰, 2 ( x ^{— х}в ^{) 2} = ¹⁰⁰³⁰, 2 ( у , ^{— у}в ^{) 2} = ¹³⁶⁴ •

Подставляя эти значения в формулу для вычисления коэффициента корреляции, получим

г

B

10030 • J13 64

« 0,95 •

Таким образом, коэффициента корреляции равен r_B ~ 0,95 , что говорит об очень сильной линейной зависимости между переменными Y и X . Найдем теперь выборочное уравнение прямой регрессии Y на X .

Это уравнение имеет вид: y — y_B = г_в —- ( x — x_B ) .

° х

За приближенные значения ах и (Гу - средние квадратические откло- нения параметров x и у соответственно, принимают соответственно значения, вычисленные по формулам:

°х ” аКx,—xJ. ^, * д—1тZ(у, — yB)2 •

V n — 1                     n — 1

Тогда

• 5-    = /^(У— IBS) = 1.1361 ~ 70,1359 » 0,36.

^X  тx-x.)2   V10030 v ,       ’

Подставляя, полученные значения, в выборочное уравнение прямой регрессии Y на X :

xB = 169, yB = 58, rs ~ 0,95, —L = 0,36, получим ^X

y - 58 = 0,95 ■ 0,36 •(x -169),

y - 58 = 0,34x - 57,46, y = 0,34x + 0,54 - искомое уравнение прямой регрессии Yна X.

Коэффициент прямой регрессии равен

Pyx = Г,    = 0,34

П

и показы-

вает, как в среднем изменится количество ягод в каждой грозди, если общая масса грозди винограда увеличится на один грамм. Представим данные измерения и полученные результаты графически :

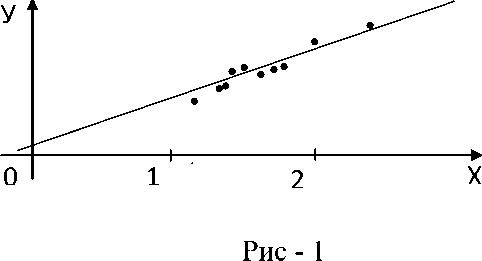
Прикладные задачи являются важным средством обучения математике. С их помощью студенты получают опыт работы с величинами, постигают взаимосвязи между ними, получают опыт применения математики в их дальнейшей профессиональной жизни.