Скалярно-тензорные теории гравитации, согласованные по наблюдательным ограничениям

В настоящее время рассматривается большое количество космологических моделей на основе различных типов материальных полей [1-3] и модификаций теории гравитации Эйнштейна [4-6]. Данные космологические модели можно рассматривать как развитие первых моделей, основанных на эволюции определенного скалярного поля и гравитации Эйнштейна (см. обзор в [7,8]). Причинами модификации исходных инфляционных моделей являются необходимость учета эффектов квантовой теории гравитации на ранней стадии эволюции Вселенной [9] и объяснения повторного ускоренного расширения Вселенной в современную эпоху [10,11].

Одной из первых модификаций ОТО являются скалярно-тензорные теории гравитации (СТГ) [12]. Этот тип модифицированных теорий гравитации успешно решает проблемы построения непротиворечивых сценариев эволюции ранней Вселенной и ее многократного ускоренного расширения. Следует также отметить, что скорость распространения гравитационных волн в случае скалярно-тензорных теорий гравитации равна скорости света в вакууме, как и в случае гравитации Эйнштейна [13,14], что соответствует недавним измерениям характеристик гравитационных волн от слияний черных дыр и нейтронных звезд [15].

Построение инфляционных сценариев на основе скалярно-тензорных теорий гравитации проводилось в различных исследованиях с использованием точных и приближенных решений уравнений космологической динамики [12,18,19]. В качестве важного критерия корректности моделей ранней Вселенной рассматривается соответствие спектральных параметров космологических возмущений наблюдательным ограничениям, полученным из измерений анизотропии и поляризации реликтового излучения [16,17].

Также отметим, что для случая скалярно-тензорных теорий гравитации основными параметрами, характеризующими тип космологической модели ранней Вселенной, являются: функция неминимальной связи F ( 0 ), которая определяет тип СТГ, и параметр Хаббла Н (。， соответствующий динамике ускоренного расширения Вселенной [12]. Поэтому, для построения и анализа космологических моделей можно определить соотношения между этими параметрами, подразумевающие возможность соответствия наблюдательным данным.

В настоящей работе рассматривается метод построения верифицированных по наблюдательным данным космологических моделей на основе данного подхода. Приводятся примеры космологических моделей на основе скалярно-тензорной гравитации, соответствующие наблюдательным данным. Также рассматривается обобщение данного метода на случай неминимальной связи скалярного поля и скаляра Гаусс а-Бонне. В заключении рассматриваются перспективы развития предложенного подхода к построению космологических моделей на основе скалярно-тензорной гравитации.

• 1.    Согласованные скалярно-тензорные теории гравитации

В представленной работе рассматриваются обобщенные скалярно-тензорные теории гравитации, действие которых можно привести к виду

S

5- / {ғ(0)А - ®(⁰⁾g“" 。屮。 ,"- 2V(⁰⁾}У-^"⁴т + s_m. 2K

⑴

Здесь к - эйнштейновская гравитационная постоянная¹, дН" - контравариаіітііые компоненты метрического тензора, R - скалярная кривизна, Ғ(0), ®(0), V(0) - некоторые дифференцируемые функции скалярного поля 0, S_m - интеграл действия материалыіых полей. Функция V(0) представляет собой потенциальную энергию или, как это принято в космологии, потенциал самодействия поля 0. При Ғ(0) = 1 модель с действием (1) переходит в эйнштейновскую теорию гравитации в присутствии неканонического скалярного поля с потенциалом самодействия.

Хотя при построении и анализе рассматриваемых моделей широко используются точные решения, вычисление параметров космологических неоднородностей проводится в приближении медленного скатывания [20]. Это связано с трудностью решения квантовомеханической задачи расчета генерации первичных неоднородностей из квантовых флуктуаций на стадии инфляции вне режима медленного скатывания. Метод расчёта параметров космологических возмущений в моделях скалярно-тензорной гравитации изначально рассматривался в работах [21,22]. В дальнейшем, данный метод использовался для оценки значений параметров космологических возмущений в работах [12,23-25].

Наборы данных, на согласование с которым проверяются космологические теории, разнообразны. Это данные по космическому микроволновому излучению, первичному нуклеосинтезу, первичным барионным осцилляциям, первичным чёрным дырам, локальным тестам в Солнечной системе и т.д. В данной работе проверяется соответствие ограничениям на специальные параметры космологических возмущений, которые получают прежде всего из наблюдений анизотропии реликтового излучения [16], [17]:

玉=0.9649 士 0.0042, (2) г < 0.035, ⑶ Ps = 2.1 X 10-9, ⑷ где ns — спектральный индекс скалярных неоднородностей, Ps — спектр скалярных возмущений, г — тензорно-скалярное отношение. Следует отметить, что верхняя оценка ⑶ на г указана для случая масштабно-инвариантного первичного спектра гравитационных волн.

Верификация моделей космологической инфяции по данным ограничениям является принципиальной, поскольку значения параметров космологических возмущений непосредственно связаны с фоновыми параметрами космологических моделей [8].

Рассмотрим примеры моделей космологических моделей на основе определенной связи между фоновыми параметрами инфляционных моделей и функциями, определяющими тип скалярнотензорной гравитации.

• 1.1.    Промежуточная инфляция

Модель промежуточной инфляции с действием (1) без материи рассматривалась в работе [23] на основе следующего соотношения между параметром Хаббла и функцией неминимальной связи ғ⑴=(乎).⑸

На основе соответствия физических потенциалов известным скалярно-тензорным теориям гравитации, которое формально выражается посредством следующих соотношений

V(0) - 3А2Ғ2(。)，

“(°)=—卜+2) 2，

Ғ(°) = А-2 [(2к — 1)(at - A)]2/(1-2fe), был восстановлен вид параметра Хаббла

H(t) = [(2左-1)(at - А)]1/(1-2*),(9)

где а > 0, А и к — некоторые постоянные.

Параметр Хаббла (9) соотвествует случаю промежуточной инфляции [8], различные режимы ускоренного расширения ранней Вселенной в зависимости от выбора постоянной к рассматривались в работе [23].

Рассмотрим производную параметра Хаббла a [(2人-1)(血-人)]1/(1-2*) (2k — 1)(a力—人)

При условии (2k — 1)(a 力 —A) >  0 получим Н <  0.

Рассматривая условие завершения инфляционной стадии на основе относительного ускорения расширения ранней Вселенной

-=Н² + Н = 0, а

получим следующее время завершения инфляционной стадии

i

A   (a) 2(^-)

& 二 a + (2k — i).

Таким образом, данные модели имеют выход из стадии инфляции.

На основе наблюдательных ограничений на параметры космологических возмущений найдены следующие ограничения на значения постоянных параметров модели

A2 < 6.7 X 1О-10,                                         (13)

k < 1.                                                      (14)

Также было отмечено, что любые будущие наблюдательные ограничения не носят принципиального характера для верификации данных моделей, а связаны с уточнением значений данных констант.

В качестве примеров рассмотрены инфляционные модели на основе гравитации Бранса-Дикке, индуцированной гравитации, неминимальной связи и экспоненциальной связи скалярного поля и кривизны [23].

• 1.2.    Модель степенной инфляции

Другой тип инфляционных моделей на основе действия (1) рассматривался в работе [24]

f=1--Ъ， где безразмерная константа 7 > 0.

При квазиэкспоненциальном расширении ранней Вселенной параметр расхождения с гравитацией Эйнштейна 7/а2«) быстро убывает, и к моменту пересечения радиуса Хаббла космологическими возмущениями модель становится неотличимой от случая ОТО. Как следствие, параметры данных космологических моделей практически неотличимы от случая гравитации Эйнштейна.

В данной работе рассматривался параметр Хаббла

Н ⑴ = mt^-1,                                   (16)

что приводит к расширению по степенному закону

-(t) 〜严.

Условие равенства нулю относительного ускорения (11), в данном случае, приводит к соотношению m =1. Таким образом, модель степенной инфляции не соответствует выходу из режима ускоренного расширения без привлечения дополнительных физических процессов, которые должны учитываться в уравнениях космологической динамики. Тем не менее, на основе предложенного подхода можно рассматривать различные режимы ускоренного расширения ранней Вселенной.

• 1.3.    Модель экспоненциально-степенной инфляции

В работе [25] рассматривались космологические модели на основе скалярно-тензорной гравитации с функцией вида

^{F (}" = ( 1 + 三) •                                     ( 18 )

Также рассматривался параметр ХабблаОО

Н ⑴ =А + mt-1,

который соответствует экспоненциально-степенному закону роста масштабного фактора a⑴〜严eм

Параметр А может быть как положительным, так и отрицательными, однако только для отрицательных значений А решение (20) может описывать Вселенную с конечной по времени инфляционной стадией эволюции. В работе [25], в которой была предложена эта модель, случаю А < 0 уделяется особое внимание.

Рассмотрим для метрики (20) относительное ускорение

Q := ^a = [「 А%² + 2Am 力 + m(m — 1) ] .                       (21)

a     t²

Требование наличия ускорения в расширении Вселенной означает, что относительное ускорение Q > 0. Корни квадратного уравнения

A²t² + 2Amt + m(m — 1) = 0

_        9

равны

—m + у^     —m — ^/m t1 = —А —, t2 = —А—

.

При А > 0 очевидно, что t? < 0. Чтобы момепт времени ti был положителыіым ti > 0 необходимо потребовать 0 < m < 1. При этом имеем замедленное расширение Вселенной (Q < 0) до момента ti и ускоренное расширение (позднюю инфляцию) при t > t> Отметим, что Вселенная всегда расширяется, так как Н всегда больше нуля в силу справедливости неравенства 岸 > —А при положительном А.

Случай А < 0 озиачает, что t? > ti и t? > 0 всегда. Если ti > 0 (при m > 1), то имеем две стадии ускорения Вселенной. Заметим здесь, что условие Н > 0 выполняется в ограниченном течении времени, а именно, до момента tCont =—受，после которого начинается сжатие Вселенной. Таким образом, при заданных параметрах, Вселенная претерпевает раннюю инфляцию при t < ti, затем расширяется с замедлением до момента сжатия tcont- Далее начинается замедленное сжатие, которое переходит в ускоренное после момента времени t?.

Вторая возможность ti < 0 (при 0 < m < 1). Вселенная замедленно расширяется до момента t cont после которого начинается за медленное сжатие до момента t?, которое ускоряется после этого. Таким образом, здесь отсутствует инфляция.

Определим параметры медленного скатывания на стадии инфляции

_ Н m

^Н2   (m + At)² ，

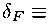
F    с

= —2з

Н F

6 三- -丄 =—¹V ， 2НН m + Xt

то есть параметр медленного скатывания е возрастает.

Далее запишем условие завершения инфляции как е = 1, что эквивалеiitiio условию 5 = 0. Для момента времени, когда это происходит, получаем m  ^/m

匸 а а 丄

Момент времени 七, соответствующий △ № хаббловских увеличений масштабного фактора до конца инфляции, является решением уравнения

△ N = т ln

+人（方 1 -七）.

Уравнение можно упростить, введя величины

72 =-凡 2,

丁 i =—凡 1 = m - ， m.

В терминах этих величин уравнение принимает вид

△ N = m ln

7 1 + 丁 2.

Для каждого значения т > 1 имеется свое решение. Это решение можно выразить через 1У- ( } ) упктппс ) Ламберта ：

丁 2 = -т • Wo

(^-( ^{1 -}白)

e ^- （ ^{1 -}金 ） e ^- 甯） ,

где Wo(x) - основная W- ( J ) yiiKTniH Ламберта.

Рассмотрение параметров космологических неоднородностей, сгенерированных на стадии инфляции, присутствует в работе [25]. Осветим основные этапы немного более подробно. Основные формулы приведены в работе [25], они полностью согласуются с результатами работ [13], [26].

Спектральный индекс скалярных неоднородностей подсчитывается как

几 § - ¹ = ^-2е - 6 q ，    6 q 三 Hq⁷

где

с   2H² - нН

='(н 2 + Н )2

и подсчет выполняется в момент пересечения волной неоднородностей горизонта, за △ TV хаббловских увеличений до конца инфляции.

Используя F = Н ²/Х² и уравнение (19), получаем

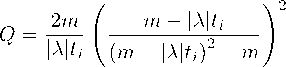
Подстановка уравнений (23) и (31) в уравнение (29), в терминах % дает

/-1

1       1

m 1 —弓/ m

4т і /т m (1 — ті/m)² — 1

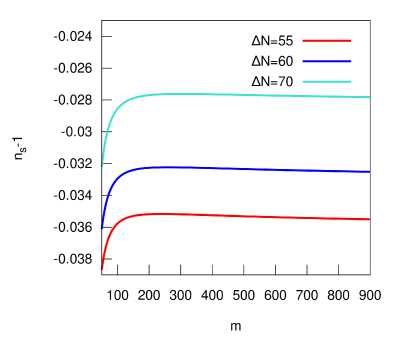
В силу выражения (27), это уравнение позволяет найти спектральный индекс как функцию параметра т. Соответствутоттпіп rpa ( J ) iiK представлен на Рис. 1а. Из гра ( 1 ) ика видно, что все ^значения спектрального индекса скалярных неоднородностей т > 50 согласуются с ограничениями на спектральный индекс. Наилучшее согласие достигается в области 60 < т < 100. При этом все условия режима медленного скатывания соблюдаются.

Для скалярно-тензорного отношения г основным выражением является г = 16es

q

¹⁶ 声

Для рассматриваемых моделей, в терминах ті, выражение для этой величины можно записать в виде

г

32ті /т

(т (1 — Ті/т)² — 1)

а

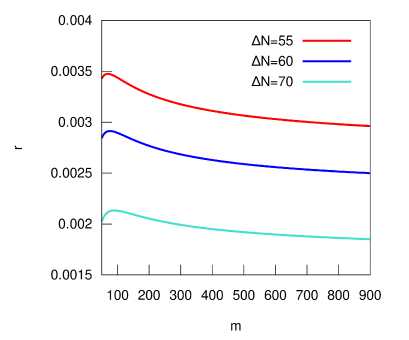
Рис. 1. Величина n_s — 1 (а) и скалярно-тензорное отношение г (Ь) как функции параметра т на интервале (50,900) при трёх значениях ATV.

b

Отсюда, в частности, при т = 100 и △№ = 60 получается 丁 = 0 . 00289. Видно, что это модели с экстремально низким скалярно-тензорным отношением, и потому удовлетворяют наблюдательным ограничениям. График зависимости г(т) представлен на Рис. lb.

Также, в работе [27] были получены следующие выражения параметров космологических возмущений в терминах параметров медленного скатывания г = 32т83 (mb — 1),(35)

ns — 1 = 3b — 5mb2.(36)

Исключая из данных выражений параметр b, получим явный вид зависимости тензорноскалярного отношения от спектрального индекса скалярных возмущений

質=625m2 ](-3 +，20m(1 - ns)+ 9)(7 +，20m(1 — ns) + 9)] .

Также, рассмотрим предел зависимости (37) при m — х, что дает

丁8 = 32 (1 - ns)2 .

Отметим, что для случая m — 0 из выражения (37) следует, что г = 0.

Для n_s = 0.9663 — 0.0041 = 0.9622 из выражения (38) получим т^ = 0.0018, что соответствует наблюдательному ограничению (3).

Осталось проверить ограничения на значения параметра 人.Здесь можно использовать соотношение н2       1   ((m — |入质)2 — m) 9            Q

『 s = 荷" 1^m -ж2 = 2.^{1 x 10-9}.             ( 39 )

При m = 100 полу чаем 『 _s 心 69.998A² = 2.1 x 10^-9. Этому условию соответствуют достаточно малые значения параметра А. Они гарантируют, что космологические возмущения покидают горизонт при временах много больших планковского времени.

Таким образом, для рассмотренного класса моделей существует область параметров, в которой модели хорошо согласуются с наблюдательными данными.

• 1.4.    Модель с квази-экспоненциальной инфляцией специального вида

В работе [27] представлен еще один класс моделей вида (1), которые допускают вакуумное космологическое расширение по закону

。⑴ 〜 e^xte~^ /².                                       (40)

Такие модели получаются при условии (5) и дополнительном анзаце

Н ⑴ =А - & А > 0.

При А — " > 0, т.е. при достаточно ранних временах, имеет место расширение. На больших вре менах, при

А

力 > ^ cont — W ,

происходит сжатие вселенной. При временах

力 < 力 1 ^— 力 cont--7W

характер расширения имеет инфляционный характер (d >  0). Более того, при 力 <  0 реализуется супериифляция (Н > 0). Таким образом, это модели, в которых есть окончание инфляции. Момент времени 力 i также примем за конец инфляции в режиме медленного скатывания. В тот момент времени е ( 〃) = 1. Поскольку эволюция в таких моделях заканчивается вечным сжатием, при отсутствии современной инфляции, то модель может быть применима только в очень ранней вселенной, когда еще можно не учитывать взаимодействие с материей.

В работе [27] определено несколько наборов функциональных зависимостей V (0), F(0) и ®(0), приводящих к одним и тем же уравнениям (5), (40) и (41). Получены выражения для P_s, n_s, г. Тем не менее, сравнение предсказаний теории с наблюдательными данными, присутствующее в работе [27], желательно провести максимально аккуратно и подробно.

Подсчёт параметров космологических возмущений основан на прежних уравнениях (29), (30), (33). Вычисление в нашем случае даёт

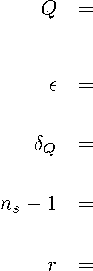
₂ f    ( а -也 )2

人 ² ( ( а - €^ ₄)² - €) ²'

W

( 人 -也^{) 2}

― 2g +         4g

(a -也 ⁾²   (a - gti ⁾² - ^g

-      4g

( а -& ) ²-и

32g2

((а - gti)2- g)2， где ti，так ii прежде. обо：зиа.чает момент пересечения волной тіеодтюродтюста горігзонта.

Полученные уравнения удобно переписать, используя безразмерное время

Ti 三 У!ti.

В частности, получаем

/-1

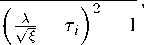
г

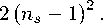
Видно, что скалярно-тензорное соотношение оказывается квадратичной функцией от ^s —1 ・ причем такой, что если ns — 1 удовлетворяет наблюдателыіым ограничениям, то и г им тоже удовлетворяет.

Осталось посчитать значения n_s иг для неоднородностей на космологически значимых масштабах. Надо посчитать эти величины для волны, пересекающей горизонт за ATV хаббловских расширений до конца инфляции. Момент времени 七， когда это происходит, можно найти из уравнений

V 三 / Hdt = А 力 — ； "² + const,

Обозначив

△ ^V = ^Ati — 2 "1 — \і_г + 2 "2.

А s =    ,

避'

и проделав простые преобразования, получим квадратное уравнение

К — ®)2 = 2AV + 1.

Подставка этого выражения в (50) даёт

ns — 1

△ V^.

Для первого параметра медленного скатывания аналогично

「_      1

с = 2AV + 1.

Надо отметить, что в выражения (56) и (57) входит только ATV, явная зависимость от А и £ отсутствует.

Выражения (51) и (56) оказываются довольно чувствительными к количеству е-фолдов между пересечением волной неоднородностей горизонта и окончанием инфляции. Полагая ATV = 60, получаем ns — 1 仁—0.033, г 仁 0.00218,

в прекрасном согласии с наблюдательными данными.

Осталось только проверить возможность выбора подходящего А. Эту величину можно выбрать так, чтобы выполнялось условие

V s

Я 2

А2 . о                   с

8*Q —并攻= ² 」 X ^{10 -} 9.

Таким образом, данная модель также удовлетворяет наблюдательным ограничениям на значения параметров космологических возмущений.

• 1.5.    Космологические модели, неотличимые от эйнштейновских на уровне линейной теории возмущений

В работе [28] представлен специальный класс космологических моделей с действием вида

S = 2 / ^d4т ^— ž [ Ғ ( ^{0, R)} ― 3 ( ⁰⁾.g"" d ^ °d_v ⁰ ― 2V ⁽⁰⁾ ] ,

где F ( 0, 为= A + / ( 0m + 式 0 ) i^в ， фуикция / ( 0 ) определяет взаимодействие скалярного поля и скалярной кривизны R и £ ( 0 ) — функция взаимодействия поля со скаляром Гаусса-Бонне Ғ^_в = Rs Rs — 4R h 〃 R h 〃 + R².

Особенностью представленных теорий является тот факт, что параметры их космологических возмущений с очень высокой точностью совпадают с параметрами в космологических моделях на основе эйнштейновской гравитации для функций вида

/ ⑴

^p ST ^),

s- 容 exp 3, a0    V ^hФ /

g

&GB ^H2 ,

Q gb

ĆJ ⑴ =1

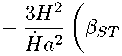
斶歹 ^{2 exp}

2q gb 、

十 d³ ,

з ( ° ) = ^{1 +} ； ( Д) ^exp

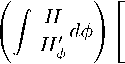
А , 2 ^a GB

P ST +--5— exp

Л

,

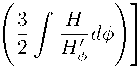
где a 。— некоторое начальное значение масштабного фактора, & gb и P st — константы связи скалярного поля со скаляром Гаусса-Бонне и скалярной кривизной соответственно.

Фоновые космологические решения, в данном случае, совпадают с решениями, полученными на основе гравитации Эйнштейна. Также, на сегодняшнем уровне точности наблюдений, в линейной теории возмущений, данные модели неотличимы от соответствующих космологических моделей в рамках общей теории относительности.

Заключение

В данной работе рассматривались скалярно-тензорные теории гравитации, подразумевающие возможность построения актуальных космологических моделей. Показано, что для специального выбора соотношений между функцией неминимальной связи и параметрами фоновой динамики возможно построение верифицированных моделей космологической инфляции. Также было показано, что предложенный подход можно обобщить на случай моделей с неминимальной связью скалярного поля и скаляра Гаусса-Бонне.

Отметим, что представленные случаи динамики расширения ранней Вселенной, которые использовались для построения и анализа инфляционных моделей, не исчерпывают возможностей применения предложенного метода. Развитие и обобщение предложенных методов на случай различного вида фоновой динамики и различные эпохи эволюции Вселенной является перспективным направлением дальнейших исследований.