Собственные линейные колебания цилиндрической оболочки в упругой среде

Собственные колебания стержней и оболочек в упругой среде рассматриваются в работах [7; 10; 11]. В данных исследованиях окружающая среда стержней и оболочек заменяется упругими пружинками, т.е. при расчете учитывается коэффициент жесткости пружин. В работе [5] рассмотрены собственные колебания сферических оболочек в упругой среде, которые удовлетворяют уравнению Ламе (для оболочек и упругой среды). Сделан анализ полученных численные результатов. В настоящей работе, в отличие от известных работ рассматриваются собственные колебания цилиндрических оболочек с учетом условия излучения Зоммерфельда на бесконечности.

Постановка задачи

Достаточно протяженная цилиндрическая оболочка и окружающая ее среда сводятся к плоской задаче динамической теории упругости. В предположении обобщенного плоско-деформированного состояния уравне-

ние движения окружающей среды в смешениях имеет вид [8]

ρс

ρс

д2 иД

θ

д t2

7 дд

+ ² Мс •

д a_z , (1) д r

где

_А = 1 ^{д (} ги _г ) ₊ 1 ^д и _в r    д r     r дд

2 ® _z = ~

r

д ( ru _e ) д u _r д r     дд

здесь λ _с и µ _с – модули упругости окружающей среды оболочек, называемые постоянными Ламе ; ρ с – плотность окружающей сре-

^^          ^

ды, U = u_rK_r + и _д К _д - вектор перемещения

точек среды; K _r и K _θ – единичные векторы. Поставленная задача для окружающих оболочек среды решается в потенциалах перемещений

д r r д О

r д д д r

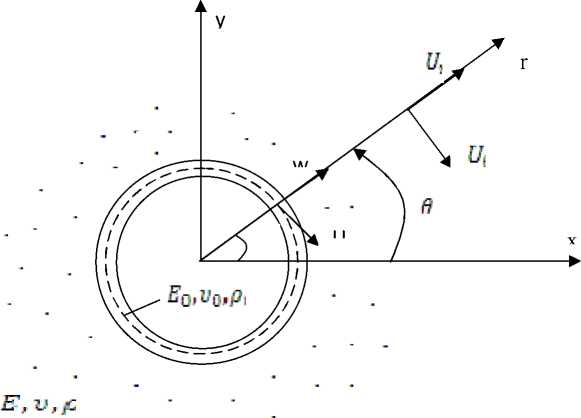
Расчетная схема

Потенциалы ϕ и ψ удовлетворяют волново- _где

му уравнению

V 2 (p

1 д ² p

C^ д t2

2        2, с 2 д t

x1

^— & г О

r = R + h /2 ^P o ^h o

д2 и. lt^;

где    c2 = (Ac + 2^C)/Pc,c22 = Pc /Pc.

Уравнение движения цилиндрических оболочек на основе гипотезы Кирхгофа–Лява, при плоской постановке задачи имеет вид

x 2 = ^— & r r = R + h /2 - P o h o

д2 w.

д2 u дw   R2

+=

дО2  дО    B

b ²

h o ²      _;

12R2

ди г.2 Г б4 w , д2u +b + 2

дО    [de4   дО2

У + w

J

B

E h oo

1

—

v

o

& ^re l r = R + h /2

1 д 2 p      1 д p r д О д r r 2 д О

1 д ² щ        д ( 1 д щ

--— r-----1-- r 2 д О 2 д r [ r д r

J r = R + h /2

σ

rr

r = R + h /2

д ² p д ( 1 д щ д r ² д r [ r д О

r = R + h / 2 ,

V ² p

1 д r д r

д p У r д r J

+

1 д ² p

Гр

Здесь R – радиус срединной поверхности оболочки; ρ0 – плотность оболочки; v – коэффициент Пуассона оболочки; E0 – модуль уп- ругости оболочки; σrr и σrθ – нормальные и касательные, составляющие реакции со стороны окружающей среды.

Контакт между оболочкой и окружающей средой может быть жестким, т.е. выполняется равенство соответствующих перемещений и напряжений :

и \           = иа \          ,

Ir = R + h/2       0 \r = R + h/2, w\r = R + h/2 = ur|r = r + h/2.      (4, а)

Для скользящего контакта w|r=R + h/2 = urlr = R + h/2,

⁶⁷ r О I r = R + h /2 = 0.     (4, б)

Решение системы дифференциальных уравнений (1) и (3) удовлетворяет на бесконечности (при r → ∞) условию излучения Зоммерфельда [4]:

lim < p = 0,                (5, a)

r ^^

lim( д/ r ) | — + i a^\ = 0 ,    (5, б)

r^x     I drJ lim^ = 0,            (5, с)

r ^^

lim(7r) [^ + iev ^ = 0, (5, d) r ^X       к drJ где α и β – волновые числа;

^a =— , ^e = —c c = ( Л + 2Я )/ P c , c 2 ² = я / Р с .

c1

Волновые числа могут быть комплексными числами, мнимые части характеризуют затухание, т.е. убывание с расстоянием амплитуды волны со скоростью c/Rе α [2; 5; 9] (здесь Reα – реальная часть волнового числа α). Условия (5, а) и (5, с) называются условиями конечности, а (5, б) и (5, д) – условиями излучения.

Методы решения

Решение волнового уравнения (2) и (3) будем искать в виде

^u ^ (V. (R) ^ ' sin nO ^ w =X n=o w. (R) cos nO — i-t .e Ф фп (r ) cos nO ,       (6) V j Vn (r) J ^sin nO j где a = сок + iaI — комплексная собственная частота; Vn (R),Wn (R) – амплитуды перемещений оболочки; фn (r),ψn (r) – амплитуды потенциалов перемещения удовлетворяют уравнениям Гельмгольца

V ² ф_п + ^{a 2} ф = 0, V ² v „ + ^{e 2}v_n = ^0.

Решение уравнения Гельмгольца в цилиндрических координатах выражается через функции Ханкеля первого и второго рода n- го порядка:

Ф. = A n 1 H^ar ) ⁺ B n , H^ar ),

V n = A 2 H^ Pr ) + B „ 2 H£( Pr ),      (7)

где Ani (j=1, 2) и Bni – произвольные постоян- ные, которые определяются из граничных усло вий (4) и (5); H.1 (Kir), Hn2)(Kir) — функции

Ханкеля 1-го и 2-го рода n -го порядка [3].

Рассмотрим частное решение

Ф п = Re [ e- - H 0 ¹ ) (ar ) ] .

(8, а)

При возрастании r для больших аргументов

H ⁽¹⁾ ( αr )

функции 0       справедлива асимптоти ческая формула [8]

H 0" (^m > «^ ^{[1 +} O ⁽ r ⁴ 4   (8, б)

O ( r ^a )       о

Через обозначим такую величину

y y, что отношение rk остается ограниченным при r > X. При учете (8, б) формула (8, а) примет следующий вид:

Ф 1 = Re

π

2 i (arat ) e ⁴

πα r

■ 1 + O ( r -' ) ]

cos ω πα r

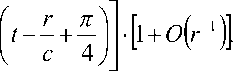
Здесь мы имеем дело с расходящейся волной, распространяющейся в направлении возрастания r со скоростью с. Также можно показать, что вторая волна ф, = Re; -“H02) (ar)] является сходящейся, т.е. не имеет физического смысла.

Из условий Зоммерфельда следует, что H_n ⁽²⁾ ( K_ir ) описывает сходящую волну, поэтому при r ^ от будет равно нулю ( В _n i = В n2 = 0).

В качестве примера рассмотрим собственные колебания упругой среды с цилиндрическим неподкрепленным отверстием. На границе r=R вставим условия свободного от напряжения, т.е.

^ rr\r = R = ^ r d I r = R = ⁰-          (9)

После подстановки (6) с учетом (7) в граничные условия (9) получим систему алгебраических уравнений с комплексными коэффициентами. Для того чтобы система алгебраических уравнений имела нетривиальное решение, необходимо, чтобы основной определитель был равен нулю. Элементы основного определителя содержат ω. При равенстве основного определителя нулю получим трансцендентное уравнение относительно частоты ( ω), которое описывает собственные колебания упругой среды с отверстиями:

Dn = xHn-i [(n 2 — 1)yHn-i (У) — (n 3 — n + У 2/ 2)Hn (У)]—

- Hn(x)[(n3 - n + У2/2)yHn-1(У) -(n2 + n - У2 / 4)У2Hn (У)], где x = aR(p /(1 + 2p))1/2; у = aR(p / p)1/2; 1 и µ – коэффициенты Ламе; ρ – плотность материала.

Уравнение (10) после некоторых преобразований можно написать в следующем виде:

( n ² - 1) F ( x ) F ( y ) - ( y 2 /2)F ( x ) + + F(y) + n ² - ( n ² - y 2 /2) 2 = 0,

где F ( x ) = xH 1 (x )/ H_n ( x ), n = 1,2,3....

Частотное уравнение (11) решается численно, т.е. методом Мюллера [2]. Корни трансцендентного уравнения (11) являются комплексными числами, которые состоят из двух частей: реальные (Reω) и мнимые части (Im ω). Реальные части корня описывают собственные частоты механической системы, а мнимые части описывают коэффициенты демпфирования (коэффициент затухания) [6; 12]. Результаты расчетов при n > 0 (v = 0,25) собственных колебаний приведены в табл. 1.

Как видно из табл. 1, с увеличением числа волн по окружности соответствующие реальные и мнимые части комплексных частот возрастают. Частотное уравнение (11) зависит только от параметра ν (коэффициент Пуассона).

Таблица 1. Корни трансцендентного уравнения в зависимости от n (числа волн)

ω	n=0	n=I	n=2	n=3
ω 1	0,4529D+00 -i0,47651D+00	0,10927D+01 -i0,76538D+00	0,19075D+01 -i0,89782D+00	0,27565D+01 -i0,99155D+00
ω 2	–	–	0,28621D+00 -i0,17852D+00	0,72325D+01 -i0,32283D+01
ω 3	–	–	0,404607D+00 -i0,178552D+00	0,12307D+00 -i0,22283D+00

⁽ 1)    ² P c V Л - - ^{i a t}

^ R =      X 10 A 0 e ,

R

С увеличением коэффициента Пуассона в пределах 0 < v < 0,4 реальные и мнимые части комплексной частоты изменяются до 27 %.

Таким образом, на основе приведенных исследований выявлено, что рассматриваемая механическая система имеет дискретные комплексные собственные частоты.

Далее рассмотрим осесимметричные собственные колебания цилиндрических оболочек, находящихся в упругой среде. Дифференциальное уравнение, описывающее осесимметричные колебания цилиндрической оболочки, имеет вид [1]:

1 2 д w д w

b —+22—— + w + w =

[д в⁴    де²

7

-

^{( 1 -} v о² )

E о h о V

7 д w

Р 0 h O^p + °R д t        7

,

X 10 =- d 1 ^ 1 H 0 ^l)( Q _l) + ^ H №),

Ц = aR =— ; d 1 = -1- v -, b ² = h ²/12 R ², c 1           ^{1 - 2} v c

А 0 – амплитуда перемещений.

Подставляя (6) и (4, а) в (12), получим систему алгебраических уравнений с комплексными коэффициентами. Для того чтобы система алгебраических уравнений имела нетривиальное решение, необходимо, чтобы основной определитель был равен нулю. Тогда для определения ω получим трансцендентное уравнение (условия скользящего контакта):

^h 2 ^y 1 n ^{- Z} 0 ( ^ 0 ) ^X 1 n ^h 2 ^y 1 n ^{- Z} 0 ( ^ 0 ) ^X 1 n   Q

^Z 1 n                    ^X 2 n

где где

h 2 = h 0 ;   y 1 n = nH Mt Ml Hi ( Q ) ;

R

b l = E ( 1 - v 2 ) / ( E 0 ( 1 + v )) ;

где

+

a 01 +

^d 1

^ h 2 ^V 2

+

Г b 1 d 1 L 1 ¹ к 2 h 2 V 2 J

J

L 1 = n E 1 (1 + V 1 )(1 - 2^/(1 - v 1 ).

a n 2 = n ’; d 1 = E 0 h 0 (1 -v 0 );

• X1. =(- d1Q + an2 Н^МкМ);

Для существования ^— = ⁿ ₀ ⁺ i « I комплексных собственных частот необходимо вы-

X

2 n

= an 2“, 1 H M 2 ) +n 2 H n + ( n 2 ) ;

к 2 J

.y 2 n = nH^ ) +« 1 H" ( « 1 ) ;

полнение условия:

a ₀₁

/v1 >

b + dbL

к h2V2 J  к 2h2V2 J

«о =—R;

0    _{C 0}

z ₀( Q 0 ) = m[(q 2 v 2

Cо = EE/Jn, ,

^{- a}n 1 ) ^{- n 2 /( n} 0 ^V 2 ^-

v ₂ = 1 - v ₀ ;    a _n1 = b ² ( n ² - 1 ) + 1;   « 2 = Q ₁

' C1'

к ^C 2 J

С 0 – скорость распространения волн в стержне; Е 1 = Е/E 0 .

Осесимметричные колебания цилиндрической оболочки (для жесткого контакта), частотное уравнение описывается выражением

Если это условие не выполняется, тогда для цилиндрической оболочки будут существовать мнимые собственные частоты ( Q I ). Для выполнения первого условия модуль упругости Е ₁ должен удовлетворять неравенству E >^{( 1 + v} 1 ) ( ^{b 2 + 1} ) h ^{2 (} П 2 ^{+ ( 1 -} v -VX¹ 2 v -)^{1 ( 1 v} 2 ^{)- 1 )} .(13)

Кроме того, для η выполняется следующее условие:

- 1

h 2 ( « 2 v ₂ - a _{n 1} ) + b ₁ - b ₁ d ₁ Q ₁ H¹ ( Q )/ H^( & ) = 0.

n <(1-2v)(1 v02)-1 h0a„(11 v)n(1-2v)-1| E1 . к E J

Если использовать асимптотическое выражение функции Ханкеля при |«| >  ¹ , то для нулевого и первого порядка получим выражение комплексных собственных частот:

— = - i

b 1 d 1 L 1 ₊ 2 h ₁ v ₂

Численные значения осесимметричных ( n =0) собственных частот приведены в табл. 2 ^{( n} =0,1; ^V 1 = ^v 2 = ^0,14 h 0 =0,025). На основе полученных численных результатов приходим к выводу, что при Е 1 = Е/E 0 > 0,21, т.е. реальные части собственной частоты обращаются в нуль, а поведение мнимых частей остается неизменным.

Таблица 2. Зависимость собственных комплексных частот от Е

ω	Е 1 =0,03	Е 1 =0,0 85	E 1 =0,12	E 1 =0,15	E 1 =0,21
Re ω	1,3308 - 10 - 1	0,3276 - 10 - 1	0,2670 - 10 - 2	0,41665 - 10 - 3	0,616810 7
Im ω	- i - 0,9767 - 10 - 2	- i 0,5891 - 10 2	- i 0,1776 - 10 - 2	- i 0,9391 - 10 - 3	- i 036910

Выводы

• 1.    Нами была предложена постановка задачи собственных колебаний цилиндрических тел находящихся в деформируемой среде. Задача сводится к нахождению тех — = Q ₀ + i Q I ( Q ₀ - реальная и Q i - мнимая части комплексных собственных частот), при которых система уравнений движения и условия излучения имеют ненулевое решение в классе бесконечно дифференцируемых функ-

• ций. Было показано, что задача имеет дискретный спектр.

• 2.    Из обсуждения результатов установлено, что с увеличением модуля упругости и коэффициента Пуассона соответствующие собственные частоты механической системы медленно увеличиваются. Собственные частоты (Reω) и коэффициенты демпфирования (Imω) при скользящем и жестком контакте отличаются до 15 %, а при жестком контакте – более 15 %. С увеличением толщины оболочки собственные частоты увеличиваются до 10 %.