Соединение деревянных конструкций с МЗП на металлических накладках

Материалы из инженерной древесины, применяемые в строительстве, обладают различными достоинствами и недостатками [1]. Большое влияние на характеристики деревянных конструкций оказывают применяемые соединения. Современному инженерному и научному сообществу известны различные виды соединений деревянных конструкций, но разработка новых, более эффективных решений всегда актуальна [2-5]. Среди этих решений интерес представляют системы на металлических накладках и соединения с применением металлических зубчатых пластинах (МЗП).

Соединения на металлических накладках представлены на российском и зарубежном рынках в различных исполнениях. К рассмотрению в данной работе приняты изделия производства компании SHERPA, где была разработана своя оригинальная конструкция с множеством типов [6].

Разработка, представленная в данной статье, основана на исследованиях авторов T. Bogensperger и F. Hude [7]. Кроме того, учтены исследования, произведенные в работах Сюй Юня [8, 9]. В этих работах предложено оригинальное решение для соединений деревянных конструкций на металлических накладках с укреплением МЗП, представленная на рисунке 1.

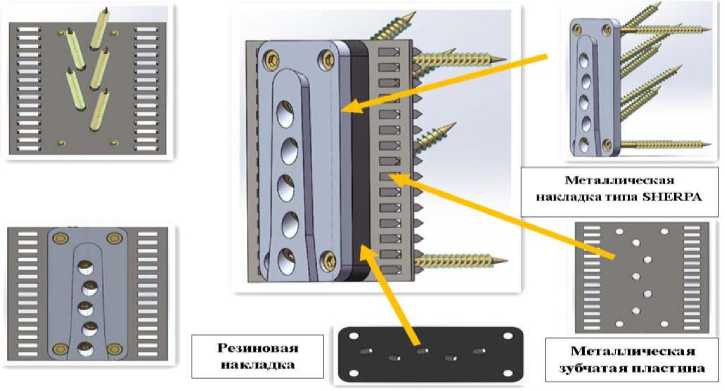
Рис. 1. Конструктивная схема соединения деревянных конструкций на металлической накладке с укреплением МЗП

Создана математическая модель расчета предложенного соединения. Несущая способность соединения:

для стеновой панели из CLT:

F v , k ,панель, sherpa = П * ( F v ,a, k ,1 + F 2, k ,1 + F 2, k ,2 + F 3 )                                  (1)

для балки из CLT и LVL:

F v , k ,балка, sherpa = n ’ ⁽ F v ,a, k ,1 + F 2, k ,1 + F 2, k ,2 + ^F3 )                                   (2)

для всего соединения:

F v , k , sherpa    min ⁽ F v , k ,панель, sherpa , F v , k ,балка, sherpa )

где

F , .

v ,a, k ,1

a

– несущая способность односрезного шурупа c укреплением МЗП под углом

к волокнам;

F l, k ,1

– вертикальная компонента от несущей способности шурупа на;

F 3

– несущая способность при смятии в гнезде металлических накладок под шурупы;

n – количество шурупов.

В целях повышения несущей способности соединения в настоящей работе предлагается вариант усовершенствования конструкции, представленный на рисунке 2. Положительный эффект достигается благодаря несущей способности загиба и улучшению способности металлической зубчатой пластины производить перераспределение усилий, воспринимаемых элементами соединения.

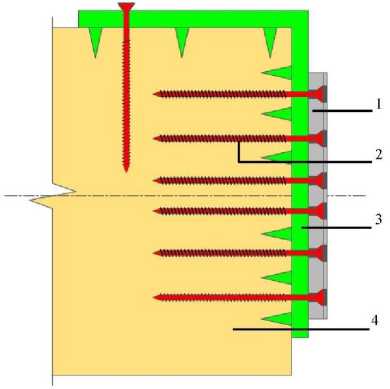
Рис. 2. Предлагаемая схема крепления металлической накладки с металлической зубчатой пластиной: 1 – металлическая накладка типа SHERPA; 2 – шурупы; 3 – металлическая зубчатая пластина; 4 – элемент деревянной конструкции

Несущая способность соединения принимается как сумма нагрузок, которую выдерживают его составляющие. Математическую модель, представленную в формулах (1-3), необходимо дополнить, чтобы учесть величину нагрузки, которую вос- принимает загиб металлической пластины. Работу этой части возможно представить отдельно, как балку на упругом основании, нагруженную на конце силой P0 и имеющей конечную l1 (рис. 3).

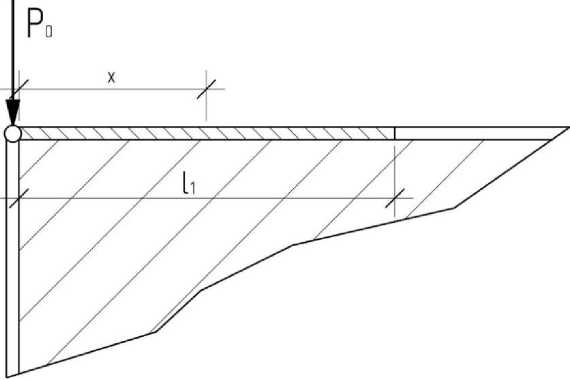
Рис. 3. Схема для расчета загиба МЗП как балки на упругом основании

Место сгиба пластины принимается в расчетной схеме шарниром, так как его жесткость пренебрежимо мала, поэтому момент, передаваемый от основной части, не учитывается. В монографии Глухих В.Н. и Черных А.Г. [10] подробно рассмотрено решение для балки на упругом основании конечной длины, нагруженной

сосредоточенной силой в начале координат.

Для бесконечно длинных балок, при ус-

ловии

K =β 4EI

, уравнения изгибающе-

го момента и поперечной силы будут иметь вид:

M ( x ) =

e — ^{в x}

—Posin Px

;

Q(x) = — e ^xP (cos вx — sin вx)

где

K = Kod

;

K – коэффициент жесткости упругого основания – сила отпора основания, приходящаяся на единицу длины нагеля при прогибе, равном единице.

K

0 – коэффициент постели;

b – ширина пластины.

EI – изгибная жесткость пластины.

При решении задач для балок конечной длины последовательными приближениями потребуются уравнения, подобные (4) и (5), и содержащие слагаемое с сосредоточенным M моментом 0 . Эти уравнения известны из теории расчета балок на упругом основании:

M (x) =

e ^{— e x}

P

[Po sin вx — вMo (cos вx + sin вx)]

Q(x) = — e ^x [Po (cos вx ~ sin вx) + 2вMo sin вx]

Полное выполнение условий достигается выполнением последовательных приближений по рисунку 5.

Уравнения для поперечной силы и изгибающего момента окончательно имеют вид:

_e ^{— в x}                _e ^в l i ^{- x} )

M ( x ) = —— P o sinв x ---—[— e ^в l ¹ P o (cosв4

— sin в l ₁) • sin в( l₁ ~ x ) —

— e ^{— в 1 1} P _o (cos в( l ₁ - x ) + sin в( l ₁ ~ x )) sin в l ₁ ] —

p ^{в x}

-—{— e -P ^{l 1} [— e -P ^{1 1} P o (cos в 4

— sin в l ₁ ) 2 + 2 e ^{— p 1 1} P _o sin² в4 ] sin в x —

— e ^{p l 1} [— e ^{p 1 1} P _o (cos в l ₁ — sinв l ₁)sinв l ₁ — e ^{в 1 1} P _o • (cosв l ₁ + sinв l ₁)sinв l ₁](cosв x - sinв x )};

Q ( x ) = — e ^{в x} P₀(cos в x — sinв x ) — e ^{в( 1 1 x} ) { — e ^{в 1 1} P_o (cosP l ₁ — sinв l ₁) •

• [cos в( 4 — x ) — sinв( 4 — x )] + 2 e "^{в 1 1} P sIrP 4 cosP( 4 — x )} —

— e ^{в x} { — e" ^{в 1 1} (cos в x — sin в x ) • [ — e" ^{в 1 1} P_o (cosP 4 — sinв 4 ) ² + 2 e" ^{в 1 1} P _o sin ² в 4 ] + + 2 e" ^{в l 1} [ — e" ^{в 1 1} P (cos в 4 — sin в 4 )sinP 4 — e "^{в 1 1} P (cos в 4 + sin в 4 )sinP 4 sin в x ]}.

В результате дифференцирования функции поперечной силы получается уравнение интенсивности усилий отпора. График для данного уравнения представлен на рисунке 4:

q (x) = Q‘(x) = 2PP0 [ e "P( l1- x){(-e-e 11 + 1)sinP 11 cosP( 11 - x) + +e-P11 (e-P11 sin в 1X sinP( 1X - x) - cosP 1X cosP( 1X - x))} +

+e-Px (cos Px + e -2P 11 {- sinPx sinP( 11 - x )(sinP 11 + cosP 11) + +sin2 P11 - sinP 11 cosP 11 (cosPx + 1)+cos2 P11 cosPx})].

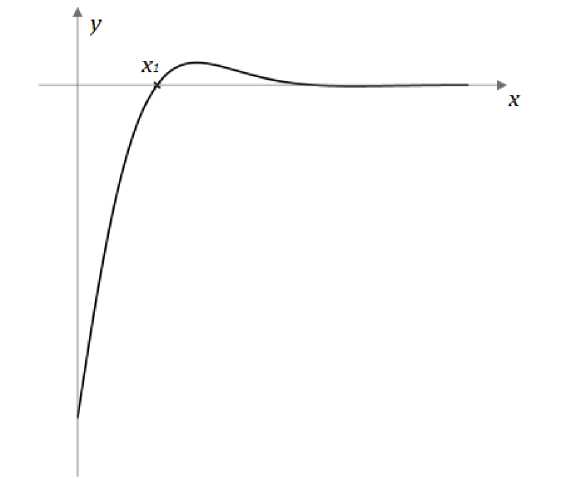
Рис. 4. Эпюра интенсивности усилий отпора под пластиной

Принимается гипотеза о том, что реакция основания равномерно распределена по ширине и неравномерно по длине. Тогда напряжение под пластиной принимает вид:

Jx1 q (x) dx о = —-----

xx • b

q^ = V (x)

При 0         уравнение полной несущей способности рассматриваемого соедине ния по условию смятия древесины имеет следующий вид:

P

см

Rcv90 • x1 • b

£x1 V ( x ) dx

Также следует учесть несущую способность по пределу текучести МЗП. При

M

max

P 0

= N

max

(эпюра моментов представлена на рис.5) получается уравнение:

y , k

РМЗП = TV max

где

f

^{y , k} – предел текучести МЗП; W – момент сопротивления МЗП.

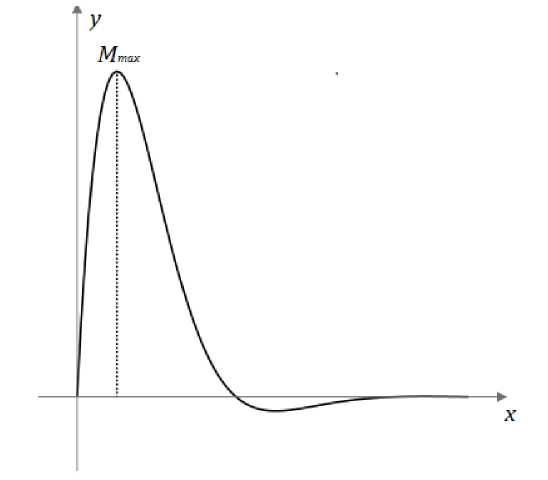
Рис. 5. Эпюра изгибающего момента

Несущая способность загиба МЗП:

P = min <

Р см

^ P M3n

Полная несущая способность усовершенствованного соединения:

F = F , , +P усов       v , k , sherpa

Предложенный вариант усовершенствования конструкции МЗП в соединении на металлических накладках позволяет более широко применять данный тип соединений в конструкциях из инженерной древесины. Полученные уравнение интенсив- ности усилий отпора основания под балкой на упругом основании и уравнение полной несущей способности усовершенствованного соединения возможно применять для расчета данных соединений.