Solving parabolic-hyperbolic type differential equations with spectral analysis method

In a rectangular domain A = {(x, С) : 0 < x < 1, —a < С < в}, we consider the following parabolic-hyperbolic type equation

<

L V (x,C ) = <

∂V ∂ξ

-

∂ ² V

—У + q^(x)V = 0, ∂x ²

∂ ² V

∂ξ ²

-

∂ ² V

—+ q^(x)V = 0, ∂x ²

С > 0,

С < o,

where a, в are positive real numbers. In the domain A we find the solution V(x, С) that satisfies the conditions

V (x,C ) G ^ = C ( A ) П C 1 (A) П C X ( A ) П C 2 (A - ) П C ^ A)

V (x, — a) = ^(x), 0 <  x <  1, V x (0,С) = 0,   —a <  С <  в,

(2) (3)

VW) — V(U) + V(0Л) = 0, -a <  ( <  в,

where A - = АП { ^ < 0 } , A + = А П { ^ > 0 } , and ^(x) is a given sufficiently smooth function.

In physical problems such as plasma physics, the diffusion process of particles, models of money accumulation in economics, heat dissipation in a heated thin rod, one may encounter mixed type differential equations (see [1–5]). Equations of this type are commonly found in problems related to wave propagation, heat conduction, and fluid dynamics. Some specific applications include: modelling sound waves in fluid flow, describing the transport of a quantity with both diffusive and advective properties, describing the temperature distribution in a material with both heat conduction and fluid flow, describing the density of traffic with both diffusive and advective effects.

The study of mixed-type equations has been a topic of considerable interest among authors in the literature, with a multitude of investigations exploring various facets of Tricomi-type problems. The ongoing pursuit of knowledge in this domain is contingent upon the specific region and the intrinsic characteristics of the problem under examination (as evidenced by the extensive literature cited in [6–14]). The Tricomi equation describes certain types of flow patterns in fluid mechanics, particularly in the study of irrotational compressible flows. It has applications in aerodynamics, where it helps model the behaviour of air around certain types of wings and airfoils. The equation also appears in mathematical physics, where it is used to model various physical phenomena involving wave propagation and fluid dynamics. In the [2] study, the flow of gas in the channel is expressed by the d² u      л                                                                du j .

wave equation —— = aAu and outside the channel by the diffusion equation — = bAu, dt2                                                                dt where a, b are physical parameters and A is the Laplacian. Continuity is required at the boundary of the channel. This model expresses a physical process in a two-part space connected by two equations and conjugate conditions at the boundary.

In [3], the system of first-order differential equations is defined in the intervals [0, l] and [l, to ), respectively, depending on the presence or absence of losses in the process of propagation of electric waves in the semi-infinite line. This system of equations is reduced to hyperbolic-parabolic type equations with the same conditions. Therefore, many mathematical models are encountered with mixed type partial differential equations depending on different processes.

In [15], the motion of the fluid in the electromagnetic field is analysed and it is shown that it is expressed by the boundary problem for the hyperbolic-parabolic type equation in multidimensional space.

Various methods are used to prove the existence and uniqueness of the solution of initial-boundary problems for mixed-type differential equations. For example, the maximum principle or integral identities can be used for uniqueness and apriori evaluations or integral equations can be used for existence. This study demonstrates the existence and uniqueness of the solution to the boundary value problem (1) – (4) the application of spectral analysis techniques, as outlined in the studies referenced in [13, 14].

1.    Spectral Problem

We want to find a non-zero solution of the boundary value problem (1) – (4) in the form V (x, £) = Z (x)Q(C)• Substituting this expression in equation (1) and boundary conditions

(3), (4) we obtain the spectral problem for Z (x)

—Z ‘‘ (x) + q(x)Z (x) = XZ (x),(5)

Z ‘(0) = 0,(6)

Z ‘(1) — Z (1) + Z (0) = 0,(7)

and for Q(^), the ordinary differential equation

Q‘«) + XQ«) = 0, 0 < ( < e,(8)

Q’’«) + XQ«) = 0 — a < ( < 0,(9)

where λ is a complex parameter. The boundary conditions (6), (7) are regular in the Birkhof sense, even strongly regular (see [16]). The root functions of the boundary value problem (5) - (7) form a Riesz basis in the space L 2 (0,1). The eigenvalues of the boundary value problem (5) – (7) are simple and form two infinite sequences (see [16]):

X _ti = (2kn) ² [1+ O^ 1,

^X k,2 = [^{(2k + 1)n]} 2

1+■>

the eigenfunctions corresponding to these eigenvalues are

Z _k,1 (x) = cos2knx + O

(9-

k 4 № ,

Z _k ,2 (x) = cos(2k + 1)nx + O

(a-

к ^ to.

It is known that since the functions Z _k (x) = { Z _k,1 (x), Z _k, ₂ (x) } form a Riesz basis, there is only one sequence { Y _k (x) } biorthogonal to them. This sequence consists of the root functions of the adjoint boundary value problem, and these also form the Riesz basis (see [16]). The adjoint problem to the boundary value problem (5) – (7) is as follows:

— Y ‘‘ (x) + q(x)Y (x) = XY (x),

Y ‘ (0) — Y (1) = 0,

Y ‘ (1) — Y (1) = 0.

It is clear that the boundary value problem (5) – (7) is not self-adjoint. The eigenfunctions of the boundary value problem (10) – (12) are

Y _k,1 (x) = 2kn cos2knx + sin2knx + O

(a

Yk, 2 (x) = (2k + 1)n cos(2k + 1)nx — sin(2k + 1)nx + O

(a

2.    Uniqueness of the Solution

If A = ^ k (ReM k >  0) is written in the equations (8), (9),

Q k (i ) = {

ake-µ2kξ, bk cos Mki + Ck sin Mki,

i> 0, i< 0,

is obtained where a _k ,b _k and c _k are arbitrary constants. Since it is V(x,i) Е ш , it is also V _k (x,i ) = Z _k (x)Q _k (i ) for the solution V _k (x,i ) Е ш. Let us choose the constants a _k ,b _k ,c _k such that

^Q k ⁽⁰⁺⁾ = ^Q k ^{(0 - )}, Q k ⁽⁰⁺⁾ = Q k ^{(0 - )}

conditions are satisfied. The function (13) satisfies condition (14) if and only if a _k = b _k and c _k = -M k a _k . Then the function (13) is

Q k (i) = {

bke-µ2kξ, bk cos Mki - Mkbk sin Mki,

i> 0, i< 0.

Consider the following function, where V(x, i) is the solution of the boundary value problem (1) – (4):

V k (i) = / V(x,i)Y k (x)dx.

If the function (16) is differentiated once when i >  0 and twice when i < 0, the following equations are obtained from the conditions (3), (4) and (11), (12):

^V k ⁽ⁱ) = di (/ ^V(x,i)Y k ^(x)dx) = У ^(V xx ^(x,i ) — q^(x)V(x,i)) Y k ^(x)d = -Mk ^ Y k (x)V(x,i )dx =

^{— M}k Vk ⁽ⁱ )•

Then,

Vk(i ) + M k V k (i ) = 0,

i> 0.

Similarly,

V ’ (i) + 4 V k (i) = 0,

i< 0.

Therefore, for A = M_k (ReM k ^ 0), the differential equations (17), (18) and the equations (8), (9) coincide:

V k (i) = Q k (i ),    i Е [-a,e ]•

To find the coefficients b k in expression (15), let us satisfy the initial condition (2):

V k ( - a) = У V(x, -a)Y k (x)dx = J ^(x)Y k (x)dx = ^ k •

From (15) and (19),

b k [cos M k a + M k sin M k a] = ^ k •

From relation (20), when

d(k) = cos M k a + M k sin M k a = 0,

we have b  ^k  ^k cos Mka + Mk sin Mk a   d(k)

Substituting (22) into the (15), we obtain

V k (C) _

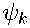
_e - µ ² _k ξ

^ k ddkh) ^, cos M k C - M k sin M k C d(k)

C> 0,

C< 0.

To show the uniqueness of the solution, let us consider ^(x) = 0, i.e. the homogeneous case. Let us also assume that condition (21) is satisfied. Then, according to the formulas (16), (23) and ^(x) = 0, for V C G [-a, в ],

V(x,C)Y _k (x)dx _ 0.

Since the sequence { Y _k (x) } is a Riezs base in the space L 2 (0,1), it is a complete sequence. Then from the last equation we get V(x, C) = 0 almost everywhere for V C G [-a, в ]. Since the function V(x, C) is continuous in the closed region A , V(x, C) = 0 in this region.

Since the system { Y _k (x) } forms a basis in L 2 (0,1), it follows that it is also a complete system i.e. V(x,C) = 0 almost everywhere for any C G [ - a, в]• Since V(x, C) is continuous in the closed A region, it follows that V (x, C) = 0 in A.

Thus, the following uniqueness theorem is proved.

Theorem 1. If there is a solution to the boundary value problem (1) – (4) and the condition (21) is satisfied, this solution is unique.

Suppose that for a number a and k _ p, condition (21) is not satisfied, i.e.

d(p) _ cos M _P a + m _p sin M _p a _ 0.

Then the following non-zero solution of the homogeneous boundary value problem (1) – (4) for ^(x) = 0 is found:

^V P ^(x,C) ^_ I

bpe     Zp(x), bp (cos MpC — Mp sin MpC) Zp(x),

C> 0,

C< 0,

where b p _ 0 is an arbitrary constant. Therefore, if there is a solution to the boundary value problem (1) – (4), this solution is unique if and only if the condition (21) is satisfied.

3.    Existence of the Solution

Suppose d(k) _ 0, and there is such a constant c ₀ that the inequality | d(k) | >  c ₀ > 0 is satisfied. The solution of the boundary value problem (1) – (4) can be represented as a=b.

∞

V(x,C)_ £V k (C)Z k (x).                           (25)

k=1

It is clear that the function V k (£)Z _k (x) satisfies the equation (1). In order to show the existence of a solution to the boundary value problem (1) – (4), it is necessary to show that this series is uniformly convergent in the closed region A , differentiable once with respect to £ when £ < 0, twice with respect to t when £ > 0 and differentiable term by term with respect to x. For this, let us obtain evaluations for functions V k (£).

Lemma 1. For all k E Z ₊ the following inequalities are true for £ E [—а, в ],

| V k (£) | <  A i k [Ф к | ,    | V k ‘ (£) | <  A 2 к ² Ик | ,                         (26)

and for £ E [—а, 0],

| V k ‘‘ (£) |< А з к ³ | Ф к | .                                      (27)

Proof. From (23) for £ E [0, в ] we obtain

| V k (£ ) | =

_e - µ ² _k ξ

^{Ф к} dk

< — <  A + k !Ф к | ,

C o

К (£ ) | =

-^ 2 ^ф к

_e - µ ² _k ξ d(k)

< ^ Ф |< A + k ² |Ф к | . c _o

Similarly, for £ E [ — а, 0] we obtain

| V k (£ ) | =

К(£ ) | =

ψ

d(k)

| V"(£ ) | =

ψ k

cos Ц к £ — Ц к sin ц_к£ d(k)

Ц к (sin Ц_кІ + Ц_k cos Ц_кІ)

^ф к „2 d(k) ^{Ц к}

^Ф J 1 + м 2 <  A - k |ф к | , c o

< — ^| Ц k | J ¹ + Ц 2 <  A 2 k ^{2 |} Ф k | , c o

(cos ц _k£ — Ц к sin Ц_к£ )

= |Ц k | ² |V k (£) | <  A 3 k ³ | Ф к | •

Here, A ± (j = 1, 2, 3) are positive constants. Find the evaluations (26) and (27) from the inequalities shown above.

□

Applying Lemma 1, the series (25) can be bounded from above by the following numerical series with the first-order derivative in the closed domain A and the second-order derivative in the appropriate domains A ₊ and A - according to evaluations (26), (27):

∞

A 4 £ k ³ |Ф k | •                                    (28)

к=1

Now let us obtain evaluations for ψ .

Lemma 2. If ф(х) E C4 [0,1] andф(1+і)(1)+ф(і)(0)—ф(і)(1) = 0, ф(1+і) (0) = 0, i = 0, 2, then, фк =       ' , k e Z+,                              (29)

|µ | where

∞

E|  < IkMhw k=1

Proof. Consider the integral (19):

V k (—a) = У V(x, —a)Y k (x)dx = J -(x)Y k (x)dx = - k .

According to the (10), we have

- k = I -(x)Y k (x)dx =        [ -(x) [-Y’(x) + q(x)Y k (x)) dx =

J o                     Wk ^{| 2} Jo

1     Г1                          1 f1

= —;—~ I -(x)Y k (x)dx + I—г? I -(x)q(x)Y k (x)dx. Wk ^{| 2} Jo                      Wk ^{| 2} Jo

Integrating the last equation twice, from conditions (2) – (4), we find

- k = -|~|| 2 У - " (x)Y k (x)dx + j ^p У -(x)q(x)Y k (x)dx.

Considering the asymptotic expression of µ k in this equation, we obtain

Hk l< MM Hk ²⁾ I , ^M> 0. k

As a result of comparable operations,

^k ²⁾ = - A f - ⁽⁴⁾ (x)Yk (x)dx + A Г ^"(x)q(x)Yk (x)dx = Wk E Jo                  WkE Jo

=^|+ C i-^i -kk

Therefore,

I^r) I < § ^к“1 , where C, C 1 are positive fixed numbers. Substituting inequality (32) for

(31) yields

inequality (29), in accordance with the conditions of the lemma where ^ ⁽⁴⁾ (x) E C [0,1]. Therefore, based on the theory of Fourier series, the series £ ^ 1 | — k⁴ | is convergent and inequality (30) holds true.

□

Under the conditions of Lemma 2, the series (28) is upper bounded by the numerical series

∞ a E >n

k=1

Then, due to the convergence of the series (33), by Weierstrass criteria the series (25) and its derivatives are absolutely and uniformly convergent in A ₊ and A - regions, respectively.

Therefore, the sum of the series (25) is V(x, £) E w , so the equation (1) is satisfied.

Theorem 2. The solution to the boundary value problem (1) – (4) exists and is unique and is defined by the series (13).

If d _a (p) =0 for a number a and a number k = p = k ₁ ,k ₂ ,...,k m (0 <  k 1 < k ₂ < ... < k m <  k ₀ , k i , (i = 1,m) and m being a fixed natural number), then the necessary and sufficient condition for the boundary value problem (1) – (4) to be solvable is to satisfy the equality

^ k =

У ^(x)Y k (x)dx = 0,

k = k 1 , k 2 , ..., k m .

In this case the solution V(x, £) is defined by the following series:

/ k 1 - 1 k m - 1 M \

V(x-^)= ( E⁺- E + E I V kК )Z k (x) + EAp V p l¹^)• (35) \ k=0 k=k m -i + 1 k = k m ₊ 1l p

In the last term the number p takes the values k 1 , k ₂ ,..., k m . The number A _p is an arbitrary constant and the function V _p (x, £) is expressed by the formula (24) such that if the upper limit is less than the lower limit in the sum symbol on the right-hand side of equation (35), this term is set equal to zero.

Theorem 3. Let q(x) G C [0,1], ^(x) G C ⁴ [0,1], ф ^{( і +1)} (1) — ф ^{( і )} (1) + ф ^{( і )} (0) = 0 and ф ^{( і +1)} (0) = 0. Then, for every k = 0, k ₀ , if d _a (k) = 0, the boundary value problem (1) — (4) has only one solution, which is determined by the series (13). If d _a (k) = 0 for any k = k ₁ ,k ₂ ,...,k _m <  k ₀ , then the boundary value problem (1) — (4) has a solution if and only if condition (34) is satisfied, and this solution is defined by the series (35) and V (x,<) G C 1 ( A ) П C ² ( A - ) П C X (A + ).

4.    Stability of the Solution

Theorem 4. Suppose that the conditions of Theorem 3 are satisfied and d _a (k) = 0, k = 0,k ₀ . Then the inequality

\\V (x,< ) \ c ( A ) <  A IH‘(x)ll c[0,1]

is true for (13) solutions of the boundary value problem (1) – (4), where the constant A >  0 does not depend on ^(x).

Proof. Let (x, £) G A be an arbitrary point. In the interval [0,1], | Z _k (x) | <  M 1 >  0. From the inequalities (26) and (31), according to the Cauchy–Schwarz inequality, we have

∞∞

| V(x.€) | < EI V kК ) l| Z k (x) l <  M Т^Фк I <  k=1                       k=1

< M2 £     M2 (E A k=1                  k=1

11 ∞ E k k=1

}  < M 3 H"( x )llL 2 (0,1)

where M j , j = 1, 2, 3 are positive constants. ^