Some estimates for the generalized Fourier transform associated with the Cherednik-Opdam operator on r

In [1], Abilov et al. proved two useful estimates for the Fourier transform in the space of square integrable functions on certain classes of functions characterized by the generalized continuity modulus, using a translation operator.

In this paper, we prove some estimates in certain classes of functions characterized by a generalized continuity modulus and connected with the generalized Fourier transform associated to T^(а,в) in L^(R) analogs of the statements proved in [1, 2-4]. For this purpose, we use a generalized translation operator.

In section 2, we give some definitions and preliminaries concerning the generalized Fourier transform. Some estimates are proved in section 3.

2.    Preliminaries

In this section, we develop some results from harmonic analysis related to the differentialdifference operator T^(а’^в). Further details can be found in [5] and [6]. In the following we fix parameters а. в subject to the constraints a ^ в ^ — 2 ^{ai 1(}-1 a >  — ^.

Let p = а + в + 1 ^{ai 1(}-1 X € C- The Opdam hyper geometric functions G^’^) о n R are eigenfunctions T^(а,в) G^’^) (x) = iXG^’³') (x) of the differential-difference operator

T ^{(a ,в)} f (x) = f ‘(x) + [(2a + 1) coth x + (2в + 1) tanh x] ^x —^^—— — pf (—x)

that are normalized such that G^’^) (0) = 1. In the notation of Cherednik one would write T^(a ,£)

T(ki + k2)f(x) = f‘(x) + { 1 +k-2x + 1—-k-x } (f(x) — f(—x)) — (k1 + 2k2)f(x), with a = ki + k2 — 2 aiid в = k2 - 2- Here ki is the multiplicity of a simple positive root and k2 the (possibly vanishing) multiplicity of a multiple of this root. By [5] or [6], the eigenfunction (a ’в)

GX is given by

GA^Cx) = Fx^ (x) — —17V       (x) = Fx9 (x) + ТГ7   sinh(2x>“+1’e+1(x), p — iX ox                    4(a + 1)

where у“’^в(x) =2 F1 (Уу^; УУ; a + 1; — sinh² x) is the classical Jacobi function.

Lemma 2.1 [7]. The following inequalities are valid for Jacobi functions Fx’^e (x)

0) УУ³(x)l s 1;

• (ii)    1 — Fx’^e(x) S x²(X² + p²).

Denote L^e (R) ? the space of measurable functions f оn R such that

IlfIkaF

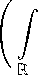
1/2

If (x)|²Aa,e(x) dx 1

< +ro,

Aa,e (x) = (sinh |x|)^2a+1(cosh |x|)^2e+1.

The generalized Fourier transform of f € C_c(R) (the space of continuous functions on R with compact support) is defined by

H f (X) = j f (x)GX^a,e)(—x)A_a,e(x) dx for all X € C.

R

The inverse transform is given as

H-1g(x) = / g(X)G(a’e) (x) (1 —   )     dX x X     iX/ 8n|Ca,e(X)I2

R here

,             2^р-1ХГ(а + 1)r(iX)

ca’e(X) = Г(2(p + iX))r(2(a — в + 1 + iX))'

The corresponding Plancherel formula was established in [5], to the effect that where f (x) := f (—x) and da is the measure given by

^A      16п | С а,в (A) | ² ‘

According to [6] there exists a family of signed measures pX^ such that the product formula

G^x^ ) (y) = j G^z) d^h),

R holds for all x, y G R arid A 6 C. where k.,(x,y,z)Aa,e(z) dz, xy = °;

and

dh^ ^(z) =

dF. (z), d§y (z),

У = °; x=°

π

К_а,в (x,y,z) = M_a,e I sinh x x sinh y x sinh z | ^2a j g(x,y,z,x) + ^{в 1}

x 1

-

χχχ ρ ax,y,z + ax,z,y + az,y,x + в + 1

coth x x coth y x coth z(sin x)² (sinх)^2в dx,

if x, y, z G R \{ ° } satisfy the triangular inequality || x — y || <  | z | <  | x | + | y |, a nd K_a,e (x, y, z) = ° otherwise. Here

^χ σ x,y,z

=

cosh x +cosh y —cosh z cos x sinh x sinh y

°,

xy = °; xy = °

^{(V x,}y^{,z G R}, x ^G [°,^1])

and

g(x, y, z, x) = 1 - cosh² x — cosh² y x cosh² z + 2 cosh x x cosh y x cosh z x cos x-

Lemma 2.2 [6]. For all x,y G R, we have

• (i)    к а,в (x,y,z) = к а,в (y,x,z);

• (ii)    K a,e (x,y,z) = K a,e ( — x,z,y);

• (iii)    K a,e( x,y,z ) = K a,e(— z,y, - x).

The product formula is used to obtain explicit estimates for the generalized translation operators

т^{(а,в) f (}y) = j ^{f (}z) d^ Xay ^e)(z⁾.

R

It is known from [6] that

H T < ^a,e)f (A) = G l ^a,e)(x)H f (A),

for f G C c(R ).

For а > — 2- we introduce the Bessel norm;dizcd function of the first hind j_a defined by

^  (-nnZ x r2n ja(x)=г(а + 1)^2      -I-—, x G R

^^ nil (n + а + 1)

n =0

In the terms of ja (x). we have (see [8])

VhxJ_a(hx) = O(1), hx ^ 0,                              (2)

where Ja(x) is Bessel function of the fir st hind, which is related to ja(x) by the formula.

2 ^a Г(a + 1) j a^(x) = ----— ----^J a^(x) -

Lemma 2.3 [9]. Let а ^ в ^ y^¹, а = -21. Then for | v | ^ p, there exists a positive constant co such that

1^{1 —} T^iv ^(x)| >  co | 1 ^{— j}a^(Ax)| .

For f G La в (R) ^we define the finite differences of first and higher order as follows:

A h f = A h f = (^^ + t^ — 2I ) f,

Ahf = Ah(Ah-1f) = ,      + t^ — 2I )k f, k = 2,3,..., where I is the unit operator in the space Lae(R)-

The generalized modulus of continuity of a function f G La p (R) is defined by

6 > 0.

^ ^(f,6) 2 , a , p = SUp ||^Ah^f || 0 ^a ’^p

3.    Main Result

The goal of this work is to prove some estimates for the integral

J N (f )= / ( H f (A) |² + H f«) d»(A),

N in certain classes of functions in La p(R).

Lemma 3.1. If f G C _c (R). then

H T x^a ’ ^p) f (A) = G^ ’ ^p) ( — x)Hf(A).                             (4)

< F< >r f G C_c (R ). we have

H Tx^a ’ ^p)f (A) = j Tx^a ’ ^p)f (—y^G^^ ’ ^в)(—y)Aa , p (y) dy = j Tx^a ’ ^p)f (y^G^^ ’ ^e)(y)Aa , p (y) dy RR

= y jf (z)Ka,p (x,y,z)Aa,p (z) dz G\

'l^a’^p)( y ^)Aa,p ⁽ y ⁾ dy

RR

= / f (z) /

RR

G^d³" ) (y)Ka,p (x, y, z)A a,p (y) dy Aa,p (z) dz.

Since Ka,e(x,y,z) = Ka,e( - x,z,y) if follows from the product formula that

H тХ^авЧ (A) = G^-x) У f (^(z^ (z) dz

R

= G^)( - x) У f (-z)G^a'^e(-z)Aa,e(z) dz = Gl^a,e)( - x)Hf(A). ▻

R

Lemma 3.2. For f G Lae ( R )’ then

+^

\\Ahf \ 2,a,e = 2^2k У K’^e (h) - 11 2k (H/(A) | ² + | Hf(A) | ²) da(A).

• <1 From formulas (1) and (4), we have

H(Af)(A) = (g^ (h) + G^H-h) - 2)^kH(/)(A)

H(A h f)(A) = (G < ^a,e)(-h)+ G^(h) - 2) k H(f)(A).

Since

G( a ^,e)(h)=^^,e(h) +    ^p    sinh(2h)^ a ^+1,e+1 w,

(a' + )

and ^ iy oven. then

H (A h f )(A) = 2k (_v a ^,e(h) - 1) k H(f )(A)

H(A h f) (A) = 2k (^ a, ⁸(h) - 1) k H(f)(A). ▻

Now by Plancherel Theorem, we have the result.

Theorem 3.1. Given k and f G Lae ( R )• Then there exist a constant c >  0 such that, for all N >  0.

J N (f ) = OMf,CN ^-1)2 ,a в )■

• < Firstly, we have

+^            +^

J N (f) <  У | j a (Ah) | d^(A)+ У | 1 - j a (Ah) | d^(A),

N

N

with d^(A) = (|H f (A)|² + |H f (A)|²)da(A). The parameter h >  0 will be chosen in an instant. In view of formulas (2) and (3), there exist a constant c 1 > 0 such that

| ja(Ah) | ^ C1(Ah)^-a-2 .

Then

+^

У | j a (Ah) | d^(A) ^ C 1 (hN)^-a-2 J N (f).

N

Choose a constant c ₂ such that the number C3 = 1 — c 1 c-“ ² is positive.

Setting h = C 2 /N in the inequality (5), we have

+∞

C 3 JN(f) < У |1 - ja(Ah)| d^(A).

N

By Holder inequality and Lemma 2.3 the second term in (6) satisfies

+∞               +∞ j |1 — ja(Ah)| d^(A) = j |1 — ja(Ah)| X 1 d^(A)

N

N

+∞

N

1 / 2 k

— ja(Ah)|2k d^(A)

1-1 / 2 k

< I J ^{11 —}

N

N ja(Ah)|2k d^(A)^     (Jn(f))2-1/к

<          11 — c0 N

^ (h)|^2k W)}    ( Jn (f ))^2-1/к

.

From Lemma 3.2, we conclude that

+∞ j |i—.(

N

Therefore

N

For h = c₂/N. we obtain

— ja(Ah)|d^(A) ^ ^|Ahf^2/a^ke(Jn(f))^2-1/k. _c0,,

C3JNN(f) ^ -4f,^2)1^/k (JN(f))^2-1/k. c N 2 α β

Consequently by raising both sides to the power k and simplifying by (Jn(f))^2k we finally obtain

^JN(f ) < f for all N > 0. The theorem is proved with c = C2. >

Theorem 3.3. Let f E L _e(R)• ^Then- ^{for a11} N > 0,

N

^f, N-1)2,a,e = O I N^-2k E(l + 1)4^k-1Ji l=0

<1 From Lemma 3.2, we have

+∞

WС,а,в = 22^k / K^,e(h) - 1Г (|Hf« + |HfW) d^(^A).

This integral is divided into two

+∞  N +∞

/ -/+/

N

^— Ii ⁺ I2,

where N — [h 1]. We estimate them separately.

From (i) of Lemma 2.1, we have the estimate

I2 < c4

+∞

У (|Hf(A)|² + |Hf(A)|²) da(A)

N

— C4JN (f).

Now, we estimate Ii. From formula (ii) of Lemma 2.1, we have

N

Ii ^ h^4k I (A + p)⁴ (|H f (A) |² + |H f (A)|²) da(A) 0

— h^4k

N -1 ^l+1

E / (A + p)^4k (|Hf (A)|² + |Hf(A)|²) da(A^ l=0 _l

< h^4kY,(i+p+1)^4k (Ji²(f) - J+(f)) ■ l=0

From the inequality l + p + 1 < (p + 1)(l + 1) we conclude

-1

Ii ^ (p + 1)^4kh^4k £ ai (J2(f) - j+(f))

l=0

with ai — (l + 1)^4k.

For all integers m > 1, the Abel transformation shows

mm

^al (Ji2^(f) ^— Jl+i^(f)) ^— a0J0^(f) ⁺^^(al^— al-i) Jl^2(f) ^— amJm+i^(f)

l=0                                           l=1

m

< aoJo(f) + ^2 (ai - ai-i) Ji2(f), l=1

because amJm₊i^(f) > °-

Hence

Ii ^ (p + 1)^4kN^-4k

N-1

J02(f) + E l=1

((l + 1)4k

- i*^k)j?(f >),

since N ^ 1/h. Moreover by the finite incremenfs theorem, we have (l + 1)^4k 1)^4k-1. Then

-

l^4k

^ 4k(l +

I1 ^ (p + 1)^4kN-4k

(

N-1

J2(f ) + 4k £(l + 1)

l=1

4k-1

Jf)}.

Combining the estimates for I1 and I₂ gives

Il4f h2ae = O

N

N-4k l=0

(l + 1)^4k-1

Jl²(f)},

which implies

N

^(f,N-1)2ав = O

I N^-2k ^(l + 1)^4k-1J2 l=0

and this ends the proof. >