Some vector valued multiplier difference sequence spaces defined by a sequence of Orlicz functions

Throughout the paper w, ' ^ , c and c o denote the spaces of all bounded, convergent, and null sequences x = (x _k ) with complex terms, respectively. The zero sequence is denoted by θ = (0, 0, 0, . . . ).

The notion of difference sequence spaces was introduced by Kizmaz [11] who studied the difference sequence spaces ' ^ (A), c(A) and c o (A). The notion was further generalized by Et and Colak [4] by introducing the spaces ' ^ (A s ), c(A ^s ) and c o (A ^s ). Recently Dutta [2] introduced and studied the following difference sequence spaces:

Let r, s be non-negative integers, then for Z a given sequence space we have

Z^(A s _r ) ) = n x = (x k ) ^G w : ^(A s _r ) x k ) ^G Z 0

where A sr) X = (A sr ) X k ) = (A S — X k - A S ^-1 X k - r ) and A^x k = X k for all k G N and which is equivalent to the binomial representation A sr ) X k = ^2V =o ( — 1) v(V) X k - rv •

For s = 1, we get the difference operator A ( _r ) introduced and studied by Dutta [3] for sequences of fuzzy numbers. Again r = s = 1, we get spaces ' ^ (A), c(A) and c o (A).

Let Λ = ( λ k ) be a sequence of non-zero scalars. Then for a sequence space E the multiplier sequence space E (Λ), associated with the multiplier sequence Λ is defined as

E (Л) = { (x k ) G w : (X k X k ) G E } .

The scope for the studies on sequence spaces was extended by using the notion of associated multiplier sequences. Goes and Goes [8] defined the differentiated sequence space dE and integrated sequence space E for a given sequence space E , using the multiplier sequences

(c) 2011 Dutta H.

(k ^-1 ) and (k) respectively. A multiplier sequence can be used to accelerate the convergence of the sequences in some spaces. In some sense, it can be viewed as a catalyst, which is used to accelerate the process of chemical reaction. Sometimes the associated multiplier sequence delays the rate of convergence of a sequence.

The concept of 2-normed spaces was initially developed by G¨ahler [6] in the mid of 1960’s. Since then, Gunawan and Mashadi [10], Dutta [1] and many others have studied this concept and obtained various results.

Let X be a real linear space of dimension greater than one and let k· , ·k be a real valued function on X × X satisfying the following conditions:

• (1)    k x, y k = 0 if and only if x and y are linearly dependent vectors,

• (2)    k x, y k = k y, x k ,

• (3)    k αx, y k 6 | α | · k x, y k , for every α ∈ R

• (4)    k x,y+z k 6 k x, y k + k x, z k

then the function k· , ·k is called a 2-norm on X and the pair (X, k· , ·k ) is called a 2-normed linear space.

An Orlicz function is a function M : [0, ∞ ) → [0, ∞ ) which is continuous, non-decreasing and convex with M (0) = 0, M (x) > 0 , for x > 0 and M (x) → ∞ , as x → ∞ .

Lindenstrauss and Tzafriri [14] used the Orlicz function and introduced the sequence space ` M as follows:

∞

' m = j (xk) € w : X M k =1

| x k | ^ρ

< ∞ , for some ρ > 0 .

They proved that ` M is a Banach space normed by

k (x k ) k = inf

{P> 0^ M (V) 6 1}.

Remark 1. An Orlicz function satisfies the inequality M (λx) < λM (x), for all λ with 0 < λ < 1. The following inequality will be used throughout the article.

Let p = (p k ) be a positive sequence of real numbers with 0 < p k 6 sup p k = G, D = max ( 1, 2 G ¹ ) . Then for all a k , b k € C for all k € N , we have

|ak + bk|pk 6 D {|ak|pk +|bk|pk} and for all A € C, |A|pk 6 max (1, |A|G).

The studies on paranormed sequence spaces were initiated by Nakano [17] and Simons [20] at the initial stage. Later on it was further studied by Maddox [15], Nanda [18], Las-cardies [12], Lascardies and Maddox [13] and many others. Parasar and Choudhary [19], Mursaleen, Khan and Qamaruddin [16] and many others studied paranormed sequence spaces using Orlicz functions.

• 2.    Definition and Preliminaries

A sequence space E is said to be: solid (or normal) if (x _k ) ∈ E implies (α _k x _k ) ∈ E for all sequences of scalars (α k ) with | α k | 6 1 for all k ∈ N ; monotone if it contains the canonical preimages of all its step spaces; symmetric if (x _n ( k ) ) € E whenever (x k ) € E , where n is a permutation on N ; convergence free if (y k ) ∈ E whenever (x k ) ∈ E and y k = 0 whenever x _k = 0; sequence algebra if (x _k , y _k ) ∈ E whenever (x _k ) ∈ E and (y _k ) ∈ E.

A sequence (x _k ) in a 2-normed space (X, k· , ·k ) is said to converge to some L ∈ X in the 2-norm if lim k_→∞ k x k - L, u k = 0, for every u ∈ X , and is said to be Cauchy sequence with respect to the 2-norm if lim _{k,l →∞} k x _k - x _l , u k = 0, for every u ∈ X .

If every Cauchy sequence in X converges to some L ∈ X, then X is said to be complete with respect to the 2-norm. Any complete 2-normed space is said to be 2-Banach space.

Now we give the following two familiar examples of 2-norm which will be used in the next section to construct examples.

Example 1. Consider the spaces ' ^ , c and c g of real sequences. Let us define:

kx, yk = sup sup |xiyj - xjyi|, i∈N j∈N where x = (xi, x2, X3,...) and y — (yi, y2, Уз,...). Then Ц’, •k is a 2-norm on '^, c and cg.

Example 2. Let us take X = R ² and Consider the function Ц’ , -| on X definded as:

k x i , X 2 | e = abs

x ii x i2

^x 2i ^x 22

x i — ^(x i 1 ^,x i 2 ) ^{e R} , i — 1, ²*

Then k· , ·k is a 2-norm on X.

Let p = (p k ) be any bounded sequence of positive real numbers and Λ = (λ k ) be a sequence of non-zero reals. Let m, n be non-negative integers, then for a real linear 2-normed space (X, k· , ·k ) and for a sequence M = (M k ) of Orlicz functions we define the following sequence spaces:

c g ⁽M, lh •k, A m ) ,^Л,Р) = x = (x k ) ^e w^(X) :

lim k →∞

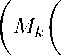
A m ) ^X k X k ^ρ

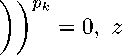
∈ X, for some ρ > 0 ,

c(M, |. , •k , А Пт ) , Л,р)

x = (x k ) ∈ w(X) :

lim k →∞

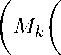
∆ ⁿ λ x - L

( m ) ^{k k}

,z ρ

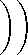
= 0, z ∈ X, L ∈ X, for some ρ > 0 ,

'^^(M, II¹ , •k , ^А Пт ) , ^Л,Р) = 1 ^x = ^(x k ) ^{e w(X}) ^:

sup k>1

^An X k x k

,z ρ

p k

< ∞, z ∈ X, for some ρ > 0 , where (A^m)Xkxk) — (A^Xkxk - A^Xk-mxk-m) and Agm)Akxk — Xkxk for all k e N and which is equivalent to the binomial representation

n

λ k - mv x k - mv ^.

A’rnX- xk = Е<-^’ v=g

In the above expansion it is important to note that we take x k _{- mv} = 0 and λ k _{- mv} = 0, for non-positive values of k - mv.

It is obvious that cg(M, |., •k, A(m), Л,р) C c(M, k-, •k, A(m), Л,р) C '_(M, k^, •k, A(^), Л,р).

The inclusions are strict as follows from the following examples.

Example 3. Let m = 2, n = 2, M k (x) = x ² for all k is odd and M k (x) = x ⁶ for all k is even, for all x ∈ [0 , ∞ ) and p _k = 1 for all k > 1. Consider the 2-normed space as defined in Example 2 and let the sequences Л = (k ⁴ ) and x = (^ 2 , ^ 2) . Then x G c(M, Ц’ , •k , ^A 2 ₂ ) , Л,р), but x / c ₀ ^(M , ||- , •k , A 22) , ^л,р).

Example 4. Let m = 2, n = 2, M k (x) = | x | , for all k > 1 and x ∈ [0, ∞ ) and p k = 2 for all k odd and p _k = 3 for all k even. Consider the 2-normed space as defined in Example 1 and let the sequences Λ = (1, 1, 1, . . . ) and x = { 1, 3, 2, 4, 5, 7, 6, 8, 9, 11, 10, 12, . . . } . Then x ^G ' _x (M, ||- , •k , ^A 22) , ^Л,Р), but x / c⁽M, Ц- , •k , ^A 22) , ^Л,Р)-

Lemma 1. If a sequence space E is solid, then E is monotone.

• 3.    Main Results

In this section we prove the main results of this article.

Proposition 1. The classes of sequences ^c o ^(M, ||-, -||, ^A nm ) , ^л,р), ^c(M ||-, -||, ^A nm ) , ^л,р) and ' ^ (M, ||- , - I , A nm ) , Л,р) are linear spaces.

Theorem 2. For Z = '^, c and cg, the spaces Z(M, Ц*, •I, Anm), Л,р) are paranormed sapces, paranormed by pk

g(x) = inf ρ ^H

: sup Mk k>1

^A ( m ) ^X k x k ^ρ

z 6 1, z G X

where H = max(1,sup k >₁ p k ).

C Clearly g(x) = g( - x); x = θ implies g(θ) = 0. Let (x _k ) and (y _k ) be any two sequences of the space c g (M, Ц^ , •I , A nm ) , Л,р). Then there exist p _i , p ₂ > 0 such that for every z in X,

sup M _k k > i

^A nm ) X k x k

,z pi

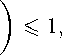
sup M _k k > i

^A nm ) ХУ

P 2

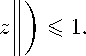
Let p = p i + p 2 . Then by the convexity of Orlicz functions, we have for every z in X

sup M k k

Hence we have,

^A ( m ) ^X k x k ^{+ A} ( m ) ^X k y ^{k ρ}

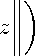
p i

6         sup Mk pi + p2   k

p 2

+        sup Mk pi + p2   k

p _k

g(x + y) = inf ρ ^H : sup M k

k > i

6 inf

p _k

P i ^H

: sup M _k k > i

^A ( m ) ^X k x k P i

p _k

+ inf < p ₂ H : sup M k k > i

^A nm ) ^X k y ^k P 2

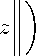
^A ( m ) ^X k x k ^{+ A} ( m ) ^X k y k

,z ρ

^A ( m ) ^X k x k

,z pi

^A nm ) ^X k y k

P 2

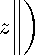
6 1, z ∈ X

6 1, z ∈ X

6 1, z ∈ X = ⇒ g(x + y) 6 g(x) + g(y).

The continuity of the scalar multiplication follows from the following equality:

g(αx) = inf

p _k

ρ H : sup Mk k>1

= inf (t | α | ) ^Hk : sup M k

I             k > 1

^A ( m ) ^aX k x k

,z ρ

A(m)Xk xk t ,z )

6 1, z G X

6 1, z G X

where t = Д Hence the spaces c _o (M, ||- , •k , A^ m ) , Л,р) is a paranormed space, paranormed by g. The rest of the cases will follow similarly. B

Theorem 3. If (X, ||-, •k) is a 2-Banach space, then the spaces Z(M, ||-, •k, A^m), Л,р), for Z = '^, c and co are complete paranormed spaces, paranormed by pk

g(x) = inf ρ ^H : sup M k k > 1

^A ( m ) ^X k x k

,z ρ

6 1, z G X

where H = max(1,sup k > 1 p k ).

<1 We prove the result for the space ' ^ (M, ||- , •k , A^ m ) , Л,р) and for other spaces it will follow on applying similar arguments.

Let (xi) be any Cauchy sequence in '^(M, ||-, •k, A^m), Л,р). Let xo > 0 be fixed and t > 0 be such that for 0 < e < 1,    > 0 and xot > 0. Then there exists a positive integer x0t no such that g(xi — xj) < -Ц, for all i, j > no. Using the definition of paranorm, we get x0t inf

p _k

ρ H : sup Mk k>1

^A ( m ^X k ^(x k ^— x k ) ^ρ

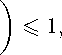
z ∈ X

ε

< xot

( V i, j >  n o ).

Then we get for every z in X

sup M k k > 1

^A" m) ^X k ⁽ x k - x k ) g(x ⁱ - x ^j )

( V i,j >  n o ).

It follows that for every z G X and k >  1

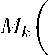
^A" m) ^X k ⁽ x k - x k ) g(x ⁱ - x ^j )

( V i,j >  n o ).

Now for t >  0 with M k ( tX j ⁰ ) > 1, for each k >  1

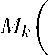
^AX m) ^X k ⁽ x k - x k ) g(x ⁱ - x ^j )

6 M k

txo \

2,

z ∈ X.

This implies that

|| A (- m ) X _t x k — A? m , X k x , z || 6 ('x")     ) = f. z G X.

2 tx o 2

Hence (A^ m ) X k xk) is a Cauchy sequence in 2-Banach space X for all k G N . ^ (A^ m ) X k xk) is convergent in X for all k G N . For simplicity, let lim i ,^ A^T ( _m ) X k x k = y k for each k G N . Let k = 1, we have

n lim Anm)Aix! = lim X(-1)v(  )Ai—mvxi-m,

= lim A i x l = y 1 . i →∞

i→∞          i→∞ v=0

Similarly we have lim Anm)Ak xk = yk, k = 1, 2,...,nm.(2)

i →∞

Thus from (1) and (2) we have lim i ,^ x\ _{+ nm} exists. Let lim i ,^ x 1+n _m = x _1+nm . Proceeding in this way inductively, we have lim i_→∞ x ⁱ _k = x k exists for each k ∈ N . Now we have for all

i, j >  n o .

pk inf ρ H : sup Mk

I        k > i

^A ( m ) ^A k ^(x k ^— x k )

,z ρ

6 1, z ∈ X 6 ε

p _k

=⇒ lim inf ρ H : sup Mk j 'x       I         k>1

A m A - A m ^A k . z ρ^,

6 1, z ∈ X 6 ε

p _k

=⇒ lim inf ρ H : sup Mk j^^ I     k>1

^A(m ) ^A k X k

-

ρ

^A ( m ) ^{A k} x ^k

,z

6 1, z E X >  6 e ( V i >  n _o ).

It follows that (x i - x) E ' ^ (M, Ц- , •k , A nm ) , Л,р).

Since (x i ) E ' ^ (M, Ц- , •k , A nm ) , Л,р) and ' ^ (M, Ц- , •k , A nm ) , Л,р) is a linear space, so we have x = x i — (x i — x) E ' ^ (M, ||- , •k , A nm , Л,р . This completes the proof. B

Theorem 4. If 0 < P k 6 q k <  to for each k, then Z ( M, Ц- , •k , A nm , Л,р ) C ^Z ( ^M, lh -lb A m) , ^q ) , ^{for Z} = c o and c.

C We prove the result for the case Z = c o and for the other case it will follow on applying similar arguments.

Let (xk) E co(M, ||-, •k, Anm), Л,р). Then there exist some p > 0 such that get

This implies that

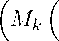
^ nm ) ^ ^k x k ^ρ

lim k →∞

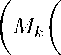
lim k →∞

A m) ^A k x k

,z ρ

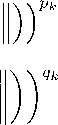
^A nm ) ^A k x k

,z ρ

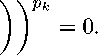
< ε (0 < ε 6 1) for sufficiently large k. Hence we

6 lim k →∞

A m) ^A k x k ^ρ

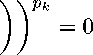
= ^ (x k ) E c o (m, k^ , •k , A nm) , Л,q).

Thus c o (M, !• , •k , A nm ) , Л, p) C c o (k M, • , •k , A nm ) , Л, q).

Similarly, c ( M, Ц- , •k , A nm ) , Л,р ) C c ( |M, • , •k , A nm ) , Л,q ) . This completes the proof. B

The following result is a consequence of Theorem 6.

Corollary 5. (a) If 0 < inf p _k 6 p _k 6 1 , for each k , then

Z(M, k^ , •k , A nm) , Л,р) C Z(M, k^ , •k , A nm) , Л), Z = c o ,c.

(b) If 1 6 p _k 6 sup p _k <  ∞ , for each k , then

Z ( M, k^ , •k , A nm) , Л ) C Z ( M, k^ , •k , A nm) , л,р ) , Z = c o ,c.

Theorem 6. Z(M, Ц- , •k , A n— , Л,р) C Z(M, Ц- , ’k , A nm , Л,р) (in general for i = 1, 2,...,n - 1) Z (M, k’ , •k , A— , Л,р) C Z (M, k’ , •k , A nm , Л,р)), for Z = ' ^ , c and c g .

C Here we prove the result for Z = c g and for the other cases it will follow on applying similar arguments.

Let x = (xk) E cg (M, ||’, -k, An—, Л,р). Then there exist p > 0 such that lim k→∞

— m—k^k ^ρ

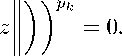
On considering 2ρ, by the convexity of Orlicz functions, we have

^A ( m ) ^X k x k 2ρ

^A nm) ^ ^k x k ^ρ

1 +2

ρ

"A,

( _m ) k - m x k - m

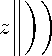
Hence we have

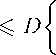
^ nm^ X k x k ^ρ

Then using (3), we get

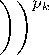
^А Пт ) X k X k 2 ρ

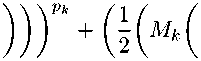
lim k →∞

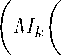
^A ( m ) ^X k x k

2 ρ      ^{, z}

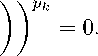
"A,

( _m ) k - m x k - m

ρ

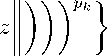
Thus C g (M, k’ , •k , A nm ) ¹ , Л, p) C c g (M, k’ , ’k , A nm , Л— . B

The inclusion is strict as follows from the following example.

Example 5. Let m = 3, n = 2, M k (x) = x ¹⁰ , for all k >  1 and x E [0, to ) and p k = 2 for all k odd and p k = 3 for all k even. Consider the 2-normed space as defined in Example 2 and let the sequences Л = (— and x = (x k ) = (k ² , k ² ). Then A 23) X k x k = 0, for all k E N . Then x E c g (M, k’ , ’k , A 23) , Л,р). Again we have A^ ) X k x k = — 3, for all k E N . Hence x E c g (M, k’ , •k , A 13) , Л,р). Thus the inclusion is strict.

Theorem 7. The following spaces c g ( M, k’ , ’k , A nm ) , M- c ( M, |h ’k , ^A, ^л, p ) and ' ^ Mi k k’ , ’k , A nm ) , Л,р) are not monotone and as such are not solid in general.

C The proof follows from the following example. B

Example 6. Let n = 2, m = 3, p _k = 1 for all k odd and p _k = 2 for all k even and M k (x) = x ² , for all k >  1 and for all x E [0, to ). consider the 2-normed space as defined in Example 1. Then A 23) X k x k = X k x k — 2X k - 3 x k - 3 + X k ₆ x k 6 - for all k E N . Consider the J ^th step space of a sequence space E defined as, for (x k ), (y k ) ∈ E ^J implies that y k = x k for k odd and y k = 0 for k even. Consider the sequences Л = (k ³ ) and x = (—). Then x E Z(M, k’ , ’k , A 23) , Л,р) for Z = ' ^ , c and c o , but its J ^th canonical pre-image does not belong to Z (k M, • , ’k , A 23) , Л,р) for Z = ' ^ , c and c o . Hence the spaces Z(M, k’ , ’k , A nm ) , Л,р) for Z = ' ^ , c and c o are not monotone and as such are not solid in general.

Theorem 8. The following spaces are not symmetric in general: c g (M, k’ , ’k , A nm ) , Л,р) , c ( M, k’ , ’k , A nm ) , Л,р ) , ' ^ ( M, k’ , ’k , A nm ) , Л,р ) .

C The proof follows from the following example. B

Example 7. Let n = 2, m = 2, pk = 2 for all k odd and pk = 3 for all k even and Mk(x) = x2, for all x ∈ [0, ∞) and for all k > 1. Consider the 2-normed space as defined in Example 1. Then ∆(22)λkxk = λkxk - 2λk-2xk-2 + λk-4xk-4, for all k ∈ N.

Consider the sequences Λ = (1, 1, 1, . . .) and x = (x _k ) defined as x _k = k for k odd and X k = 0 for k even. Then A^ X k X k = 0, for all k E N . Hence (x k ) E Z ( M, ||- , •k , Д 22) , Л,р ) , for Z = ` <sub>∞</sub> , c and c <sub>o</sub> . Consider the rearranged sequence, ( y <sub>k</sub> ) of ( x <sub>k</sub> ) defined as ( y <sub>k</sub> ) = ( x 1 ,x 3 ,x 2 ,x 4 ,x 5 ,x 7 ,x 6 ,x 8 ,x 9 ,x 11 ,x 10 ,x 12 , . . . ). Then ( y k ) ∈ / Z ( M, k· , ·k , ∆ <sub>(</sub> <sup>2</sup> <sub>2)</sub> , Λ , p ), for Z = ` _∞ , c and c _o . Hence the spaces Z M, k· , ·k , ∆ ₍ ⁿ _{m )} , Λ ,p , for Z = ` _∞ , c and c _o are not symmetric in general.

Theorem 9. The following spaces are not convergence free in general:

c 0 M, k· , ·k , ∆ ₍ ⁿ _{m )} , Λ ,p , c M, k· , ·k , ∆ ₍ ⁿ _{m )} , Λ ,p , ` ∞ M, k· , ·k , ∆ ₍ ⁿ _{m )} , Λ ,p .

C The proof follows from the following example. B

Example 8. Let m = 3, n = 1, p k = 6 for all k and M k ( x ) = x ⁵ , for k is even and M _k ( x ) = | x | , for k is odd, for all x ∈ [0 , ∞ ). Then ∆ ₍ ¹ ₃₎ λ _k x _k = λ _k x _k - λ _{k - 3} x _{k - 3} , for all k ∈ N . Consider the 2-normed space as defined in Example 2. Let Λ = _k ⁵ and consider the sequences ( x k ) and ( y k ) defined as x k = ⁴ ₅ k, ⁴ ₅ k for all k ∈ N and y k = ¹ ₅ k ³ , ¹ ₅ k ³ for all k E N . Then (x k ) E Z(M, Ц- , •k , А Ц3) ,Л,р ) , but (y k ) / Z(M, Ц- , •k , A^,Л,р ) , for Z = ' ^ , c and c _o . Hence the spaces Z M, k· , ·k , ∆ ⁿ _{m )} , Λ ,p , for Z = ` _∞ , c and c _o are not convergence free in general.

Theorem 10. The following spaces are not sequence algebra in general:

c 0 M, k· , ·k , ∆ ⁿ _{m )} , Λ ,p , c M, k· , ·k , ∆ ⁿ _{m )} , Λ ,p , ` ∞ M, k· , ·k , ∆ ⁿ _{m )} , Λ ,p .

C The proof follows from the following example. B

Example 9. Let n = 2, m = 1, p _k = 1 for all k and M _k ( x ) = x ² , for each k ∈ N and x ∈ [0 , ∞ ). Then ∆ ² ₁₎ λ k x k = λ k x k - 2 λ k _- 1 x k _- 1 + λ k _- 2 x k _- 2 , for all k ∈ N . Consider the 2-normed space as defined in Example 2. Consider Λ = _k ¹ ₄ and let x = ( k ⁵ , k ⁵ ) and y = (k ⁶ , k ⁶ ). Then x,y E Z(M, Ц- , •k , A 21) , Л,р ) , Z = ' ^ and c, but x,y / Z(M, Ц- , •k , A 21) , Л,р ) , for Z = c o Hence the spaces c M, k· , ·k , ∆ ⁿ _{m )} , Λ ,p , ` ∞ M, k· , ·k , ∆ ⁿ _{m )} , Λ ,p are not sequence algebra in general.

Example 10. Let n = 2, m = 1, p _k = 3 for all k and M _k ( x ) = x ⁷ , for each k ∈ N and x ∈ [0 , ∞ ). Then ∆ ² ₁₎ λ k x k = λ k x k - 2 λ k _- 1 x k _- 1 + λ k _- 2 x k _- 2 , for all k ∈ N . Consider the 2-normed space as defined in Example 1. Consider Λ = _k ¹ ₆ and let x = ( k ⁷ ) and y = ( k ⁷ ). Then x,y E c o ( M, Ц- , •k , A 21) ,Л,р ) , but x,y / Z(M, Ц- , •k , A 21) ,Л,р ) , for Z = ' ^ , c. Hence the space c 0 M, k· , ·k , ∆ ² ₁₎ , Λ , p is not sequence algebra in general.