Sorted r-Train: an improved dynamic data structure for handling big data

Published Online November 2018 in MECS

A dynamic data structure in the context of this paper is one that can store the data of variable sizes. When we talk about big data one prominent point that is pertinent to address is “How to store this enormous data”. As these data are so huge that it cannot be stored in a single storage device, therefore we need multiple storage devices to store these big data. At the same time, we need to look for the storage techniques that will somehow link these storage devices together in one or the other way so that the process of data storage and retrieval remains uncomplicated and time efficient. The critical issue about big data lies in its intricate and heterogeneous nature. The major portion of big data generated today is largely unstructured. This means that there is no fixed structure attached with the data. Furthermore big data possesses several characteristics which are exponentially expanding with time and are often represented by 10 V’s of big data in recent years. It is very important to understand the effect of each of these characteristics as they are closely linked to each other and sometimes overlaps with each other. If we are able to effectively identify and analyze these varying characteristics of big data, we can come up with system, tools and techniques to handle these huge datasets in an effective manner. The 10 V’s of big data are shown in Fig. 1.

Fig.1. 10 V’s of big data

There are several techniques evolved in recent times for handling such huge datasets. In [1], the author proposed a new type of dynamic data structure known as “r-Train”. The core idea of the “r-Train” data structure is to store the data items in various “coaches” (which are like data items stored in a linked list). Each coach consists of some data items and the address to reach the next coach, forming a ‘train’ like structure.

• A. r-Train Data Structure: A Brief Introduction

The author of [1] proposed a new dynamic “homogeneous data structure r-Train” which is used to store similar type of data. The main advantage of this data structure that was pointed out by ‘R. Biswas’ [1] is its ability to be scalable to any desired amount as and when required. The difference of r-Train from the data structure arrays lies in a way that, in array we cannot leave an empty space for a data in-between the elements already present in the array, but in case of r-Train it is quite possible. A coach of the ‘r-Train’ may consist of one or more empty spaces. The empty space is being represented by a ‘ɛ’ (also known as null element) which is treated as of same data type as the other elements of the coach. The definition given by R-Biswas asserts an r-Train as a “linked list of tagged coaches”. The term tagged coach means that every coach consists of some data elements (including ‘ɛ’) and the information about how many more elements can be stored in it. The various formal terms and definition related to r-Train data structure are given below in brief [1]. However for detailed information about the functioning of “r-Train”, one could see [1, 2, 3, 4, 5].

• 1)    larray

A ‘larray’ is a collection of similar types of elements where one or more elements can be ‘ɛ’ element or null elements. Since ‘ɛ’ is treated as of same data type, therefore the same amount of space (as that for the other elements) will be reserved in the memory for storing “ɛ” elements. The length of the larray may be defined as the number of elements (including ɛ) stored in it [1]. The following are few examples of larray.

• i.    X = < 2,6,7, ɛ,8, ɛ> , the length of ‘larray’ X is 6

• ii.   Y = <12, 5, ɛ, ɛ, ɛ, 7, 100, 8>, the length of

‘larray’ Y is 8

• iii.   Z = < ɛ, ɛ, ɛ, ɛ>, the length of ‘larray’ Z is 4

• iv.   P = <1, 5, 8, 14, 7>, the length of ‘larray’ P is 5

• v.   Q = < 2 >, the length of ‘larray’ Q is 1

• vi.   R = < ɛ >, the length of ‘larray’ R is 1

• vii.    S = < >, S is an empty larray.

If we have a ‘larray’ where all the elements present in it are ‘ɛ’ (null) elements, then that array is known as “null larray”. Here, larrays ‘Z’ and ‘R’ are said to be “null larrays”. It can also be observed that the lengths of larray ‘Z’ and ‘R’ are ‘4’ and ‘1’ respectively. Therefore it can be concluded that “null larrays” are not unique.

• 2)    Coach of an r-Train

A “Coach (C)” of an “r-Train” may be defined as a pair (LA, add) where “LA” is a “nonempty larray” (can include a “null larray” also) and “add” is the address of the next coach of the “r-Train”. However, if the coach “C” is the last or the only coach of the “r-Train” then “add” will contain an invalid address value [1].

3

5

Е

Е

20

£

24

Е

5

ез

Fig.2. An Example of a Coach of an “r-Train”

Fig. 2 shows a coach C with the items of ‘larray’ as < 3, 5, ɛ, ɛ,20, ɛ,24, ɛ, ɛ, e2> where e2 being the address of next coach. Therefore while creating a coach it must be noted that the last block of the coach must be reserved for storing the address of the next coach and no element (ɛ or non- ɛ) can be stored in it [1].

• 3)    Status of the Coach

It is defined as the number of empty spaces (‘ɛ’ elements) in the larray at a given point in time. It is denoted by “s” and has the value in the range between 0 ≤ s ≤ r . a lso the value of “s” is dynamic in nature and will change with every insertion or deletion of the element to or from the ‘larray’. If the “status” of a coach is “0 (zero)” at any point of time, it signifies that the larray of this coach is full and no more elements can be added in this particular coach [1, 2]. If the “status” of the larray is equal to “r”, it means that the larray is a “null larray” with all the elements as ‘ɛ’ and we can store up to a maximum of “r” number of elements in the larray [1].

• 4)    Tagged Coach of an r-Train

If C (LA, add) is a “coach” of an “r-Train” then the “tagged coach (TC)” of the coach C, is given by a pair (C,s), where “C” is the “coach” and “s” is its “status”. The tagged coach consists of the information about how many empty spaces are available in the coach at any given time. For example : If the Coach C (LA, add) is there with its larray ‘LA’ given by < 2, 5, 7, 21, ɛ, ɛ, 3, ɛ > then the tagged coach (TC) with respect to the coach C will be TC = (C, 3). As we have three number of “ɛ” elements present in the larray “LA” [1].

• II.    General Representation of r-Train Data Structure

As mentioned by the author in [1, 2, 3, 4, 5] an “r-Train” is a homogeneous, dynamic data structure which is highly scalable in nature. It makes the best use of both arrays and linked list data structures to come up with a more powerful and efficient way of managing big data (which arrays and linked lists lack in general) [1]. An “r-Train” may be treated as the “linked list of tagged coaches”. The alphabet “r” represents the number of “tagged coaches (TC)” in the “r-Train”. The general representation of an r-Train “T” of length “k” is given below in Fig. 3.

T = < (C 1 , S C1 ), (C 2 , S C2 ), (C 3 , S C3 ), ......., (C k , S ck ) >,

Where C1, C2 ...... Ck are the tagged coaches and

Also note that C 1 , C2 ...... C k consists of the pairs

(LA 1 , add 1 ) , (LA 2 , add 2 ),  (LA 3 , add 3 )....(LA k ,  add k )

respectively.

Where LA1, LA2, LA3 ....... LAk are larrays with “d11, d21, d31 ... dkr” are the data items and “add1, add2, add3 ............. addk” are the addresses of the next coach

(i.e. add 1 holds the address of coach C 2, add 2 holds the address of Coach C 3 and so on. And ‘add k ’ holds an invalid address as it is the last coach of the r-Train) [1].

Coach (Ci, Set)

Coach (Cs, Sea)

Coach (Сз, Sea}

.............

Coach (Ck, Sck)

• Fig.3. An example of an “r-Train” with “k” number of Coaches

Example: A 4-Train of length 3

Let the 4-Train is denoted by ‘T’ and is given by

T = < (C 1 , 2), (C 2 , 1), (C 3 , 1), (C 4 , 0) >

Where C1 = < 1, ɛ, ɛ, add1 >, C2 < 4, 8, ɛ, add2 >, C3 = < 2, 5, ɛ, add3 > and C4 = < 7, 3, 9, Invalid Address >

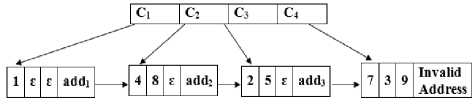
Fig.4. An example of 4-Train of length 3

Fig. 4 shows an example of 4-Train of length 3, similarly, we can create r-Train of any desired length. For further details about r-Train and its implementation, one could see [1].

• III.    Related Work

with big data. In [26], the authors highlighted the need for securing big data and maintaining its authenticity and accuracy for gaining valuable insights from it. The researchers in [27] proposed a model for performing visualization and analytics of big data by transforming the data into structured format and visualizing it through graphs and charts. The authors of [28] proposed a privacy-preserved big data storage technique using “proxy- re-encryption” and anonymity.

• IV.    Sorted r-Train (The proposed Approach)

This paper proposes a modified approach for storing and searching the data in the “r-Train” data structure so that the data becomes sorted and searching can be performed efficiently and effectively. The “r-Train” data structure can be further improved by making a provision for deleting “any coach” of the r-Train (not only the last coach as in case of conventional r-Train). However, a coach will be deleted only when it has no non- ɛ elements stored in it. In the proposed approach after every insertion and deletion operation, the data is being sorted so that every data item comes in its proper place in an organized manner (ascending or descending). Since the sorting is done after the insertion or deletion operation, the end-user need not worry about the overhead involved. Furthermore, as we are getting a sorted data, the searching operation can be completed in an identical time complexity as in case of a binary search tree approach. The point to note here is, the data structure r-Train or Sorted r-Train are effective only when we have a huge amount of data or big data. If we have a limited amount of data, then using r-Train or Sorted r-Train will be an overhead to the programmer and thus should not be used.

The steps given below present the proposed modification. (We are assuming that the length of the larray is ‘r’ (just to present a generalized approach))

• 1.    Let “BEGIN” be the address of the first Coach (C 1 ).

• 2.    Create the first Coach C₁ with all ‘larray’ items in it as “ɛ” elements and “add₁” as the address pointing to an invalid value (since C1 is the only coach we have at this point of time).

• 3.    Find the “tagged coach (TC₁)” of the coach C₁

An example of this type of coach will be

C 1 = < ɛ1, ɛ2, ɛ3, ɛ4, ......... ɛr, add 1 >

• • TC₁ = (C₁, s), where “s” denotes the “status of the coach C₁”. At this point of time the value of “s” will be equal to “r”, since all the elements in the coach C 1 are “ɛ” (null elements).

Let us assume that we have the indices first, mid and last, wherein first denotes the index location of the first non- ɛ element of the larray, last denotes the index location of the last but one element of the larray and mid denotes the index location of ((first +last)/2) of the larray. (Point to note here is that the elements at these locations (first, mid, or last) can be ‘ɛ’ as well)

• A. Insertion Operation

The “insertion operation” in the “Sorted r-Train” can also be of two types as we have in case of classical “r-Train” data structure.

• i.    Insertion of a “New data item” in a “Coach”.

• ii.    Insertion of a “New Coach” in the “Sorted r-

• Train”

• a.    Insertion of a “New data element” in Sorted r-Train

The insertion of new element is done as per the following algorithm:

Algorithm: LA_Insertion

Let the Status of Coach (C) = Number of “ɛ” elements in the Coach and let the Length of Coach (C) = Number of Elements that can be stored in the coach = K

• 1.    FOR each New Element, DO

• 2.    FOR Each Coach in the Sorted r-Train, DO

• 3.    If Status (S) of Coach (C) = 0

• a. Print “ Coach Full, Check the status of Next Coach for Insertion

• 4.    END IF

• 5.    If status (S) of Coach = Length of Coach (K)

• a.    Insert the Element at LA[0] (First location in the Larray) in the Coach

• b.    Update the Status of the Coach as S= S-1

• 6.    END IF

• 7.    Else if (0

• a.    Loc= SearchLocation(LA) (Location where the new element will be inserted

• b.    Insert (LA, element, Loc) // insert the element at location Loc

• c.    Sort (LA) // Sort the larray

• d.    Update the Status of the Coach as S= S-1

• 8.    End ELSE IF

• 9.    END FOR

• 10.    END FOR

Function: SearchLocation(LArray)

int SearchLoc(LA)

{ return (LA.IndexOf(ɛ)) // returns First index of ‘ɛ’ in the larray }

Let us take few exmple for showing the insertion opertation.

• Example 1:

Let the given larray be

LA = < 3, 5, 7, ɛ, 26, 32, 39, ɛ, add >

We can easily find out the following:

Size of the larray = 8 (No. of elements in larray)

Status of the Coach = 2 (No. of ‘ɛ’ elements in larray)

Index of larray element ‘3’ = 0

Index of larray element ‘5’ = 1

Index of larray element ‘7’ = 2

Index of larray element ‘ ɛ ’ = 3

Index of larray element ‘26’ = 4

Index of larray element ‘32’ = 5

Index of larray element ‘39’ = 6

Index of larray element ‘ ɛ ’ = 7

Since Status (S) of Coach is > 0, we can insert the element in this coach.

Location (index) for insertion = SearchLocation(LA) = 3

Let the element to be inserted is ‘4’.

Therefore ‘4’ will be inserted at index 3 of larray.

So, the larray after insertion becomes

LA = (LA) = < 3, 5, 7, 4 , 26, 32, 39, ɛ, add >

Now, sort the larray to get the final larray after insertion

Therefore LA = <3, 4 , 5, 7, 26, 32, 39, ɛ, add >

This completes the insertion operation

• Example 2:

Let the given larray be

LA = < 9, 12, 17, 19, 38, 39, 45, 90 ɛ, add >

From the larray above, we can easily find out the following:

Size of the larray = 9 (No. of elements in larray)

Status of the Coach = 1 (No. of ‘ɛ’ elements in larray)

Index of larray element ‘9’ = 0

Index of larray element ‘12’ = 1

Index of larray element ‘17’ = 2

Index of larray element ‘ 19 ’ = 3

Index of larray element ‘38’ = 4

Index of larray element ‘39’ = 5

Index of larray element ‘45’ = 6

Index of larray element ‘90’ = 7

Index of larray element ‘ ɛ ’ = 8

Since Status (S) of Coach is > 0, we can insert the element in this coach.

Location (index) for insertion = SearchLocation(LA) = 8

Let the element to be inserted is ‘14’.

Therefore 14 will be inserted at index 8 of larray.

So, the larray after insertion becomes

LA = < 9, 12, 17, 19, 38, 39, 45, 90, 14 , add >

Now, sort the larray to get the final larray after insertion

Therefore LA = <9, 12, 14 , 17, 19, 38, 39, 45, 90 add >  This completes the insertion operation

• Example 3:

Let the given larray be

LA = < 13, 25, 77, ɛ, ɛ, ɛ, add >

From the given larray, we can easily find out the following:

Size of the larray = 6 (No. of elements in larray)

Status of the Coach = 3 (No. of ‘ɛ’ elements in larray)

Index of larray element ‘13’ = 0

Index of larray element ‘25’ = 1

Index of larray element ‘77’ = 2

Index of larray element ‘ ɛ ’ = 3

Index of larray element ‘ ɛ ’ = 4

Index of larray element ‘ ɛ ’ = 5

Since Status (S) of Coach is > 0, we can insert the element in this coach.

Location (index) for insertion = SearchLocation(LA) = 3

Let the element to be inserted is ‘44’.

Therefore ‘4’ will be inserted at index 3 of larray.

So, the larray after insertion becomes

LA = (LA) = < 13, 25, 77, 44 , ɛ, ɛ, add >

Now, sort the larray to get the final larray after insertion Therefore LA = <13, 25, 44 , 77, ɛ, ɛ, add >

This completes the insertion operation

• b. Insertion of new coach at the end in Sorted r-Train

This is very much similar to the insertion technique of r-Train data structure by R. Biswas [1]. Let the new coach to be inserted is Ck+1, perform the following steps to insert this coach in the Sorted r-Train

• 1.    Create the new Coach C k+1 with all ‘r’ larray items in it as ‘ɛ’

An example of this type of coach will be

Ck+1 = < ɛ1, ɛ2, ɛ3, ɛ4, ......... ɛr , addk+1>

• 1.    Update the pilot (linked list)

• 2.    Update the address part of the Coach C_k and assign the address of Coach C_k+1 to it.

• 3.    Set the address part of Coach C k+1 to an invalid address value.

• 4.    Set the status of Coach C k+1 = r.

• B. Search Operation

Let us assume that we have a Sorted r-Train as

T = < (C 1 ,S c1 ),(C 2 ,S c2 ),(C 3 ,S c3 ),...,(C i ,S ci ) ... (C k , S ck ) >

Where the coach C_i is (LA_i , add_i) where “LA_i” is the larray and “add_i” stores the “address of the next coach C i+1 ” or an “invalid address” in case C i is the last coach (when i= k ) and S ci denotes the “status of coach C i ”, for i = 1,2,3…k.

Let the element to be searched is “num”.

There can be two cases when we want to search for a particular element ‘num’

• 1.    When we know the coach number of ‘num’, we can directly go to that coach by visiting the pilot and perform “binary search” on that coach to match the elements of larray with ‘num’.

• 2.    When the coach number is not known, we will proceed in the following manner

• • Start from the first coach C1, and perform the operations given below till the element is found.

Let ‘LA’ be a larray, ‘first’ and ‘last’ denotes the index location of first non- ɛ element and last but one element of the larray respectively (note that ‘last’ here means ‘length of the larray - 1’, as the last element of the larray is the address of the next coach which is not taken into account for these calculations)

The pseudo code for searching the element is given below:

Algorithm: LA_Search boolean LA_Search (LA, first, last, num)

• 1.      {

• 2.   mid=(first +last)/2;

• 3.    if (first >last) return false;

• 4.   found=false;

• 5.   if(LA[mid] = = num){

• 6.   Print (“Element Found at Location”+mid);

• 7.    return true;

• 8.}

• 9.   else if(A[mid] = = ‘ɛ’)

• 10.{

• 11.    found=Search(LA, mid+1, last, num);

• 12.}

• 13.    else if(LA[mid] > num){

• 14.    found=Search(LA, first, mid-1, num);

• 15.}

• 16.    else

• 17.{

• 18.    found=Search(LA, mid+1, last, num);

• 19.}

• 20.    return found;

• 21.}

Let us take few exmple for showing the search opertation.

• Example 1:

Let the given larray be:

LA = < 3, 5, 7, 4, 26, 32, 39, ɛ, add >

Let the element to be searched = 4

Now from the given larray, we can find first and last indexes.

first = 0

last = 7

mid = (first +last)/2

= (0+7)/2

= 3

Now check if (4 = = LA [mid])

• i .e Is (4 = = LA [3]), YES, Since LA [3] = 4

Therefore element Found at index 3. The search operation successfully completes here.

• Example 2:

Let the given larray be:

LA = < 13, 25, 37, 46, 60, ɛ, add >

Let the element to be searched = 60

Now from the given larray, we can find first and last indexes.

first = 0

last = 5

mid = (first +last)/2

= (0+5)/2

= 2

Now check if (60 = = LA [2])

Is (60= = LA [2]), NO, Since LA [2] = 37

Now we will find new value of low (index) as low = mid+1

Therefore, low = 2+1 = 3

mid = (3+5)/2 = 4

Is (60 = = (LA [4]), YES, Since LA [4] = 60

Therefore element found at index 4. The search operation successfully completes here.

• C. Deletion Operation

We can have the following three types of “deletion operations” in the proposed “Sorted r-Train” analogous to classical “r-Train” [1, 2].

• 1.    Deletion of the data item from a Coach in the Sorted r-Train (here deletion operation refers to replacing the value of the deleted item with “ɛ”).

• 2.    Deletion of the last Coach of Sorted r-Train

• 3.    Deletion of a Coach from between the Two Coaches

• a.    Deletion of the data item from a coach (C)

• 1.    Let the element to be deleted is “k”

• 2.    If the coach number of the element “k” is known, we will directly go to that coach by accessing the pilot and search for “k” using search technique as discussed in previous section (Searching operation).

• 3.    After finding “k” within the coach, we will replace its value by “ɛ”. And change the status of the coach as s = s+1 (An important point to note here is, deletion operation does not have any effect on the size of the coach.)

• 4.    Sort the larray (LA) (so that all ‘ɛ’ elements comes at the beginning of the larray)

• 5.    If the coach number of the element “k” is not known, we will start from the first coach C 1 say, and search for the element “k” using the search technique discussed in above section (searching technique)

• 6.    After finding ‘k’ within any coach C_i (for i= 1, 2, 3, .... n) we will replace its value by “ɛ”.

• 7.    Sort the larray (LA)

• 8.    Change the status of the coach C i as s= s+1

The sorting of elements after every deletion operation ensures that all the ‘ɛ’ elements are always present in the beginning of the larray, this makes the process of insertion and searching less complex.

• b.    Deletion of the last Coach of Sorted r-Train

The deletion of a coach “C i ” is possible if and only if it is an empty coach (i.e all the elements in the coach are “ ɛ ” elements, as depicted here under in Fig. 5)

£

£

£

£

£

£

Invalid Address

Fig.5. An example of an “Empty Last Coach” of an r-Train

For deleting the last coach C i , of a Sorted r-Train, we proceed as follows:

• a)    Update the address “add i-1 ” of the coach “C i-1 ” by storing an “invalid address” in it.

• b)    Delete the “coach (C_i, r)” from the Sorted r-Train

• c)    Update the pilot.

  Coach (Ci, Sci)

  Coach (C2, 802)

  Coach (C3, SC3)

  Coach (См, Sen)

  Coach (Ci, Sa)

  Fig.6. (a) An r-Train before deletion operation

  
  

  Coach (Ci, Sei)

  Coach (C2, Sc2)

  Coach (C3, Зез)

  ■  ■  ■  ■

  Coach (Ci-1, Sei-1)

  Fig.6. (b) An r-Train after deletion operation is performed

  
  

It can be observed from the above Fig. 6(a) and Fig. 6(b) that the coach (C i ,Sc i ) has been deleted.

• 1)    Deletion of a Coach that lies between the Two Coaches in the Sorted r-Train

For deleting the coach ‘Ci’, of a Sorted r-Train which is between Ci-1 and Ci+1, we proceed as follows:

• a)    Update the address “add _i-1” of the coach “C_i-1” by storing the address of “C_i+1” in it.

• b)    Delete the coach (C_i, r) from the r-Train

• c)    Update the pilot.

  

  Fig.7. (a) An r-Train before deletion operation

  
  
  
  
  

Fig.7. (b) An r-Train after deletion operation

Fig. 7(a) and Fig. 7(b) given above shows the deletion operation. Here the Coach C i has been deleted from the r-train.

• V. Conclusion

The data structure “r-Train” proposed by R. Biswas [1] is a dynamic and highly scalable data structure which can be used for handling big data in an efficient and effective manner. As mentioned in [29], the “r-Train” data structured can be very successfully used for processing the data in parallel for executing various tasks. The proposed modification “Sorted r-Train” has further improved the time required for searching an element stored in the “r-Train” data structure. As the data is being stored in a sorted manner, we can very effectively apply binary search technique (which runs in O (log (n)) time in the worst case) in order to search the data items [30]. Moreover, deletion of any coach is made possible by just adjusting the address fields of the previous and next coach of the deleted coach (analogous to Linked list [30, 31]). The proposed approach of Sorted r-Train data structure can be used to store data generated from IoT devices as it requires real-time analysis and processing.

With Sorted r-Train, the data storage and retrieval time can be reduced to a greater extent as compared to the classical r-Train data structure. With the intricate and heterogeneous nature of big data, it is imperative to device new techniques and approaches for effective handling of these huge datasets. Sorted r-Train is an attempt towards the same. In future, the application of sorted r-train data structure for storing big data generated from IoT devices can be explored in order to perform real time query processing and analysis.