Совершенствование методики преподавания стереометрии и начертательной геометрии

Для развития пространственного мышления учащихся школы особенно эффективны многофигурные задачи в стереометрии, которые представляют собой аналоги простейших конструкций [1]. При решении таких задач возникают трудности не только у школьников, но и у студентов. Использование метода проекций и средств компьютерного моделирования помогает в создании чертежа, при выполнении решения и, главное, развивает интерес к стереометрии и начертательной геометрии.

Приведем одну из таких стереометрических задач [2].

Условие задачи

«На плоскости лежат четыре равных шара, причем три из них попарно касаются друг друга, а четвертый шар касается двух из этих трех. На эти шары сверху положены еще два равных шара меньшего радиуса, касающихся друг друга и трех больших шаров. Найти отношение радиусов большого и малого шаров».

Для решения задачи рекомендуется использовать вид сверху на конструкцию из шести шаров (рис. 1) [3, 4].

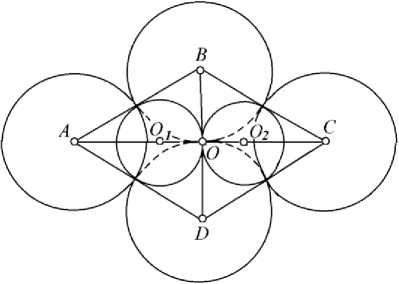
Рис. 1. Вид сверху на шары

Рассмотрим равносторонние треугольники ABC и BCD, которые принадлежат одной плоскости. Центры O1 и O2 малых шаров равноудалены от центров больших шаров, поэтому проекции точек O1 и O2 будут расположены в плоскости треугольников ABC и BCD. Следовательно, проекции малых шаров являются окружностями, вписанными в треугольники ABC и BCD. Примем радиус больших шаров равным R, а малых – r. Определим радиус малых шаров: r =

R _R

. Окончательно, =   3 .

3 r

Приведем этапы создания модели к задаче в среде программы Inventor [5]:

• 1    – в режиме «эскиз» были начерчены четыре окружности (рис. 2);

• 2    – после принятия эскиза в режиме «модель» с помощью команды « вращение » получены четыре шара (рис. 3).

• 3    – с помощью « рабочих плоскостей » в режиме «эскиз» , а затем в режиме « модель» были получены еще два шара (рис. 4).

  

  Рис. 2. Построение

  окружностей

  операцией « вращение »

  к задаче

  
  

  Рис. 3. Создание шаров

  
  

  Рис. 4. 3D-модель

  
  

Построение разверток поверхностей таких геометрических фигур как призма, пирамида, цилиндр и конус входит и в школьную программу по геометрии и в университетскую программу по начертательной геометрии. Кроме того и в инженерной практике развертки поверхностей необходимы при конструировании и изготовлении тонкостенных деталей сложной формы. Ниже приводятся примеры построения разверток с использованием метода проекций и компьютерной программы GeoGebra, содержащей достаточно большой набор инструментов для создания всевозможных геометрических образов и манипулирования этими образами на плоскости и в пространстве. На рис. 5 приведено построение развертки граней треугольной пирамиды методом проекций.

Большой интерес вызвала у школьников и студентов система динамической геометрии Geogebra, с помощью которой удается достаточно быстро и очень наглядно выполнять построение разверток поверхностей (рис. 6) [6].

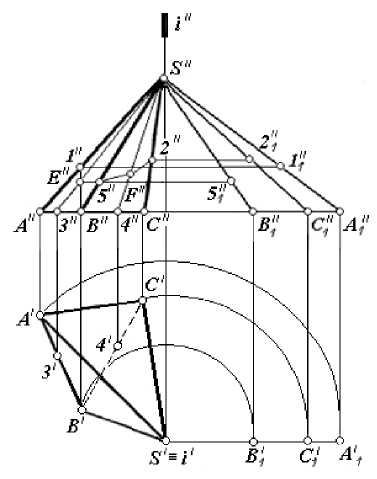
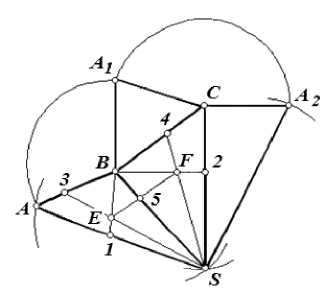
Рис. 5. Построение развертки пирамиды методом проекций

Благодаря организации в школах инженерных классов увеличилось количество участников конкурсов проектов, возрос интерес к инженерной профес сии.

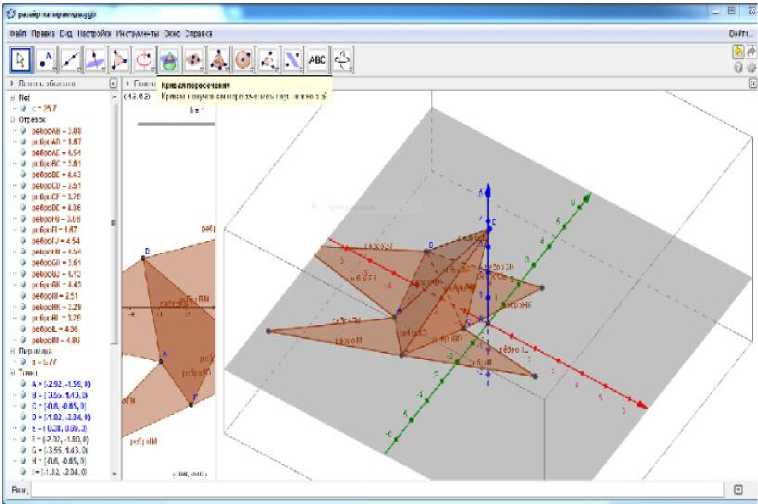
Рис. 6. Построение развертки пирамиды в среде программы Geogebra

Выводы

• 1.    Решение многофигурных стереометрических задач методом проекций помогает лучшему представлению взаимного положения фигур и развивает пространственное мышление.

• 2.    Приведенная методика преподавания стереометрии и начертательной

• 3.    Благодаря использованию программ 3D моделирования повышается интерес к изучению стереометрии, начертательной геометрии, а также к профессии инженера.

геометрии повысила творческую активность школьников и студентов.