Совершенствование методики решения задач на проценты в рамках формирования математической грамотности учащихся
Автор: Ковалева Г.И., Десятериченко М.А.
Журнал: Учебный год.
Рубрика: Функциональная грамотность
Статья в выпуске: 1 (75), 2024 года.
Бесплатный доступ
В статье представлены результаты выполнения учащимися заданий на проценты, причины их затруднений при решении, методические рекомендации по совершенствованию методики преподавания данной темы в контексте формирования функциональной грамотности учащихся.
Процент, метапредметность, функциональная грамотность, типы задач на проценты
Короткий адрес: https://sciup.org/14133589
IDR: 14133589
Текст обзорной статьи Совершенствование методики решения задач на проценты в рамках формирования математической грамотности учащихся
Важное место среди метапредметных образовательных понятий, которые осваивают обучающиеся в школе в рамках различных предметных областей, занимает такая социально-экономическая категория как процент.
Процент как специальный способ выражения доли величины применяется при изучении различных объектов, явлений, процессов на уроках математики, физики, химии, географии, биологии, информатики, технологии и пр. На занятиях школьники рассматривают процент как относительный показатель структуры (например, какую долю в общем объеме составляет величина), как относительный показатель динамики и сравнения (например, во сколько раз увеличилось значение величины по сравнению с предыдущим периодом) и пр.
В соответствии с федеральной образовательной программой основного общего образования знакомство с процентом на уроках математики происходит в 6-м классе в разделе «Дроби» содержательно-методической линии «Числа и вычисления» как продолжение изучения десятичной дроби. В этом же классе дети осваивают простейшие типы задач: на нахождение процента от величины, на нахождение величины по ее проценту, на выражение отношения величин в процентах. В м классе на базовом и повышенном уровне нарабатывается навык решения задач, в том числе и практикоориентированных, в рамках линии «Числа и вычисления». В 8-9-х классах данная тема продолжается в темах линии «Числовые последовательности и прогрессии» [1].
Умение решать задачи на проценты является универсальным инструментом при решении жизненных ситуаций: при расчете скидки в магазине, при начислении штрафов, налоговых вычетов и пр. Поэтому данное понятие входит в изучение всех содержательных областей финансовой грамотности школьников: «Деньги», «Доходы и расходы», «Семейный бюджет», «Покупки», «Личные сбережения и финансовое планирование», «Финансовая безопасность», «Страхование», «Инвестирование», «Кредитование», «Защита прав потребителя» [2, с. 3].
Несмотря на включение данной темы и в урочную, и во внеурочную деятельность школьников, к сожалению, результаты оценочных процедур (ЕГЭ, ОГЭ, ВПР) показывают недостаточный уровень овладения обучающимися школы умениями решать задачи на проценты.
Представим некоторые результаты выполнения заданий ВПР, ОГЭ, ЕГЭ по математике (рис.1).
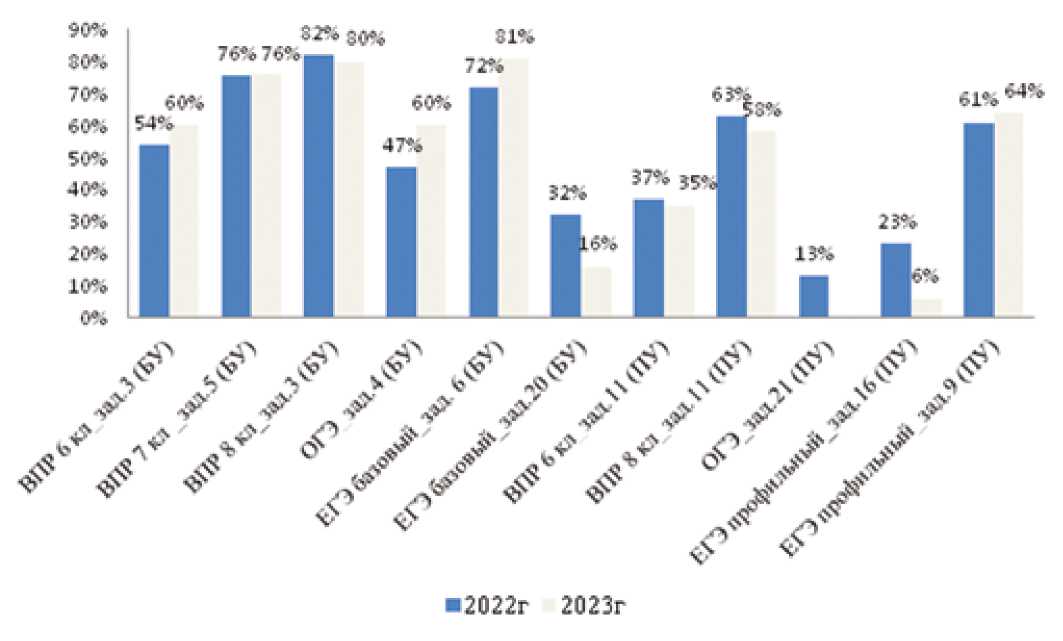
Рис. 1. Результаты выполнения заданий на нахождение процента в ВПР, ОГЭ и ЕГЭ по математике за 2022-2023 гг. (в %)
Как видно из рис. 1, шестиклассники испытывают большие затруднения при выполнении задач на проценты (справились только 54% в 2022 году, 60% в 2023 году). В 7-8-х классах доля обучающихся, справившихся с простейшими задачами уже больше, составила 76% и 80% соответственно. Также высокие значения продемонстрировали одиннадцатиклассники при выполнении задания № 6 ЕГЭ базового уровня.
А вот практико-ориентированные задачи, не сводящиеся к прямому применению алгоритма, а умению применить математические знания в простейших практических ситуациях даются учащимся совсем непросто. Так, 40% девятиклассников на ОГЭ не справились с контекстными заданиями социально-экономической направленности (задание № 4), а с текстовой задачей повышенного уровня (задание № 21) и того меньше – 13%.
Зианце MU (ОГ^МЗД. Используя данные палицы «структур* шкешк ппмцвда и РФ в 201S гл, определите др™ (в %) пкемоН площади зерновых и мрыововЬкх культур ■ оСшсй нкевноа плмцд* Полученный рсзуШЯТ округлите до целого числа
Если посмотреть на результаты ЕГЭ базового уровня, то с текстовой задачей № 20 на простые проценты справилось лишь 16% одиннадцатиклассников, задание ЕГЭ профильного уровня № 16 на сложные проценты решили в этом году всего 6% выпускников.
Умение решать задачи на проценты оценивается не только во время ВПР, ОГЭ и ЕГЭ по математике. Например, такие задачи встречаются и в оценочных процедурах по химии: в ВПР 8 класса (задания № 5, № 6.4), в ОГЭ – в заданиях № 18, № 22, в ЕГЭ – в заданиях № 26, № 28, № 34.
В задании № 13 ОГЭ по географии нужно найти процент от числа. В 2023 году с этим заданием справились только 55% девятиклассников. Пример задания приведен на слайде 1.
Слайд 1. Пример задания ОГЭ по географии на нахождение процента
|
<'1руктл]ы поенных пдощадеПя IM’R 1О1б г. Омн. п) |
|
|
ГЮМйнИ площадь |
ИЦВ |
|
В ТОм ЧИСЛО |
|
|
ЮрмрвЬОС и Э«рмоб<1фо«ь>х культур |
MJ |
|
MXWtHKUU KVFhiYp |
1ЦД |
|
кяртофопя и «юик» бехчепых культур |
13 |
|
кфМОвьЛ к.у Ль г ур |
1Z5 |
Опишем один из вариантов задания № 23 ОГЭ по биологии 2023 года, где требуется математически обосновать выбранное решение. В этой задаче девятиклассники должны продемонстрировать умения находить процент от величины и отношение величин в процентах: «Федор, нападающий в футбольном клубе, после вечерней игры, во время которой он провел на поле 80 минут, посетил кафе быстрого питания и заказал себе на ужин следующие блюда: плов с курицей, салат мясной и апельсиновый сок. На сколько заказанный ужин компенсирует энергозатраты матча (в %)?».
К тексту задания прилагались две таблицы: первая – с данными энергозатрат при различных видах физической активности, в том числе и при занятиях футболом, вторая – со сведениями энергетической и пищевой ценности продукции кафе быстрого питания. Обучающиеся должны были найти по таблицам соответствующие значения, затем сделать вывод на основе расчетов, компенсирует ли заказанный ужин энергозатраты или нет. С этим заданием по биологии справились всего 23% участника.
Нетрудно заметить, что если условия задачи представлены в явном виде, то учащиеся их решают достаточно успешно, но если текст нужно интерпретировать, поработать с таблицами, графиками, диаграммами и пр. и только затем построить математическую модель, возникают сложности.
Какие же методические проблемы лежат в основе неудач освоения обучающимися данной темы?
Во-первых, сокращение или искажение этапов формирования понятия. При всей кажущейся простоте темы «Процент», этапы формирования понятия довольно сложны, т.к. обучающиеся должны обладать достаточным уровнем абстракции и развитым наглядно-образным мышлением.
Во-вторых, отступление от принципов изучения базовых тем – неоднократность, последовательность и поступательность. В 6-8-х классах педагоги еще уделяют внимание решению задач на проценты, а в выпускных классах только на этапе подготовке к экзаменам. Отсутствие поступательной системной работы над формированием понятия и овладением способами решения задач на проценты приводит к тому, что обучающиеся не понимают, как использовать этот универсальный инструмент ни на школьных занятиях, ни в жизни.
В-третьих, обучающиеся недостаточно владеют приемами работы с визуальным и невизуальными текстами. Речь идет о недостаточном уровне развития функциональной читательской грамотности. Дети не умеют интерпретировать текст задачи и переводить его в известные им способы действия. Причины кроются в сложности восприятия грамматических конструкций текста. Для таких учащихся тексты оказываются недостаточно понятными, так как большая смысловая и математическая нагрузка в задачах на проценты падает на предлоги, наречия и устойчивые словосочетания, посредствам которых и выстраивается логика ситуации, отраженной в задаче. Следует попрактиковаться в визуализации текста, научиться отображать описанную ситуацию в схеме, рисунке, таблице, что позволит правильно построить математическую модель задачи.
В-четвертых, учащиеся не владеют основными алгоритмами решения задач на проценты. К основным типам таких задач относятся: нахождение процента от величины; нахождение величины по ее проценту; выражение отношения величин в процентах; практико-ориентированные задачи, в том числе социально-экономической направленности; задачи на простые и сложные проценты.
В рамках совершенствования преподавания данной темы предлагаем придерживаться следующих этапов формирования понятия и обучения решению задач на проценты.
Первый этап. Сформировать понимание процента, выработать умение выражать процент соответствующей обыкновенной дробью.
В «Статистико-аналитическом отчете о результатах государственной итоговой аттестации по образовательным программам основного общего образования в 2023 году в Волгоградской области» указано на то, что учащиеся должны понять: процент – универсальная величина измерения, которая появилась из практической необходимости измерения и сравнения различных величин [3, с. 35-36].
Не должно быть никакой спешки и форсирования при усвоении понятия. Надо неоднократно повторить одно и то же действие: найти 3/100 от а, 15/100 от b, 31/100 от c, 103/100 от m и пр., заметить, что сначала нужно найти одну сотую часть числа, а потом умножить на количество сотых. Когда число делят на сто, говорят, что находят 1% числа, в нашем случае, нашли 3% от а, 15% от b, 31% от c, 103% от m и пр. И только после этого вводится определение процента.
Далее нужно научить переводить задачи с языка дробей на язык процентов и наоборот: 25% величины – это ее четверть, половина величины – это 50%, 30% величины больше ее четверти, вся величина – это 100% и пр. Обязательные приемы: закрашивание, вырезание, использование рисунков, таблиц, схем для визуализации долей величины и пр.
Второй этап. Перенос правил нахождения дроби числа и числа по его дроби с действиями на проценты. Действия одни и те же, но звучать по-разному. В первом случае речь идет про числитель и знаменатель, во втором случае – про количество процентов. Необходимо провести сопоставление и обобщение.
Третий этап. Изучение процентов прочно связать с десятичными дробями: обобщаем, учим бегло переводить обыкновенную дробь в десятичную, в проценты, а проценты – в обыкновенную и десятичную дробь.
Четвертый этап. Решение задач на процентное содержание, задачи на растворы, смеси и сплавы, решение социально-экономических задач. Главная работа этого этапа – составление математической модели текстовой задачи (таблица 1).
Сначала по действиям решаем задачи, в которых некоторая величина а увеличилась (уменьшилась) на r% ; выясняем, что все задачи решаются одинаково – у них одинаковая арифметическая модель. В совместной деятельности обобщаем, выводим формулу, строим алгебраическую модель задачи.
Таблица 1. Составление арифметической и алгебраической модели задачи на простые проценты

В результате используем формулу при решении задач:
– число а увеличилось на 10%, получилось 1,1а;
– число а уменьшилось на 10%, получилось 0,9а и пр.
Привлекаем внимание к обратным задачам: например, было – а, стало – 3а, на сколько процентов увеличилось? На 200%.
Пятый этап. Совершенствование умений решать задачи на проценты различными способами, рассматриваются задачи на концентрацию, кредиты, в том числе отработка задач на простые и сложные проценты.
Занятие следует посвятить решению системы задач на проценты. Сначала решается обычная «готовая» задача, затем составляются и решаются различные обратные задачи (посредством групповой, индивидуальной, самостоятельной работы и пр.). Далее переходим к составлению и решению «родственных» задач, поощряя их практико-ориентированный контекст, и, наконец, самостоятельное составление обучающимися кейса с заданиями на проценты с использованием, таблиц, графиков и пр.
Рекомендуем с четвертого этапа использовать в образовательном процессе задания, разработанные в рамках проекта «Мониторинг форми- рования функциональной грамотности учащихся» из разделов математической и финансовой грамотности: matematicheskaya-gramotnost/ [4].
Советуем в рамках внеурочной деятельности проводить в школе «Дни Процента», когда на всех уроках так или иначе учащиеся сталкиваются с данной тематикой и решают простые и сложные задачи.
Таким образом, педагогам важно понимать, что освоение данной тематики вносит особый вклад в формирование предметных и метапред-метных образовательных результатов. Нужно ознакомить и отработать с учащимися всю палитру способов решения задач на проценты: предметный, арифметический, алгебраический, геометрический, с учетом разного уровня предметной подготовки.
Для детей с низким уровнем обученности прочное овладение предметного и арифметического способа решения задач на проценты будет хорошим инструментом при решении учебных и жизненных задач. Нужно добиваться, чтобы учащиеся со средним уровнем применяли как арифметический, так и алгебраический способ решения. Учащиеся с высоким уровнем обученности должны быть вооружены всем арсеналом методов и знать условия и риски их применения. Литература в помощь учителям
(тема «Проценты» и формирование математической грамотности)
-
1. Приказ Министерства просвещения РФ от 18.05.2023 № 370 «Об утверждении федеральной образовательной программы основного общего образования». – URL: https://static.edsoo.ru/projects/upload/FOP_OOO.pdf .
-
2. Рутковская, Е.Л. Финансовая грамотность / Е.Л. Рут-ковская, Н.В. Штильман, А.А. Бочихина [и др.] // Методические рекомендации по формированию функциональной грамотности обучающихся 5-9 классов с использованием открытого банка заданий на цифровой платформе по шести направлениям функциональной грамотности в учебном процессе и для проведения внутришкольного мониторинга формирования функциональной грамотности обучающихся / под ред. Г.С. Ковалевой. – М: ФГБНУ «Институт стратегии развития образования РАО», 2022. – 360 с. – URL: https:// edsoo.ru/Metodicheskie_rekomendacii_po_formirovaniyu_ funkcionalnoj_gramotnosti_obuchayuschihsya_5_9_ klassov_s_ispolzovaniem_otkritogo_banka_za.htm
-
3. Статистико-аналитический отчет о результатах государственной итоговой аттестации по образовательным программам основного общего образования в 2023 году в Волгоградской области. – URL: https://vgapkro.ru/wp-content/uploads/2023/09/volgogradskaya_sao-9-2023-glava-2-matematika.pdf
-
4. Методические рекомендации по формированию математической грамотности обучающихся 5-9-х классов с использованием открытого банка заданий на цифровой платформе / под ред. Г.С. Ковалевой, Л.О. Рословой. – М.: ИСРО РАО, 2021. – URL: http://skiv.instrao.ru/bank-zadaniy/ matematicheskaya-gramotnost/МГ_МетодическиеРеко-мендации_2021.pdf


