Спектр лапласиана в области с границей и барьером, составленными из малых резонаторов

DOI:

Задачи, связанные с влиянием геометрических возмущений границ области на спектр оператора, широко освещены в литературе [4; 7; 8; 10; 11; 13]. В частности, возмущения, связанные с подсоединением к области резонаторов Гельмгольца, привлекают интерес из-за резонансных эффектов полости, простоты описания, возможности физической реализации и большого количества разработанных методов исследования таких систем. Результаты получаются с использованием вариационных методов, анализа асимптотик [1; 2; 6; 9; 12; 25], а также приближенной модели точечных отверстий [16; 17; 19–23].

Существует множество областей практического применения теории возмущений резонаторами Гельмгольца, таких как наноэлектроника, использующая волноводы нанометрового масштаба, при котором проявляются квантовые эффекты, или акустические приборы, решающие такие задачи, как шумоподавление [3] и т. д. В частности, интересующие нас поверхности, заполненные большим количеством резонаторов, создающими особые граничные условия, в настоящее время активно исследуются в области метаматериалов [15; 26].

В данной работе рассматривается возмущение границы области присоединением N резонаторов Гельмгольца в пределе N ^ то . Системы, содержащие неограниченно возрастающее количество резонаторов, рассматривались в работах [9; 14; 18; 24]. Границы области с такими возмущениями часто называют гофрированными границами.

Работа организована следующим образом: во втором разделе рассматривается система с границей из N узких полос, для которой выводится предельное граничное условие, в третьем разделе аналогичный результат получается для системы с барьером из N резонаторов, разделяющим две области, и в четвертом разделе приводятся численные результаты для обеих систем, которые сопоставляются с аналитическими.

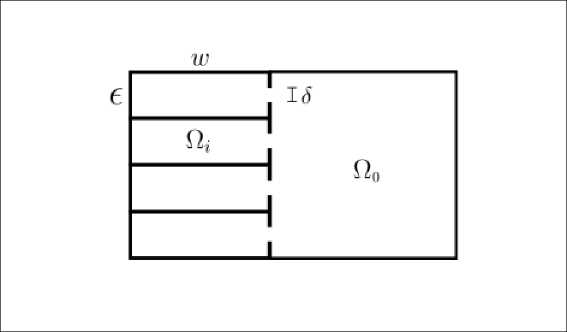
Рис. 1. Пример геометрии системы с гофрированной границей

1.    Граница из полос

Введем семейство областей Q^, где параметр N отвечает за количество присоединенных резонаторов (на рисунке 1 изображена область Ω4). Пусть Ω0 — односвязная прямоугольная область на плоскости R2, дQ — граница этой области. Левую часть границы области обозначим Г = {(ж,у)1ж = w} С дQ0, возмущение границы будет происходить на этой части. Вдоль границы Г, где через отверстия шириной 5 присоединяются N малых резонаторов Гельмгольца Q». Параметр е = |N характеризует расстояние между соседними отверстиями в границе Г, ведущими к резонаторам Гельмгольца. При увеличении N ширина резонаторов е и размер отверстий 5 стремятся к нулю, в то время как длина резонаторов w остается постоянной. Мы полагаем 5 = Ле, 0 < А < 1. На области Q^ определен оператор Лапласа с граничными условиями Неймана:

д 2и   д²и

^H n и := -^ЛN м = -тот? - тот?.

дж ² ду ²

Собственные значения оператора — Л _N с порядковым номером п обозначаются ^, а их собственные функции — Е У (ж), ж G R ² .

Далее мы будем работать в рамках приближенной модели точечных отверстий. Этот метод зачастую применяется для построения точных решений в случаях сложной геометрии, содержащей отверстия, размер которых мал по сравнению с длиной волны. Метод заключается в том, чтобы перейти к системе с геометрией, в которой конечные отверстия заменяются на точечные, а затем теория самосопряженных расширений симметрических операторов используется для построения параметризованного оператора, описывающего новую систему, причем его параметр к ₀ контролирует пропускную способность точечных отверстий и может быть подобран так, чтобы наиболее точно соответствовать ситуации с конечным диаметром отверстий.

Введем следующие обозначения: С(ж, ж » , к), С » (ж, ж » , к) — функции Грина с условиями Неймана в прямоугольнике, для областей Q 0 и Q » соответственно, с особенностями в точках отверстий ж » , а также д(ж » , к, к ₀ ), д » (ж » , к, к ₀ ) — вычисленные в точках отверстий функции, полученные из соответствующих функций Грина вычитанием сингулярностей:

дЛж » , к, ко) = [G . (ж, ж » , к) — £Дж,ж » , ко) _х^_х . .

Все малые резонаторы у нас идентичны, поэтому д » (ж » , к, к ₀ ) фактически зависит только от двух последних параметров и будет записываться как д(к,к ₀ ).

Приведем основной аналитический результат раздела.

Теорема 1. Пусть ^ N (ж),п = 1,2... — собственные функции возмущенного модельного оператора H _n из семейства, описанного выше.

• 1)    Функции ^ N (ж) имеют следующий вид:

. N ( _ж ) = Г Е^ 1 ^а ^ ^( ^ж , ^ж з , ^{к ) ж G Q} 0 ^П | - а г С » (ж, ж » , к)       ж G Q » ,

где коэффициенты удовлетворяют следующей системе из N условий:

N а»д(ж», к, ко) + У~^ ajG^i, ж,, к) = — а»д(к, ко),    г = 1,2, ...N.        (2)

3 =

• 2)    В пределе N ^ то функции ^ ^N (ж) сходятся к решениям следующего интегрального уравнения:

^ (ж) = — j ^(у)С(ж,у, к)к tan[кw]dу,

которое соответствует следующей задаче на собственные значения дифференциального оператора:

An + k²n = 0

* dk l r = - к tan(kw)n | r

Й |d Q o \ r = ⁰

Оставшаяся часть раздела посвящена доказательству теоремы.

Общая схема модели точечных отверстий на базу теории расширений операторов такова (см., например, [17; 20]). Стартуем с ортогональной суммы неймановских лапласианов в областях П _о , n _t , г = 1, 2 ...N . Сужаем этот оператор на множество гладких функций, зануляющихся в точках x _t , и замыкаем оператор. Получаем симметрический оператор с индексами дефекта (2N, 2N). Его самосопряженное расширение, которое и даст требуемую модель связи резонаторов через точечные отверстия, удобно строить, сужая сопряженный оператор. Область определения сопряженного оператора описывается через дефектные элементы G _t (x,x _t ,k‘0 ⁰ ) по теореме Неймана [5] (к^ <  0 — некоторое отрицательное регулярное значение оператора). В нашем случае она состоит из функций

( O i G i (x, x t , к°) + гр « (ж), x Е П^ ( a ^o G o (x,x t , к 2 ) + гр o (x), х Е П о ,

где G _t (x,x ₀ ,k) — функция Грина неймановского лапласиана в области n _t , p _t (x) — функции из области определения расширения по Фридрихсу данного симметрического оператора (то есть функции, не имеющие особенностей в точках x _t ). Учитывая характер функций p _t (x), получаем следующую асимптотику функций p (x) в окрестности точек x t :

( a t G t (x,x t , k 2 ) + b t + o( | x - x » | ), x Е n t , [ a 0 G o (x,x t , k 2 ) + b ⁰ + o( | x - x t | ), x Е П о .

Известны асимптотики функций Грина вблизи особенности:

G _t (x, x ₀ , k) = — In π

| x - x o l

+ e t + o( | x — x o | ).

Область определения самосопряженного расширения H _n выделяется с помощью удовлетворения условию ( H _n n,v) — (n, H _n v) = 0, n, v Е D ( H _n ). Мы не будем рассматривать все возможные самосопряженные расширения (то есть все возможные условия на коэффициенты), а выберем только одно, которое представляется наиболее естественным (это так называемое условие Кирхгофа):

a ⁰ = — a t , ь 0 =b t .

Отметим что построенный оператор параметризован вещественным числом к0 <  0.

Этот параметр определяет «пропускную способность» отверстия. Как было показано в

[20], модельный самосопряженный оператор наиболее хорошо соответствует случаю реального отверстия конечного диаметра d, если параметр выбирается следующим образом ко = 2^ exp(-Y), δ

где y = 0, 5772... — константа Эйлера.

Пусть к ² — собственное значение модельного оператора Н ^N , не являющееся собственным значением неймановского лапласиана в Q * и Q. Cоответствующая ему собственная функция имеет вид:

( ) = / Е ” =1 a^G(x,X J• , к), ж Е

Q, ^ _г .

”       [ а*” С * (ж,ж * ,к),        х Е

Отметим отличие этого выражения от общей формы элементов D ( H _n ) (6), где присутствуют произвольные функции с условиями Неймана й, и параметр к _о зависит только от размера отверстия, но не от энергии к ² .

Теперь, чтобы соотнести а , и а , и выразить условия (8) через а *”’^еж , мы должны выделить особенности С * (ж,ж * ,к _о ). Для каждого отверстия I сделаем следующее:

^(ж) =

ж Е Q, ж Е ^ i , ж Е П ; ,3 = I,

^^(ж, ж*, ко) + а^д^, ж*, к, ко) + Y^i af С(ж, ж;, к), < а^С^ж, жг, ко) + a^gt(ж, жь к, ко), а™ Gj(ж, ж;, к),

д*(ж, z, к, к _о ) = С^е(ж, z, к) — С^е(ж, z, к_о).

Сравнивая это с (6) и используя (7), мы получаем а^ = а*, г = 1, ...N, и условия (8) принимают следующую форму:

а * := а ^ = — а *” ,

N

а * д * (к, ко) + ^ а ; С(ж * , ж ; , к) = — а * д(к, к о ).                    (11)

j = *

Рассмотрим предел построенных функций при N > то . В частности, выведем предельное выражение для системы (11) условий на коэффициенты а * . С этой целью рассмотрим пределы функций Грина внутри резонаторов. Выпишем известное выражение для функций Грина уравнения Гельмгольца в прямоугольнике размеров w на h, с граничными условиями Неймана:

∞∞

^’^ ^ % Wh

п гж 1

cos---- w

П]ж2    niz1    njz21

cos —: cos cos —--37-.T^-v.

h       w       h к2 — ( * 2 n 2 + ^j 2 n 2 )

w2

В нашем случае имеем

∞∞

^{G ( ж,z, к )} = ^^

*=о ;=о a j cos n*^1 cos nj52 cos n*^1 cos nj^2 l,J        wew€

™^c     « 2 — (^ + eg ² )

Ci j = 2 2 ^{5 i 5 j}, 5i = < ^’      ®,    — Дельта-функция Кронекера.

,                               1, 2 = 0.

Подставляя h = е и переходя к пределу 22   22

предельных условий I Л^ =    +     :

е ^ то , мы получаем коэффициенты для

∞∞

9 . (к,ко) = 1 ££ ^ cos ^{2 е} 1=0 j = ^w

П7_____

2 (к ² -

^к 0

-

к2

Л^-)(к2 - Л^-).

Отмечая, что к 2 = — 5 2 , мы можем выразить предел д ^ш (к)dx = lim ^ , 0 е9 е (к, к ₀ ):

Г (к)е =

1     2, ул шк2 w к-^ i=1

(к ² - ^)’

используя следующую формулу для ряда:

∞

∑︁ ₂ i =1 ¹

-

а ²

2а ²

-

п cot(a n )

2а

.

Когда расстояние между отверстиями е ^ 0, ширина отверстий 5 ^ 0, и учитывая к ₀ = 2 i exp ( — y ) , к2 ^ -то , мы можем получить в явном виде формулы для предела:

^{cot кш}

9 ^{( к ) е} =     _к

.

Пусть

N

U i := u(x , ) = а 9 г (к, ко) + ^ a - G(x i , x - , к).

j = i

Условие (11) может быть представлено в виде

U i = - O i 9 _e (к, к о ).

Умножая каждое из этих N уравнений на G(x, x^) и суммируя, получаем

N               N

^2 а i G(x,X i ,к) = - ^U i G(x,x i , к)[9 _е (к, к о )е] ^-1 е.

i =1                         i =1

Левая часть этого выражения — оригинальная собственная функция, а правая часть содержит значения этой функции в точках отверстий, умноженные на расстояние между ними dx = е, что делает выражение интегральной суммой (с разбиением на равные отрезки длины е). Поскольку интеграл существует, способ разбиения не играет роли. Наконец, рассматривая предел N ^ то , мы получаем интегральное уравнение для некоторой функции u(x), действующей в области Q.

^ (x) = - ^ ^ (y)G(x, у, к)[9(к, к о ) dy] ¹ dy = = - j ^ (y)G(x, у, к)к tan[кw]dy.

Это интегральное уравнение эквивалентно следующей задаче на собственные значения с граничными условиями в области Ω 0 :

An + k²n = 0

* dk l r = - ^ tan(^w)u | r

| S Q \ r = 0.

Теорема доказана.

Замечание 1. Мы не рассматриваем здесь предельный переход в области, где находятся полосы.

2.    Барьер из полос

Далее мы расширяем данный метод на новый тип систем — возмущение в виде барьера из резонаторов.

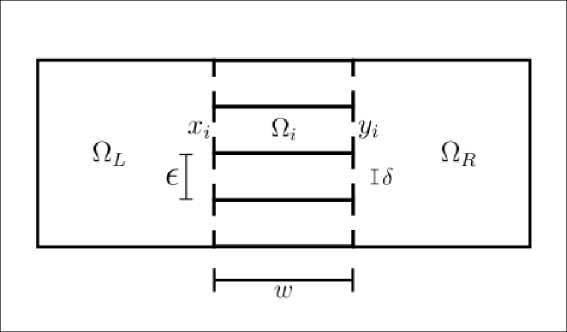
Рис. 2. Два квадратных резонатора, связанные через гофрированную границу из N (здесь N = 4) прямоугольных резонаторов, каждый из которых имеет два отверстия в точках ж и у

Общий вид системы с гофрированным барьером представлен на рисунке 2. Пусть Q _l , Q r — две непересекающиеся области в R ² с общей границей Г. Вдоль границы между основными областями вставляются N резонаторов Q i , г = 1, 2,...N (не изменяя формы областей, но сдвигая одну из них на необходимое расстояние). Каждый резонатор соединяется с обеими областями через два отверстия диаметра δ . Середины отверстий обозначаются ж _г , для отверстий из левой области Q _l , и у _г — из правой Q r (х _г ,у _г Е R ² ). Резонаторы имеют прямоугольную форму, со сторонами w и h = е = | N , последнее соответствует расстоянию между соседними центрами отверстий вдоль границы Γ в каждой из основных областей. Оператор на областях с возмущением и примененным приближением точечных отверстий обозначим H _n .

В данном разделе, аналогично предыдущему, мы получаем точные выражения собственных функций H _n и рассмотрим предел N ^ то . Как и во втором разделе, рассматривается форма малых резонаторов в виде полос с фиксированной длиной, w = const, h = е. Опуская вычисления, приведем основной результат:

Теорема 2. Пусть ^ N (x),n = 1,2... — собственные функции возмущенного модельного оператора Н _n из семейства, описанного выше.

1) Функции ^ ⁿ (x) имеют следующий вид:

Y " ₌₁ ^a j G ⁽ x,X j ^{,k )} ,

u _n (x) = <

- a G i (x, x _t , k) - e t G t (x, y i , k),

x E ^ _L ,

X E ^ i ,

E” =i e ^{G ( x,}y ₃ ^{,k )} ,

x E П д ,

где коэффициенты удовлетворяют следующей системе из 2N условий ( i = 1,2,... N ):

f a g ^L (k, ko) + ^ = a j G ^L (x i , x j , k) = - «^(k, k o ) - e i G(k), [ e i g f (k, k o ) + £^ e i G ^R (y i , y j , k) = — e i g(k, k o ) - a i G(k).

• 2)    В пределе N ^ то функции ^ⁿ (x) сходятся к ^(x) = решениям следующей пары интегральных уравнений:

  {u^L(x), x E ^_L, u^R(x),x E Пд,

  
  
3.    Численные результаты

{uL(x) = fT GL(x,y,k) [r-(k)u - r+(k)u] dy, uR(x) = JrGR(x, y, k) [-r—(k)U - r+(k)U] dy, которые соответствуют следующей задаче на собственные значения дифференциального оператора:

Au + k2u = 0, d^ |гд + d^ |rL = -r+(k)(uR + UL)|r, H^R |ря - d^r Irb = -r-(k)(uR - uL)u|r, 1^ |dQo\r = 0.

r - (k) =lim r » = ^k sin ^k ™ , 6 ^ o      cos kw - 1

k sin kw r+ (k) = lim r , = ------------.

6 ^ o ⁺ cos kw + 1

Численно были построены собственные функции систем с точной геометрией (то есть без приближения точечных отверстий).

На рисунке 3 приводятся два графика, на которых построено отношение производной собственной функции к ее значению как функция от собственной энергии состояния. Каждое значение получается следующим образом: отношение рассчитывается в N точках x _i + dx, и берется среднее арифметическое (с отбрасыванием 10 % экстремальных значений). Величина dx мала по сравнению с величиной отверстий, не изменяется и выбрана так, чтобы минимизировать разницу между собственной функцией, построенной из функций Грина (см. левую часть (2)), и численным значением функции. Все параметры системы неизменны, за исключением количества резонаторов и размера отверстия.

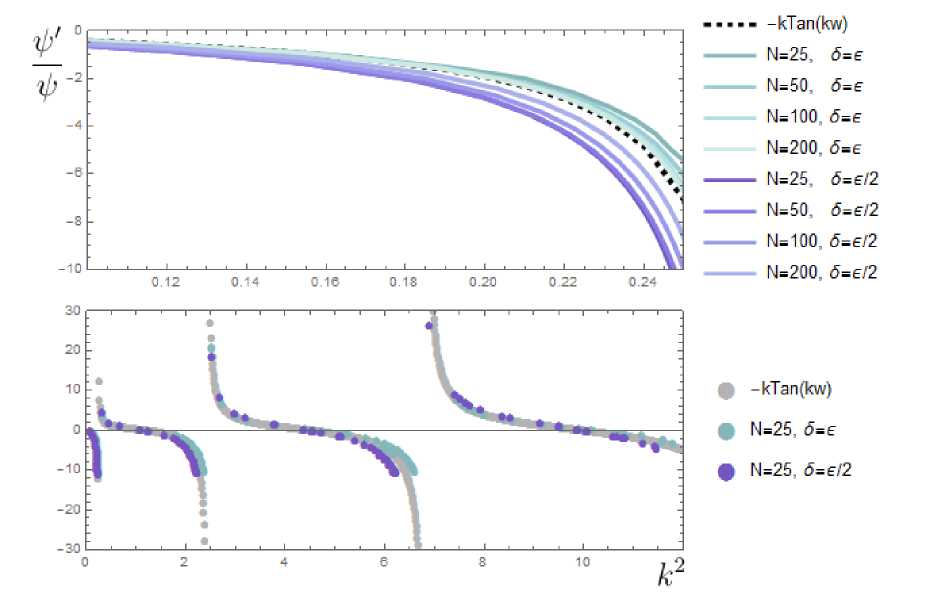
Рис. 3. Система с границей, гофрированной полосами. Графики отношения производной функции к ее значению, взятым вдоль возмущенной границы области Ω (среднее значение). Каждая линия соответствует фиксированной геометрии системы, с обозначенными параметрами N и 5 (остальные параметры неизменны). Сверху показаны два набора из четырех линий: для отверстий, равных половине ширины полос, и для отверстий, равных ширине полос (когда у малых резонаторов есть только боковые стенки, то есть это не резонаторы, а каналы). Нижний график частично повторяет верхний в другом масштабе. Каждая точка соответствует конкретной собственной функции, точки одного цвета — одинаковая геометрия системы, с обозначенными параметрами N и 5 (остальные параметры неизменны).

Также на графиках приведен теоретический предел — к tan kw , обозначенный пунктирной линией и серыми точками

Мы использовали модель точечных отверстий, поэтому наш результат применим к случаю с малым отверстием в стенке резонатора. На графике помимо этого случая приведены также результаты для случая с полностью отсутствующей стенкой Ω, претерпевающей возмущение, то есть полосы напрямую прикрепляются к основному резонатору. Как видно в масштабе нижнего графика, в случае отсутствующей стены сходимость к предельному значению — к tan few оказывается заметно лучше. Более того, данная закономерность распространяется на все размеры отверстий, то есть сходимость тем лучше, чем ближе 5 /е к единице.

На рисунке 4 изображены аналогичные графики для систем с барьером из 25-ти резонаторов (полос). Здесь не приводятся значения, соответствующие отношениям с малым знаменателем, так как в этих случаях погрешность при вычислении производных становится существенной по сравнению с самим значением. Серым изображены предельные функции, полученные аналитически. Как видно из рисунка, теоретически предсказанные асимптоты и нули присутствуют на численных графиках.

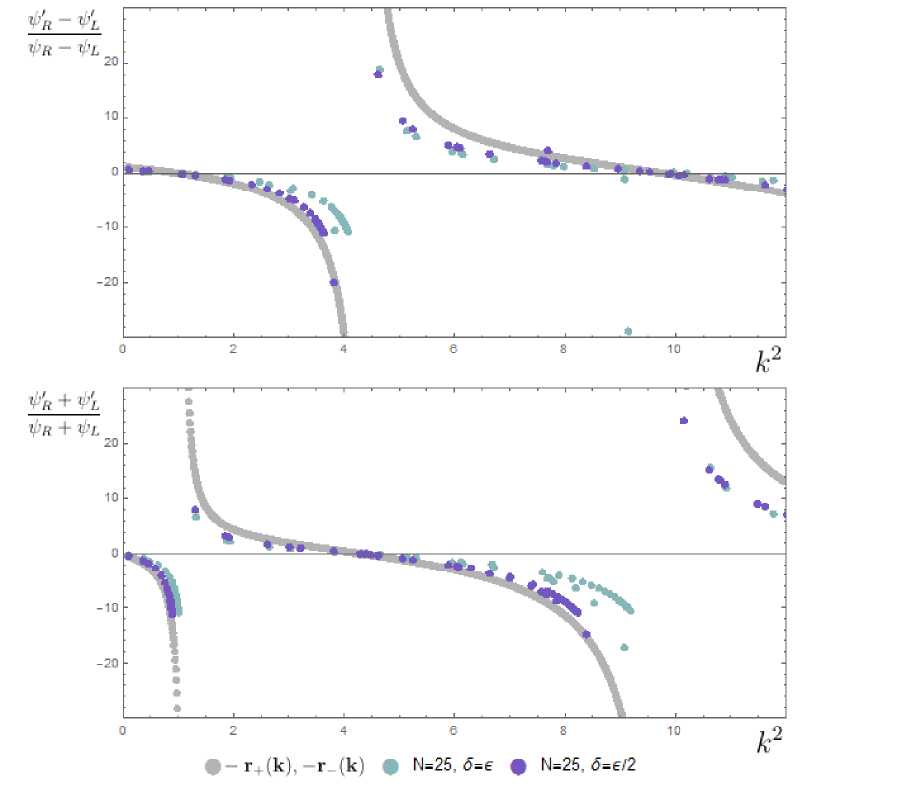
Рис. 4. Система с полупрозрачным барьером, гофрированным полосами. Графики отношения сумм и разностей производных функции на разных сторонах барьера к ее значениям. Каждая точка соответствует конкретной собственной функции, точки одного цвета — одинаковая геометрия системы, с обозначенными параметрами N и 5 (остальные параметры неизменны).

Показаны три набора точек: серые точки — теоретический предел, — г - ( к ) — сверху и

— г + ( к ) — снизу, остальные два набора — для отверстий, равных ширине полос, и для отверстий, равных половине ширины полос

Заключение

Вопрос о собственных функциях оператора Лапласа в ограниченной области возникает во многих физических задачах от акустики до наноэлектроники. При этом случай самых естественных граничных условий Дирихле или Неймана уже хорошо изучен. Однако в ряде ситуаций возникает потребность в необычных граничных условиях (например, для шумопоглощения). Их можно создать либо с использованием специальных материалов на границе, либо делая границу специальной сложной формы. В данной работе мы рассмотрели возмущение границы при помощи множества резонаторов Гельмгольца, присоединенных к основному резонатору через малые отверстия. В частности, нас интересовал предел при стремлении количества резонаторов к бесконечности.

В результате получается энергозависящее граничное условие.

Мы рассмотрели два типа систем — с границей из полос и барьером из полос. В обоих случаях были получены в явном виде граничные условия предельного оператора. Результаты проверены численно.