Спектральный анализ подвижностей атмосферных частиц

Инструментальный мониторинг атмосферных частиц на основе спектральных измерений размеров и подвижностей развивается в последнее время достаточно продуктивно. Интерес к изучению аэродисперсных систем быстро возрастает в связи с вредным воздействием частиц антропогенного аэрозоля на здоровье человека. Совместное изучение природных и антропогенных факторов, участвующих в образовании аэродисперсных систем, приводит в конечном итоге к расширению спектрального диапазона размеров частиц, который в большинстве случаев находится в пределах от 1 до 1000 нанометров.

Для нижней тропосферы над сушей крупных городов репрезентативным считается [1] так называемый континентальный тип одномодового (унимодального) распределения частиц по размерам, представленный на рис. 1. После резкого подъема до максимума около значения r = 0.01 мкм начинается медленный почти экспоненциальный спад плотности вероятности. Такое распределение соответствует хорошо известным [2] эмпирическим формулам общего вида f ( r ) = ar^p exp ( - br ) ( a,b, p,s — эмпирические константы), справедливым для большинства конденсационных и дисперсионных аэрозолей.

Отмечается [1], что концентрация больших частиц резко падает в самом нижнем слое тропосферы в несколько десятков или сотен метров. Отмечается также, что такое распределение имеет тенденцию сужаться как со стороны частиц малых

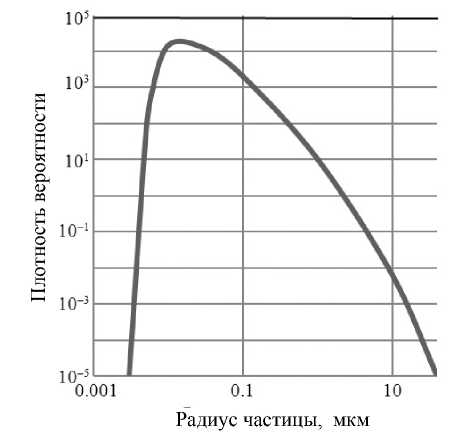
Рис. 1. Распределение по размерам частиц континентального аэрозоля размеров, так и со стороны больших частиц, а модальный размер — передвигаться с течением времени в сторону больших частиц.

ПОСТАНОВКА ЗАДАЧИ

Большинство динамических свойств аэрозольной системы определяется подвижностью частиц, зависящей от их размеров и электрического заряда. Доля частиц, имеющих заряд q=ne (n — це- лые положительные или отрицательные числа), в стационарном состоянии при симметричной биполярной ионизации описывается [2] больцма-новской функцией вида г ( \     - (ее )78 ПЕ^гкпТ f (е) = е( )    0 B

.

Задача изучения механизмов зарядки водных атмосферных частиц, поставленная еще А.И. Воейковым (1904), была последовательно решена Френкелем [3]. Исходное представление состояло в том, что плотная часть двойного электрического слоя на поверхности частицы состоит из дипольных гидроксилов, ориентированных отрицательными зарядами наружу частицы, а процесс заряжения обозначался как ориентированная адсорбция ионов на атмосферных ядрах. Оценка величины поверхностного потенциала частицы Ф_s располагалась в пределах 0.25 <  ф_s <  0.36 В, причем нижняя граница соответствовала скачку потенциала на двойном слое, а верхняя — значению, вычисленному исходя из соотношения для поверхностного потенциала φ_s = n_d δp_r / ε ₀ ( n_d , δ , p_r — соответственно объемная концентрация диполей, толщина двойного слоя и проекция дипольного момента на радиальное направление сферической частицы). Таким образом, поверхностный потенциал атмосферных водных капель был принят равным φ_s = 0.3 В. Это значение и сегодня [1] считается состоятельным. Радиус частицы, несущей один элементарный заряд, по Френкелю, был равен примерно 5 нм.

Поверхностный потенциал сферической частицы, а также ее заряд и радиус связаны кулоновским соотношением φ_s = q / 4 πεε ₀ r , откуда следует равенство q = 4 πεε ₀ φ_sr . Подставляя это равенство (при е = 1) в выражение для функции f ( е ) , получаем аналогичное выражение в зависимости от радиуса частицы:

f ( r ) = e ^{2 ПЕ 0} ф 2 r / k B T

.

При этом должно выполняться условие нормировки

- 2 П£ 0 Ф 2

^kBT  d r= 1,

ю

2 πε ₀ φ_s ² _e

J kBT 0

где λ = 2 πε ₀ φ_s ² / k_BT — нормирующий множитель. Отыскание среднего (математического ожидания)

ю r = 2 j re ~ d r приводит при φs = 0.3В к противоречивому результату, т. е. к значениям среднего радиуса r = 1/ 2 = 0.827 -10—9м = 1 нм и дробного заряда q = 0.21e . Физический смысл имеет минимальный заряд частицы q = 1e и соответственно радиус частицы rmin = 4 -10-9м (4 нм). Таким образом, для интегрирования от начального значения r = rmin необходимо перенормировать функцию f (r), т. е. определить дополнительный нормирующий множитель αN из соотношения ю aN2 j е-2rd r = 1, rmin откуда следует αN = eλrmin . Вычисления дают значения αN = 126.06 и средний радиус r = = 104.25 -10-9м = 0.1мкм. При этом средний заряд частиц составит q = 22е. Ограничение области интегрирования сверху, например значением r = 1мкм , не изменяет сколько-нибудь заметно результат.

Отметим другие приближения для оценки заряда частицы, определяющие предельный заряд: рэлеевское приближение поверхностного натяжения [4]; приближение начала спонтанной автоэлектронной эмиссии в электрическом поле у поверхности заряженной частицы [4]; ударную зарядку во внешнем электрическом поле [5]; диффузионную зарядку в среде с заданной концентрацией газовых ионов [5]. Два последних механизма зарядки характерны для технологии электрофильтрации, тогда как два первых описывают фундаментальные атмосферные процессы. Наконец, ориентированная адсорбция ионов на атмосферных ядрах дает значения заряда, обоснованные выше.

Для всех пяти механизмов зарядки величина предельного заряда в функции радиуса частиц представлена в табл. 1.

Как и следовало ожидать, диффузионная зарядка и ориентированная адсорбция ионов дают наиболее близкие закономерности по величине зарядов частиц. Отметим, что диффузионная зарядка описывается кинетически, т. е. содержит множитель, зависящий от времени. Напротив, представление об ориентированной адсорбции ионов основано только на свойствах сорбирующей поверхности и потому может рассматриваться как более предпочтительное.

Вычисления механической и электрической подвижностей производились в соответствии с общим выражением k = neC_{c , m} r / 6 πrη , в котором

Табл. 1. Величина предельного заряда частицы в единицах e = 1.6·10^–19 Кл для различных механизмов зарядки

Механизм зарядки	Радиус частицы, мкм
	0.001	0.01	0.1	1.0
Рэлеевское приближение поверхностного натяжения	126	4·103	1.3·105	4·106
Приближение начала спонтанной автоэлектронной эмиссии	1	70	7·103	7·105
Ударная зарядка в земном электрическом поле E = 130 В·м–1	0	0	0	0
Диффузионная зарядка	0	1	12	125
Ориентированная адсорбция ионов на атмосферных ядрах по Френкелю	1	1–2	22	220

Табл. 2. Результаты расчетов электрической подвижности

Радиус частицы, мкм Поправки Каннингэма (Сс) или молекулярно-кинетическая (Сm) Подвижность механическая, c/кг Заряд частицы в ед. e = 1.6·10–19Кл Подвижность электрическая, см2/(В·с) 0.0005 156.275 (Сm) 0.916·1015 1 1.4662 0.001 78.137 (Сm) 0.229·1015 1 0.3664 0.002 39.068 (Сm) 0.572·1014 1 0.0916 0.004 19.534 (Сm) 0.143·1014 1 0.0229 0.006 13.023 (Сm) 0.636·1013 1 0.0102 0.01 11.787 (Сс) 0.345·1013 1–2 0.0055 0.1 1.842 (Сс) 0.540·1011 22 0.0019 1.0 1.076 (Сс) 0.315·1010 220 0.0011 5.0 1.015 (Сс) 0.595·109 1100 0.00105 зависящие от радиуса частиц поправки Каннингэма Cc или молекулярно-кинетическая Cm вычислялись по формулам [2]

C_c = 1 + ^{λ m} r

1.142 + 0.558exp

и C m = ( A + Q ) - m , r

- r

к

где λ_m — длина свободного пробега газовых молекул при нормальных условиях, λ_m = 66.5 нм; сумма A+Q= 1.175 соответствует зеркальному отражению при столкновениях молекул и частиц; кроме того, динамическая вязкость η = = 18.1 • 10 ⁶ Па-с. Результаты расчетов электрической подвижности приведены в табл. 2. и графически представлены на рис. 2.

Кнутсон и Уитби [6] описали в 1975 г. ставший основой для этих разработок электростатический

классификатор частиц по подвижности, который был предложен Чапменом [2] еще в 1937 г. Однако для преодоления технических трудностей уже в ранних вариантах таких устройств [2] требова-

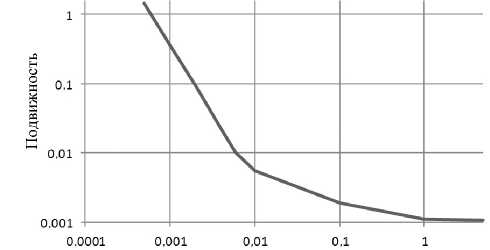
Радиус частицы, мкм

Рис. 2. Электрическая подвижность (см² / (В • с)) частиц в функции их радиуса (мкм) по данным табл. 2

лась предварительная симметричная зарядка частиц. Кроме того, необходимо было удалять из исследуемого воздуха легкие газовые ионы с подвижностью выше 1 см 2 • В ^{- 1} • с ^{- 1}, искажающие результаты измерений для относительно малоподвижных крупных частиц. Предварительная зарядка частиц при помощи β- активного ионизирующего источника или мягкого (9.5 кэВ) рентгеновского излучения используется и в настоящее время, в частности в крупных центрах по исследованию атмосферных аэрозолей [7, 8]. В этих исследованиях электростатическая сепарация частиц используется для выделения достаточно узких фракций частиц для последующего анализа другими, чаще всего оптическими методами. Предпринимались одиночные попытки обойтись без предварительной зарядки [9].

Ясно, что эти экспериментальные приемы приводили к искажению зарядовой структуры исходного аэрозоля и к обеднению спектра. Совокупность этих причин, как отмечал уже на ранних этапах исследований Фукс [2], вела к тому, что во многих работах по физике высокодисперсных аэрозолей были допущены существенные ошибки.

В этой статье показывается, что простые аспирационные приборы могут быть использованы для достаточно детального анализа спектра подвижностей атмосферных частиц. Показывается также, что инструментальная простота сопряжена с трудностями аналитического характера, которые могут быть преодолены введением некоторых вычислительных процедур.

МЕТОДИКА И РЕЗУЛЬТАТЫ

Рассмотрим цилиндрический аспирационный конденсатор, между электродами которого в осевом направлении протекает ламинарный поток анализируемого воздуха. Нетрудно показать, что для осаждения частицы (иона), имеющей начальную координату r>r 1 и подвижность k ( r ) , должно удовлетворяться неравенство

k(r). ™(r2 -r2), (1) 2t0U где r1, r2 — радиусы соответственно внутреннего (осадительного) и внешнего электродов конденсатора; t0 — время пребывания частицы в конденсаторе; U — приложенное напряжение. Для определенности предполагается, что внутренний электрод имеет положительный потенциал относительно нулевого потенциала внешнего электрода, а отрицательно заряженные частицы движутся по криволинейным траекториям к внутреннему

электроду. Распределение частиц по подвижностям характеризуется некоторой нормированной функцией f ( k ) плотности вероятности.

При определенном значении напряжения U для начальной радиальной координаты r' осаждаются ионы с подвижностью k > k ( r ') . Разобьем интервал r ₂ - r на некоторое не очень большое число одинаковых участков A r , в пределах каждого из которых будем считать координату r постоянной. Рассмотрим для определенности деление межэлектродного расстояния на 10 равных участков. Число участков принципиального значения не имеет. Очевидно, из первого участка, наиболее удаленного от осадительного электрода, осаждаются ионы с подвижностью k > k ( r '), из второго — с подвижностью k > k ( r '-A r ) , из третьего — с подвижностью k > k ( r ' - 2 A r ) и т. д. При заданном напряжении U осаждаются все ионы с подвижностью k > k ( r ') , 9/10 ионов с подвижностью k > k ( r '-A r ) , 8/10 ионов с подвижностью k > k ( r’ - 2 A r ) и т. д. Ток аспирационного конденсатора i ( U ) определяется суммарным зарядом частиц различного радиуса и заряда. Доля осаждающихся из каждого участка частиц некоторого радиуса и заряда определяется функцией плотности вероятности распределения ф ( k ) , получающейся из функции f ( k ) после умножения ее значений на коэффициенты 1; 9 /10 ; 8 / 10 и т. д. Функция плотности вероятности ф ( k ) в отличие от общей функции f ( k ) может быть названа частной. При увеличении напряжения U измеряемый ток определяется возрастающей функцией ф ( k ) . При U ^ U max этот ток определяется функцией f ( k ) . При неизменности f ( k ) этот ток есть наибольший и равный току насыщения 1 н = i ( U max ) . Приведенные рассуждения позволяют получить следующее соотношение:

к - i (U) = I>

так что

ю             ю       „2   „2

J ^{f ( k} ) ^{d k -} f ^{f ( k} ) —1 ₇d ^k

. 0                    0            ^r 2      ^r 1       ,

r ²

² r ₂

—

r ₁ ²

—

r ₁ ²

= ф ( ^k ) .

Кроме того, выполняется условие нормировки

функции f ( k ) :

to

J f ( k ) d k = 1.

При r = r₂ и соответственно при k >  k ( r ₂ ) получаем равенство ф ( k ) = f ( k ) . Из выражения (2) имеем

вольтамперная характеристика конденсатора, однако она не дает непосредственно информации о спектре подвижностей. Поскольку статистический материал (выборка) отсутствует, целесообразно сделать некоторые предположения относительно функции плотности вероятности.

В качестве наиболее общей аналитически формы распределения может быть выбрано двухпараметрическое гамма-распределение

I . - i ( U ) = k

k ( r 2 )                    to

J f ( k ) d k + J f ( k ) d k -

0                     ^k ( r , )

^{k ( r} 2 )         r 2 _ r 2          to

^- f ^f ( ^k ) —2 ---T^{d k} - f ^f ( ^k ) ^{d k}

0              ^r 2      ^r 1            k ( Г 2 )

= I h

'                     ^{k ( r} 2 )           „2 „2 '

J F [ k ( r ) ]- f f ( k ) ---- 1- d k ^J ,

L                      -r _ r ²

где F Lk (r2)] — соответствующее значение функции распределения F(k). Поскольку на основании (1) выполняется равенство r2 - r12 = k r - ri2 k ( r2 ) ■ перепишем (3) в виде

I н

- i ( U ) = I . < F L k ( r 2 ) ]_

1      ^{k ( r} 2)                 '

J ^{kf ( k} ) ^{d k} l -⁽⁴⁾

f ( k ) = ^-k^{a - 1} e^ek , (6) ^{r ( a} )

где a > 0; в > 0; k > 0 , причем форма кривой определяется параметром α , а параметр β носит характер масштабного множителя; Г ( а ) — гамма-функция Эйлера.

В зависимости от величины а функция f ( k ) видоизменяется от экспоненциального распределения ( α = 1) до почти симметричного (нормального) распределения с ростом α . Отметим, что гамма-распределение хорошо соответствует эмпирическим формулам вида f ( r ) = ar^p exp ( - br s ) , отмеченным выше. По этой причине эмпирические формулы этого вида иногда обозначают как обобщенное гамма-распределение [10].

На рис. 3 показано распределение подвижностей частиц, приблизительно соответствующее распределению частиц по размерам (рис. 1). Математическое ожидание и дисперсия подвижности даются в следующей простой форме:

Наконец, удобно ввести безразмерный ток аспирационного конденсатора

0 <

iU <  1.

I н

k=a D ( k ) ^.

Функция распределения F ( k ) дается выражением

Тогда уравнение, связывающее вольтамперную характеристику конденсатора с функцией плотности вероятности распределения подвижностей f ( k ) , запишется в виде

iU= 1 -J I .

1 ^{k (} r 2 )                  '

^{F L k ( r} 2 ^{) ]-} k ( r 2 ) J ^{kf ( k} ) ^d k p    (5)

Нетрудно показать, что соотношение (5) удовлетворяет в интервале напряжений 0 <  U <  U max обоим очевидным условиям i ( 0 ) = 0 и i ( U max ) = = I . -

Единственным источником информации при измерениях аспирационными приборами является

^F ( ^k ) = г О) ^Г 'k ( a ) ■               (7)

где Г ek ( a ) — неполная гамма-функция, определяемая интегралом

βk

Г в _к ( а ) = J t^{a - 1} e t d t . 0

Следовательно, для вольтамперной характеристики с учетом равенства (7) получаем из уравнения (5) соотношение i ( U ) = 1 - Гвк(r2 ) ( a ) + k Гвк( r2 )( ti+ 1)        (8)

I .           Г ( a )      k ( r 2 ) Г ( a + 1 ) ^{-       1} ’

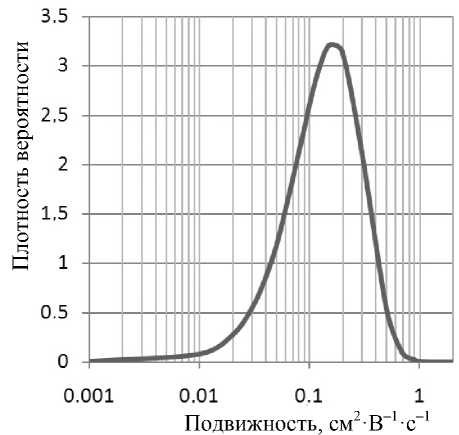
Рис. 3. Функция плотности вероятности распределения подвижностей (гамма-распределение).

f ( к ) = 864 к ²exp ( - вк ) ; a = 3; в = 12; к = 0.25; о = D= = 0.144; коэффициент вариации V 1/ V a ; коэффициент асимметрии 2/ α = 1.15 ; эксцесс 6/ α = 2; максимум (мода) при значении подвижности k = ( a - 1 ) / в = 0.167

из выражения (8), вводя аналогичные обозначения

1 - i l U maxl =6 2 ; к ( Г ) = к 0 ,

н

получаем оценку для асимптотической части характеристики:

δ 2 =

^Г вк 0 ⁽ a )   ( a / в )^г вк 0 ⁽ a + 1 )

Г( a)      к0    Г( a +1)

Таким образом, значения параметров распределения α и β могут быть получены при совместном решении уравнений системы

₆= ,   ^Г вк max ( a ) .«/в ^Г ,к „x ( a ⁺ 1 )

'         Г ( a )      к max    Г ( a + 1 )   ’

6 = ^Г вк 0 ^{( a} ) - ^a / ^{в Г} вк 0 ^{( a+} 1 )

² Г ( a )       к ₀  ’   Г ( a + 1 ) ^.

Используем теперь начальный ( U ^ 0) и асимптотический ( U ^ U max ) участки вольтамперной характеристики. При U ^ 0, т. е. при к ( r 2 ) ^ к max (для наибольшего значения подвижности; в частности, для распределения рис. 3 значения k = 2), из выражения (8) получаем

Первое из уравнений системы (12) приводится к виду (10). Вводя далее в (1) обозначение kc=     ( r22 - r12 ) In r2,

2 t ₀                 r ₁

где λ_c — коэффициент пропорциональности, зависящий только от параметров аспирационного конденсатора, получаем из (10) простое соотношение

δ 1 =

k

k max

^k λ c ^{U 1,}

i ( 0 ) ~ к = 1 a

I . ~r ( ^r 2 )    ^к ( ^r 2 ) ^в "

Введем обозначение i ( 0 ) / I_H=6 1 — произвольное, но малое значение безразмерного тока; при этом к ( r ₂ ) = к _max — наибольшее значение подвижности. Поэтому перепишем (9) в виде

в котором напряжение U ₁ соответствует принятому малому уровню безразмерного тока. Таким образом, независимо от характера функции плотности вероятности f ( к ) математическое ожидание подвижности определяется значением производной

А Г i(U)) d UI в J н

U= 0

δ= ^{1 α}

^{1 k} max ^β

то есть

.

Малая величина δ ₁ отсчитывается непосредственно по вольтамперной характеристике; соответствующее значение подвижности определяется на основании (1) при напряжении U ₁ , соответствующем уровню δ ₁ .

При U ^ U max ( i ( U ) ^ I H ) , Т. е. при ^к ( ^r 2 ) ^ ^к о

г , d fi(U) k=λcdU

I I.

U= 0

Преобразуем теперь второе уравнение в (12). Для этого запишем его в форме

2 Г( a)

Г ( a )—— Г_ю ( a + 1 ) βk ₀         βk    βk ₀

βk ₀                                βk ₀

= [ z^{a — 1} e-^z dz--— [ z^ae ^— z d z .     (15)

^Г( ^a ) о              ^ek о ^Г ( ^a ) о

Произведем оценку величины βk ₀ . Для относительно крупных частиц (малых подвижностей) величина e~^z в интегралах выражения (15) мало отличается от единицы для всех z из области интегрирования, и потому из (15) после вычислений приближенно получаем неразрешимое в элементарных функциях соотношение

₌ ( вк о ) ) Г ( а + 2 ) .

Таким образом, вообще говоря, необходимые параметры распределения α , β получаются при совместном решении уравнений (10) и (16). Трудность заключается в том, что асимптотический участок характеристики может быть сильно растянутым по причине слишком медленного роста аспирационного тока для крупных (малоподвижных) частиц. Для таких частиц ( r > >  1 мкм; к< 0.001 см²/(В • с), см. табл. 2) и при условии α >  1 величина δ ₂ становится чрезмерно малой, как это следует из анализа соотношения (16), и ее отсчет непосредственно по вольтампер-ной характеристике становится затруднительным.

Для определения параметров распределения достоверной точечной оценкой будем считать математическое ожидание подвижности, определяемое отношением k = α / β . Это значение может быть использовано для анализа распределения на основе экспериментальной вольтамперной характеристики. Для этого необходимо сначала определить значение приложенного напряжения U соответствующего осаждению на центральном электроде конденсатора всех частиц с подвижностью к ( r₂ ) = к . Далее необходимо в соответствии с (5) и при учете, как это следует из (7) и (8), записи подвижности в безразмерной форме ( вк ) получить безразмерный аспирационный ток в виде следующего соотношения:

iU = ¹ - F ( k ) ⁺ 5 “\ff ( k )^d * =

I_н                βk ₀

. ^Г , ( a ) Г . ( " + 1 ) I +

Г ( а )    Г ( ат 1 )                ⁽¹⁷⁾

Правая часть (17) является функцией только параметра распределения α , однако также неразрешима аналитически. Для оценки параметра можно воспользоваться представлением неполной гамма-функции достаточно быстро сходящимся степенным рядом. Для так называемой регуляри-зированной формы неполной гамма-функции используем ряд [11]

( х,а ) !       а^{хт 1}

_2____<_ =  X

( х, да ) !     ( х + 1 ) !

X 1

V

—

—

α x+1  α2 x+1  α3

---++

1! x+2  2! x+3  3!

где x = α ; α + 1 для расчетов соответственно второго и третьего слагаемых в правой части соотношения (17). При значении параметра α = 2 и при учете первых десяти слагаемых разложения расчет дает значение безразмерного тока, равное i ( U ) / 1 н = 1 - 0.595 + 0.233 = 0.638. Аналогично для значения а = 3 получаем i ( U ) / 1 н = 1 -– 0.998 + 0.182 = 0.184. Эта вычислительная процедура может быть организована программным путем.

ЗАКЛЮЧЕНИЕ И ВЫВОДЫ

Содержание статьи показывает, что вольтам-перная характеристика аспирационного конденсатора содержит в неявном виде материал, необходимый для анализа статистического распределения атмосферных частиц по подвижности. Отыскание параметров распределения сопряжено с некоторыми вычислительными трудностями, которые могут быть преодолены программным путем.