Спонтанное нарушение симметрии и космологическая модель с вращением для метрики типа IX по Бьянки

Спонтанное нарушение калибровочной симметрии в космологии, в том числе в космологических моделях с вращением исследовалось в ряде работ ([1, 3] и др.). Нами построена [2] замкнутая космологическая модель с вращением с метрикой вида ds2 = (dt + AC а )2 - (kC^ )2 -

• -    с ² ( (а²)² + ( а ³)² )                   ⁽¹⁾

где C = C ( t ), к , A = const ,   а ¹, а ², а³   есть

1-формы, удовлетворяющие структурным отношениям типа IX по Бьянки.

Параметры    модели:     вращение

A                  C(t)A а =-----, ускорение a =-----. При этом

2C (t)                  C (t) к мы предполагаем, что одним из источников гравитационного поля является сопутствующая идеальная жидкость.

Рассмотрим самодействующее комплексное скалярное поле p (t ) в искривленном пространстве с метрикой (1), удовлетворяющее уравнению

gik ^Sk Ф + M 2Ф -1 Rф + Л Ф*Ф2 = 0,   (2)

'63

(Л > 0), которое получается из плотности ла- гранжиана:

L = 4~g [ g'k дфдкф - M 2ф*ф +

+-ф ф--(ф ф)2],

6      6

инвариантной относительно калибровочных преобразований вида ф ^ pexp('а),  ф ^ ф exp(-'а).

Обозначим |0> гейзенберговское вакуумное состояние, определенное при t=tpl. Из пространственной однородности (1) вытекает, что если вакуумное среднее ф отлично от нуля, то оно может зависеть только от t:

< о | ф (t , x , y , z ) 10 >=< 01 ф (t ) 10 >= q( t ). (4)

Вследствие С-инвариантности состояния |0> величина q – вещественна. Отличие q от нуля означает спонтанное нарушение калибровочной симметрии. При этом в ходе усреднения (2) по состоянию |0> предполагается в древесном приближении

• <    0| /ф ²|0 >«

.       (5)

• * < 0| ф |0 >< 0| ф |0 > ² = q³

Для метрики (1): g = - C ⁶ sin x¹ к ² ,

( 12 CCk ² - 12 CCA² + 12 C ² k ² - 12 C²A² )

R = ^J------------- 272------------

2 C ² k ²

( - k ⁴ + k² A ² - 4 k ²)

2 C ² k ²

( C = C ( t )), R O

3C ( k ² - A² )

=      Ck²

Исследуем эффект спонтанного нарушения симметрии скалярного поля ^ в пространстве-времени с метрикой (1) в двух случаях:

• 1) для С ( t )= const , усредненное уравнение (2) для метрики (1) примет вид

q - a q + P q ³ = 0 ,          (6)

где

dq q = — dt

( k ⁴ - k² A² + 4 k ² -12 M² C² k ²) 12 C ² ( k ² - A ²)

• ^e = A^A• ^a >  0, ^e >  0.

При этом можно считать q =const, ввиду того, что С (t)=const.

Тогда уравнение (6) имеет два ненуле- вых решения:

q 2,3 = ±

' k ² - A ² + 4 - 12 M ² C² ,         4 C ² Л

J

при k ² - A ² + 4 - 12 M ² R ² >  0 и q_x = 0.

Предпочтительность выбора решений q 2,3 ^ 0 из соображений минимума энергии дает возможность выявить спонтанное нарушение калибровочной симметрии. В этом случае несимметричное вакуумное состояние |0> энергетически более выгодно, чем симметричный вакуум. Используем метрический тензор энергии – импульса для скалярного поля ф :

TV = vфгф+vVv^Ф-§v\va^vj-

-M2ф* ф]-1[-R^ +1 §1R + VVvА -       (8) -8V О]0ф+Л sv (фф2.

где R ^ - тензор Риччи, § ^ - единичный тензор.

Вакуумная плотность энергии для данной модели равна

Е=<о | т^о о | о> =1 M ² +¹ R ¹ -¹ R I q ² +

• <      3     6 J

+^Л q ⁴.                  (9)

Подставляем решения уравнения (6) в (9) и находим:

E(q1) = 0, w _ (k2 - A2 + 4 -12M2C2)2 n /1ЛЧ E(q2;3)---4------------< 0 . (10)

96 C ⁴ Л

Мы рассматриваем космологическую модель, где R и M – постоянные, за счет варьирования параметров источников гравитационного поля можно менять A и k , тогда эффект спонтанного нарушения симметрии будет     при     выполнении     условия

12 M ² C ² <  k ² - A ² + 4 .

Таким образом, энергетически более выгодным будет несимметричное вакуумное состояние | 0> (q ^ 0), что означает спонтанное нарушение симметрии вакуума.

• 2)    для R (t)=vt , M =0, уравнение (2), усредненное по гейзенберговскому вакуумному состоянию с учетом древесного приближения имеет вид:

  q ⁺ q^q

  
  

  —

  
  

  ( k ⁴ - k² A ² + 4 k²

  
  

  —

  
  

12 v ² ₍ k ² - A ²)

+ ТГ—n Л q ³ = 0. 3 ( k ² - A ²)

f ( t )

Сделав замену q =----, получим ft2 + ft -

k ⁴ - k² A ² + 4 k² 12 v ²( k ² - A ²)

f +

k ²

+ 3 ₍ k ² - A ²)

Л f ³ = 0,

сделаем замену Т = ln t, получим k4 - k2A2 + 4k2 12v2 (k2 - A2)

q +

k ²

+ 3 ₍ k ² - A ²)

Л f ³ = 0,

df

где f=A dr

Уравнение Дюффинга (13) имеет два устой-

чивых решения и одно неустойчивое:

f = о, f ₃=±_A E- Z H⁴ . ±, ^{1         ,3} v Л 2 v

k ² - Z + 4 >  0, Л> 0.

В качестве начальных условий для решения (13) возьмем:

\   । k^ — Z + 4 i

f(t pi ) = ±д       7       ’ 7“, f (t pi ) = ^0.

V Л     2 v

Уравнение (13) имеет ненулевое решение, соответствующее перестройке вакуума в состояние с нарушенной калибровочной симметрией.

Тогда решения уравнения (11):

космологическая модель с вращением для метрики Ожвата–Шюкинга вида:

ds2 =(dt)2+R 1-2k2w3dt-

I у I *((1-k)(w¹)²+(1 + k)(w²)² +   (17)

+(1+2k2)(w3)2), w1 = cosx3dx1 +sinx1sinx3dx2, где w2 = -sinx 3dx1 +sinx1cosx3dx2, w3 = cosx1dx2 +dx3.

0 < x ¹<  n ,  0 < x ², x ³<  2 n ,

R , k = const ,  | k | <  Z.

q i = 0, q 2,3 = ±

k^{2 Z + 4} • — . (15)

Л      2 vt

Обсудим теперь вопрос о предпочтительности вакуумного состояния |0> с энергетической точки зрении. Подставим (15) в выражение (9) и, учитывая также, что R ( t )= vt , M =0, получим:

E(q 1 ) = 0,

( 48 v ² ( k ² - Z ) - k ⁴)( k ² - Z + 4 )

E(q 2;3 )=              ^{8 t4} v⁴ k ^{2 Л}                (16)

( k²Z - 4 k ²)( k ² - Z + 4 )

⁺          8 t⁴ v⁴ k² Л          ’

Отметим, что в работе [4] получена космологическая модель с вращением с метрикой (17), заполненная пылью, с космологическим членом. Источником гравитационного поля нашей космологической модели является

несопутствующая идеальная жидкость с тензором энергии-импульса T_mn=(e+p)u_mu_n-pg_mn , где

£ >  0, U ^ U ^A = 1 .

Компоненты вектора скорости рассмот-

рим в следующем виде:

u _o ^ 0 , U = 0 , u₂ = U2^1-2^cosx¹ , u ₃ =u ₃ 1-2k² .

При выполнении условия

v

<

k ⁴ - k Z ² + 4 k²

48 ( k ² - Z )

, k ² >  Z

вакуумная плотность энергии E(q 2;3 ) отрица-

У нас эйнштейновская гравитационная постоянная равна 1.

Тогда ненулевые уравнения Эйнштейна для метрики (17) запишутся в следующем ви-

де:

тельна.

Таким образом, так же, как и в предыдущем случае, энергетически более выгодным будет несимметричное вакуумное состояние |0>, и ненулевые решения (15) уравнения (11) соответствуют перестройке вакуума в состояние с нарушенной калибровочной симметрией.

8k² -5 (k²-1)R 8k² -1

₂= (e+ p)u₀² - p ,

2R(k2 -1) 8k2 -1

2R(k2 -1)

R =(e+ p)u0u2- p ,

R

= (e+ p)u0u3- p ,

Модель с метрикой Ожвата– Шюкинга

В настоящее время не теряет своей актуальности вопрос о возможном вращении Вселенной и его связи с вращением галактик. Поэтому сохраняется интерес к построению и исследованию космологических моделей с вращением. Нами построена стационарная

1 (k2-1)

= pR2,

-

(k2-1)

- (16 k ⁴ - 2 k ² -1) _ 4( k ² -1)    "

= -pR2,

,                   2л R ²(1 + 2 k ²)

= ( £ + p ) u₂u ₃ (1 - 2 k ) + p-----------

- (16 k ⁴ - 2 k ² -1) _

4( k ² -1)     "

/        2/,    .,2a      R ²(1 + 2 k ²)

- (s + p) u3 (1 - 2 k ) + p----“---- cos2(x3) sin2(x1)k

4( k ² - 1)

sin² ( x ¹ )(16 k ⁴ - 2 k ²) - 16 k ⁴ + 2 k ² +1 _

4( k ² - 1)              ”

- ( s + p ) и 2 (1 - 2 k ²) cos² ( x ¹) +

R ² (1 + k sin² ( x ¹) cos 2( x ³) + 2 k ² cos² ( x ¹)) ^p 4 ^.

Из уравнений (19), (20) вытекает, что u2 — и3, тогда уравнения (23) и (24) будут одинаковы.

Из уравнений (21),  (22) получаем p=         . Подставим p в уравнения (18),

(19), (23) и (25), и получим следующую систему уравнений:

( s + p ) и 02 —	8 k 2 - 4	(26)
	R 2( k 2 -1) ,
( s + p ) и 0 W 2	4 k 2	(27)
	— R ( k 2 -1) ,
~ 2	- 4 k4	(28)
( s + p ) и 2 — у 2 ( k	- 1)(1 - 2 k 2) .

Из условия и _и и ^и — 1 получим уравнение

₂(2 k ² + 1)   ,  _ (1 - 2 k ²)

^и 0     +     u ^{2 и} 0 ^и 2

- о и ,^ — 1.

² R ²

Решая систему уравнений (26), (27), (28) при условии (29) находим, что

8 k ² - 3      ₂   2(2 k ² -1)

s —  -—5----, и ₀ —----------,

R ²( k ⁰ - 1)     ⁰    4 k ⁰ - 1

2         2k⁴ R ²

^{и 2 —} (2 k ² -1)(4 k ² -1)'

Условия S > 0, и0 > 0, и2 > 0 выполняют ся при |k| < ^ . Для данной модели расшире- ние, сдвиг и ускорение отсутствуют, вращение модели отлично от нуля при Ы0:

2 2 k ²

^—  R 4 1 - 4 k ² 71 - k² ’

Применяя метод, предложенный в [5], найдем условия, которые обеспечивают причинность пространства-времени с метрикой (17).

Пусть X и (S) - произвольная времениподобная кривая (s - параметр), v^v^ > 0. Если предположить, что эта кривая – замкнутая, тогда всегда существует такое S — So, при котором производная

dt-     — 0 .

^ds S — S ₀

Вычислим в точке S — So квадрат мо- и dx*                        х дуля Vи —---, касательного к X^ (S)

ds

(

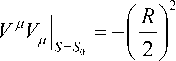
(1 -k) Т + ds к       v 7

(г ? ₇ ⁰

+(1+k) — кds 7

3? 7 + (1 + 2 k ²) — I ds ) ^{4    7} 7

.

При k <  1 в точке S — S_o имеем:

V UV    < 0 .Но мы предположили, что и 1S—S 0

X ^и ( S )     - времениподобная кривая

( V ^U VJ    >  0 ) при любых S .

^и S — S 0

Таким образом, мы получили противоречие с исходным предположением о замкнутости X ^и ( S ) . Значит, условие, накладываемое на наше решение | k | < — , обеспечивает отсутствие замкнутых времениподобных кривых во всем пространстве – времени с метрикой (17).

Полагаем, нашу модель с метрикой (17) можно использовать для исследования космологических эффектов, обусловленных только вращением Вселенной.

Сделаем оценку космологического вращения для нашей метрики.

Пусть р - плотность материи в этой модели и р - 10 ^{- 30} г / см ³.

Тогда для нашей модели можно получить, что скорость вращения будет — - 10 ^{- 13} рад/год при k - 10 - 2 , что совпадает с результатом Берча.