Сравнение потранзисторного резервирования с троированием логических элементов

Как показано в [1–4] резервирование путем учетверения–расчетверения КМДП-транзисторов в ряде случаев позволяет даже выиграть в сложности по сравнению с троированной (мажоритированной) схемой – при определенном соотношении сложности исходной схемы и сложности мажоритарного (мажоритарных) элементов. При этом достигается значительный выигрыш в вероятности безотказной работы по сравнению с мажоритировани-ем, конечно, за счет снижения быстродействия.

Вызывает интерес сравнение такого резервирования с троированием элементов. Исследуем резервирование на примере полного сумматора, содержащего схему сложения по модулю 2 трех переменных (исключающее ИЛИ 3XOR) и схему переноса – мажоритарный элемент.

1.    Резервирование функции переноса на уровне транзисторов

Элемент, реализующий функцию бинарного переноса (мажоритарный элемент) с парафазным выходом при наличии парафаз- ных входов переменных A, NA, B, NB, C, NC [5], с формированием парафазных выходов Р, NР в упрощенном виде показан на рис. 1:

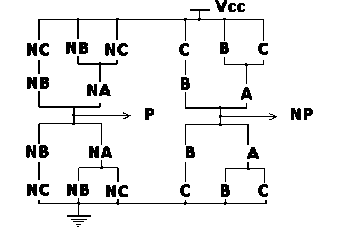
Рис. 1. Реализация функции бинарного переноса – мажоритарной функции

Элемент (рис. 1) реализует парафазную функцию переноса:

P(A, B, C, NA, NB, NC) = NB ⋅ NC ∨ NA ⋅

⋅ (NC ∨ NB),                              (1)

NP(A, B, C, NA, NB, NC) = B ⋅ C ∨ A ⋅ (C ∨ B)

Предлагается резервирование путем расчетве-рения (или учетверения) на уровне каждого из КМДП-транзисторов. Так, схема подключения + питания (Vcc) будет выглядеть следующим образом (рис. 2):

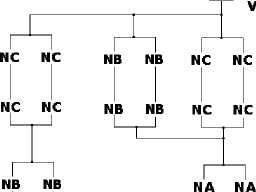
2. Оценка вероятности безотказной работы резервирования на уровне КМДП-транзисторов функции бинарного переноса

к схеме подключения "О вольт”

Рис. 2. Потранзисторное резервирование схемы подключения + питания (Vcc) функции (1)

Покажем, что такое резервирование на уровне одного элемента позволяет получить большую вероятность безотказной работы, чем троирование, при тех же затратах в транзисторах.

Для транзисторной реализации сумматора при экспоненциальной модели отказов имеем:

P₁ = e -(20) λ ⋅ t

.

Легко видеть, что отказ одного любого транзистора в каждой четверке КМДП-транзисторов не изменит значение логической функции, например NC:

NC ⋅ NC ∨ NC ⋅ NC = NC. (3)

Аналогичный (рис. 2) вид имеет и функция подключения шины «0» вольт. Так же резервируется функция (2). Все это возможно тогда и только тогда, когда в исходной схеме последовательно соединяются всего два транзистора, поэтому получим в предлагаемой схеме четыре транзистора, что соответствует ограничениям Мида и Конвей [6].

Для резервирования источника питания может быть предложен вариант (рис. 3):

Если резервировать каждый из 20 тран-

зисторов, то

P(t) fct2 = [e ^{- 4 ⋅ λ ⋅ t} + 4 ⋅ e ^{- 3 ⋅ λ ⋅ t}(1 - e ^{- λ ⋅ t})]²⁰.              (5)

При троировании с одним мажоритаром по каждому из двух выходов (для мажорити-рования будем использовать те же схемы реализации функции переноса) имеем:

P₃ = (3 ⋅ e -2 ⋅ (20) ⋅ λ ⋅ t -2 ⋅ e -3 ⋅ (20) ⋅ λ ⋅ t ) ⋅ e -20 ⋅ λ ⋅ t .             (6)

Если троировать мажоритары по выхо-

дам, то получим

P_3.3 = (3 ⋅ e -2 ⋅ (20) ⋅ λ ⋅ t -2 ⋅ e -3 ⋅ (20) ⋅ λ ⋅ t ) ⋅

⋅ (3 ⋅ e -2 ⋅ (10) ⋅ λ ⋅ t - 2 ⋅ e -3 ⋅ (10) ⋅ λ ⋅ t ) 2 .

Графики сравнения вариантов выражений (4)–(7) отказоустойчивой реализации функции переноса изображены на рис. 4, 5.

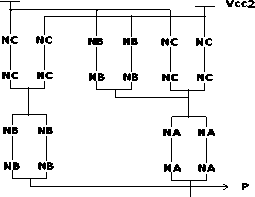
к схеме подключения "О вольт"

Рис. 3 . Вариант резервирования источника питания

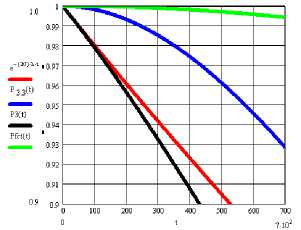
Рис. 4. Графики сравнения вариантов – выражения (4)–(7) отказоустойчивой реализации функции переноса, λ = 10^-5 1/час

Получаем затраты 4*20=80 транзисторов, максимальный путь от шин на выход (быстродействие) =4 транзистора.

При троировании схемы реализации переноса с двумя выходными мажоритарами (для выходов Р, NР) получаем такие же затраты: 3*20+20 =80 транзисторов, путь такой же – 4 транзистора. При троировании выходных мажоритаров получим: 3*20+3*20 =120 транзисторов.

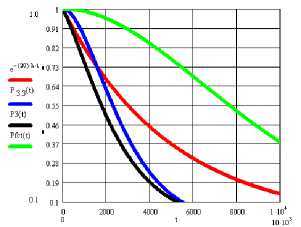
Рис. 5. Графики сравнения вариантов – выражения (4)–(7) отказоустойчивой реализации функции переноса до вероятности 0,1; λ = 10^-5 1/час

Таким образом, потранзисторное резервирование дает существенный выигрыш в вероятности безотказной работы, причем быстродействие не уменьшается, в то время как простое троирование оказывается менее эффективным, чем нерезервированная схема, и попросту нецелесообразно. Троирование с тремя мажоритарами при увеличенных на 40 % затратах (120 против 80 транзисторов) дает меньшее приращение вероятности безотказной работы. При достижении определенного времени такое резервирование также становится нецелесообразным.

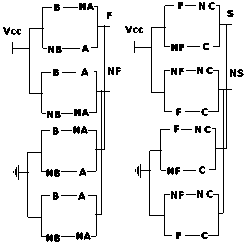
Рис. 7 . Транзисторная реализация двух па-рафазных функций исключающего ИЛИ двух парафазных переменных A, NA, B, NB;

F, NF, C, NC (см. формулы 10, 11)

3 . Резервирование сложенияпо модулю 2 на уровне транзисторов

Транзисторная реализация парафазной бинарной суммы по модулю 2 S, NS [5] при наличии парафазных входов переменных A, NA, B, NB, C, NC представляет собой (рис. 6).

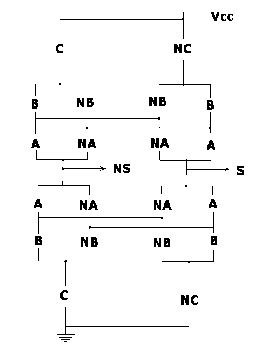
Рис. 6. Транзисторная реализация пара-фазной функции исключающего ИЛИ трех парафазных переменных A, NA, B, NB, C, NC (см. формулы 8, 9)

S(A, B, C, NA, NB, NC) =

= NA ⋅ NB ⋅ NC ∨ NA ⋅ B ⋅ C ∨ A ⋅ NB ⋅ C ∨ A ⋅ B ⋅ NC,

NS(A, B, C, NA, NB, NC) =

• =    NA ⋅ NB ⋅ C ∨ NA ⋅ B ⋅ NC ∨ A ⋅ B ⋅ C ∨ A ⋅ NB ⋅

Можно увидеть, что в схеме имеется 3 КМДП-транзистора подряд, т. е. при резервировании получатся цепочки из 6 транзисторов подряд, что недопустимо [6].

Поэтому придется переходить от одной функции 3XOR к двум функциям 2XOR – т. е. выполнить декомпозицию на схемы, в которых имеется не более двух последовательно включенных транзисторов (рис. 7):

S(A, B, F, NA, NB, NF) =

• =    NA ⋅ NB ⋅ NF ∨ NA ⋅ B ⋅ F ∨ A ⋅ NB ⋅ F ∨ A ⋅ B ⋅ NF,

NS(A, B, F, NA, NB, NF) =

• =    NA ⋅ NB ⋅ F ∨ NA ⋅ B ⋅ NF ∨ A ⋅ B ⋅ F ∨ A ⋅ NB ⋅ NCF.

Таким образом, аппаратные затраты увеличиваются: было 20 транзисторов, стало 32, быстродействие снизилось: был путь 3, стал 4.

Итак, при потранзистроном резервировании получаем 32*4=168 транзистора, путь увеличивается более чем в 2 раза – 8.

Отметим, что при мажоритировании нет необходимости в декомпозиции: получаем аппаратные затраты 3*20=60, плюс два мажо-ритара по каждому выходу S, NS сложностью 10 транзисторов, итого 80. Путь 5.

Если использовать три мажоритара, получаем сложность 3*20+3*20=60+60=120, путь тот же – 5.

Сравним варианты реализации суммы по модулю 2 трех переменных без резервирования -e^{-24 λ t} , резервирования с тремя мажори-тарами ( P_3.3 ), резервирования с одним мажо-ритаром ( P₃ ), учетверение ( P_fct ) (рис. 8, 9).

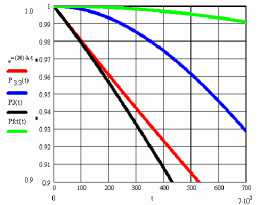
Рис. 8. Графики сравнения вариантов без резервирования - e^{-20 λ t} , резервирования с тремя мажоритарами ( P_3.3 ), резервирования с одним мажоритаром ( P₃ ), учетверение ( P_fct ) отказоустойчивой реализации сумматора, λ = 10^-5 1/час

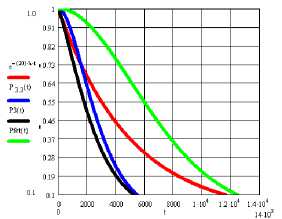
Рис. 9. Графики сравнения вариантов без резервирования - e^{-24 λ t} , резервирования с тремя мажоритарами ( P_3.3 ), резервирования с одним мажоритаром ( P₃ ), учетверение ( P_fct ) отказоустойчивой реализации сумматора в диапазоне до вероятности 0,1; λ = 10^-5 1/час

Выводы

Таким образом, резервирование по каждому КМДП-транзистору раздельное, потран-зисторное резервирование, или расчетверение выглядит предпочтительнее по вероятности безотказной работы даже троированной схемы с троированием мажоритаров. Простое троирование (с одним мажоритаром) оказывается менее эффективным, чем нерезервированная схема и не имеет смысла на уровне сумматора. В то же время при потранзистор-ном резервировании допустимо большее количество отказов – один в каждой "четверке" транзисторов против одного отказа в одном из четырех экземпляров схемы. Но раздельное потранзисторное резервирование требует большего количества связей, при этом желательно расчетверение входов элемента.

В любом случае, быстродействие снижается – путь от шин питания увеличивается в 2 раза. При резервировании цепочек транзисторов длиной более двух необходимо выполнять декомпозицию (в связи с ограничением в КМДП-схемах, запрещающем использование последовательного соединения более чем четырех транзисторов). При этом сложность реализации значительно возрастает, а задержка увеличивается более чем в 2 раза.