Сравнительный анализ эффективности проекционного метода нелокального улучшения управления

Приближенные методы решения задач оптимального управления продолжают развиваться по разным направлениям в работах многих исследователей (A.B. Аргучинцев, A.C. Булдаев, В.И. Гурман, В.А. Дыхта, В.И. Зубов, В.Б. Колмановский, В.Ф. Кротов, В.А. Срочко, А.И. Тятюшкин, Р.П. Федоренко, Ф.Л. Черноусько и другие). В частности, В. Ф. Кротов в работе [9] описал общий метод глобального улучшения управлений, близкий к так называемым нелокальным методам улучшения в дифференциальных системах, разрабатываемых в работах В. А. Срочко и А. С. Булдаева [2, 3, 4, 7].

Методы нелокального улучшения в отличие от локальных методов (например, метода условного градиента) не рассматривают операции слабого или игольчатого варьирования управления на каждой итерации с параметрическим поиском (который является довольно трудоемким) в достаточно малой окрестности улучшения. Основой методов нелокального улучшения в различных классах задач оптимального управления являются формулы приращения целевых функционалов без остаточных членов разложения. В результате последовательного решения задач улучшения управления генерируется релаксационная последовательность управлений, обладающая возможным свойством улучшать неоптимальные управления, удовлетворяющие принципу максимума, включая особые управления.

В статье проводится сравнительный анализ эффективности проекционного метода нелокального улучшения на тестовых задачах.

• 1.    Постановка задачи

Рассматривается следующий класс задач оптимального управления:

x (t ) = f (x (t), u (t), t), x (t0 ) = x 0, u (t)g U, t g T = [t0,ti], t1

Ф(u) = ф(x(t)) +jF(x(t), u (t), t) dt ^ inf,(3)

t 0

где x ( t ) g R" - вектор состояния, u ( t ) g R^r - вектор управления. В качестве допустимых управлений рассматривается множество V кусочно-непрерывных на [ 1 ₀, t 1 ] функций со значениями в выпуклом компактном множестве U с R^r . Промежуток управления - [ 1 ₀, t 1 ] и начальное состояние x ₀ заданы. Задача (1) - (3) является задачей оптимального управления со свободным правым концом.

Предполагаются выполненными следующие условия:

• 1)    функция ф ( x ) непрерывно-дифференцируема на R ” , вектор-функция F ( x , u , t ) , f ( x , u , t ) и их производные F_x ( x , u , t ) , F_u ( x , u , t ) , f_x ( x , u , t ) , f u ( x , u , t ) непрерывны по совокупности аргументов ( x , u , t ) на множестве R ” x U x T ;

• 2)    функция f ( x , u , t ) удовлетворяет условию Липшица по x в

Rⁿ х U х T с константой L >  0

|| ^f ( x , u , t ) - f ( y , u , t )|| < Lx ^- y ||.

Эти условия гарантируют существование и единственность решения x ( t , v ) , t e [ t ₀, t 1 ] системы (1) - (2) для любого допустимого управления v ( t ) , t ^e [ t o , t i ] .

Решать поставленную задачу (1) - (3) будем при помощи модифицированного проекционного метода нелокального улучшения управлений с дифференциально-алгебраической сопряженной системой [2, 3, 4].

Сначала рассмотрим саму дифференциально-алгебраическую сопряженную систему [3, 4]:

p (t ) = -Hx (Р (t),x0 (t), u0 (t), t)-r (t), p (t1 ) = -Фx (x0 (t1))- q,

H ( p ( t ) , x ( t ) , u ⁰ ( t ) , t ) - H ( p ( t ) , x ⁰ ( t ) , u ⁰ ( t ) , t ) =

H Hx (p (t), x0 (t), u0 (t), t) + r (t), Ax (t )) ,(6)

ф( x (t1))-ф( x0 (t )) = ^p( (x0 (t1))+q,Ax (t1)}, где H (p, x, u, t ) = pp, f (x, u, t )^-F (x, u, t) - хорошо известная функция Понтрягина, Hx (p, x, u, t), фx (x (t1)) - производные соответствующих функций по x. u0 (t) e V - допустимое начальное значение управление, x0 (t) - решение уравнения (1) для этого начального управления, Ax (t) = x (t1) - x0 (t1).

Величины r ( t ) и q всегда можно выразить из соответствующих алгебраических уравнений (6) и (7) (возможно и не единственным образом) [3, 4] и, таким образом, система (4) - (5) всегда может быть сведена к вспомогательной дифференциальной сопряженной системе.

Следует заметить, что если в задаче (1) - (3) f , F линейны по x , то из [3, 4] следует, что r ( t ) = 0 , а если ф линейна, то q = 0 . В нелинейном случае, если в некоторый момент времени t e T x ⁰ ( t ) = x ( t ) , то полагаем r ( t ) = 0 . Если при этом t = t 1 , то q = 0 .

Далее для допустимого управления u е V и фиксированного параметра a >  0 рассмотрим проекционное отображение:

u a ( p , x , t ) = P u ( u ( t ) + a H_u ( p , x , u , t ) ) , t g [ t 0 , t 1 ] , где P U - оператор проектирования на множество U в евклидовой норме, H u ( p , x , u , t ) - производная функции Понтрягина по управлению.

Дифференциальный принцип максимума (ДПМ) в задаче (1) - (3) для управления u е V с помощью отображения u a представляется в виде:

u ( t ) = u ^a ( p ( t , u , v ) , x ( t , u ) , t ) , t g [ t 0 , t 1 ] ,                  (8)

где p ( t , u , v ) - сопряженная переменная. Для выполнения ДПМ достаточно проверить условие (8) хотя бы для одного a >  0.

Для заданных a > 0 и u0 е V определим отображение wa с помощью соотношения wa (p,x,t,5) = Pu (u0 (t) + a(Hu (p,x,u0 (t),t) + 5(t))), t g[t0,ti] .

Параметр проектирования a >  0 рассматривается в качестве параметра возмущения . Уравнение (1) в данном случае примет вид:

x (t ) = f (x)(x (t), wa (p (t) , x (t), t, 5 (t)), t), x (10 ) = x0. (9) Итерационный процесс при фиксированном a > 0 и заданном u0 е V имеет вид uk+1 (t) = Pu (u0 (t) + aHu (pk (t),xk (t),uk,t) + 5(t)), t е [10,ti], где на начальной итерации (нулевой итерации) задается начальное приближение u0 е V. 5 (t) определяется из уравнения

H ( p ( t , u ⁰, u^k ) , x ( t , u^k ) , u^k ( t ) , t ) -

- H ( p ( t , u ⁰, u^k ) , x ( t , u^k ) , u ⁰ ( t ) , t ) =

HH_u ( p ( t , u ⁰, u^k ) , x ( t , u^k ) , u ⁰ ( t ) , t ) + 5 ( t ) , u^k ( t ) - u ⁰ ( t )^, (10) x^k ( t ) , p^k ( t ) являются решениями системы (9) и дифференциальноалгебраической сопряженной системы (4) - (7) на k итерации, соответственно. В случае линейной по управлению задаче (1) - (3) 5 ( t ) = 0 , t е T . [3, 4].

Вычисляя 5 ( t ) , r ( t ) и q мы можем применить некоторые условия [5, 6]. Сначала опишем условия для нахождения 5 ( t ) :

• 1.    Если все компоненты u k ( t ) = u ⁰ ( t ) , то алгебраическое уравнение (10) выполняется тождественно. В этом случае компоненты 5 ( t ) могут принимать произвольное значение, тогда, выбираем значения всех компонент 5 ( t ) , исходя из непрерывности, т.е. полагая равным значению 5 ( t ) в соседнем левом узле. При этом, если t = t ₀ (начальный момент), то слева нет узла, а значит, выбираем любое значение, например 5 ( t ₀ ) = 0 , для всех компонентов;

• 2.    Если, хотя бы одна компонента вектора u k ( t ) * u ⁰ ( t ) , то именно для этой компоненты однозначно определяется соответствующая компонента 5 ( t ) из формулы (10), один из вариантов такого

определения:

Az HI ( p , X , u , t )       z . X Z X X

S_k ( t ) =——-----TT-- H^p^t , u °, u^k ), x^t , u^k ), u ⁰ ( t ) , t^ ,

A uk (t)           v x x                / где Au(t)H(p, x, u, t) = H(p (t, u0, uk), x(t, uk), uk (t), t)-

H(p(t,u0,uk),x(t,uk),u0 (t),t) и Auk (t) = uk (t)-u0 (t). Причем все остальные компоненты нужно положить равными по непрерывности значениям в левом соседнем узле. Но если при этом t = 10, то полагаем, что эти остальные элементы равны нулю.

Теперь покажем условия для определения r (t) и q. Но для начала перепишем дифференциально-алгебраическую сопряженную систему (4) - (7) в итерационном виде:

pk+1 (t) = -Hx (pk+1 (t),x0 (t),u0 (t),t)-r(t),(11)

pk+1 (t ) = -Фх (x 0 (t1))- q,

H ( p^k ( t ) , x^k ( t ) , u ⁰ ( t ) , t ) - H ( p^k ( t ) , x ⁰ ( t ) , u ⁰ ( t ) , t ) =

H Hx (pk (t), x0 (t), u0 (t), t) + r (t), xk (t)- x0 (t )^,(13)

^(xk (t1))-^(x0 (t1 )) = (^x(x0(t1))+q,xk (t1)-x0 (t1)). (14)

где p^k ( t ) = p ( t , u ⁰, u^k ) , x^k ( t ) = x ( t , u^k )

Таким образом, вычисляя

r (t) и q из уравнений (11) - (14) необходимо учитывать следующие условия:

• 1.    Если все компоненты x^k ( t ) = x ⁰ ( t ) , то алгебраическое уравнение (13) выполняется тождественно. В этом случае компоненты r ( t ) могут принимать произвольное значение, тогда, выбираем значения всех компонент r ( t ) , исходя из непрерывности, т.е. полагая равным значению в соседнем правом узле. При этом, если t = t 1 (конечный момент), то справа нет узла, следовательно, выбираем любое значение, например r ( t 1 ) = 0 для всех компонентов. Также если в этот конечный момент выполняется x^k ( t 1 ) = x ⁰ ( t 1 ) уравнение (14) обращается в тождество, поэтому задаем, например, q = 0 для всех компонентов;

• 2.    Если, хотя бы одна компонента вектора x^k ( t ) ^ x ⁰ ( t ) , соответствующая компонента r ( t ) однозначно определяется именно для этой компоненты из формулы (13), один из вариантов определения:

• 2.    Вычислительный эксперимент

Az HI ( p, X, U, t)        z . X Z X X rk (t)=       a --Hx (p(t,u°,uk ),x(t,uk ),u0 (t),t),

Axk (t)              x v x ’           ’

где                              A _{x ( t} ) H ( p , x , u , t ) = H ( p^k ( t ) , x^k ( t ) , u ⁰ ( t ) , t ) -

H ( p^k ( t ) , x ⁰ ( t ) , u ⁰ ( t ) , t ) и A x_k ( t ) = x^k ( t ) - x ⁰ ( t ) . Причем все остальные компоненты нужно положить равными по непрерывности значениям в правом соседнем узле. Но если при этом t = t , , то полагаем, что эти остальные компоненты равны нулю. Аналогичное, соответствует для q из уравнения (14).

Для сравнительного анализа рассматриваемого метода проведем вычислительный эксперимент. Вначале опишем общие параметры.

Вычисленные значения управляемых, фазовых и сопряженных переменных будем запоминать в узлах равномерной сетки с шагом дискретизации At = 10-3 на отрезке [10, t1 ]. В промежутках между соседними узлами сетки значение управления принимаем постоянным и равным значению управления в левом узле. Численный расчет задачи проводим до первого улучшения. Далее строим новую задачу, и повторяем итерационный алгоритм. В качестве критерия остановки выбираем условие

ф(uk+1 )-Ф(uk) - ф(uk ) 'е, где ^ > 0 - заданная точность (в примере е = 10-4). Эффективность методов также зависит и от алгоритмов, используемых для решения вспомогательных задач, например, интегрирование дифференциальных систем. По этой причине, численное решение фазовых и сопряженных задач Коши будем осуществлять методом Рунге-Кутта-Вернера пятого или шестого порядка точности с помощью библиотеки IMSL языка Fortran PowerStation 4.0 [1]. При вычислении 5 (t), r (t) и q принимаем условия, описанные выше, только внеся некоторое изменение: мы фиксируем один из r (t) равным нулю и проводим дальнейшее вычисление по обычным правилам. В качестве результата выбираем наилучшее решение

Пример 1. Оптимальная ориентация летательного аппарата в пространстве [8] .

• ^x 1 ( t ) = ^x 3 , <  x 2 ( t ) = X 4 , x ₃ ( t ) = - x 4 + u 1 sin u 2 x ₄ ( t ) = x 3 + u 1 cos u ₂

x1 (0) = 10, x2 (0) = 0, x3 (0) = 10, x4 (0) = 0, t e[0, t1 ].

Ф ( u ) = t 1 + 1000 ^ x f ( t 1 ) ^ min.

i = 1

Проведем расчет с помощью проекционного метода нелокального улучшения и сравним с результатами, полученными в [8]. Для решения задачи введем необходимые конструкции.

Функция Понтрягина для заданной задачи записывается следующим образом:

H ( p , x , u , t ) = p 1 x ₃ + p ₂ x ₄ +

+ p ₃ ( u 1 sin u ₂ - x ₄ ) + p ₄ ( x ₃ + u 1 cos u ₂ ) .

Градиенты:

H x , = ⁰ , ^H x 2 = ⁰, ^H x 3 = p 1 ⁺ p 4 , ^H x 4 = p 2 ^- p 3 ,

H u = p ₃ sin u ₂ + p ₄ cos u ₂ , H u = p ₃ u 1 cos u ₂ - p ₄ u 1 sin u ₂ .

Дифференциально-алгебраическая сопряженная система запишется в следующем виде:

p1 (t) = 0, p1 (t1) = -2000x1 (t1)- q1, p2 ( t) = 0, P2 ( t1 ) = -2000x2 ( t1 ) - q2, p3 ( t ) = -P1 - P4 , P3 ( t1 ) = -2000x3 ( t1 ) - q3, p3 ( t ) = — P2 + P3 , P3 ( t1 ) = -2000x3 ( t1 ) - q4.

В исходной задаче f , F линейны по x , значит r ( t ) = 0 , г = 1,4 . Для нахождения q используем формулу:

^W^ x lM  ₀

qk ' t)        xk (t,)-x0 (t,)        9x (x ' t1'),

полученную из (14),   вместе с правилами описанными выше.

Итерационный процесс при фиксированном a >  0 и заданном и ⁰ е V

U+1 (t) = Pu (и0 (t)+ aHu (P (t),xk (t),uk,t)+x(t)), t e[ t 0, t1 ] , где x (t) находится по правилу выше. В качестве начального приближения выбиралось управление и0 (t) = 0.

В таблице 1 приводятся результаты, полученные рассматриваемым методом (ПМНУ) и методами из работы [8] ( Ф * обозначает наилучшее значение функционала).

Таблица 1. Сравнительный анализ эффективности

Метод	Ф	Кол-во задач Коши
1	10.285456	47422
2	10.288656	100048
ПМНУ	10.290443	33907

Проекционный метод для данной задачи показал меньшую трудоемкость по количеству решенных задач Коши, хотя и уступил по точности решения. На следующих рисунках представлен рассчитанный оптимальный процесс (итоговые управление и фазовые траектории):

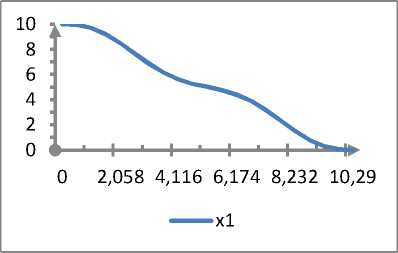
Рисунок 1. Фазовая траектория х 1 ( t )

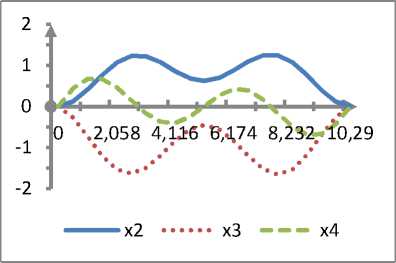
Рисунок 2 . Фазовая траектория x 2 ( t ) , x 3 ( t ) , x 4 ( t )

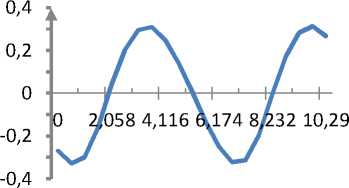
Рисунок 3. Управление u 2 ( t )

Итоговое управление u 1 ( t ) = 1 , t e [0, t 1 ] не представлено.

Пример 2. Оптимальное управление потоком хладагента в химическом реакторе [10, с. 405 - 407]

Рассматривается задача стабилизации химического реактора, представляющая собой аппарат с мешалкой и подведенным каналом поступления хладагента:

Ф( u )= J (x2 (t) + x 22 (t)) dt ^ inf, 0

x ( t ) = - 2 ( x 1 + 0.25 ) + ( x ₂ + 0.5 ) e^² - ( x 1 + 0.25 ) u , x 1 ( 0 ) = 0.05 , x ₂ ( t ) = 0.5 - x ₂ - ( x ₂ + 0.5 ) ee^ x , x ₂ ( 0 ) = 0 , x 1 ( 0.78 ) = 0 , x ₂ ( 0.78 ) = 0 , u ( t ) e [ - 1,1 ] , t e [ 0,0.78 ] .

Функции x 1 ( t ) , x ₂ ( t ) описывают соответственно отклонения температуры и концентрации. Управление u ( t ) характеризует поток хладагента, регулирующего необратимую экзотермическую реакцию.

В [10] Kirk D. E производит редукцию к задаче конечномерной оптимизации за счет дискретизации по функциям состояния и управления, замены производных конечными разностями по схеме Эйлера. Число моментов дискретизации не указано. В результате в [10] им были получены следующие результаты: x 1 ( 0.78 ) = - 6.167 х 10 ^{- 6} , x ₂ ( 0.78 ) = - 0.631 x 10 - 6 , Ф * ~ 0.00220 .

Приведем решаемую задачу к виду (1) - (3), т.е. со свободным правым концом, следуя методу штрафов, при достаточно большом фиксированном штрафном коэффициенте M >  0 :

Ф M = M (x12 (0.78) + x22 (0.78)) + x3 (0.78) ^ inf, x (t) = -2 (x1 + 0.25) + (x2 + 0.5) e^2 -(x1 + 0.25) u, x1 (0) = 0.05, x2 (t) = 0.5 -x2 -(x2 + 0.5) ё^, x2 (0) = 0, x3 (t) = x12 + x2, x3 (0) = 0 x1 (0.78) = 0, x2 (0.78) = 0, u (t)e[-1,1], t e[0,0.78].

Функция Понтрягина для данной образом:

задачи записывается следующим

H ( p , x , u , t ) =

25 x ₁

= p 1 - 2 ( x 1 + 0.25 ) + ( x ₂ + 0.5 ) e x ^{+ 2} - ( x 1 + 0.25 ) u

+

25 x ₁

+ P 2 0.5 — x 2 — ( x 2 + 0.5 ) e ^{1 + 2}

+ p 3 [ x ^{+ x} 2 ] .

Градиенты:

,        . 50 ( x ₂ + 0.5 ) 1 x 2 7 X

^Hx = ( P i ^- P 2) —---- "ГТ" ^e ' ^-( ^{2 + u} ) P i ^{+ 2} P 3 x i ^-

(xi + 2)

,„ \ (       \ 1°° ( x 2 + °'5 ) (23 - x )

⁽ H x i ) x ' =^{( P} ' " ^P 2 )------(^------ e' ^{+ 2 P} 3 -

H x , = ( P ' - P 2 ) - P 2 + 2 P 3 x 2 , ( H x 2 ), = 2 P 3 , H x 3 = 0 -

( H x 3 ) x = 0 - H u =- P i ( x + 0-25 ) -

Запишем получившуюся модифицированную сопряженную систему, вычислив r ( t ) и q по методу с условиями описанными выше:

,        х 50 (x2 + 0.5),

А = ( P 2 ^- P i ) —7—^е ' ⁺( ^{2 + u} ) P i ^{- (} x i + 2 )

. L       \50(x + 0.5)(23-x) 25x7) , ,

-

2p3xi - (Pi - p2)ex +2 + p3 y (t), (                 (xi + 2)

P' (0.78) = -2Mx' (0.78) - My (0.78),

25 x ₁

p 2 =( p 2- Pi) exi+2 + P 2 - 2 P 3x2 - P 3 У (t), p2 (0.78) = -2Mx2 (0.78) - My (0.78), p3 = 0, p3 (0.78) = -i.

где

y (t) = x (t, v)- x (t, u)

Будем решать с помощью проекционного метода нелокального улучшения (ПМНУ)

u*+1 (t) = P„ (u* (t) + aHu (pk (t),xk (t),uk (t),t)), t e T, где функции x* (t), pk (t) находятся в результате интегрирования фазовой и модифицированной сопряженной системы на текущем приближении. 5 (t ) = 0 так как задача линейна по управлению. В качестве начального приближения выбиралось управление u0 (t) = 1.

Проведем расчет ПМНУ для разных значений параметра a >  0 и штрафного коэффициента M >  0 . Наилучшее расчетное значение функционала Ф , вычисленное по методу ПМНУ, наблюдалось для параметров a = 0.13, M = 2 .

Значения a >  0 и M >  0	Значение Ф	x 1(0.78)	x 2(0.78)
a = 0.13, M = 2	0.00200330	- 9.62 х 10 - 4	1.24 х 10 - 3

Для сравнения проведем расчет также стандартным методом проекции градиента (МПГ) при M = 2 , u ⁰ ( t ) = 1 , где в схеме параметрической оптимизации применим метод золотого сечения с погрешностью 10 ^{- 3}. Получаем следующий результат x 1 (0.78) = 8.79 хЮ^{- 4}, x 2 (0.78) = 7.17 хЮ^{- 4}, Ф * » 0.00200 .

Рассчитывая же методом условного градиента (МУГ), с аналогичной погрешностью параметрической оптимизации, приходим к следующим результатам x 1 (0.78) = - 5.77 х 10 - 4 , x 2 (0.78) = 2.07 х 10 ^{- 3}, Ф * ~ 0.00200 .

Метод	Значение Ф	x 1(0.78)	x 2(0.78)
МПГ	0.00200084	8.79 х 10 — 4	7.17 х 10 — 4
МУГ	0.00199673	- 5.77 х 10 - 4	2.07 х 10 - 3

Для более удобного анализа приведем все решения в одной таблице:

Таблица 2. Сравнительный анализ эффективности
Метод	Значение ф	x 1 (0.78)	x 2 (0.78)	Число задач Коши
МПГ	0.002000	8.79 х 10 - 4	7.17 Х 10 - 4	101
МУГ	0.001997	- 5.77 х 10 - 4	2.07 х 10 - 3	96
ПМНУ	0.002003	- 9.62 х 10 - 4	1.24 х 10 - 3	90
Методом Kirk D. E	0.00220	- 6.16 х 10 6	- 0.63 х 10 - 6	--------

Скорость сходимости ПМНУ для различных значений M >  0 зависела от выбора значений параметра a >  0 . Например, для M = 2 сходимость наблюдалась при а е ( 0;0.4 ) , где при очень маленьких шагах скорость сходимости была медленной. Лучшая скорость по количеству решенных задач Коши наблюдалась для а е ( 0.10;0.14 ) . При увеличении штрафного параметра, приходилось уменьшать а . При этом скорость сходимости также падала.

На следующих рисунках представлен расчетный оптимальный процесс (итоговое управление u ( t ) и фазовые траектории x 1 ( t ) , x ₂( t ) ):

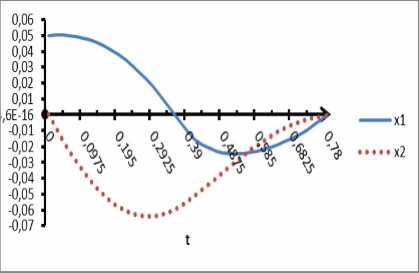
Рисунок 4 . Фазовые траектории

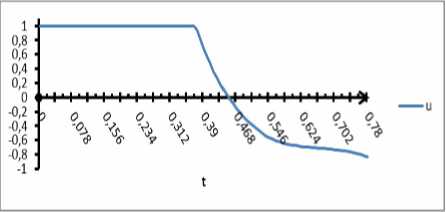
Рисунок 5 . Управление

Заключение

В рамках рассматриваемых расчетных задач рассматриваемый проекционный метод нелокального улучшения управления в целом показал лучшую эффективность по количеству расчетных задач Коши по сравнению с градиентными процедурами и другими методами, при приемлемой точности решения. При этом, в отличие от градиентных методов, требующих трудоемкую настройку процедур локального варьирования управления, настройка сходимости нелокального проекционного метода осуществляется только выбором одного настроечного параметра a >  0 .