Сравнительный анализ скользящих коэффициентов синхронности при анализе временных рядов

При изучении биологических процессов, сигналы, присутствующие во временных рядах различной природы (например, дендрохронологических рядах), ассоциру-ются либо с прямыми внешними периодическими воздействиями (например годовой освещенностью, солнечной иррадиацией и т. п.), либо с разнообразными внутренними нестабильными осцилляциями биологических систем, вызванными, например, возрастными изменениями последних [1-3].

При этом разделение влияния внешних (глобальных) и внутренних (локальных) сигналов при изучении различных временных рядов является достаточно сложной задачей [4; 5]. Например, в дендроклиматологии применяются различные процедуры статистической стандартизации дендрохронологических рядов, которые представляют собой временные ряды, построенные по ширине годичных колец. Такого рода статистическая обработка данных временных рядов позволяют частично решить поставленную проблему на региональном уровне [6; 7]. Если возникает задача выявления глобального сигнала на основе анализа динамики дендрохронологических рядов, распределенных на большой территории (например на севере России), то обычной стандартизации временных рядов будет недостаточно. Связано это с тем, что стандартизированные дендрохронологические ряды (древесно-кольцевые хронологии) сохраняют в себе остаточную информацию о различных процессах, которая в данном случае является уже шумом различной природы [3]. Такой шум может оказывать существенное воздействие на динамику изучаемых рядов и их спектральные характеристики. Это приводит к тому, что прямое сопоставление спектральных характеристик глобального природного процесса и различных его природных индикаторов не обнаруживает какой-либо статистической связи.

В работе анализируются скользящие характеристики синхронности временных рядов с точки зрения их устойчивости к шумовым воздействиям различного рода и их ассоциации с внешним периодическим воздействием.

В работе были использованы скользящий коэффициент конкордации Кендалла и средний скользящий коэффициент корреляции Пирсона.

Рассматриваемые характеристики применяются для расчета согласованности в поведении любой совокупности т временных рядов длины N.

Алгоритм расчета скользящего коэффициента конкордации аналогичен алгоритму расчета, предложенного Кендаллом [8] за исключением следующего: скользящий коэффициент конкордации С рассчитывается не для всего периода наблюдений N, а для каждого момента време ни t, который является центром скользящего окна с длиной W< N.

Коэффициент конкордации С изменяется в пределах от 0 до 1 . Ноль означает полную несогласованность в поведении временных рядов на рассматриваемом временном интервале. Соответственно, единица означает полную синхронность динамики анализируемых времен ных рядов.

Для расчета скользящего группового (осредненного) коэффициента корреляции Пирсона, предварительно необходимо рассчитать скользящие коэффициенты корреляции между всеми парами временных рядов i и j (V i ,у = 1_ т and ( i > J)) в момент времени t с шириной окна W = 2 к + 1, которые вычисляются по следующей формуле:

t + к

E ⁽ X i ( Р ) - X ( t ))( X -⁽ p ) - X - ⁽ t ))

^- t,W ⁾ = p"    ( W - DP a X

,

где x i ( t ) - оценка математического ожидания (средняя)

ВР x . в момент времени t ; a X - средне-квадратичное отклонение ВР х. в момент времени t ; х(t ) - оценка математического ожидания (средняя) ВР х . в момент времени t ; a X - средне-квадратичное отклонение ВР х в момент времени t .

И, окончательно,

ZZr-(t, W) / r (t, w ) = i-        m-—1.

/ e f

f = 1

Отметим также, что вычислялись значения скользящих коэффициентов только «полных» окон. Следовательно, скользящие коэффициенты не рассчитывались для начальных ( W - 1) / 2 и конечных ( W - 1) / 2 значений анализируемых временных рядов.

В результате внешнего воздействия или шума на сигнал, появляются отклонения от 1 в рассматриваемых значениях скользящих характеристик (это верно как для коэффициентов конкордации, так и корреляции). Следовательно, чувствительность к шуму той или иной характеристики можно оценить на основании отклонений от 1.

Такой оценкой может быть обычное евклидово расстояние D между временным рядом, все значения которого постоянны и равны 1 и соответствующим скользящим коэффициентом, т. е.

D = J1 (1 — C t )² ,

t где с - скользящий коэффициент конкордации или корреляции.

Если бы поведение рассматриваемых рядов было абсолютно несогласованным (или случайным), то все с = 0 и, следовательно, значение D было бы равно квадратному корню от длины исследуемого ряда (в нашем случае, в зависимости от окна W критические значения D колебались бы в пределах от 38,08 = д/ 1450 до 39,28 = 1543 ). Наоборот, в случае полной согласованности исследуемых временных рядов, значение D стремилось бы к 0. Таким образом, на основании евклидова расстояния можно ответить на несколько вопросов. Во-первых, является ли временная согласованность исследуемых рядов случайной или нет. Во-вторых, какая из скользящих характеристик менее подвержена влиянию шума, т. е. является более робастной по отношению к шумовым воздействиям различного рода. В-третьих, какая из скользящих характеристик более чувствительна к наличию сигнала. В последнем случае отметим, что это чувствительность будет определяться, прежде всего, величиной окна скольжения W . Очевидно, чем больше величина W , тем больше информации используется для получения той или иной характеристики и тем больше вероятность того, что скользящая характеристика «поймает» информацию об общем сигнале.

Дополнительным критерием для сравнения изучаемых скользящих характеристик может служить средний процент значимых значений. При определенных значениях окна скольжения W и количества анализируемых рядов т всегда можно найти критическое значение (при соответствующем уровне значимости ^ ) коэффициента конкордации (или корреляции) на основании известных распределений для соответствующих статистик. Следовательно, для каждого ряда скользящих коэффициентов можно рассчитать процент значимых значений. Следовательно, средний процент значимых коэффициентов конкордации (или корреляции) при определенных значениях ^и т можно получить осреднением соответствующих значений процентов, полученных для определенного количества анализируемых скользящих характеристик.

В качестве основных методов для спектрального разложения были использованы метод множественных сфероидальных последовательностей (multiple-taper methods -МТМ) [3; 9], сингулярный спектральный анализ (Singular Spectrum Analysis - SSA) [9] и Вейвлет анализ (Wavelet analysis) [10]. В отличии от традиционного преобразования Фурье эти методы могут быть применены к нестационарным временным рядам [3; 11]. Более того, эти методы могут эффективно выявлять сигнал в тех случаях, когда уровень шума во временных рядах высокий [3].

Для сравнительного анализа двух рассмотренных выше скользящих характеристик был использован следующий подход. Было решено проверить, насколько рассмотренные статистические характеристики чувствительны к шуму различного рода. Для этого были сгенерированы следующие наборы данных:

• 1.    Выборка 250 временных рядов длины 1550 лет, каждый из которых являлся аддитивной составляющей циклических компонент S t = sin(2 n 0,1667 1 ) + sin(2 n 0,05 t ) + + sin(2 n 0,0333 t ) + sin(2 n 0,01 1 ) (где t - время) и красного шума R. . Циклическая составляющая содержит следующие гармоники в 6,20, 30 и 100 лет. Напомним, что красный шум обычно описывается при помощи авторегрес

  сионного процесса 1 -го порядка AR (1): R . = р R _{( 1} + to _п , ( п = 0, ..., А ), где р - автокорреляционный коэффициент 1-го порядка: щ - гауссовский шум с математическим ожиданием R ₀ и дисперсией о ² (Allen, Smith, 1994). В качестве р было выбрано значение 0,6, которое является практически максимальным для различных природных процессов (Mann, Lees, 1996). Такой выбор обусловлен стремлением максимизировать уровень шума в исследуемых рядах.

• 2.    Выборка, представляющая собой 250 временных рядов, каждый из которых представляет собой белый (гауссовский) шум ( А (0,1));

• 3.    Красно-шумовая выборка того же объема.

• 4.    Выборка временных рядов, каждый из которых являлся аддитивной составляющей линейного тренда Tr_t = 0, 002t (где t - время) и красного шума с тем же параметром авторегрессии, что и в предыдущем пункте. Модуль величины тренда соответствует среднему тренду в различных временных рядах, полученных в дендроклиматологии.

• 5.    И наконец, множество временных рядов, представляющих собой сумму циклической составляющей S , тренда Тг и красного шума R .

Для каждого из описанных выше наборов были рассчитаны скользящие коэффициенты конкордации и ос-редненной корреляции с окнами ^ в 7, 11, 21, 51 и 101 году Кроме этого, рассматривалась зависимость динамики скользящих характеристик от количества временных рядов т , участвующих в расчетах для получения этих коэффициентов. Количество временных рядов варьировалось от 3 до 15.

Для получения достоверной информации о возможных различиях между указанными скользящими коэффициентами было решено получить средний (или обобщенный) скользящий коэффициент для каждой расчетной характеристики при фиксированном ^и т .

При этом для каждого синтетического набора из 250 временных рядов случайным образом выбиралось т рядов. Количество расчетных экспериментов при фиксированном т и W было равным 235. После этого полученные скользящие коэффициенты конкордации (или корреляции) для фиксированных т и ^усреднялись по времени (рис. 1).

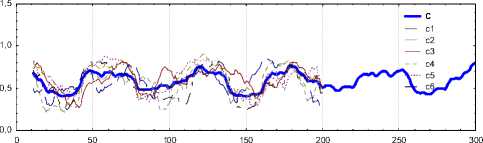
Рис. 1. Пример динамики скользящего коэффициента конкордации.

Коэффициент конкордации получен для т = 3 и Ж= 21 на интервале в 300 лет. Жирной линией обозначен средний коэффициент конкордации Кендалла С , полученный при усреднении 235 скользящих коэффициентов конкордации

Начнем сравнительный анализ между скользящими характеристиками с синтетического набора, который является совокупностью циклических составляющих и фонового красного шума (набор 1).

Во-первых, во всех рассматриваемых сериях в этом множестве присутствует один и тот же гармонический сигнал, причем вклад каждой из регулярных компонент одинаков в общую дисперсию сигнала. И если бы не наличие фонового красного шума, то анализируемые скользящие коэффициенты были бы постоянными и равными 1 вне зависимости от длины окна и количества вре менных рядов.

Во-вторых, в нашем случае уровень присутствующего шума очень высок и практически является максимальным для различных временных рядов, используемых в дендроклиматологии, климатологии. «Амплитуда» шума такая же, как и у циклических компонент, при этом уровень автокорреляции очень высок (Mann, Lees, 1996) и равен 0,6. Этот факт оказывает существенное влияние как на динамику регулярной компоненты (рис. 2), так и на динамику скользящих характеристик (рис. 3).

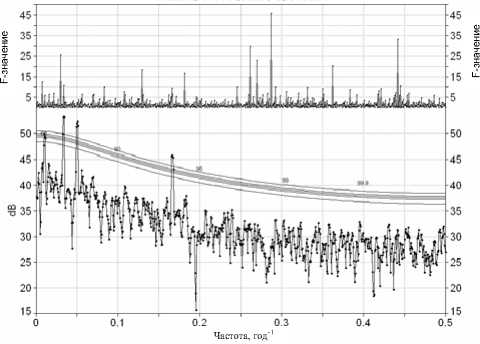
Рис. 2. Спектральное представление одной из 235 смоделированных циклических составляющих (с фоновым красным шумом AR(1) = 0,6), полученной при помощи МТМ подхода to 0.8

0,2

0.0

0          200         400         6 00         800         1 000        1200        1 400        1600

а

1,0

0,8

0,6

0,4

0,2

0,0

Согг 3 Согг 4 Согг 10 Corr 15

M^WVvWv^^ 0          200         400         600         800         1000        1200        1400        161

Гоч

б

Рис. 3. Пример динамики средних скользящих коэффициентов. а - скользящий коэффициент конкордации Кендалла; б - скользящий коэффициент конкордации Пирсона с окном W , равным 21 году и различным m (3, 4, 11 и 15 временных ряда)

Проанализируем динамику анализируемых скользящих коэффициентов.

Выявляется высокая значимая положительная корреляция между скользящими коэффициентами конкордации Кендалла и осредненной корреляцией Пирсона.

При этом в случае, когда в сериях точно присутствует гармонический сигнал, скользящий коэффициент корреляции практически не зависит от количества временных рядов т, используемых для его получения (рис. 3, б). В то же время коэффициент конкордации оказывается чувствительным к параметру т. Для этого коэффициента можно отметить одно общее свойство. С уменьшением числа т среднее значения коэффициента конкордации становиться выше (ближе к 1) при одном и том же значении окна W (рис. 4, а). Это также подтверждается значениями евклидова расстояния D (см. таблицу) - чем меньше число анализируемых рядов т, тем D ближе к 0.

Это, в свою очередь, означает, что скользящий коэффициент конкордации Кендалла может выявлять сигнал в анализируемых сериях даже в случае, когда уровень шума является практически максимальным, а число анализируемых временных рядов невелико .

Аналогичное свойство отсутствует для коэффициента корреляции. По сравнению с коэффициентом корреляции коэффициент конкордации проявляет свою чувствительность к сигналу уже при небольших значениях окна W .

В частности, средний процент значимых значений для коэффициента конкордации при ^= 11 годам, колеблется в пределах от 35 % (при т = 3) до 95 % (при т = 15) при относительно малых стандартных ошибках процентов (см. таблицу). Такое распределение точно отличается от случайного, что будет показано ниже. Таким образом, скользящий коэффициент конкордации Кендалла может выявлять сигнал в анализируемых «сильно зашумленных» временных рядах даже при небольших значениях окна скольжения W .

При увеличении окна W отличия между скользящими характеристиками нивелируются. Но даже при больших значениях окна, скользящий коэффициент конкордации продолжает быть более устойчивой к шуму характеристикой, так как существуют значимые отличия между абсолютными значениями D , рассчитанными для двух множеств реализаций изучаемых скользящих коэффициентов (одно множество - это множество скользящих коэффициентов конкордации Кендалла, другое - множество скользящих коэффициентов корреляции при фиксированной длине окна W , равного 51 или 101 году). Эти различия выявляются на базе дисперсионного и дискриминантного анализа.

Аналогичный анализ синтетического набора временных рядов, состоящего из композиции сигнала, тренда и красного шума (набор 5) не выявил новых результатов, кроме уже описанных.

Анализ других синтетических наборов данных, которые представляли собой временные ряды, состоящие из белого (набор 2), красного (набор 3) шумов и линейного тренда под воздействием красного шума (набор 4), не выявил каких-либо закономерностей в динамике обоих анализируемых скользящих коэффициентов. Все полученные коэффициенты конкордации и корреляции указывают на случайный характер согласованности в изучаемых временных рядах вне зависимости от их количества и окна скольжения.

Отметим, что даже максимальные значения анализируемых осредненных коэффициентов, полученных для наборов 2-4, являются не значимыми (р > 0,05).

Динамика скользящих коэффициентов корреляции для наборов 2-4 сильно зависит от количества временных рядов, используемых для его получения. С увеличением чис- ла временных рядов, амплитуда колебаний значительно уменьшается. Сравним этот результат с выводом для набора временных рядов 1 и 5 о независимости скользящего коэффициента корреляции от числа временных серий, если они являются комбинаций циклического сигнала и красного шума.

В целом, обнаруживается ряд существенных отличий, которые позволяют однозначно ответить на вопрос о наличии каких-либо закономерностей в динамике согласованности для наборов 2-4. Так, для рассматриваемых синтетических наборов данных средний процент значимых (с уровнем значимости р < 0,05) значений колебался от 4 до 15 % для коэффициента конкордации и от 1 до 5 % для коэффициента корреляции. Для набора 1, характеризующего сигнал, этот процент колебался от 36 (при W= 11, т = 3) до 100 % (при W= 51) для коэффициента конкордации и от 4 ( W= 11, т = 10; выше уже отмечалось, что осредненный коэффициент корреляции не работает при малых окнах) до 100 % (при W= 101).

Более того, для синтетических наборов 2,3,4 евклидово расстояние лежит в пределах от 26 до 39 (заметим, что максимальным евклидовым расстояниям между 1 и 0 будет, например, 39,23 при длине рядав 1543 года). В сравнении с синтетическим набором 1 или 5 соответствующее расстояние лежит в пределах от 13 до 25.

Таким образом, динамика рассматриваемых скользящих коэффициентов, полученных временных рядов, содержащих циклический сигнал, и рядов, не содержащих циклических компонент, значимо отличается друг от друга.

На основании проведенного анализа можно сделать следующие заключения:

• 1.    Рассмотренные скользящие коэффициенты конкордации Кендалла и осредненной корреляции Пирсона обладают рядом интересных свойств, связанных с их способностью выявлять сигнал даже в сильно зашумленных временных рядах. Причем коэффициент конкордации может распознавать сигнал даже при меньшем количестве анализируемых временных рядов и меньшей величине окна скольжения по сравнению с осредненным коэффициентом корреляции.

• 2.    Частотный диапазон коэффициента конкордации при различной длине окна скольжения полностью характеризует диапазон исходного сигнала с учетом «новых» пиков спектрограммы, которые образуются в результате нелинейного взаимодействия базовых частот. При этом различные окна скольжения не добавляют «искусственных» пиков.

• 3.    Экспериментально доказано, что существуют значимые отличия в динамике скользящих коэффициентов конкордации Кендалла (и осредненной корреляции Пирсона), полученных, с одной стороны, для временных рядов, содержащих циклическую составляющую, с другой, для временных рядов, содержащих только шум или тренд и шум в совокупности. Эти отличия могут быть выявлены при помощи проверки статистических гипотез на значимость изучаемых коэффициентов и критерия, основанного на сравнении евклидовых расстояний.

Рассмотренные скользящие характеристики, робастные к шумовым воздействиям различного рода, могут оказаться эффективным инструментом для выявления закономерностей локального и глобального характера при анализе пространственно-распределенных временных рядов различной природы, в частности, дендрохроноло-

Статистические характеристики, полученные при осреднении 235 моделируемых скользящих коэффициентов конкордации Кендалла и корреляции Пирсона

Длина окна W	Число ВР т	Евклидово расстояние для средней конкордации	Евклидово расстояние для средней корреляции	Средний процент значимых значений коэффициентов конкордации (р < 0,05)	Стандартное отклонение для предыдущего процента	Средний процент значимых значений коэффициентов корреляции (р < 0,05)	Стандартное отклонение для предыдущего процента
11	3	19,0	27,8	35,3	2,8	12,1	1,6
	4	21,4	27,7	50,2	3,5	9,0	1,5
	10	25,6	27,7	86,3	2,4	4,1	0,9
	15	26,5	27,7	9,3	1,1	2,8	0,7
21	3	16,6	24,3	66,4	5,4	45,7	5,1
	4	18,5	24,2	79,7	3,1	45,0	3,9
	10	22,3	24,2	98,2	0,9	44,9	2,6
	15	23,1	24,2	99,8	0,3	45,1	3,3
51	3	14,5	21,1	97,6	4,0	92,0	3,6
	4	16,3	21,2	99,6	1,6	94,1	8,5
	10	19,7	21,2	100,0	0,0	98,6	1,6
	15	20,4	21,1	100,0	0,0	99,2	0,5
101	3	13,9	20,2	99,7	3,8	99,1	6,6
	4	15,5	20,2	99,9	0,7	99,3	5,3
	10	18,6	20,1	100,0	0,0	100,0	0,0
	15	19,3	20,1	100,0	0,0	100,0	0,0

гических рядов, рядов инструментальных климатических наблюдений и различных климатических реконструкций за последние несколько тысячелетий [3; 4; 6; 7; 12]. В свою очередь, такие закономерности позволяют калибровать различные глобальные климатические модели.

Работа выполнена при финансовой поддержке проекта РФФИ № 06-05-64095-а, проекта «Научная школа» (код проекта НШ - 8208.2006.4) и проекта Royal Society NATO/FSO postdoctoral fellowship 04-15845.