Сравнительный анализ свойств кривых ползучести, порождаемых линейной и нелинейной теориями наследственности при ступенчатых нагружениях

DOI:

Нелинейное определяющее соотношение (ОС) Работнова [1; 2; 4; 8; 10; 12–19; 23–26] описывает одномерные изотермические процессы деформирования структурно-стабильных

(нестареющих) реономных материалов, связывая истории напряжения σ( t ) и деформации ε( t ) в данной точке тела:

tt

Ф(е( t )) = J П ( t - т) d о(т) , o( t ) = J R ( t - т) ф ' (е(т)) d е(т) , t >  0 ,                (1)

где П ( t ) , R ( t ) - функции ползучести и релаксации (ФП и ФР), а ф( и ) - дополнительная МФ, введенная Работновым. Входные процессы ( σ( t ) или ε( t ) ) предполагаются кусочнонепрерывными и кусочно-гладкими на любом отрезке. Определяющее соотношение (ОС) (1) обобщает линейное ОС вязкоупругости, инвариантное относительно сдвигов по времени:

tt

е( t ) = J П ( t - т) d о(т) , о( t ) = J R ( t - т) d е(т) , t >  0 .                     (2)

Если П (0 + ) ^ 0 (модель регулярна), то R (0 + ) < да и на пространстве непрерывных кусочно-гладких при t >  0 функций (взаимно обратные) операторы (1) (и (2)) представимы в виде tt

Ф(е( t )) = П (0)о( t ) + J П ( t - т) о(т) d т , о( t ) = R (0)ф(е( t )) + J R ( t - т) ф(е(т)) d т ,         (3)

где у (0) - краткое обозначение для предела справа у (0 + ) функции y ( t ) в т. t = 0 . ОС (3), обобщающее линейное ОС (2) с регулярной ФП путем введения МФ φ , было предложено Ю.Н. Работновым в 1948 году [13]. В [10] оно называлось «соотношением наследственной теории пластичности» и «ползучести», в монографии [17, с. 209] – «наследственной теорией ползучести», в [18] было дано название «нелинейная теория наследственности». В англоязычных работах ОС (1) называется уравнением квазилинейной вязкоупругости («QLV») [27; 42–44; 48; 49; 51; 52; 55; 56; 58–61; 63], а его автором часто называется Y.C. Fung со ссылкой на его работы 1970–1990-х годов [55; 56]. В [1; 2; 4; 8; 10; 12–19; 23–26] ОС (1) прилагалось к описанию поведения стеклопластиков, графита, металлов, сплавов и композитов при разных режимах деформирования, а в [27; 42–44; 48; 49; 51; 52; 55; 56; 58–61; 63] – поведения связок, сухожилий и других биологических тканей (см. более подробный обзор в [28; 36]). Тщательное аналитическое изучение общих свойств основных теоретических квазистатических кривых (ползучести, релаксации, деформирования и т. п.) ОС (1) с произвольными МФ П и ф , систематическое исследование комплекса моделируемых эффектов в зависимости от характеристик МФ и необходимых феноменологических ограничений на МФ φ (и следствий из них) не проводились в [1; 2; 4; 8; 10; 12–19; 23–26; 27; 42–44; 48; 49; 51; 52; 55; 56; 58–61; 63]; границы области применимости ОС (1) и их маркеры (за исключением требования подобия изохронных кривых ползучести в [1; 2; 4; 8; 10; 12–15] и подобия кривых релаксации в [51; 52; 58]) выявлены не были.

Цель данной статьи (а также цикла работ [28; 31; 36; 37; 41] и др.) – восполнить эти пробелы, выявить возможности и преимущества ОС (1) (как по сравнению с линейным ОС (2), так и с более сложными нелинейными ОС) и содействовать расширению и уточнению сферы его обоснованного применения в моделировании поведения реономных материалов с выраженной нелинейной наследственностью и скоростной чувствительностью (полимеров, композитов, пен, геотканей, керамик, асфальтобетонов, твердых топлив, алюминиевых и титановых сплавов, нержавеющих сталей, связок, сухожилий, стенок сосудов и других биологических тканей и т. п.).

Испытания на ползучесть при ступенчатых нагружениях (с кусочно-постоянным напряжением) – важный вид квазистатических испытаний, позволяющий уловить и обследовать разные аспекты поведения материала и детали реализации многих эффектов [3; 5; 6; 9; 17; 19; 22; 45; 46; 54; 58; 62], собрать более богатую информацию для выбора, идентификации и верификации определяющих соотношений по сравнению с кривыми ползучести (КП) при постоянном напряжении (такие КП все модели описывают адекватно при правильной настройке). В частности, они позволяют обнаружить признаки нелинейности в поведении материала, исследовать зависимость кривых ползучести от уровня напряжения и предыстории нагружения, восстановление и остаточную деформацию при полной и частичной разгрузке, влияние параметров начальной стадии нагружения и перестановки ступеней нагружения, скорость затухания памяти, эффекты, сопровождающие скачок напряжения вниз или его быстрое убывание за малый промежуток времени (dip tests, non-monotonic creep behavior), влияние скачков напряжения на длительную прочность и отклонение от правила линейного суммирования поврежденности (Miner’s rule, linear damage rule, cumulative damage theory) [3; 5; 6; 9; 14; 17; 19; 22; 28; 29; 32; 35; 38; 45–54; 57; 58; 62].

Задача данной статьи – анализ и сопоставление общих свойств кривых ползучести при ступенчатых нагружениях, порожденных ОС (1) и (2) с произвольными МФ П и ф (связи скачков в точках разрыва программы нагружения, асимптотики КП, накопления пластической деформации, условий затухания памяти [32; 40], влияния перестановки ступеней нагружения и т. п.), – как унаследованных от КП линейного ОС (2) ([29; 32; 34]), так и новых.

В статье приняты следующие сокращения и обозначения: ФР и ФП – функции релаксации и ползучести; (щ ;щ + ) и ( x ; x ) - области определения и значений МФ ф( и ) ; Ф = ф ^{- 1} ; h( t ) -функция Хевисайда; 5( t ) - дельта-функция; РеМ - регулярные модели (с ФП: П (0) * 0 ); СиМ - сингулярные модели (ФР содержит слагаемое n5( t ) ); У(t * )^: = У ( t * + 0) — У ( t * — 0) -скачок y ( t ) в т. t _* .

Об ограничениях на материальные функции соотношения (1)

Линейное ОС вязкоупругости (2) получается из (1) при ф( и ) = и и содержит лишь одну независимую МФ, так как ФП и ФР связаны условием взаимной обратности интегральных операторов (2) («the interconversion relation»):

tt

J П ( t - т) R (т) d т = t , или J П ( t - т) R (т) d т + П (0) R ( t ) = 1 . (4) 00

Зная ФР, можно найти ФП из уравнения (4), и наоборот. Поэтому из трех МФ ф , П , R ОС (1) лишь две независимы, а тождество (4) является условием взаимной обратности операторов (1), отображающих друг в друга функции о( t ) и e ( t ) = ф(г( t )) . На ФП и ФР в ОС (1) наложим априори те же минимальные ограничения, что и в линейной теории: П ( t ) и R ( t ) предполагаются положительными и дифференцируемыми на (0; да ) , ФП П ( t ) - возрастающей и выпуклой вверх [34], а ФР R ( t ) - убывающей и выпуклой вниз на (0; да ) , ФР может иметь интегрируемую особенность или 5 -сингулярность в т. t = 0 (слагаемое n5( t ) ). Из этих условий, в частности, следует существование пределов П (0 + ) = inf П ( t ) >  0 , R (0 + ) = sup R ( t ) >  0 ( R (0 + ) = +да , если ФР не ограничена сверху) и П ( +да ) >  0 и R ( +да ) >  0 [34].

Свойства основных теоретических кривых линейного ОС (2) с произвольной ФП, необходимые математические и феноменологические ограничения на ФП и ФР проанализированы в цикле работ [29; 30; 32–34; 39] и др. Анализ, в частности, показал, что среди моделей, описываемых ОС (2) с произвольными ФР и ФП, необходимо выделять (как минимум) три основных класса, ибо качественные свойства базовых теоретических кривых моделей этих классов (а также особенности постановки и решения краевых задач) заметно отличаются: 1) регулярные модели (РеМ) - у которых П (0) Ф 0 (тогда мгновенный модуль E = R(0 + ) = 1/ П (0 + ) конечен, а ОС (2) и первое уравнение (4) сводятся к уравнениям Вольтерры второго рода (3) с ф( u ) = и и (4)); 2) сингулярные (СиМ) - с ФР, содержащей слагаемое п§( t ) , П >  0 (ФР R = П^( t ) задает ньютоновскую жидкость с ОС о = рс и входит слагаемым в ФР «половины» реологических моделей из пружин и демпферов), тогда П (0) = 0 и П (0) = п — ¹ ; 3) нерегулярные модели с неограниченной ФР, не содержащей слагаемое ηδ( t ) , но имеющей интегрируемую особенность в точке t = 0 ( R (0 + ) = +го ). Третий класс занимает промежуточное положение между первыми двумя. К нему относится, например, ФР R ( t ) = At ^{— и} , и g (0;1) , A >  0 , задающая так называемый «фрактальный» элемент «фрактальных» моделей (“fractional models”); соответствующая (в силу (4)) ФП имеет вид П ( t ) = A C ( и ) t ^u и обладает не только свойством П (0) = 0 , как и СиМ, но и свойством П (0) = го , переходным к П (0) Ф 0 , характеризующему РеМ.

Линейным ОС (2) задаются, в частности, все модели, собранные из линейных пружин и демпферов посредством параллельных и последовательных соединений (ФП классических моделей будут использованы для иллюстрации общих свойств КП ОС (1)). Схемы и названия всех двух-, трех- и четырехзвенных моделей (в терминологии нет единства) приведены в [39, рис. 1]. Можно доказать, что множество всех несократимых n -звенных моделей распадается ровно на два класса эквивалентности: РеМ- n и СиМ- n (структурно различные модели эквивалентны, если задаются одинаковыми семействами ФП или ФР). В частности, эквивалентны друг другу трехзвенные РеМ Пойнтинга-Томсона и Кельвина [39, рис. 1а], а все четыре РеМ-4 [39, рис. 1в] эквивалентны модели стандартного тела (последовательному соединению моделей Максвелла и Фойгта, то есть РеМ-2 и СиМ-2). Например, семейство

П ( t ) = a t + в - Y e , Х >  0 , а,в >  0 , y g [0,в] , (5) удовлетворяет всем ограничениям, налагаемым на ФП. Оно порождает все РеМ-4 при y g (0; в) , а,в >  0 , а при a = 0 - все РеМ-3. Так как П (0) = в - Y , то ФП (5) порождает СиМ, когда в = Y : при Хв = 0 - ньютоновскую жидкость, при a = 0 - модель Фойгта, при a >  0 - все СиМ-3 ( R = п§( t ) + Ee ^v t ). При y = 0 (5) дает модель Максвелла.

На МФ φ(u) в ОС (1) наложим следующие минимальные первичные требования [28; 31; 36; 37; 41]: ф(и), и g(to-;to+), непрерывно дифференцируема и строго возрастает на (to- ;0) U (0;to+) (где to—to+< 0), причем ф(0+) = ф(0—) = 0 (иначе входному процессу с(t) = 0 соответствует ненулевой отклик о(t)). Формально возможны случаи to- = —го, to+ = +го и ф'(0) = +го. Для материалов с одинаковым поведением при растяжении и сжатии МФ ф нечетна и to— = —to+. Из возрастания ф(и) следует существование обратной функции Ф := ф—1 на промежутке DФ = (x; x), где x := sup ф(и) = ф(to+ — 0), x := inf ф(и) = ф(to— + 0), 30 А.В. Хохлов. Сравнительный анализ свойств кривых ползучести и обратимость ОС (1). Величины X и x - важные характеристики МФ ф и Ф , существенно влияющие на поведение теоретических кривых ОС (1) [28; 31; 36; 37; 41].

Для задания МФ ф или Ф удобно, например, семейство функций у (х) = A[3( x / C) n + (1-Э)(x / C) m ], x > 0, n > 1, m < 1, Эе [0;1], A, C > 0.       (6)

При всех значениях пяти параметров (кроме Э = 0;1) у(0) = 0, у'(0) =да, у(С) = A , у(x) возрастает и имеет точку перегиба x = Cq(n, m, Э)1/(n-m), q := m(1 - m)(1 - Э)[n (n -1) Э]-1.                   (7)

Действительно, у '( x ) = AC ¹ [ n Э( x / C ) n ^{- 1} + m (1 - Э)( x / C ) ^{m - 1}] , у '( x ) = Ax - 2 [ n ( n - 1)Э( x / C ) n + m ( m -1)(1 - Э)( x / C ) ^m ] , у "( x ) = 0 равносильно (7). Весовой параметр Э е (0;1) позволяет совместить точку перегиба x с любой точкой x >  0 (и описать КП со всеми тремя стадиями [36]); семейство (6) убывает по Э на интервале x е (0; C ) и возрастает на ( C ; да ) ). В случае m = 1/ n (7) принимает вид x = C [( Э - ¹ - 1) n ^{- 3} ] ” ^/( ” ^{- 1)} . При Э = 0,5 x = Cn ^{- 3 n /( n - 1)} и потому при n ^ 1 x c ^ Ce ^-L5, а при n ^да xc ^ C . Очевидно, при n ^ 1 + 0 семейство (6) с m = 1/ n стремится к линейной функции у = AC - x , то есть МФ ф или Ф в ОС (1) «исчезает» и нелинейное ОС превращается в линейное ОС (2).

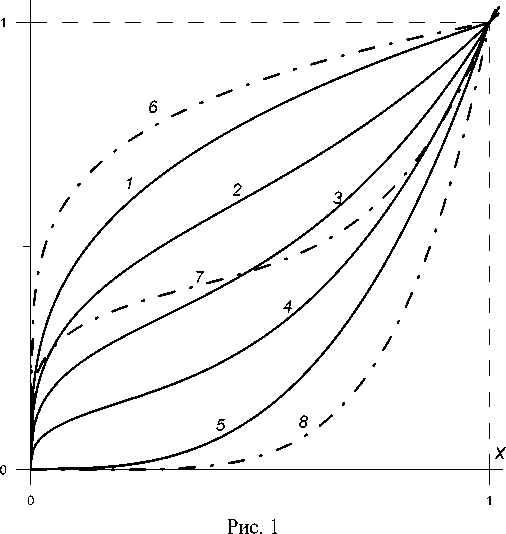
На рисунке 1 приведены графики функций (6) с m = 1/ n , n = 3 , A = C = 1 и Э = 0;0,25; 0,5; 0,75; 1 (кривые 1-5 ) и графики при n = 5 и Э = 0;0,5;1 (кривые 6-8 ). С ростом n производные ф( x ) в окрестностях точек x = 0 и x = 1 возрастают.

При и <  0 можно определить ф( и ) формулой ф( и ) = - у ( - и ) , причем для разносопротивляющегося материала можно взять другой набор пяти параметров функции (6) (при этом начальные условия у (0) = 0 , у ' (0) = да обеспечивают гладкую склейку МФ ф в точке и = 0 ).

Кривые ползучести при постоянном напряжении

КП ОС (1) при мгновенном нагружении о( t ) = 5h( t ) , 5 >  0 , имеют вид:

е( t ,5) = Ф (5 П ( t )) при 5 П ( t ) <  x ,                               (8)

где Ф : = ф ^{- 1} , x : = sup ф( и ) - верхняя грань области определения Ф ( x ) . Семейство КП (8) возрастает по 5 (так как Ф возрастает), а при любом 5 >  0 КП возрастает по t на всем промежутке, где 5 П ( t ) <  x .

Если x = да (как для линейного ОС, например), то D _Ф = [ x ; да ) и КП определены при всех 5 >  0 и t >  0 . Если же x <да , то 5 П ( t ) е D _Ф только при 5 <  x / П (0) &  П ( t ) <  x / 5 ; это означает, что КП существует только для напряжений о <  5 * , о * : = x / П (0) и обрывается в момент t * , удовлетворяющий уравнению П ( t * ) = x / ст , если 5 >  x / П ( да ) (если П(да) < да, КП с малым 5 не обрывается). Таким образом, если x <да и П (0) * 0 , то параметр 5 * : = x / П (0) = Ex можно трактовать как предел (мгновенной) прочности при растяжении (если для моделируемого материала характерно разрушение, растрескивание или резкое изменение свойств при некотором критическом напряжении), и в ОС (1) уже встроен критерий разрушения. Если Ф ( x ) < да , то есть to + <да , разрушение при растяжении происходит по достижению критической деформации: е * : = Ф ( x ) = to + (такой физический смысл можно придать параметру to + ). Уравнение кривой длительной прочности при растяжении: t * = p ( x /ст) , Е _да x <  5 <  Ex , где E : = 1/ П (0) , E _да : = 1/ П ( да ) - мгновенный и длительный модули линейного ОС (2) [39]. Из ограничений, наложенных на ФП, следует, что t _*( σ ) убывает (как и экспериментальные КДП), выпукла вниз и t * (5) ^да при с ^ Е _да x . Отметим, что МФ φ ( x ) практически не влияет на форму (и качественные свойства) кривых длительной прочности: лишь скалярный параметр x управляет растяжением кривых вдоль оси напряжения.

КП линейного ОС (2) всегда выпуклы вверх на всем луче t >  0 (и потому оно не способно описывать поведение материалов, кривая ползучести которых включает стадию ускоряющейся ползучести [34]), а скорость ползучести всегда стремится при t ^ да к конечному пределу V (5) = 5 v , v : = П ( да ) . Из наличия МФ ф в ОС (1) вытекают следующие качественные отличия свойств его КП по сравнению с КП линейного ОС (2) [36]: 1) зависимость КП (и скорости ползучести) от С не линейная (изохронные КП не прямолинейны) и задается МФ Ф = ф 1 ; 2) КП не обязаны быть выпуклыми вверх, возможно наличие точек перегиба и моделирование КП со всеми тремя стадиями; для нелинейного ОС возможен случай стремления скорости ползучести к бесконечности как при t ^ да , так и при t ^ t * . 3) Если x <да , то в ОС (1) встроен критерий разрушения, обеспечивающий обрыв КП и позволяющий моделировать длительную прочность. Подробный анализ свойств кривых ползучести и длительной прочности, порождаемых ОС (1), проведен в работах [36; 37]. Разнообразие форм КП, которое позволяет получить вторая МФ φ ОС (1) по сравнению с КП линейного ОС (2), проиллюстрировано в работе [36] и на рисунке 2.

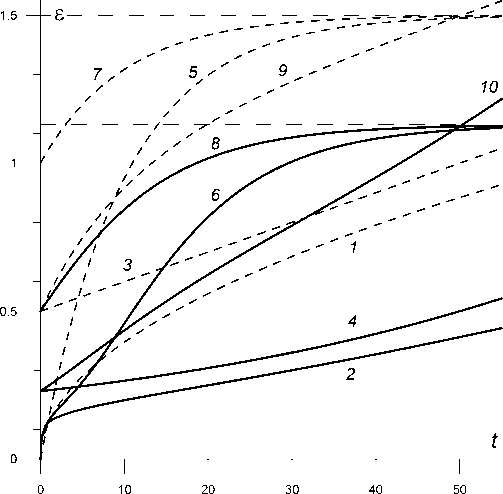
Рис. 2

На рисунке 2 приведены КП (8) (с 5 = 1 ) линейной модели с ФП П ( t ) = t ^0,5 /8 (кривая 1 ), четырех линейных моделей вида (5): РеМ-2 (Максвелла) с у = 0 , а = 0,01 , в = 1 , СиМ-2 (Фойгта) с а = 0 , в = Y = 1,5 , X = 0,1, РеМ-3 (Кельвина) с а = 0 , в = 1 , Y = 0,5 , X = 0,1 (стем же временем ретардации т = Л = 10 ), РеМ-4 с X = 0,1, в = 1 , Y = 0,5 , а = 0,01 (кривые 3, 5, 7, 9 ) и КП пяти нелинейных моделей с

Ф ( x ) = A (0,5 x n + 0,5 x¹ n )

при A = 0,5 , n = 3 и теми же ФП (кривые 2, 4, 6, 8, 10 ). У КП 2, 4, 6, 10 есть участки выпуклости вниз, КП 2 (модели со степенной ФП) содержит все три типичные стадии ползучести, КП 6, 8 обладают горизонтальными асимптотами (как и 5, 7 ). Значения относительной деформации указаны в процентах. По оси абсцисс отложено безразмерное время; рассматриваемые качественные свойства кривых (монотонность, выпуклость, ограниченность и горизонтальные асимптоты КП, величины пределов и скачков деформации) не зависят от его конкретного масштабирования (инвариантны относительно сжатия оси времени).

Общее уравнение кривых ползучести для ступенчатых нагружений

Рассмотрим кусочно-постоянную программу нагружения с n ступеньками n-1

°( t ) = Е ° i ^[h( t ^- t i - 1 ) ^{- h(} t ^- t i ^{)] +} ° n ^h( t ^- t n - 1 ) ,                        (10)

i = 1

где t ₀ = 0 , t i >  t i - 1 , °( t ) = о i при t e ( t i - 1 , t i ) и °( t ) = о _n при t >  t_n - 1 . Так как оператор (1), переводящий процесс σ( t ) в φ(ε( t )) , линеен и инвариантен относительно сдвигов по времени, он переводит (10) в сумму откликов на каждую ступеньку:

n - 1

ф(е( t )) = Е ° i S ( t ^- t i - 1 ; ti ^- ti - 1 ) ⁺ ° n ^{n (} t ^- t n - 1^)h( t ^- t n - 1 ) ,                  (11)

i = 1

где 5(t; T) := П(t)h(t) -П(t - T)h(t - T) - отклик на единичную ступеньку напряжения с носителем [0,T] (задающий форму кривой обратной ползучести линейного ОС (2)). Тогда n-1

е( t ) =^{ф (} Е ° t ^{5 (} t ^- ti - 1 ; t ^- ti - i ) + ° n ^{п (} t ^- t n - i^)h( t ^- t n - 1 ) ) , t >  0 ,               ⁽¹²⁾

i = 1

где Ф = ф 1 . Вычисление деформации по формуле (12) возможно лишь при тех t , при которых значение правой части выражения (11) принадлежит D _Ф = ( x ; x ) . В противном случае отклик ε( t ) не определен, и это можно интерпретировать как разрушение, происходящее в момент t = t * , когда (впервые) происходит выход за пределы интервала D _o . Если x и x бесконечны, то есть область значения МФ φ( u ) – вся ось (как в случае линейного ОС (2)), то для программ нагружения (10) с любыми t i и σ i формула (12) справедлива для всех t >  0 . Именно этот случай мы и будем рассматривать, чтобы не осложнять формулировки дополнительными ограничениями на программы (10), необходимыми в случае конечности x или x .

Уравнение КП (11) можно представить в виде суммы влияний скачков напряжения n - 1

°i := °i+1 - °i (°o := 0) в точках ti : ф(е(t)) = ^ °t П(t - ti )h(t - ti) , t > 0, или i=0

i

^£ ( t ) = ^{ф (} ° 1 ^{П (} t ) + ^ ° k ^{n (} t ^- t k )) при t e ⁽ t ; t + 1 ) .                     (13)

k = 1

Зависимость между скачками и влияние ползучести на скачки упругой деформации (эффект «дрейфа»)

В точках разрыва t = t, программы нагружения (10) деформация (12) и ее производная, вообще говоря, имеют разрывы ( ε( t ) – первого рода). Из (13) можно выразить пределы ε( t ) в точках t = t , слева и справа и скачок £( t, ) :

е( t - 0) = Ф ( p ) , е( t + 0) = Ф ( p_z + ° П (0)) ,

- 1

p * := °1П( ti)■ Е ° кп( ti- tk), k=1

£⁽ t ) = ^{ф (} p_t + ° , ^{п (0)) -ф (} P i ) , i = 1,..., n - 1 .                      (14)

У нерегулярных моделей (тех, у которых П (0) = 0 , в частности, у СиМ- n и степенных моделей) e( t _i ) = 0 , то есть КП (12) непрерывны во всех т. t = t _i , как и в случае линейного ОС. Однако у регулярных нелинейных моделей скачки (14) ненулевые и зависят от всех параметров программы нагружения с номером, не превосходящим ; скачок εˆ( t ) возрастает с ростом скачка напряжения ° _z- и совпадает с ним по знаку (так как МФ Ф возрастает).

В случае линейного ОС (2) с непрерывными П(t) и R(t) скачки КП (12) и ее производной выражаются формулами e(t ) = °zn(0), £(t ) = °Д(0) [32], то есть скачок процесса-отклика в любой момент ti линейно (и локально) зависит только от величины скачка программы нагружения (и ее производных) в этот же момент времени и не зависит от ti , от предыстории (от всех tk и оk при k < i) и от ФП П(t) (зависит только от ее начальных значений П(0) и П(0)). В частности, модуль скачка с(t) не меняется при смене знака скачка нагрузки. Эти свойства можно использовать как индикаторы (не)применимости линейного ОС (2): например, в испытаниях сплавов алюминия зафиксировано [47], что модуль скачка деформации вниз в момент сброса нагрузки меньше, чем скачок вверх в момент догрузки, и потому поведение этих материалов не описывается ОС (2).

Для КП регулярных нелинейных моделей (1) все обстоит иначе: зависимость (14) скачков КП от всех параметров программы нагружения и ФП П ( t ) отличается от линейного случая не только нелинейностью, но и нелокальностью. Из формулы (14) следует, что | εˆ( t_i ) | зависит от знака скачка нагрузки о _z в момент t = t_z : | е( t_z )| при разгрузке может быть больше или меньше, чем при догрузке, в зависимости от знака Ф" ( x ) на интервале ( p_t — о _z П (0); p_z + о _z П (0)) . Это делает возможным моделирование эффекта влияния ползучести (то есть предыстории нагружения и накопленной деформации) на скачки упругой деформации, порожденные «мгновенным» изменением напряжения в некоторый момент. Этот эффект зарегистрирован в испытаниях сплавов алюминия, композитов, костной ткани [7; 20; 21; 47]; в работе [21] он назван «дрейфом мгновенно-упругой деформации вследствие ползучести». В частности, этот эффект проявляется в том, что абсолютная величина скачка деформации в момент сброса нагрузки отличается от ее скачка при нагрузке (догрузке). Линейное ОС с произвольной функцией ползучести в принципе не способно моделировать явление дрейфа.

Асимптотика кривых ползучести, остаточная деформация и асимптотическая коммутативность

Исследуем асимптотику КП (12) при t ^ да (для моделей с D _ф = ( —да ; да ) , когда КП (12) определена для всех t >  0 ). Так как для произвольной допустимой ФП S ( t ; T ) ^ vT при t > да , v : = ^{п ( да )} [32], то S ⁽ t ^— t - 1 ; t ^— t - 1 ) = v ⁽ t ^— t - 1 ) + о ⁽¹⁾ ,

2 5z S(t — tz—i; tz — tz-1) = vs + z(t), где 5 := ^ 5z (tz — tz-1), z(t) = o(1) при t > да. i=1

Поэтому КП (12) представима в виде:

e( t) = Ф(о n П( t—tn—1) + vs + z (t)), где z (t) = o (1) при t >да,(15)

а отклонение КП (12) от КП е₀( t ) = Ф (о n П ( t — t n _{— 1})) , соответствующей мгновенному нагружению до уровня о n в момент t n _{— 1} (с нулевой предысторией), - в виде

А(t) = Ф(оnП(t — tn—1) + vs + z(t)) — Ф(оnП(t — tn—1)), t > tn—1.(16)

Перестановка ступеней нагружения с z <  n не влияет на величину s и асимптотики (15), (16). Для линейного ОС (2) А ( t ) = vs + z ( t ) , а величина £ _да = vs имеет смысл остаточной деформации после полной разгрузки (случай о _n = 0 ) и восстановления при t ^ да .

Параметр vs (наряду с σ _n ) управляет асимптотикой конкретной КП (12), а параметр v – характером асимптотик всех КП (12) и отклонений (16) для произвольных ступенчатых программ нагружений (10). Если v = 0 (и о n ^ 0 ), то по (15) и (16) £( t ) = Ф (о n П ( t - t n - 1 ) + z ( t )) и

A(t) = ф(оnn(t-tn-1) + z(t))-ф(оnn(t-tn-1)), где z(t) = о(1) при t ^да. (17)

Из асимптотических представлений (15)–(17) вытекает формула для остаточной деформации при полной разгрузке в момент t n 1 (программа нагружения (10) с о _n = 0 ) и ряд других важных следствий о поведении отклонения (16) при t ^да , отклонений КП с одинаковыми σ _n друг от друга, в частности, о влиянии перестановки ступеней нагружения [28].

Еще Одквистом [11] было подмечено (а затем проверялось в испытаниях), что в теории ползучести с упрочнением вида £ = g (£) f (о) (когда переменные г и о разделяются) справедливо свойство коммутативности при двухступенчатом нагружении [17, с. 217]: для двух программ нагружения, отличающихся порядком приложения напряжений σ₁ и σ₂ в течение одинакового времени T , деформация в момент t = 2T будет одна и та же: £₁₂(2 T ) = £₂₁(2 T ) • В испытаниях материалов это свойство не выполняется, а наблюдается £₁₂(2 T ) >  £₂₁(2 T ) для о₂ >  о 1 [6, с. 42; 17, с. 218]. В [32] доказано, что линейное ОС (2) с произвольной выпуклой вверх ФП воспроизводит этот эффект и всегда дает £₁₂(2 T ) >  £₂₁(2 T ) для любых T , о 1 >  о₂ , но при t ^да для любого о₃ , действующего при t >  2T , отклонение £₁₂( t ,о₃) — £₂₁( t ,о₃) стремится к нулю (см. рис. 3). Последнее свойство мы будем называть асимптотической коммутативностью ОС (2) при перестановке ступеней нагружения (упоминания о нем отсутствуют в литературе).

Теорема 1. Пусть ФП П ( t ) положительна, дифференцируема, возрастает и (нестрого) выпукла вверх на (0; да ) , а МФ ф( и ) непрерывно дифференцируема и строго возрастает на (to - ;0) U (0;ю ₊ ) (возможно to - =-да и ю + =+да ), ф(0 + ) = ф(0 - ) = 0 и область значений ф( и ) совпадает с ( -да ; +да ) (то есть D _ф = ( -да ; +да ) ). Тогда КП (12) нелинейного ОС (1) для любой ступенчатой программы нагружения (10) определена при всех t >  0 и обладает свойствами:

• 1)    если Ф' ( x ) ограничена сверху на полуоси [0; да ) (то есть ф ' ( и ) >  у >  0 ), то для любых двух программ вида (10) с одинаковыми конечными уровнями напряжения σ _n , моментами их включения T = t n - 1 ( n произвольно) и значениями s разность откликов (КП (12)) £ 1 ( t ) - £₂( t ) стремится к нулю при t ^ да ; в частности, при перестановке ступеней нагружения с номером i <  n выполняется свойство асимптотической коммутативности £ 1 ( t ) - £₂( t ) ^ 0 при t ^ да ;

• 2)    если ФП ограничена, то v = 0 , все КП (12) обладают общей асимптотой £ = Ф (о _n П ( да ) ) при t ^ да и £ 1 ( t ) - £₂( t ) ^ 0 для любых программ с одинаковыми о _n ;

• 3)    если о _n = 0 (для финитных программ нагружений (10) с полной разгрузкой), то при t >да асимптотика КП (12) имеет вид £( t ) = Ф ( vs + z ( t )) , z ( t ) ^ 0 , КП (12) обладает

горизонтальной асимптотой г = Ф ( vs ) , остаточная (пластическая) деформация £ _т = Ф ( vs ) не зависит от значений ФП на конечном интервале времени и отлична от нуля тогда и только тогда, когда vs ^ 0 ; если ФП обладает свойством v = 0 , то £ _т = 0 для любых ступенчатых программ нагружения (10).

Пункты 2 и 3 теоремы следуют из представления (15), а доказательство п. 1 приведено в работе [28].

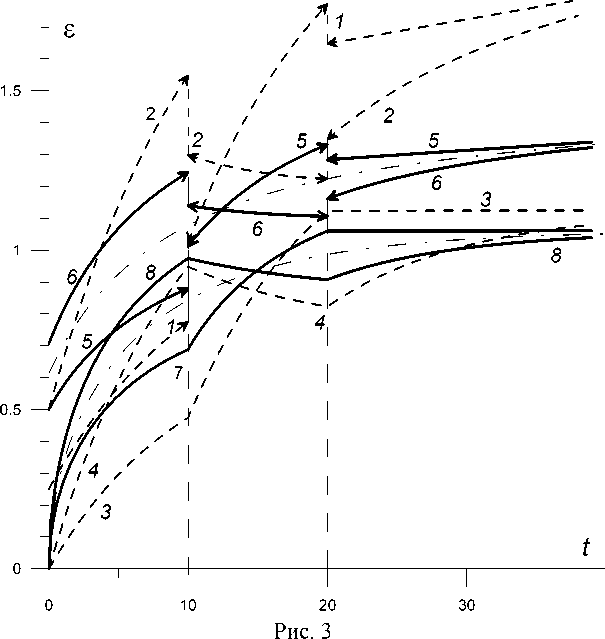
На рисунке 3 приведены КП (12) для трехступенчатых программ (10) с t 1 = 10 , t ₂ = 20 , о 1 = 0,5 , о₂ = 1 и о₃ = 0,5(о 1 + о₂) (КП 1, 3, 5, 7 ) и с перестановкой ступеней о 1 и о₂ (КП 2, 4, 6, 8 ) для двух линейных (штриховые линии 1 – 4 ) и двух нелинейных моделей: КП 1, 2 – для линейной РеМ-4 ( П = a t + в — Ye ~^ ) с а = 0,01 , в = 2 , Y = 1,5 , ^ = 0.1 ; КП 3, 4 — для линейной модели Фойгта с в = Y = 1,5 , ^ = 0,1 , а = 0 (с таким же временем ретардации т = 1/ X = 10 ); КП 5, 6 и 7, 8 - для двух нелинейных моделей (1), получающихся из РеМ-4 и модели Фойгта введением МФ Ф = x^0,5 . Штрих-пунктирные линии - КП (8) этих двух нелинейных моделей при постоянном напряжении о = 0,5(о 1 + о₂) (при о₂ >  O 1 для них справедливо неравенство е( t ;о₁,о₂) >  е( t ;о) >  s( t ,о₂,о 1 ) при всех t >  t ₂ ). Рисунок 3 иллюстрирует асимптотическую коммутативность КП при перестановке ступеней нагружения: для каждой из четырех моделей е( t ;о 1 ,о₂) — е( t ,о₂,о 1 ) ^ 0 при t ^да (п. 1 теоремы). ФП модели Фойгта (СиМ-2) ограничена и потому КП 3, 4, 7, 8 обладают горизонтальными асимптотами (п. 2 теоремы). В силу формулы (14) из П (0) = 0 следует, что КП 3, 4, 7, 8 непрерывны и в точках t = t_t , а у КП 1, 2, 5, 6 есть скачки (помечены стрелками на рис. 3), причем в случае линейной модели скачки при догрузке и разгрузке одинаковы по модулю.

Условия затухания памяти

Если для любой программы нагружения (10) отклонение (16) КП (12) от КП ε₀( t ) = Φ (σ _n Π ( t - t_{n - 1})) , соответствующей мгновенному нагружению от нуля до уровня σ _n в момент t_{n - 1} стремится к нулю при t → ∞ , будем говорить, что ОС обладает свойством затухающей памяти (о начальной истории) [33; 34; 40].

В случае линейного ОС (2) условие v = 0 на ФП необходимо и достаточно для затухания памяти (для Φ ( x ) = x (17) дает Δ ( t ) = z ( t ) → 0 при t → ∞ ). Если v >  0 (как, например, у параллельных соединений моделей Максвелла, то есть РеМ-2 n ), то след от прямоугольного импульса нагрузки не стирается никогда (остаточная деформация ε _∞ = σ vT ), а при несимметричном циклическом нагружении происходит неограниченное нарастание пластической деформации (ratcheting). Для нелинейного ОС (1) условие v = 0 не достаточно для затухания памяти: отклонение (17) не обязано стремиться к нулю, если Π ( ∞ ) ≠ ∞ . Чтобы обеспечить Δ ( t ) → 0 , надо наложить на Φ и Π дополнительные требования [28].

Теорема 2. Пусть выполнены предпосылки теоремы 1. Тогда для того, чтобы ОС (1) обладало свойством затухающей памяти при ползучести (то есть отклонение Δ ( t ) стремилось к нулю при t → ∞ для всех КП (12) при любых ступенчатых нагружениях (10)), необходимо, чтобы Π ( ∞ ) = 0 , и достаточно выполнения одного из двух следующих условий:

• 1)    ФП ограничена на [0; ∞ ) ( Π ( ∞ ) < ∞ ), а МФ Φ ( x ) – любая допустимая;

• 2)    v = 0 и существует число C >  0 такое, что Φ′ ( x ) ограничена сверху при | x | > C (то есть существует c >  0 : φ ′ ( u ) ограничена снизу при | u | >  c ).

Пункт 1 теоремы 2 следует из представления (16) для отклонения Δ ( t ) , так как из ограниченности ФП вытекает v = 0 и предельные равенства Φ (σ _n Π ( t - t_{n - 1})) → Φ (σ _n Π ( ∞ )) , Φ (σ n Π ( t - t n - 1 ) + vs + z ( t )) → Φ (σ _n Π ( ∞ )) и Δ ( t ) → 0 при t → ∞ , а доказательство п. 2 приведено в работе [28].

Замечание. Если v ≠ 0 и σ _n ≠ 0 , то возможны два случая: s = 0 (специально подобранные программы нагружения) и s ≠ 0 (основной). Если s = 0 , отклонение (16) будет стремиться к нулю лишь при дополнительных ограничениях на МФ Φ (достаточно требовать ограниченность Φ′ ( x ) ). Если же s ≠ 0 , то ограниченности Φ′ ( x ) не достаточно, и для обеспечения Δ ( t ) → 0 нужны гораздо более сильные ограничения на МФ. В отличие от линейного ОС (2), когда Φ ( x ) = x и Δ = ε( t ) - σ _n Π ( t - t_{n - 1}) = vs + o (1) , то есть Δ ( t ) → vs ≠ 0 и память не затухает при v ≠ 0 , для нелинейного ОС (1) возможны разные варианты поведения Δ ( t ) при t → ∞ в зависимости от свойств Φ . Если существуют пределы Φ′ ( +∞ ) и Φ′ ( -∞ ) производной Φ′ ( x ) при x → ±∞ и оба равны нулю (то есть φ ′ (ω _- + 0) = φ ′ (ω ₊ - 0) = +∞ ), а ФП не ограничена, то Δ ( t ) → 0 для любой программы нагружения (10) с σ _n ≠ 0 . Это выполнено, например, для МФ φ( u ) вида (6).

Модель может обладать затухающей памятью, хотя ни одно из достаточных условий теоремы 2 не выполнено. Примером может служить модель (1) с МФ

Π(t) =atu , a > 0, u ∈ (0;1); Φ(x) =A[ϑxm+(1-ϑ) x1/m], m > 1, A > 0 , ϑ ∈ (0;1] .   (18)

При любых значениях параметров a , u , m , Э , A в (18) необходимое условие v = 0 выполнено, а оба достаточных условия затухания памяти из теоремы 2 не выполняются: 1) П ( да ) = да при и <  1 ; 2) производная Ф' = Am Э х^{т 1} + m 1 (1—9) x ^{(1 m} )/ ^m ] не ограничена при m >  1 . В [28] доказано, что критерий затухания памяти для моделей (18) имеет вид 1 <  m <  1/ и . Если же m >  1/ и , то А ( t ) ^ да .

Накопление пластической деформации при циклическом нагружении

Для линейного ОС (2) условие v = 0 на ФП необходимо и достаточно для затухания памяти при ступенчатых нагружениях (п. 2 теоремы 2 выполняется). Если v >  0 (как, например, у модели Максвелла и всех РеМ-2 n ), то при несимметричном циклическом ступенчатом нагружении (с чередующимися напряжениями σ₁ , σ₂ , приложенными в течение времени τ , и произвольным временем отдыха между циклами нагружения) происходит неограниченное нарастание пластической деформации (рэтчетинг) со скоростью v т (о 1 + о₂) за цикл. Если же v = 0 , то полная деформация ограничена и стабилизируется, в этом случае ОС (2) моделирует приспособляемость материала (shakedown).

При периодическом ступенчатом нагружении с двумя ступенями равной длительности 0.5т в цикле ( t i _{+ 1} — t i = t 1 = 0.5 т , о₂ i _{+ 1} = о 1 , о₂ i = о₂ , i = 1,... ) на интервалах t е ( t i - 1 ; t i ) для кривой ползучести, порождаемой ОС (1), справедливы формулы (12), (15). Пластическая деформация за N циклов:

Pn = Ф( VsN ), sN = s = 0.5т(о1 + o2)N                    (19)

2 n

(так как s = ^ о i ( t i — t i - 1 ) , N = 2 n ). Если v = 0 , то p_N = 0 , то есть любое циклическое i = 1

нагружение не вызывает накопления пластических деформаций (ибо Ф (0) = 0 ).

Если v ^ 0 , несимметричное циклическое нагружение (с о₂ ^ — о 1 ) всегда вызывает монотонное нарастание модуля пластической деформации, а в случае о₂ = — о , будет p_N = 0 (так как s_N = 0 ), а КП - периодическая функция. В отличие от линейного ОС, скорость нарастания пластической деформации не постоянна. Приращение пластической деформации за j -й цикл выражается формулой

P j ^— P j — 1 = ^{Ф ( vs}j ) ^{— Ф ( vs}j — 1 ) .                                (20)

Если МФ ограничена, то моделируется приспособляемость, если нет – рэтчетинг , то есть неограниченное нарастание пластической деформации.

Из (19) следует, что для любых МФ прирост пластической деформации за фиксированное время А t не зависит от частоты (периода т) цикла нагружения с заданными амплитудами о 1 , о₂ : если N 1 T 1 = N ₂т₂ = A t , то

p (At) = Ф( vs (At)), s (At) = 0.5 (о1 + о2)А t

(рассматривается изотермический режим, то есть не учитывается разогрев материала при нагружениях с достаточно высокой частотой). Все сказанное справедливо и в случае, когда диссипативные свойства материала и скорости ползучести при растяжении и сжатии не одинаковы (Ф(х) не нечетна).

Кривые ползучести при двухступенчатом нагружении, обратная ползучесть

Для иллюстрации различия свойств КП (12), порождаемых линейным и нелинейным ОС, рассмотрим случай n = 2 . Тогда при t >  t 1 имеем:

е(t) = Ф(о1 П(t) + (о2 - о1 )П(t -t1)), или e(t) = Ф(о2П(t -t1) + o1 5(t; t1)), или e(t) = Ф(о2 П(t) + (o1 - o2) 5(t; t1)),       (21)

где 5 ( t ; t 1 ) = П ( t ) -П ( t - t 1 ) , t >  t 1 , - положительная убывающая функция аргумента t , 5 ( t ; t 1 ) ^ vt 1 >  0 при t ^да . Для КП (21) с о 1 >  0 всегда е( t ) >Ф (о₂ П ( t - t 1 )) , так как 5 ( t ; t 1 ) >  0 , а Ф ( х ) возрастает (в отличие от случая линейного ОС, отклонение А ( t ): = е( t ) - Ф (о₂ П ( t - 1 1 )) уже не обязательно убывает). Аналогично из второго представления (21) следует, что е( t ) > Ф (о₂ П ( t )) при о₂ <  о 1 и

Ф (о₂ П ( t - 1 1 )) <  е( t ) < Ф (о₂ П ( t )) при о₂ >  о 1 , t >  t 1 ,                 (22)

то есть при о₂ >  о 1 >  0 верна двусторонняя оценка для КП (21), не зависящая от о 1 .

Из (15) при n = 2 следует, что при t ^ да КП (21) имеет асимптотику

е( t ) = Ф (о₂ П ( t - 1 1 ) + о 1 vt 1 + o (1)) , или е( t ) = Ф (о₂ П ( t ) + (о 1 - о₂) vt 1 + о (1)) .

Если ФП ограничена, то v = 0 и е( да ) = Ф (о₂ П ( да )) , то есть КП (21) стремится к горизонтальной асимптоте. Если обе МФ не ограничены (и о₂ Ф 0 ), то е( t ) ^ да .

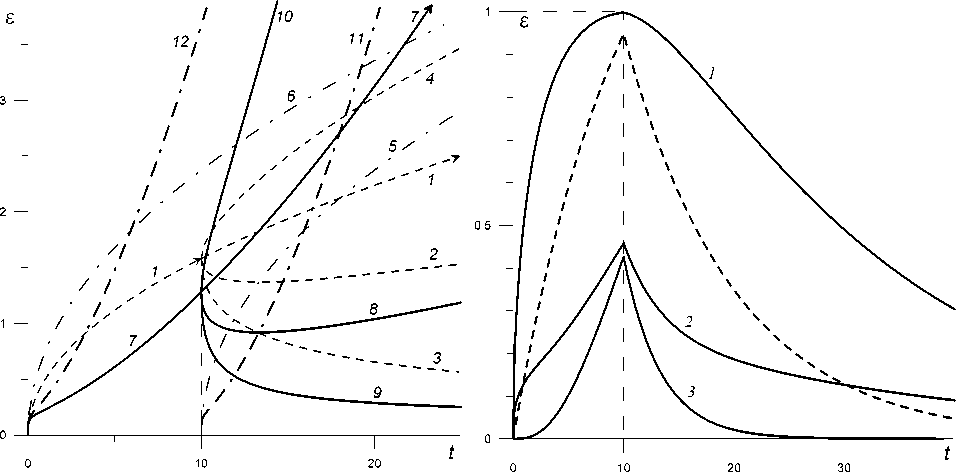
Рис. 4

Рис. 5

На рисунке 4 приведены КП (21) фрактальной линейной модели с ФП П = At" , A = 0,5, и = 0,5 для программ нагружения с t₁ = 10 , о 1 = 1 и а₂ = 1; 0,5; 0; 1,5 (штриховые кривые 1-4 ) и КП нелинейной модели с МФ Ф( X) = 0,25( х + х¹³') (вида (18) с m = 3 , 3 = 0,5 , A = 0,5 ) и той же ФП для тех же программ нагружения (кривые 7-10 ). Так как П (0) = 0 , то в т. t = t 1 все КП 1-4 и 7-10 не имеют разрыва; из П (0) = +» следует, что у всех КП П ( t 1 + 0) = ±да (знак совпадает с sgn(o₂ — С 1 ) ). Штрих-пунктирные линии 11, 12 - обычная КП е = Ф (о₂ П ( t )) и ее сдвиг е = Ф (о₂ П ( t — t j )) с о₂ = 1,5, участвующие в оценке (22) для КП (21) с о₂ = 1,5; линии 5, 6 - аналогичные оценки для КП линейной модели. Для любого и <  1 , очевидно, v = 0 , и потому о₂( П ( t ) — П ( t — t 1 )) ^ 0 и е( t ) — о₂ П ( t ) ^ 0 при t ^да (см. теорему 2). Таким образом, ширина полосы между кривыми 5, 6 стремится к нулю, и эта линейная модель (класса НеМ) обладает свойством затухания памяти. Однако нелинейная модель им не обладает, так как введение МФ Ф ( х ) вида (18) меняет ситуацию: при заданных значениях и = 0,5 , m = 3 не выполняется критерий затухания памяти 1 <  m <  1/ и для моделей семейства (18). Их КП (21) не сходятся к обычной КП и отклонение А ( t ) стремится к бесконечности при t ^ да , а полоса между кривыми 5, 6 не стягивается к нулю, а неограниченно расширяется. Отметим, что при любом о₂ е (0; о 1 ) у КП есть точка минимума t m >  t 1 (см. кривые 2, 8 ), она двигается вправо от t 1 до да с убыванием о₂ от G , до нуля (см. кривые обратной ползучести 3, 9 ), так как функция t m (о₂) убывает, t m (0 + ) =да , t m ( а , — 0) = t 1 [28]. Наличие точек экстремума деформации между точками разрыва программы нагружения наблюдается в испытаниях разных материалов [3; 6; 47; 50; 57], но, как правило, считается признаком нелинейности их поведения.

При о₂ = 0 формула (21) дает уравнение кривой обратной ползучести (КОП):

е(t,а,t1) = Ф(оП(t)) при t < t1; е(t;а, t1) = Ф(оS(t;t1)) при t > t1,          (23)

где S ( t ; t 1 ) =П ( t ) — П ( t — 1 1 ) , g: = о 1 >  0 . Уравнение (23) справедливо при условии о П ( t ) е D ф для t <  t 1 , то есть о П ( t 1 ) <  х . Тогда КОП (23) определена на всем луче t >  0 , так как S ( t ; t ₁ ) убывает по t в силу выпуклости вверх ФП [57].

Семейство КОП (23) возрастает по о при любом t >  0 . Для любого (допустимого) о >  0 КОП (23) возрастает по t на всем промежутке t <  t 1 , и убывает (нестрого) на луче t >  t 1 (у вязкого элемента и модели Максвелла е( t ;о, t 1 ) = Ф (оа t 1 ) = const >  0 при t >  t 1 , а у упругого элемента е( t ) = 0 ). Так как при t > да П ( t ) — П ( t — 1 1 ) ^ vt 1 , где v : = П ( да ) >  0 [57], то КОП (23) стремится к пределу е _да =Ф (а vt 1 ) ; е _да имеет смысл остаточной деформации (при бесконечно долгой выдержке). Как и для линейного ОС (2), е _да = 0 только тогда, когда v = 0 (в силу возрастания МФ Ф ( х ) и требования Ф (0) = 0 ); лишь в этом случае моделируется «полное восстановление». При v ^ 0 знаки е _да и о совпадают.

Ограничение П ( t ) <  0 , выведенное для линейного ОС (2) [57], и возрастание МФ ф обеспечивают монотонное убывание КОП (23) при t >  t ₁ , никакие дополнительные ограничения на ф для этого не требуются . Возрастание П ( t ) гарантирует выпуклость вниз на луче t >  t ₁ КОП линейного ОС е( t ) = о S ( t ; t ₁) , 5 >  0 , но для выпуклости вниз КОП (23) этого уже не достаточно.

Качественные отличия КОП ОС (1) от КОП линейного ОС (2), обусловленные введением второй МФ: 1) КОП (23) с 5 >  0 уже не обязана быть выпуклой вверх на интервале (0; t ₁) и выпуклой вниз на луче t >  t ₁ и может иметь точки перегиба; 2) у линейного ОС скачки в т. t = t ₁ деформации и скорости е( t ₁) = - 5 П (0) = - е(0) и е ( t ₁) = - 5 П (0) = - е(0) не зависят от t ₁ , а у нелинейных регулярных моделей скачки

е( t1) = Ф(5 П( t1) - 5 П(0))-Ф(5 П( tj) < 0, (24) е( t1) = о[П (t1)-П (0)] Ф'(о[ П( t1)- П(0)]) - о П (^)Ф'(о П( tj) < 0

зависят от t ₁ и не равны по модулю скачкам е(0) и е(0) в момент нагружения t = 0 (наличие этих свойств у экспериментальной КОП – индикаторы неприменимости линейного ОС).

На рисунке 5 приведены КОП (23) (с 5 = 1 , t ₁ = 10 ) для моделей с П ( t ) = в - в e " (ФП модели Фойгта) с в = 1,5 , ^ = 0,1 и четырех разных МФ: штриховая кривая - для Ф ( x ) = x (КОП линейной модели Фойгта), кривая 1 - для Ф ( x ) = [1 - ( x - 1) ² ] ^0,5 , x g [0;1] ; 2 - Ф( x ) = 0,25( x ³ + x ^V3) ( Ф ( x ) вида (18) с m = 3 , 9 = 0,5 , A = 0,5 ); 3 - для Ф ( x ) = 0,5 x ³ . Разрыва в т. t = t ₁ нет, так как П (0) = 0 (см. (24)). Формы КОП 1-3 качественно отличаются от типичной КОП, порождаемой линейным ОС.

Заключение

Аналитически изучены и сопоставлены общие свойства и качественные особенности кривых ползучести (12), порождаемых линейным ОС вязкоупругости (2) и обобщающим его нелинейным определяющим соотношением Работнова (1) при произвольных ступенчатых нагружениях (10), исследованы их зависимость от характеристик двух материальных функций (МФ) и параметров программы нагружения. Получены формулы для скачков деформации в точках разрыва напряжения, для остаточной деформации при полной разгрузке и для отклонения от обычной кривой ползучести (с нулевой предысторией); исследованы асимптотика кривых ползучести (12) в бесконечности, влияние перестановки ступеней нагружения, скорость рэтчетинга при циклическом нагружении, условия монотонности кривой обратной ползучести. Доказано, что ОС (1) с любыми (допустимыми) материальными функциями обладает свойством асимптотической коммутативности при перестановке ступеней нагружения, а остаточная деформация не меняется (теорема 1). Установлены достаточные условия затухания памяти ОС при ступенчатых нагружениях (теорема 2).

В результате сравнения обнаруженных свойств теоретических кривых ползучести (12), порождаемых линейным ОС вязкоупругости (2) и нелинейным ОС Работнова (1), друг с другом и с типичными свойствами экспериментальных кривых ползучести вязкоупругопластичных материалов сопоставлены арсеналы возможностей ОС (1) и (2) по описанию различных эффектов при ползучести, выявлены дополнительные возможности ОС (1) и свойства, унаследованные им от линейного соотношения вязкоупругости. Установлено, что зависимость (14) скачков КП от параметров программы нагружения и ФП Π (t) отличается от линейного случая не только нелинейностью, но и нелокальностью, в частности, модуль скачка деформации (14) зависит не только от модуля скачка напряжения (как у линейного ОС), но и от его знака, от истории нагружения и накопленной деформации ползучести. Поэтому нелинейное ОС (1) способно (в отличие от линейного ОС) описывать явление дрейфа мгновенно-упругой деформации вследствие ползучести.

МФ φ( u ) в ОС (1) также меняет асимптотику (15) кривых ползучести в бесконечности и скорость рэтчетинга при циклических нагружениях (20), оно порождает более сложные условия затухания памяти (теорема 2) и ограниченности деформации при циклических нагружениях, чем у линейного ОС. Показано, что равенство нулю величины предела v = Π ( ∞ ) производной функции ползучести в бесконечности – критерий полного восстановления после снятия нагрузки, необходимое условие затухания памяти (но не достаточное, в отличие от линейной вязкоупругости) и критерий отсутствия накопления пластической деформации при циклических нагружениях. Если v ≠ 0 , несимметричное циклическое нагружение всегда вызывает монотонное нарастание модуля пластической деформации. В отличие от линейного ОС, скорость нарастания пластической деформации за цикл (20) не постоянна. Если МФ ограничена, то моделируется приспособляемость, если нет – рэтчетинг.